XXXIII. Приложения геометрии Лобачевского к теории автоморфных функций
|
Как мы знаем, приложения неевклидовой геометрии к другим отделам математики Лобачевский видел в ее применении к вычислению определенных интегралов. После того как неевклидова геометрия получила признание и сосредоточила на себе внимание многих выдающихся математиков, ее приложения к другим отделам математики очень расширились. Мы не имеем возможности здесь подробно их излагать; но нельзя не остановиться на роли геометрии Лобачевского в создании целой дисциплины большого значения — теории автоморфных функций. Это учение было построено Пуанкаре, главным образом, в промежутке между 1881 и 1884 гг., после чего получило большое развитие в трудах как самого Пуанкаре, так и многих других авторов1. Настоящий очерк имеет в виду выяснить основные задачи этой теории и роль геометрии Лобачевского при их разрешении в изложении, доступном читателю, обладающему основами математического образования.
Тригонометрические функции sin а; и cos х, как известно, по началу определяются чисто геометрически для действительных значений аргументов. Так как, однако, они выражаются рядами, сходящимися для любого комплексного значения аргумента, то этими рядами их определяют для любого значения z = х + yi. Чтобы ближе держаться Лобачевского, заметим, что он в своей «Алгебре» определяет эти функции формулами Эйлера (в некоторой их модификации): 
Поскольку функции ezi и e-zi выражаются степенными рядами, сходящимися на всей числовой плоскости, этими формулами тригонометрические функции определены для любого комплексного значения z = х + yi. Основные соотношения между тригонометрическими функциями остаются в силе, каковы бы ни были значения аргумента. В частности, при любом целом k sin(z+2kπ) — sinz, cos(z+kπ)=cosz (II) для каждого значения z в комплексной плоскости; sin z и cos z суть периодические функции, с наименьшим периодом 2π. Иначе говоря, если подвергнуть независимую переменную z преобразованию z' = z+2kπ, (III) то функция сохранит свое значение: sinz' =sinz. Функция остается инвариантной при преобразовании (III) с любым целым значением k. Совокупность преобразований (III), соответствующих всевозможным целым значениям параметра k, явно образует группу, так как из z' = z+2kπ и z" 2k'π следует z" = z + 2(k+k')π. Однако это группа разрывная или дискретная в том смысле, что при целых значениях к одно преобразование не переходит в другое непрерывным изменением этого параметра,— значения его переходят одно в другое скачками. Эта периодичность получает простое геометрическое выражение. Если в числовой плоскости провести прямые, параллельные мнимой оси на расстоянии одна от другой (рис. 51), то в пределах полосы функции sin z и cos z принимают все доступные им значения, и притом внутри полосы каждое один раз; только на границах полосы значения функции повторяются. Эти полосы называются фундаментальными областями функции. Исследование функции таким образом сводится к изучению ее значений внутри фундаментальной области. По существу, дело обстоит так же и в отношении эллиптических функций. Эти последние, как известно, имеют два независимых периода ω1 и ω2. Каждая эллиптическая функция остается инвариантной при преобразованиях z' = z+k1ω1+k2ω2 (IV) с целыми коэффициентами k1, k2,. Фундаментальными областями для этих функций служат конгруэнтные параллелограммы, на которые разбивается числовая плоскость. 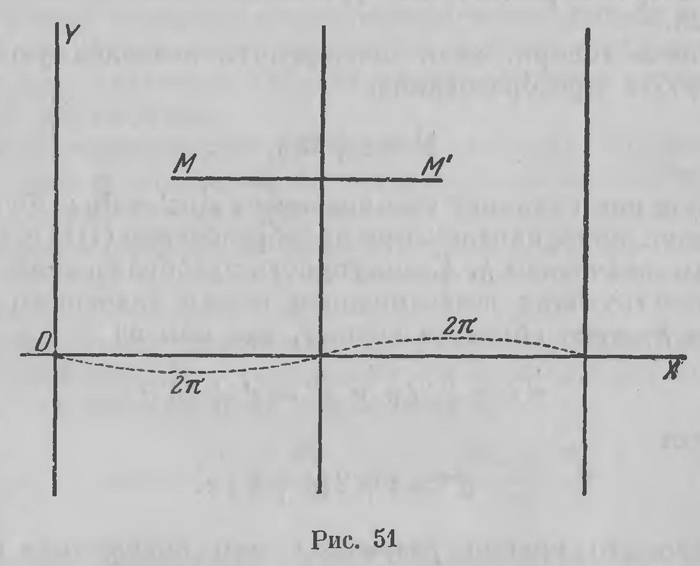
Преобразования (IV) также составляют дискретную группу — «группу автоморфизмов эллиптической функции», т. е. тех преобразований, при которых функция сохраняет свое значение — остается инвариантной. Исследование функции требует ее изучения внутри фундаментальной области. Пуанкаре поставил задачу о разыскании и исследовании тех функций, которые остаются инвариантными при некоторых преобразованиях вида частными случаями их являются преобразования (III) и (IV). 
Это должна быть разрывная группа, потому что функция, остающаяся инвариантной при всех преобразованиях непрерывной группы, неизбежно сводится к постоянной, функции комплексной переменной z, удовлетворяющие этим требованиям, т. е. остающиеся инвариантными при некоторой разрывной (дискретной) группе дробно линейных преобразований (V), в настоящее время называют автоморфными функциями. Задачу об исследовании автоморфных функций впервые поставил Пуанкаре, хотя он и сам указывает, что в отношении некоторых функций этого рода он имел предшественников. Самое исследование он проводит в следующем порядке. Во-первых, он старается установить, каковы могут быть фундаментальные области автоморфной функции; во-вторых, владея уже разбиением плоскости на фундаментальные области, он ставит себе задачей разыскать те преобразования, которые замещают эти области Друг другом, так сказать, перетасовывают их; в-третьих, зная фундаментальные области, он разыскивает и соответствующие функции. Из этих задач основной является разыскание возможных фундаментальных областей. Чтобы уяснить себе, как разрешается эта первая задача, мы остановимся на простейшем частном случае, по которому читатель вполне уяснит себе роль неевклидовой геометрии в этом вопросе. Прежде всего заметим, что преобразования комплексной переменной (V) всегда переводят окружности в окружности же; это — круговые преобразования; при этом прямые, как обыкновенно, включаются в число окружностей. Доказательство этого предложения можно найти в любом элементарном курсе теории функций комплексной переменной. Второе основное свойство этих преобразований, как осуществляемых аналитическими функциями комплексной переменной, заключается в том, что они конформны, т. е. сохраняют углы между любыми преобразуемыми линиями. Отметим далее, что в преобразовании (V) определись ad — Ьс должен быть отличен от нуля, так как в противном случае правая часть сводилась бы к постоянной. Если этот определитель отличен от единицы, то его можно привести к единице умножением всех коэффициентов на одно и то же число (действительное или мнимое). Дробно линейное преобразование (V), определитель которого равен единице, так что ad — Ьс = 1, (VI) в настоящее время обыкновенно называют гомографией. Пуанкаре начинает исследование с тех гомографии, коэффициентами которых служат действительные числа; их совокупность явно образует группу. Пуанкаре, может быть без достаточных оснований, называет ее фуксовой группой. Это название за ней в литературе утвердилось. Основное свойство преобразований этой группы заключается в том, что при них действительные значения z переходят в действительные же значения z'; можно показать, что этим свойством преобразования такой группы вполне определяются. Геометрически это означает, что при фуксовых преобразованиях ось действительных чисел переходит в себя самое. Но более того, можно без труда обнаружить, что верхняя полуплоскость (у > 0) при этих преобразованиях всегда переходит в себя самоё и нижняя полуплоскость (у < 0) также переходит в себя самое. Это и привело Пуанкаре к простейшей его интерпретации гиперболической геометрии, которая строится следующим образом. Примем за субстрат геометрии, которую будем строить, полуплоскость, лежащую над осью действительных чисел (у > 0) (рис. 52). За движения в ней примем преобразования фуксовой группы. Они зависят от трех параметров (от коэффициентов а, Ь, с, d, связанных уравнением (VI)). Говорят, что эти движения имеют три степени свободы. За "прямые" принимаем полуокружности, пересекающие действительную ось ортогонально, т. е. имеющие центр на действительной оси; к ним присоединяются полупрямые, перпендикулярные к оси. Эти "прямые" явно образуют гиперболическую связку (стр. 425), основная окружность которой вырождена в прямую (в действительную ось). Ясно, что через две "точки"2. А и В всегда проходит а и Только одна "прямая" (тот же рисунок). Располагая группой движений, легко уже построить метрику этого двумерного пространства как совокупность численных инвариантов группы движений. Действительная ось при атом оказывается геометрическим местом бесконечно удаленных точек плоскости (как всегда основная окружность гиперболической связки). 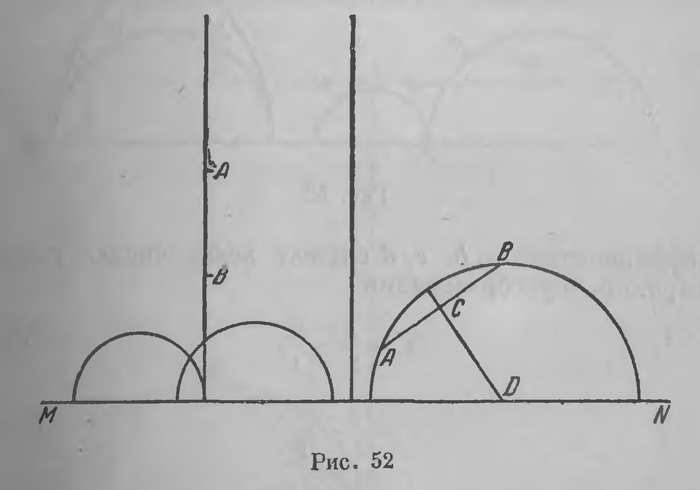
Две „прямые“, имеющие общую бесконечно удаленную "точку" (т. е. окружности, касающиеся одна другой на действительной оси, рис. 53), следует рассматривать как параллельные "прямые". Через точку Р, лежащую в плоскости вне "прямой" MN, проходят две параллельные ей "прямые" (рис. 53). Немного остается к этому прибавить, чтобы видеть, что мы имеем здесь интерпретацию геометрии Лобачевского в гиперболической связке с основной окружностью, выродившейся в действительную ось. Это — простейшая интерпретация по схеме Пуанкаре. Возвратимся теперь к автоморфным функциям. Рассмотрим простейшую разрывную подгруппу, входящую в состав общей группы фуксовых преобразований. Таковой является группа гомографий (V) и (VI), в которых 
коэффициентами а, Ь, с, d служат целые числа. Таковы, например, преобразования 
Эту подгруппу обыкновенно называют арифметической группой. Предполагая, что существуют автоморфные функции, для которых она служит группой автоморфизмов (т. е. которые остаются инвариантными при преобразованиях этой группы), разыщем соответствующие им фундаментальные области. С этой целью заметим, что в состав арифметической группы входят целые преобразования z' = z+m, (VIII) где m — любое целое число,— в частности, простейшее преобразование z'=z+1. Преобразования этой группы, как мы знаем, должны перетасовывать фундаментальные об ласти соответствующей автоморфной функции между собой. Если поэтому в комплексной плоскости проведем ряд прямых OU, AU, BU, параллельных мнимой оси (имеющих поэтому общую бесконечно удаленную точку U) и отстоящих одна от другой на расстояния, равные единице (рис. 54), то преобразование z'=z+1 будет замещать первую из этих полос смежною ей; значения автоморфной функции, соответствующей арифметической группе, повторяются в каждой полосе. 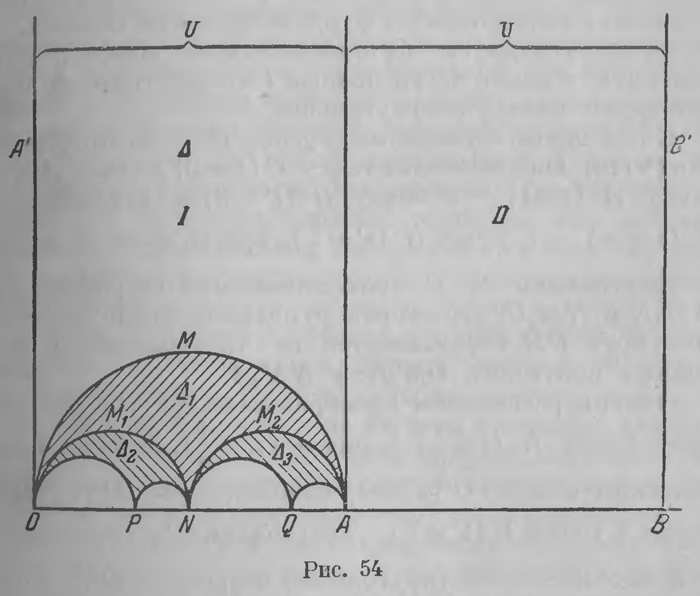
Заметим, что преобразования (VIII) сами образуют простейшую разрывную группу, входящую в состав общей арифметической группы. Для некоторых функций этой группы полосы на рис. 54 суть Фундаментальные области; таковы, например, функции sin2πz и cos2πz. Но в отношении автоморфных функций, соответствующих всей арифметической группе, эти полосы не представляют фундаментальных областей; другими преобразованиями этой группы они разбиваются на части — фундаментальные области всей арифметической группы. Постараемся эти области выявить. На отрезке О А как на диаметре (рис. 54) опишем полуокружность ОМА. Она разобьет полосу на криволинейный треугольник OUА (со сторонами OU, UA и АМО) и полукруг ОМ АО. Исследование обнаруживает, что преобразования арифметической группы, оставляющие действительную ось инвариантной, не разбивают треугольника на части, он представляет фундаментальную область. Чтобы разыскать другие фундаментальные области, нужно выяснить, в какие части полосы I арифметические преобразования приводят треугольник А. С этой целью остановимся прежде всего на преобразовании (VIIa). Оно приводит точку О (z = 0) в точку A(z' =1), точку A (z =1)—в точку О (z' = 0) и, наконец, точку U (z = ∞) —в точку N (z'=1/2). Треугольник Δ перейдет в треугольник Δ1 с криволинейными сторонами ОМА, AM2N и NM1O'; это вторая фундаментальная область Δ1. Полукруг ОМА разбивается на треугольник Δ1 и два равных полукруга OM1N и NM2A. Теперь рассмотрим преобразование (VIIb). Оно оставляет точку N (z = 1/2) в покое (z'=1/2), точку A (z = 1) приводит в точку О (z'= 0), наконец, точку О (z=0) приводит в точку Р (z' =1/2). Треугольник Δ1 переходит в Δ2 с криволинейными (круговыми) сторонами ON, NP, РО. Из полукруга OM1N выделяется вторая фундаментальная область Δ2 и два полукруга. Аналогично преобразование (VIIe) также оставляет точку N (z = 1/2) в покое, приводит точку О (z =0) в точку А (z'= 1), точку A (z=1)—в точку Q (z' = 2/3). Из полукруга NM2A выделяется новая фундаментальная область— (криволинейный) треугольник Δ3 и два полукруга. Таким образом, ужо выделены четыре фундаментальные области в виде треугольников, составленных полуокружностями, ортогональными к действительной оси, и четыре полукруга. При дальнейшем исследовании обнаруживается, что каждый из оставшихся кругов вновь разбивается на фундаментальный (криволинейный) треугольник и два новых полукруга. Образующиеся полукруги быстро убывают, и выделенные фундаментальные области постепенно захватывают все точки полосы. Это странное строение фундаментальных областей, постепенное и притом очень быстрое убывание их размеров по мере приближения к действительной оси естественно вызвало у Пуанкаре желание выяснить закон строения и расположения этих областей, который проливал бы свет на их структуру для любой автоморфной функции. Решение долго не давалось. Но внезапно, совершенно неожиданно у Пуанкаре выплыло сознание, что разгадка коренится в неевклидовой интерпретации всей картины. Вот как сам Пуанкаре описывает этот любопытный эпизод3. «Это было в момент, когда я покидал город Канн, где я тогда жил, чтобы принять участие в геологической экскурсии, организованной Горной школой. В перипетиях путешествия я позабыл о своих математических работах. По прибытии в Кутанс мы сели в омнибус для прогулки. В момент, когда я ставил ногу на подножку, мне пришла идея, совершенно не подготовленная моими предыдущими размышлениями,— что преобразования, которыми я пользовался для определения фуксовых функций, совпадают с движениями в неевклидовой геометрии. Возвратившись в Канн, я проверил результат, который оказался совершенно правильным». Идея, которая осенила Пуанкаре, была та интерпретация геометрии Лобачевского, которая носит его имя, в частности, простейшая ее форма, изложенная выше, изображенная на рис. 52. Верхняя полуплоскость отображает гиперболическую плоскость, точки действительной оси — бесконечно удаленные ее точки. Мы можем смотреть и так, что гиперболическая плоскость представляет собой отображение этой евклидовой полуплоскости. Если мы сообразно этому отобразим конфигурацию фундаментальных областей, изображенную на рис. 54, на гиперболической плоскости, то каждая область будет представлена треугольником, все три вершины которого лежат в бесконечности. 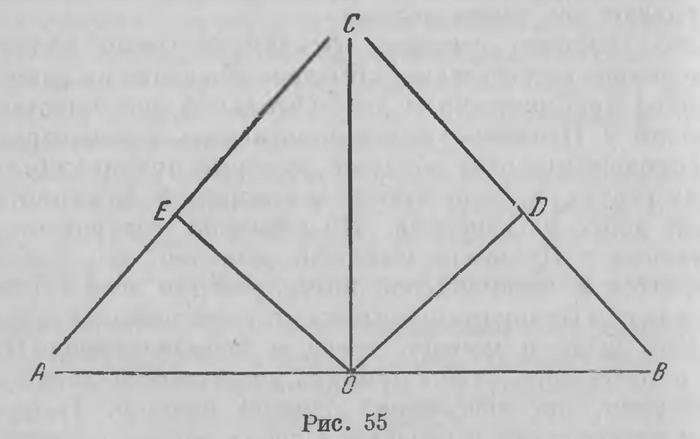
Это так называемый вполне вырожденный треугольник. Такой треугольник в гиперболической плоскости строится очень просто. Возьмем два смежных прямых угла АОС и ВОС (рис. 55), разделим их пополам и на биссектрисах отложим отрезки OD и ОЕ — отрезки параллельности, соответствующие углу 45°. Если через точки D и Е проведем прямые ВС и АС, перпендикулярные к биссектрисам, они будут параллельны сторонам прямого угла, будут параллельны между собой и вместе с прямой АВ образуют такой вырожденный треугольник ABC, все вершины которого лежат в бесконечности. Все такие вполне вырожденные треугольники конгруэнтны между собой. Теперь ясно, что конфигурация рис. 54 на гиперболической плоскости представляет ее разложение на конгруэнтные вырожденные треугольники Δ, Δ1, Δ2 —представляющие фундаментальные области Нрпфметической группы. Загадка разрешена. Но более того, развитие ее приводит к общему решению задачи о форме фундаментальной области, соответствующей любой автоморфной функции. Такой фундаментальной областью при отображении на гиперболическую плоскость всегда служит прямолинейный многоугольник. За исключением простейшего случая, который мы рассмотрели выше, когда фундаментальными областями служат треугольники, во всех других случаях фундаментальные области, будучи отображены на гиперболической плоскости, представляют собой многоугольники с четным числом сторон. Противоположные стороны такого многоугольника всегда конгруэнтны между собой. Эти многоугольники, обладают и некоторыми другими особенностями, перечислять которые здесь вряд ли уместно. Существенно лишь то, что вся задача о разыскании фундаментальных областей автоморфных функций сводится к нахождению конгруэнтных многоугольников определенного типа, на которые может быть разбита всякая гиперболическая плоскость. Эта основная идея — применения геометрии Лобачевского — послужила для Пуанкаре точкой отправления при построении всей теории автоморфных функций. Почти во всех мемуарах Пуанкаре говорит, что геометрия Лобачевского служила ему в этих исследованиях руководящею нитью. Однако он прибавляет, что избегает в своем изложении пользоваться неевклидовой геометрией, так как с нею математики недостаточно знакомы. Это было около семидесяти лет тому назад, когда неевклидова геометрия, еще недавно признанная, действительно была мало известна. В настоящее время теория автоморфных функций всегда излагается на базе геометрии Лобачевского. 1Основной мемуар Пуанкаре «Theorie des groupes fuchsiens» помешен в I томе журнала «Acta Mathematical). Все его работы по теории автоморфных функций сосредоточены во II томе собрания его сочинений: «Oeuvres de Henri Ротсагё», t. II. Из обширного ряда сочинений других авторов по этой дисциплине укажем два наиболее обстоятельных сочинения: R. Friсkе und F. Klein. Vorlesuiigen uber die Theorie der automorphen Funktionen. Leipzig und Berlin, 1926; P. Fatоu. Fonctions automorplies во втором томе трактата Аппеля и Гурса — Р. Арреl et Е. Gоursat, Theorie des fonctions algebriques d’une variable et des transcend antes qui s’y rattachent. Paris, 1930. На русском языке имеется переводное сочинение Л. Форд, Теория автоморфных функций. М. — Л., 1936. 2Термины, относящиеся к геометрии связки, взяты в кавычки. 3Н. Роinсаre. Science et Methorio. Paris, 1908. Есть русский перевод: Г. Пуанкаре. «Наука и метод». С.-Петербург, 1910 |
загрузка...
