XXIX. Предыстория неевклидовой геометрии

Приведенное письмо Гаусса имело и другое значение. Из него было видно, что Гаусс уже давно, с 1792 г., в некоторой мере владел теми идеями, которые в углубленном развитии были опубликованы Лобачевским. Из того же письма видно, что к этим идеям приходили и другие геометры, в частности Швейкарт, который назвал неевклидову геометрию «звездной». Еще более подробные сведения об этом оказались в письмах к Шумахеру от 1831 г., а по опзтбликовании переписки Гаусса с другими друзьями, Ольберсом, Бесселем и В. Больаи, стало ясно, что неевклидова геометрия, опубликованная впервые Лобачевским, имела свою предысторию, носившую своеобразный, эпизодический характер. Отдельные эпизоды этой истории частью были ранее скрыты от математического мира и вскрылись только в этой переписке, частью получили и некоторое выражение в брошюрах, которые в свое время совершенно ускользнули от внимания математиков. Эта история несомненно имеет большой интерес; она послужила предметом обстоятельного исследования и теперь полностью выяснена, главным образом благодаря трудам двух германских ученых — Ф. Энгеля и П. Штеккеля. Относящиеся сюда материалы опубликованы ими в очень интересной книге «Собрание первоисточников по предыстории неевклидовой геометрии»¹. Кроме того, Штеккель выпустил специальную книгу о геометрических работах Гаусса²; все материалы, относящиеся к Гауссу, опубликованы также в VIII томе полного собрания сочинений Гаусса³. Мы не можем не уделить здесь места краткому изложению этой предыстории неевклидовой геометрии.

В приведенном выше письме Гаусса к Шумахеру (от 28 ноября 1846 г.) он утверждает, что еще в 1792 г. пришел к тем взглядам, которые опубликованы в брошюре Лобачевского. Как далеко он в ту пору продвинулся по этому новому пути, сказать очень трудно, но в письме от 16 декабря 1799 г. к своему другу В. Больаи, приславшему на его усмотрение опыт доказательства постулата о параллельных линиях, Гаусс дает уже очень отчетливый очерк этих своеобразных идей. В этом его изложении нет еще речи о новой геометрии, но два обстоятельства выражены совершенно отчетливо. Во-первых, ясно, что Гаусс довольно далеко провел выводы, которые можно получить, отвергая постулат о параллельных линиях с целью его доказательства от противного; во-вторых, он пришел к сознанию, что эти выводы, быть может, вовсе не так несообразны, как это кажется на первый взгляд. И все же это были еще, так сказать, блуждания мысли, не вылившейся в определенные взгляды; твердо на этой точке зрения Гаусс еще не стоял; ближайшие годы принесли сомнения и колебания, которые отчетливо выражены в письме к тому же В. Больаи от 25 ноября 1804 г. Из этого письма совершенно ясно, что в конце 1804 г. Гаусс не считал еще попытку доказать постулат о параллельных линиях совершенно безнадежной. В продолжение ряда лет те же сомнения проскальзывают также в письмах и заметках, относящихся к 1808, 1808 и, наконец, к 1812 гг. В 1818 г. Хр. Герлинг, бывший ученик и друг Гаусса, получил поручение переработать учебник математики Лоренца (см. стр. 122). Герлинг встречает препятствия в изложении учения о параллельных линиях. Так как он уже раньше имел об этом переписку с Гауссом, то теперь обращается к нему за советом по этому вопросу. Он пишет Гауссу следующее (2 июля 1818 г.): «Я считаю правильным, что излагать это, т. е. учение о параллельных линиях, нужно по методу Евклида, однако указывая его недостаточность. Но как это сделать, мне не ясно. Я считаю, что было бы лучше всего привести в качестве аксиомы предложение: «через точку вне прямой можно провести к ней только одну параллельную ей прямую линию»⁴; в примечании же нужно указать, что доказательство этого предложения до сих пор найти не удалось, поэтому необходимо принять это предложение за аксиому, пока кто-либо не найдет его доказательства или не обнаружится его неправильность». Герлинг, таким образом, уже не исключал возможности, что постулат о параллельных может оказаться несправедливым; это несомненно было навеяно предыдущими беседами с Гауссом. В ответном письме (от 25 сентября 1818 г.) Гаусс по этому поводу замечает:

«Я очень рад, что Вы имеете мужество высказаться так, как будто Вы признаете возможным, что наша теория параллельных линий, а следовательно, и вся наша геометрия ложны. Но осы, гнездо которых Вы разрушаете, подымутся над Вашей головой».

Во всяком случае в письме от 8 ноября 1824 г. к молодому правоведу и математику Ф. Тауринусу, о котором еще будет речь, изложены основы геометрии, к которой приводит отрицание постулата Евклида, с определенностью, не оставляющей сомнения в том, что Гаусс в то время уже владел основными идеями геометрической системы, которую он назвал «неевклидовой геометрией». Приводим выдержку из этого письма:

«Допущение, что сумма трех углов треугольника меньше 180°, приводит к своеобразной, совершенно отличной от нашей (евклидовой) геометрии; эта геометрия совершенно последовательна, и я развил ее для себя (fur mich selbst) совершенно удовлетворительно; я имею возможность решить в этой геометрии любую задачу, за исключением определения некоторой постоянной, значение которой a priori установлено быть не может. Чем большее значение мы придаем этой постоянной, тем ближе мы подойдем к евклидовой геометрии, а бесконечно большое ее значение приводит обе системы к совпадению. Предложения этой геометрии отчасти кажутся парадоксальными и непривычному человеку даже несуразными; но при строгом и спокойном размышлении оказывается, что они не содержат ничего невозможного. Так, например, все три угла треугольника можно сделать сколь угодно малыми, если только взять достаточно большие стороны; площадь же треугольника не может превысить, даже не может достичь некоторого предела, как бы велики ни были его стороны. Все мои старания найти в этой неевклидовой геомтетрии противоречие или непоследовательность остались бесплодными, и единственно, что в этой системе противится нашему разуму, это то, что в пространстве, если бы эта система была справедлива, должна была бы существовать некоторая сама по себе определенная (хотя нам и неизвестная) линейная величина. Но мне кажется, что мы, кроме ничего не выражающей словесной мудрости метафизиков, знаем очень мало или даже ничего не знаем о сущности пространства; мы не можем смешивать того, что нам представляется неестественным, с абсолютно невозможным. Если бы неевклидова геометрия была истинной и упомянутая выше постоянная находилась в определенном отношении к таким величинам, которые доступны нашему измерению на небе или на земле, то ее можно было бы определить a posteriori. Я поэтому иногда в шутку высказывал желание, чтобы евклидова геометрия не была истинной, потому что мы тогда имели бы a priori абсолютную меру длины».

Читатель, который знаком уже с работами Лобачевского, видит, что это первые шаги в том построении, которое выполнено Лобачевским, начальные его предложения.

Письмо к Тауринусу, которое мы цитировали, заканчивается следующими словами:

«Относительно человека, который обнаружил глубокий математический ум, я не опасаюсь, что он дурно поймет изложенное выше; но во всяком случае вы должны смотреть на это, как на частное сообщение, которое отнюдь не должно быть опубликовано».

Эти строки очень характерны: Гаусс не только не публикует ничего о своих воззрениях на основы геометрии, но требует от всех тех, кого он посвящает в свои сокровенные мысли по этому вопросу, хранить их в самой строгой тайне. Каковы были причины этой сдержанности? Штеккель полагает, что причины эти были различны. Гаусс вообще склонен был публиковать результаты своих исследований только после того, как они получали тщательную и весьма совершенную обработку. Но главную роль, несомненно, играли опасения, что эти странные н своеобразные идеи будут встречены враждебно. В январе 1829 г., т. е. тогда, когда Лобачевский уже публиковал мемуар «О началах геометрии» со своими развернутыми исследованиями, Гаусс писал Бесселю:

«Вероятно, я еще нескоро смогу обработать свои пространные исследования по этому вопросу, чтобы их можно было опубликовать. Возможно даже, что я не решись на это во всю свою жизнь, потому что я боюсь крика беотийцев, который поднимется, когда я выскажу1 свои воззрения целиком».

Крика беотийцев Гаусс действительно избежал, потому что об этих своих воззрениях он ничего при жизни не опубликовал. В его наследии сохранились лишь отдельные фрагменты — наброски начальных предложений неевклидовой геометрии. Эти фрагменты воспроизведены в томе VIII сочинений Гаусса; достаточно их просмотреть, чтобы уяснить себе, как незначительно то, что оставил в этой области Гаусс, по сравнению с творениями Лобачевского.

Эта переписка с Тауринусом имела свою предысторию. С 1812 по 1816 г. в Харькове состоял профессором права Фердинанд Швейкарт (1780—1857). Посвящая свой досуг геометрии, Швейкарт еще раньше заинтересовался теорией параллельных линий и в 1807 г. опубликовал работу, содержавшую доказательство V постулата⁵. Убедившись затем в неправильности этого доказательства, Швейкарт во время своего пребывания в Харькове пришел к воззрениям, которые можно рассматривать как первое предвосхищение идей Лобачевского. В 1817 г. Швейкарт был приглашен в Марбург, где сблизился с профессором Герлингом и через него препроводил Гауссу заметку следующего содержания:

«Существует двоякая геометрия: геометрия в узком смысле слова, евклидова, и звездная (astralische). Треугольники последней геометрии имеют ту особенность, что сумма трех углов не равна двум прямым. Принимая это, можно самым точным образом доказать следующее: а) что сумма трех углов в треугольнике меньше двух прямых; b) что сумма эта тем меньше, чем больше площадь треугольника; с) что высота прямоугольного равнобедренного треугольника, постоянно возрастая с возрастанием сторон, не может превзойти некоторую линию, которую я называю константой. Квадраты имеют поэтому следз'ющий вид (рис. 36).

Если же константа для нас равна радиусу Земли (в каковом случае всякая линия, проведенная в пространстве от одной неподвижной звезды к другой, отстоящей от нее на 90°, была бы касательной к земному шару)⁶, то она бесконечно велика по сравнению с протяжениями, которые мы встречаем в повседневной жизни. Евклидова геометрия имеет место только в том случае, если константа бесконечно велика. Только в этом случае сумма углов каждого треугольника равна двум прямым, и это легко доказать, если принять, что константа бесконечно велика».

Для осведомленного человека совершенно ясно, что в этих словах содержатся первые зачатки геометрии Лобачевского. Прежде всего поясним основное соображение, высказанное Швейкартом. Представим себе равнобедренный треугольник АС В с прямым углом при вершине С (рис. 37). Биссектриса CD служит его высотой. Будем теперь высоту CD увеличивать: будем сначала получать равнобедренные треугольники А'С В', А''СВ'',... с возрастающими боковыми сторонами. Однако в плоскости Лобачевского, когда высота достигнет значения h = CD, для которого П(А) =45°, перпендикуляр к CD уже перестанет пересекать прямые С А и СВ, равнобедренного треугольника уже не получится. Швейкарт это именно и предусматривает в пункте (с) своего сообщения; h — это та постоянная, о которой он говорит, — постоянная, которая в той или иной форме выплывает в неевклидовой геометрии.

Гаусс ответил: «Заметка профессора Швейкарта доставила мне необычайно много удовольствия, и я прошу сказать ему по этому поводу от меня много хорошего. Все это как будто выписано из моей собственной души».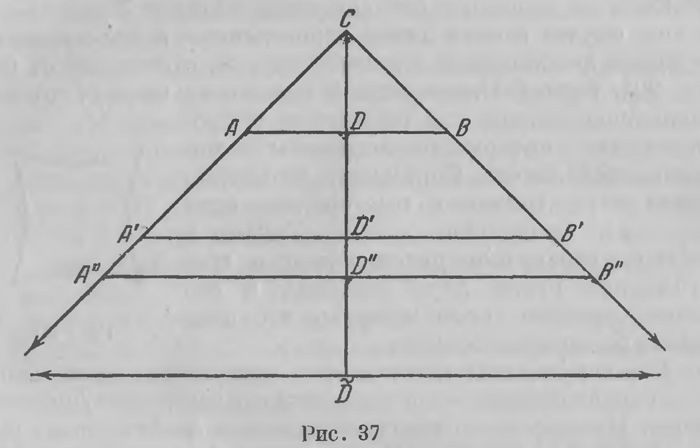

Гаусс тут же приводит даже некоторые начальные предложения неевклидовой геометрии. Это письмо характерно больше для Гаусса, чем для Швейкарта. Из него видно, что в начале 1819 г. Гаусс уже владел первыми основами неевклидовой геометрии. Швейкарт, по-видимому, недостаточно владел математикой, чтобы продвинуться в развитии новой геометрии значительно дальше того, что изложено в его записке к Гауссу.

В переписке со своим племянником Тауринусом, в то время также изучавшим юридические науки, Швейкарт сообщил последнему о своих занятиях теорией параллельных линий и в общих чертах познакомил его с теми результатами, к которым он пришел. Тауринус отнесся к этому сначала безучастно, но через несколько лет, случайно познакомившись с упомянутой выше брошюрой Швейкарта, он с увлечением занялся теорией параллельных линий. Имея в виду доказать постулат от противного, он исходит из допущения, что сумма углов треугольника меньше 2d, и делает отсюда ряд выводов. Зная от Швейкарта, что вопросы этого рода интересуют Гаусса, Тауринус послал ему заметку, содержавшую первые результаты его исследований. В чем собственно его результаты в ту пору заключались, осталось неизвестным, так как письмо его пе сохранилось. Ответное письмо Гаусса помещено выше почти полностью. Как и все письма Гаусса, оно говорит больше о его собственных достижениях, чем о результатах, полученных его корреспондентом. Во всяком случае благожелательный тон Гаусса побудил Тауринуса продолжать свои занятия теорией параллельных линий, в результате чего он в 1825 г. опубликовал брошюру, посвященную этому вопросу⁷.

В следующем, 1826 г. он опубликовал новую брошюру, содержавшую тот же материал в исправленном и дополненном виде⁸. Извлечения из обеих брошюр помещены в «Собрании первоисточников» Штеккеля и Энгеля. Стремясь, как указано выше, доказать постулат о параллельных от противного, Тауринус также пришел к константе Гаусса и Швейкарта и близко подошел к тригонометрии неевклидова пространства; фактически он решает ряд задач, относящихся к неевклидовой геометрии. Методы вычисления тяжеловесны, изложение сжато и мало вразумительно. Это в значительной мере обусловливалось тем, что Тауринус не отдавал себе сам полного отчета в содержании и значении проблем, решением которых он занимался.

В предисловии к своей последней брошюре Тауринус в осторожной форме высказывает пожелание, чтобы Гаусс опубликовал свои взгляды на основы геометрии. Брошюры были, конечно, посланы Гауссу, но последний усмотрел в словах Тауринуса, помещенных в предисловии, нарушение его воли и прекратил о ним какие бы то ни было сношения. Не встретив ни малейшего признания своих идей, Тауринус впал в меланхолию; в припадке болезни он сжег оставшиеся у него экземпляры брошюр. В Европе сохранилось лишь несколько экземпляров этих брошюр. Энгель разыскал их и опубликовал то материалы, которые представляют интерес, в «Собрании первоисточников».

Во время своего учения в Геттингене Гаусс сблизился с прибывшим из Венгрии студентом Вольфгангом (Фаркасом) Больаи (Wolfgang Bolyai, 1775 — 1856)— нам ужо приходилось о нем упоминать. В студенческие годы друзья вели многочисленные беседы по разным вопросам математики, главным образом по ее основаниям. В 1799 г. В. Больаи окончил университет и вернулся на родину. В 1804 г. он был назначен профессором математики в коллегии в г. Марош-Вашаргели и занимал этот пост почти 50 лет. Это был очень живой, несомненно одаренный человек, с весьма разносторонними интересами. Он старался способствовать развитию мадьярского языка, увлекался поэзией, музыкой, сельским хозяйством. Но более всего интересы его принадлежали математике. После возвращения из Германии В. Больаи вел интенсивную переписку с Гауссом, которая, однако, с годами стала замирать; тем не менее время от времени Вольфганг обращался к Гауссу с различными вопросами, относящимися к основаниям математики. Два раза Вольфганг посылал Гауссу доказательства постулата о параллельных, из которых первое относилось еще к 1799 г.; это было, таким образом, очень скоро после того, как они расстались в Геттингене. Ответ Гаусса на это первое обращение мы уже привели выше; он содержал указания на новые воззрения Гаусса относительно евклидовой геометрии.

В 1832—1833 гг. Вольфганг Больаи выпустил в свет учебное руководство по основам математики как элементарной, так и высшей, под названием «Опыт введения учащегося юношества в начала чистой математики»⁹. Первое слово этого заглавия —«Опыт» (по-латыни «Теntamen») служит кратким названием, под которым это сочинение известно в литературе. К первому тому, появившемуся в 1832 г., было присоединено приложение, принадлежащее его сыну Иоанну Больаи.

Иоанн Больаи родился в 1802 г.; детство и юность он провел в доме отца, обучался под его непосредственным руководством в той же коллегии, где отец был профессором. Юноша несомненно обнаруживал большие способности, особенно к математике. Мечтой отца было послать Иоанна для продолжения образования в Геттинген к Гауссу. Однако для осуществления этого намерения необходимы были значительные средства, которыми Больаи не располагал. Он обратился поэтому к Гауссу с письмом, в котором просил его взять Иоанна к себе, с тем что он покроет расходы по его содержанию. На это письмо ответа не последовало; Гаусс не счел даже нужным объяснить, почему он отклоняет просьбу. Отец и сын очень тяжело это пережили; но выхода не было, и отец определил Иоанна в инженерную академию в Вене, где он обучался на казенный счет. Здесь очень скоро обнаружились выдающиеся математические способности Иоанна, но в то же время его задорный и неуживчивый нрав. В 1823 г. он был произведен в офицеры и послан в небольшой венгерский город Темешвар, а позже переводился в другие гарнизоны. Годы своей службы, продолжавшейся до 1833 г., Иоанн прожил в глубоком уединении. Со своими сослуживцами он не ладил; был случай, когда он в один день выдержал двенадцать дуэлей на рапирах.

В отставку он тоже должен был выйти вследствие конфликта с таможенными чиновниками. Во все эти годы его интересы принадлежали математике. Не имея никакого руководства, совершенно не будучи осведомлен о проблемах, которые в то время занимали выдающихся математиков, Иоанн размышлял главным образом над вопросами элементарной математики, которые являлись камнем преткновения того времени — прежде всего над теорией параллельных линий. Стимулом к этому послужили давнишние беседы с отцом.

Весной 1820 г. Иоанн пишет отцу о своей попытке доказать XI аксиому. Это извещение приводит отца в отчаяние. В ответном письме, которое мы выше уже приводили (стр. 168) по другому поводу, он настойчиво убеждает сына оставить безнадежные попытки доказать постулат о параллельных линиях. Увещания отца, однако, не были в состоянии отвлечь Иоанна от занятий теорией параллельных линий. По его собственным словам, он считался больше со словами Сенеки: «suspice viros, etsi deciderint, magna conantes» (почитай мужей, много дерзающих, даже если они терпят крушение). Иоанн дерзал, и в результате к 1825 г. он по существу уже владел началами новой, неевклидовой геометрии. Но для того чтобы довести исследование до конца, оформить, изложить полученные результаты, потребовалось еще около десяти лет. Посвященное этому небольшое сочинение было готово к тому времени, когда отец выпускал в свет свой «Тентамен». Выло решено, что работа Иоанна появится в виде приложения к «Тентамену». Как и «Тентамен», работа была написана на латинском языке. «Приложение»— по-латыни «Appendix»; поэтому сочинение Иоанна Больаи известно в литературе под названием «Аппендикс». Оно содержало весьма сжатое изложение основ неевклидовой геометрии. «Тенгамен» вышел в свет в 1832 г. Отец не был в состоянии овладеть идеями сына, и между ними возник на этой почве очень острый спор. Для разрешения спора Иоанн предложил послать работу Гауссу, суд которого уяснит значение его работы. После пятнадцатилетнего перерыва Вольфганг Больаи написал Гауссу, послал ему работу сына и просил сообщить свое мнение о ней. Получив «Аппендикс», Гаусс на следующий же день написал Герлингу:

«Ha днях я получил из Венгрии небольшое сочинение по неевклидовой геометрии; я нашел в нем все свои собственные идеи и результаты, выведенные о большим изяществом». Этот лейтмотив, что это собственно его идеи, которым он за недостатком времени не успел дать достаточного развития, проходит через все письма Гаусса по вопросам, связанным с открытием неевклидовой геометрии. Особенно четко он звучит в ответе Вольфгангу Больаи, который последовал только через месяц после получения письма и «Аппендикса». После сообщений дружеского и семейного свойства Гаусс переходит к работе Иоанна и пишет»

«Теперь кое-что о работе твоего сына. Если я начну с того, что я эту работу не должен хвалить, то ты, конечно, на минуту поразишься: но иначе не могу; хвалить ее значило бы хвалить самого себя: все содержание сочинения, путь, по которому твой сын пошел, и результаты, которые он получил, почти сплошь совпадают с моими собственными достижениями, которые частично имеют уже давность в 35 лет. Я, действительно, этим в высшей степени поражен. Моим намерением было о моей собственной работе, которая, впрочем, До настоящего времени очень мало нанесена на бумагу, при жизни ничего не публиковать. Большинство людей не имеет правильных воззрений на те вопросы, о которых здесь идет речь; я нашел лишь мало людей, которые с особым интересом отнеслись к тому, что я им сообщал по этому предмету. Чтобы быть в состоянии это усвоить, нужно прежде всего весьма живо прочувствовать то, чего здесь собственно не хватает; а это большинству людей совершенно не ясно. Однако я имел намерение со временем изложить все это на бумаге в такой форме, чтобы эти идеи по крайней мере не погибли со мной. Таким образом, я чрезвычайно поражен тем, что эта работа с меня снимается, и я в высшей степени рад, что именно сын моего старого друга предупредил меня таким замечательным образом».

Это письмо произвело на Иоанна Больаи удручающее впечатление. Сначала он не хотел верить, что Гаусс раньше его пришел к этим идеям; он считал, что Гаусс склонен вырвать у него приоритет этого открытия. «Вырвать»— может быть, сказано слишком сильно. Но в письмах Гаусса всегда звучит мысль, что идеи эти принадлежат собственно ему; что только недостаток времени лишает его возможности этот материал обработать. Вообще в его отношении к корреспондентам нет и следа заботы о молодых авторах, жаждущих его поддержки. Иоанна Больаи особенно волновало то, что Гаусс не нашел нужным обмолвиться в печати об этих замечательных идеях. В заметках, оставшихся после его смерти, находятся следующие строки, полные глубокой горечи и совершенно справедливой обиды:

«По моему мнению и, как я убежден, по мнению всякого непредубежденного человека, все доводы, приводимые Гауссом в объяснение того, почему он при жизни совершенно не желает ничего опубликовать из своих собственных работ, относящихся к этому вопросу, совершенно бессильны и ничтожны. Ведь в науке, как и в повседневной жизни, задача заключается именно в том, чтобы необходимые, общеполезные вещи, в особенности еще не вполне ясные, достаточно осветить и всемерно будить еще недостаточное или даже дремлющее сознание истины и права; это именно нужно крепить и развертывать. Понимание математики, к общему вреду и неблагополучию, присуще, хк сожалению, лишь очень немногим; и ведь по такому основанию и под таким предлогом Гаусс мог бы последовательно сохранить про себя еще значительную часть своих превосходных работ. То обстоятельство, что, к сожалению, среди математиков, и даже среди знаменитых, имеется еще много поверхностных людей, конечно, не может служить основанием для того, чтобы и в дальнейшем давать только поверхностное и посредственное и оставлять науку в летаргии, в унаследованном ее состоянии. Такого рода умонастроение нужно было бы назвать противоестественным и совершенно бессмысленным. Производит крайне неприятное впечатление, что Гаусс, вместо того чтобы высказать относительно «Аппендикса» и всего «Тентамена» от себя прямое, честное признание их высокой ценности, чтобы дать выражение своей радости и своему участию, чтобы подумать о тех средствах, которые проложили бы хорошему делу широкий путь,— что Гаусс вместо всего этого старается избегать прямого пути и спешит излиться в благочестивых пожеланиях, в выражениях сожаления по поводу недостаточного образования людей. Не в этом, конечно, заключается жизнь и действенная заслуга».

Очень характерно, что эти полупритязания Гаусса на приоритет проявились не только в вопросе об открытии неевклидовой геометрии. Они сказались и в вопросе о создании теории эллиптических функция, которое относится почти к тому же времени, когда впервые строилась неевклидова геометрия. Творцами этой теории, как известно, были Абель и Якоби. В 1827—1828 гг. Абель прислал Креллю свою работу, содержавшую учение о приведении эллиптических интегралов к каноническому виду, об обращении интегралов 1-го рода и о двойной периодичности эллиптических функций. Крелль препроводил эту работу Гауссу. В ответном письме Гаусс сообщал, что он уже около 30 лет владеет этими идеями.

«Другие занятия,— писал он,— помешали мне обработать эти исследования. Абель предвосхитил почти треть моих результатов. Он пошел по пути, которому я следовал уже с 1798 г.¹⁰ Я не удивляюсь поэтому, что он достиг большей части тех же результатов. Так как, однако, в своей дедукции он проявил столько таланта и изящества, то я освобожден от необходимости обрабатывать собственные результаты».

Тот же лейтмотив, в котором автор до некоторой степени отходит на задний план. А вот отзыв о той же работе Якоби, который в то время также с успехом занимался теорией эллиптических функций: «Работа Абеля выше моих похвал, как она выше моих работ». Отзыв Гаусса вызвал во Франции большое раздражение.

Поскольку речь зашла об отношениях между Гауссом и Абелем, здесь будет уместно сказать несколько слов и о другом инциденте, осложнившем эти отношения и характерном для поведения Гаусса в делах, которые очень волновали молодых ученых; это будет тем более уместно, что проливает некоторый свет и на те переживания, которые выпали на долю Лобачевского.

Приблизительно в то же время, когда размышления о теории параллельных линий привели Лобачевского к открытию неевклидовой геометрии, Абель был поглощен другой проблемой, которая также в течение столетий служила камнем преткновения для математической мысли: это был вопрос о решении в радикалах общего уравнения пятой степени. В 1824 г. Абель пришел к заключению, что такое решение для уравнений, степень которых выше четырех, невозможно. Он изложил это в мемуаре, озаглавленном «Memoire sur les equations algebriques ou on demontre l'impossibilite de la resolution de 1’equation generale du cinquieme degre». Этот замечательный мемуар также содержал совершенно неоншданный результат, который составил эпоху не только в истории алгебры, но даже за пределами этой дисциплины. Мемуар был через Шумахера послан Гауссу, после смерти которого был обнаружен в его литературном наследии. Однако Гаусс не одобрил этой работы, во всяком случае ни в какой форме не дал этому выражения. Напротив, есть указание (Hansteen), что Гаусс, не будучи убежден в правильности рассуждений Абеля, был склонен сам заняться этим вопросом.

«Так или иначе,— замечает биограф Абеля Биеркнесс¹¹, — молодой студент, который в наивном напряжении надеялся услышать поддержку со стороны великого человека, в лучшем случав не услышал ничего. Это послужило для Абеля основанием для раздражения против Гаусса». Крелль, которому также был послан мемуар, в нем тоже не разобрался, и мемуар был опубликован только значительно позднее. В 1826 г,, находясь в Берлине в научной командировке, Абель писал своему учителю и ДРУГУ Гольмбоэ (Holmboe): «До конца февраля или марта я, повидимому, останусь в Берлине, а затем через Лейпциг и Галле поеду в Геттинген,— не ради Гаусса, который, говорят, невыносимо горд, а ради библиотеки». Тот же мотив повторяется и в других письмах Абеля. Суров был Гаусс по отношению к молодым ученым.

Возвратимся, однако, к Больаи. Исследованию жизни, работ и литературного наследия обоих Больаи посвятил много лет своей жизни германский математик П. Штеккель, выпустивший большое сочинение, посвященное отцу и сыру Больаи. Оно включено в «Собрание первоисточников», которое мы уже не раз цитировали, и состоит из двух частей: первая часть посвящена жизнеописанию и обзору сочинений обоих Больаи, второе содержит извлечения из их работ¹², в том числе «Аппендикс» в переводе на немецкий язык. Это издание содержит весьма обильный математический и литературный материал и представляет очень ценный вклад в историю неевклидовой геометрии. Отсылая к этому сочинению читателей, желающих ближе познакомиться с материалом, мы вкратце остановимся на тех моментах последующей жизни Иоанна Больаи, которые связаны с творчеством Лобачевского.

Главный труд его жизни —«Аппендикс»— оставался совершенно не известным. Отчасти это обусловливалось тем, что его работа была помещена в качестве приложения к большому, дорого стоившему «Тентамену», который не получил значительного распространения. Но главная причина этого заключалась в том, что «Аппендикс» был написан на латинском языке и изложен чрезвычайно сжато и схематично,— он не был доступен.

Как мы знаем, Лобачевский после опубликования первых своих работ составил большое сочинение «Новые начала геометрии», в которых старался перестроить всю геометрию сначала до конца на новых основаниях. Больаи также предпринял совершенно аналогичную работу. Оп решил составить обстоятельное сочинение —«Учение о пространстве» («Raumlehre»), имевшее ту же задачу — построить всю геометрию на новых основаниях. Выдержки из сохранившихся рукописей этого сочинения помещены в книге Штеккеля. Эта работа была прервана тем, что Иоанн Больаи принял участие в соискании премии Лейпцигского ученого общества имени Яблоновского. Тема, предложенная Обществом, требовала улучшения в геометрическом построении теории мнимых чисел. Больаи представил Обществу краткую работу, несомненно очень интересную по своему содержанию. Быть может, именно геометрическая сторона была недостаточно выдержана, но по существу она представляла собой предвосхищение идей Грасмана и Гамильтона. Однако своеобразная манера Иоанна — крайняя сжатость изложения и схематическое построение — привели к тому, что работа не была понята. В премии ему было отказано, как и отцу, который также участвовал в конкурсе. Новое разочарование осложнилось еще тем, что на этой почве у него возникли распри с отцом, продолжавшиеся до самой смерти Вольфганга Больаи.

Но к концу жизни Иоанна Больаи постиг новый удар, который он очень тяжело пережил: 17 октября 1841 г. Иоанн получил от отца небольшую брошюру на немецком языке, принадлежавшую Лобачевскому и носившую название: «Geometrische Untersuchungen zur Theorie der Parallellinien».

Это сочинение, как мы знаем, вышло в свет в 1840 г. Но во вступлении Лобачевский указывал, что содержавшиеся в этом сочинении идеи были уже изложены ранее в ряде работ на русском языке, первая из которых появилась в свет в «Казанском вестнике» в 1829 г., следовательно, за три года до опубликования «Аппендикса». Сочинение содержало своеобразное изложение той самой геометрической системы, которую Иоанн разработал в лучшие годы своей жизни. Приоритет опубликования неевклидовой геометрии явно принадлежал Лобачевскому.

Мысли и соображения, которые это сочинение вызвало у Иоанна, сохранились в его обстоятельных примечаниях к «Геометрическим исследованиям». Эти замечания опубликованы Штеккелем, который расшифровал рукописи Больаи в сотрудничестве с его соотечественником профессором Кюршаком¹³. Иоанн тщательно изучил сочинение Лобачевского и проанализировал каждую его строчку, даже каждое его слово с той же тщательностью, с какой он обрабатывал своп «Аппендикс». Сочинение Лобачевского вызвало целую бурю в его душе. В своих подробных замечаниях он дает этим переживаниям свободное выражение. В отличие от всех остальных работ Иоанна, эти заметки были составлены на венгерском языке, вероятно потому, что Иоанн, как он сам об этом упоминает, не предназначал их для печати. Мало того, они написаны особым латинизированным алфавитом, который составили отец и сын с широким замыслом создать интернациональный язык.

Замечания к «Геометрическим исследованиям», как уже сказано, представляют собой не только критический анализ этого сочинения. Это — изложение мыслей и переживаний Иоанна Больаи, вызванных изучением этого сочинения. Они содержат сетования его на то, что он обойден, его подозрения, что никакого Лобачевского в действительности не существует и что все это злобные козни Гаусса; это — трагический вопль души геометра, сознававшего величие своего творения и не получившего поддержки того единственного человека, который был в состоянии его заслуги оценить. Заметки содержат попутные соображения о том, как было бы лучше всего излагать те или иные части неевклидовой геометрии. Но основное их содержание все же составляют обширные критические замечания, написанные в чрезвычайно придирчивом тоне. Однако при всем душевном возбуждении, в котором Больаи писал свои замечания, он сохраняет достаточно объективности, чтобы очень высоко оценить творение своего соперника. В примечаниях к приложению 35 он говорит, что вывод сферической тригонометрии, принадлежащий Лобачевскому, несет на себе печать гения, что его работу нужно признать мастерским произведением. Каких-либо действительно слабых мест в работе Лобачевского Больаи не обнаружил. Наиболее серьезны его замечания к предложению 36. Нужно сказать, что здесь, действительно, имеется существенная недоговоренность, о которой мы уже упоминали (гл. XV). Она заключается в том, что Лобачевский, дважды употребляя букву е для обозначения оснований показательных функций, к которым его приводят исследования, не доказывает, что эти основания в обоих случаях имеют одно и то же значение (см. стр. 202). Если оставаться только при тексте «Геометрических исследований», то это несомненный пробел. Однако этот пробел (см. стр.359) совершенно восполнен в других сочинениях Лобачевского, и в сущности даже до появления «Геометрических исследований», что Штеккель и обнаруживает надлежащими сопоставлениями.

Большой интерес представляют принципиальные соображения Больаи по вопросу о том, насколько можно считать установленным, что неевклидова геометрия не содержит в себе внутренних противоречий. Этот чрезвычайно трудный вопрос занимал Лобачевского в течение всей его жизни. Его обширные интегральные вычисления, как мы видели, имеют главной своей целью обнаружить постоянное совпадение результатов и тем подтвердить незыблемость новой геометрии. Относящиеся сюда краткие соображения, которые мы находим в «Геометрических исследованиях», Больаи не удовлетворяют, и, конечно, не без оснований. Больаи утверждает при этом, что им найдено безукоризненное доказательство, как теперь говорят, непротиворечивости неевклидовой геометрии. Однако никаких следов такого доказательства он не оставил; совершенно не видно, как он к этой задаче подходил. Вряд ли можно сомневаться в том, что это была иллюзия.

Решение вопроса о логической правильности геометрической системы требовало глубоких новых идей, которыми творцы неевклидовой геометрии еще не владели. Они создали для этого главные математические средства, но довести задачу до конца было уже уделом их последователей.

Сведения, принесенные перепиской Гаусса с друзьями, послужили для некоторых германских математиков основанием утверждать, что открытие неевклидовой геометрии по существу принадлежит Гауссу, что другие авторы, которым приписывается открытие неевклидовой геометрии, фактически заимствовали свои идеи у Гаусса. Эту точку зрения отстаивал покойный Ф. Клейн. В первом литографированном изДании своей «Неевклидовой геометрии» он говорил.

«Не подлежит никакому сомнению, что именно он (Гаусс) своим влиянием вызвал исследования Лобачевского и Больаи, ибо новые идеи возникли в умах этих людей не самостоятельно (sua sponte), а вследствие личных, хотя и частично косвенных связей с Гауссом». Это утверждение мотивировалось обыкновенно следующими соображениями. Гаусс пришел к своим взглядам на теорию параллельных линий и возможность новой геометрии еще до поступления в Геттингенский университет. В Геттингене он, вероятно, имел об этом беседы с Вольфгангом Больаи и сообщил ему свои идеи. От Вольфганга они перешли к Иоанну Больаи, который дал этим идеям развитие.

Что касается Лобачевского, то здесь, по мнению тех, кто поддерживал эту версию, посредствующую роль мог играть Бартельс. Предполагается, следовательно, что Бартельс был осведомлен относительно взглядов Гаусса на основания геометрии, и от него Лобачевский мог получить толчок в направлении этих идей. Однако тщательный анализ обнаруживает полную несостоятельность всей этой версии.

Прежде всего, Вольфганг Больаи, как мы уже знаем, получив от сына «Аппендикс», не только не усвоил его идей, но категорически их оспаривал; между тем, при том благоговении, с каким он относился к Гауссу, он ни в каком случае не мог бы занять такой позиции, если бы в его памяти сохранилось какое-нибудь воспоминание о взглядах Гаусса. Эти общие соображения безусловно подтвердились при тщательном анализе эволюции взглядов Иоанна Больаи, произведенном Штеккелем.

По отношению к Лобачевскому такой же анализ проведен Ф. Энгелем в его сочинении, посвященном Лобачевскому (см. стр. 7). Тщательно сопоставляя даты, Энгель приходит к твердому убеждению, что ни малейшего влияния на развитие идей Лобачевского Бартельс не имел. Бартельс уехал из Германии в 1807 г., т. е. в то время, когда взгляды Гаусса на основы геометрии, в частности, на учение о параллельных линиях, еще далеко не установились. Мы видели выше, что это было время, когда Гауссом владели еще колебания и сомнения, и он не исключал возможности доказать постулат о параллельных линиях. Единственно, что он мог бы в это время сообщить Бартельсу, это давно зародившееся у него сомнение относительно безусловной истинности евклидовой геометрии. Бартельс находился в переписке с Гауссом, переписка эта носила спорадический характер, обмен письмами происходил через большие промежутки. Письма Гаусса у Бартельса не сохранились, но аккуратный Гаусс сохранил все письма Бартельса. Это все сообщения личного характера, никакие математические вопросы в них не затрагиваются; совершенно ясно, что математического общения между Гауссом и Бартельсом в ту пору не было. Оно и естественно: Бартельс, как мы уже не раз указывали, был человек, владевший углубленным математическим образованием, выдающийся преподаватель швейцарской школы, чрезвычайно добросовестный и полезный преподаватель Казанского университета; но к математическому творчеству он не приобщился. Между тем Гаусс вел математическую переписку, вообще находился в математическом общении только с людьми творческого типа. В 1803 г. Бартельс и Гаусс обменялись письмами, судя по письму. Бартельса, несомненно тоже бытового содержания. После этого переписка между ними прерывается до 1821 г.; из письма Бартельса видно, что никаких писем он в течение этого времени от Гаусса не получал. Между тем Лобачевский обращается к вопросу о параллельных линиях в 1817 г. и сообщает своим студентам доказательство постулата о параллельных линиях. Он идет, таким образом, обычным путем, и никаких следов тех сомнений, которые владели Гауссом, не обнаруживает. Только из его «Геометрии» можно заключить, что ни одно из предложенных доказательств постулата о параллельных линиях его уже (в 1823 г.) не удовлетворяло.

Таким образом, в годы своего общения с Лобачевским Бартельс не мог располагать сколько-нибудь отчетливыми сведениями о сложившихся воззрениях Гаусса на учение о параллельных линиях. С другой стороны, в распадениях Лобачевского до 1823 г. нельзя еще усмотреть никакого следа сомнений в безусловной и непоколебимой истинности евклидовой геометрии.

Если на протяжении всего этого времени нельзя проследить ни одного момента, который дал бы основание считать, что Бартельс получил какие-либо сведения от Гаусса о его взглядах на вопрос о параллельных линиях и сообщил о них Лобачевскому, то последующие данные совершенно исключают эту возможность. Опубликовав свои работы, Лобачевский, естественно, послал их своему учителю. В 1835 г. Бартельс уже располагал первыми сочинениями Лобачевского. Но, по сообщению известного астронома О. В. Струве (в письме к Энгелю), Бартельс отнесся «к остроумным спекуляциям» Лобачевского отрицательно и не признавал за ним никакого научного значения. Это было бы невозможно, если бы Бартельсу были известны взгляды Гаусса на этот предмет, и, в особенности, если бы Бартельс сам сообщил о них Лобачевскому. Вся совокупность этих соображений не оставляет сомнений в том, что Лобачевский пришел к своим замечательным идеям совершенно самостоятельно.

По-видимому, эти соображения нашел убедительными и Клейн; в печатном издании «Неевклидовой геометрии» он уже прежних соображений не повторяет.

Переписка Гаусса вскрыла ряд работ, совокупность которых можно рассматривать как предысторию неевклидовой геометрии. К этой предистории следует отнести и рассуждения Лежандра, его «Размышления», которым Лобачевский уделяет много внимания. Рассуждения Лежандра, как мы видели, установили связь между теоремой о сумме углов треугольника и теорией параллельных линий. В дополнение к тому, что было сделано уже Наеир-Эддином, Лежандр доказал, что сумма углов треугольника не может быть больше двух прямых и что она либо во всех треугольниках равна двум прямым, либо во всех треугольниках меньше двух прямых. Эта дилемма считалась существенным достижением Лежандра и в течение Долгого времени неизменно связывалась с его именем. Но в 1889 г. известный итальянский геометр Е. Бельтрами, которому, как увидим, вопросы неевклидовой геометрии в то время были очень близки, обратил внимание на замечательное, но мало известное сочинение итальянского иезуита Иеронима Саккери, в котором все результаты Лежандра пе только уже были опубликованы, но даже получили значительно большее развитие. Это сочинение есть издание «Начал» Евклида с широковещательным заглавием: «Евклид, освобожденный от всех пятен, или опыт, устанавливающий самые первые принципы универсальной геометрии»¹⁴. Оно было опубликовано в 1733 г., уже после смерти автора, умершего в том же году. Тонко анализируя Евклида, Саккери очень подробно останавливается на постулате о параллельных линиях и действительно дает этому вопросу существенно новое освещение.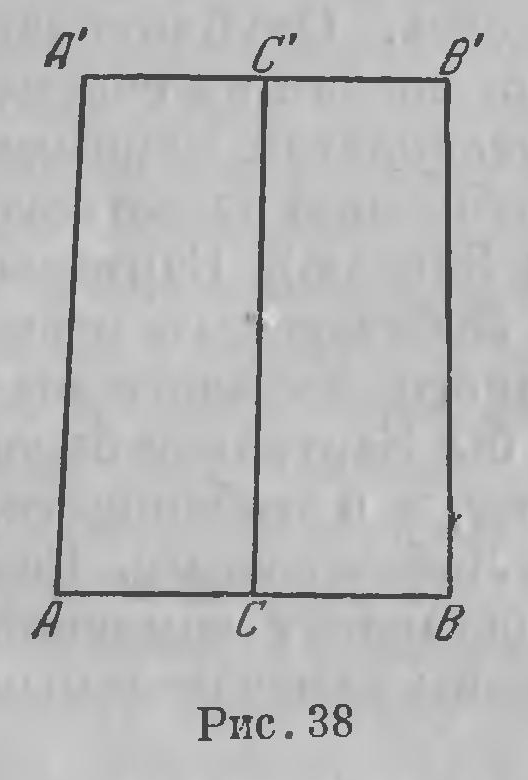

Точкой отправления для Саккери служит четырехугольник, который фактически встречается уже у Насир-Эддина. Из крайних точек А и В отрезка АВ восставим к нему перпендикуляры АА' и ВВ', расположенные в одной плоскости по одну сторону прямой АВ. На этих перпендикулярах отложим равные отрезки АА' и ВВ' (рис. 38). Таким образом составится четырехугольник АА'В'В с двумя прямыми углами при нижнем основании АВ. С четырехугольником этого типа нам уже приходилось встречаться (гл. XVII, стр. 231). Соединим середины С и С' оснований АВ и А'В'; налагая четырехугольник АА'В'В на себя другой стороной (ВВ'А'А), докажем, что прямая СС' перпендикулярна к обоим основаниям, а углы А' и В' равны между собой. Относительно этих углов может быть сделано три предположения: либо эти углы тупые, либо они прямые, либо острые. Саккери показывает прежде всего, что, принимая то или другое предложение относительно одного четырехугольника этого типа, мы тем самым должны принять его также относительно всех четырехугольников того же типа. Иными словами, если какой-либо один из этих четырехугольников имеет при верхнем основании, скажем, острые углы, то и все четырехугольники этого типа имеют острые же углы. Саккери называет три различных допущения которые здесь могут быть сделаны, «гипотезой острого угла», «гипотезой прямого угла» и «гипотезой тупого угла». Саккери доказывает далее, что при гипотезе тупого угла сумма углов всякого треугольника больше двух прямых, при гипотезе прямого угла она равна двум прямым, при гипотезе острого угла она меньше двух прямых. Далее доказывается, что гипотеза прямого угла эквивалентна постулату Евклида; чтобы доказать постулат, нужно, следовательно, опровергнуть две другие гипотезы. Но если принять гипотезу тупого угла, то прямые А'В' и АВ сближаются по обе стороны прямой СС и сближаются настолько быстро, что по обе стороны должно произойти пересечение (Саккери это доказывает вполне строго); а так как две прямые не могут пересекаться в двух точках, то гипотеза тупого угла отпадает. Остается опровергнуть гипотезу острого угла. Этой гипотезе Саккери посвящает обширное исследование, занимающее около 80 страниц. Саккери показывает, что при гипотезе острого угла две непересекающиеся прямые, расположенные в одной плоскости, либо имеют общий перпендикуляр, от которого они расходятся, бесконечно удаляясь друг от друга в обе стороны, либо бесконечно удаляются друг от друга в одну сторону и неограниченно сближаются в другую. Чтобы это обнаружить, строится ряд подготовительных рассуждений, часто для дела вовсе ненужных, которые, однако, Саккери проводит с безупречной строгостью. Он показывает при этом, что перпендикуляр к стороне острого угла (при гипотезе острого угла) начала пересекает вторую сторону, а потом, по мере удаления от вершины, перестает ее пересекать; что при этом существует предельный — первый не пересекающий — перпендикз^ляр и т. п. Словом, это целая геометрическая система, соответствующая гипотезе острого угла. Но эта тонкая нить безупречных рассуждений внезапно прерывается теоремой XXXIII, в которой Саккери заявляет: «Гипотеза острого угла совершенно ложна, ибо противоречит природе прямой линии». В чем же сказывается это противоречие? Рассматривая неограниченно сближающиеся прямые как пересекающиеся в бесконечно удаленной точке, Саккери приходит к заключению, что из этой бесконечно удаленной точки к обеим прямым можно было бы провести общий перпендикуляр, что «противно природе прямой линии». Человек, чрезвычайно тонко разбирающий доказательства Прокла, Насир-Эддина и Клавия, искусно вылавливающий глубоко сокрытую логическую ошибку, запутывается сам в элементарных рассуждениях, потому что он не имеет твердых оснований для суждения о том, в какой мере можно пользоваться бесконечно удаленными точками При всей категоричности, с которой формулирована XXXIII теорема, Саккери, очевидно, чувствует слабость этих рассуждений, ибо он заканчивает следующим примечанием:

«На этом я мог бы спокойно остановиться; но я не хочу отказаться от попытки доказать, что эта упорная гипотеза острого угла, которую я вырвал уже с корнем, противоречит самой себе. Этому посвящены следующие теоремы настоящей книги».

Возвращаясь, таким образом, вновь к гипотезе острого угла, Саккери показывает, что геометрическое место точек в плоскости, удаленных на данное расстояние от данной прямой, представляет собой кривую линию («кривая равных расстояний, «эквидистанта», как ее теперь называют). За этим следует подробный анализ этой кривой, совершенно правильный до тех пор, пока он не приступает к определению ее длины при помощи метода бесконечно малых. Здесь он вновь впадает в ошибку, которая заставляет его отвергнуть гипотезу острого угла. Но и здесь он кончает примечанием, указывающим, что и эти рассуждения его, в сущности, не удовлетворяли.

«Не могу не указать здесь,— говорит он,— разницы между приведенными опровержениями обеих гипотез, при гипотезе тупого угла дело ясно, как свет божий... Между тем опровергнуть гипотезу острого угла мне не лается иначе, как доказав, что эта длина равна длине ее прямолинейного базиса».

Аналогичную постановку вопроса мы находим в сочинении математика и философа Генриха Ламберта «Теория параллельных линий», относящемся к 1766 г.¹⁵

Ламберт рассматривает четырехугольник, имеющий три прямых угла (рис. 39) А, С, D; относительно четвертого угла В могут быть опять-таки сделаны три гипотезы: либо это угол тупой, либо прямой, либо острый. Ламберт рассматривает каждую гипотезу в отдельности и в некоторых отношениях уходит значительно дальше Саккери.

Во-первых, Ламберт указывает, С что гипотеза тупого угла оправдывается на сфере, если присвоить окружностям большого круга роль прямых линий: так как окружности эти имеют по две общие точки, то предложение, при помощи которого эта гипотеза отвергается на плоскости, здесь не находит применения.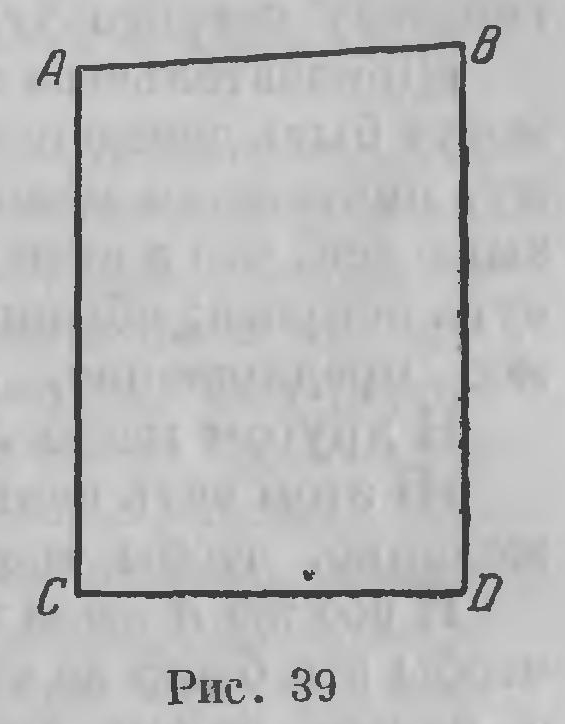

Во-вторых, он ведет гипотезу острого угла еще дальше, нежели Саккери: он знает, например, что при этой гипотезе площадь треугольника должна быть пропорциональна разности между 2d и суммой его углов. Стройность умозаключений, к которым ведет гипотеза острого угла, и в особенности последний упомянутый факт, наводит его на следующее размышление: «Я склонен даже думать, что третья гипотеза справедлива на какой-нибудь мнимой сфере. Должна же быть причина, вследствие которой она на плоскости далеко не поддается опровержению, как это легко может быть сделано со второй гипотезой».

Высокоодаренные люди часто предвосхищают открытия. Слова Ламберта оправдались ровно через сто лет.

В-третьих, наиболее важная заслуга Ламберта заключается в том, что он не впал в заблуждение и не признал достаточным ни одного доказательства, опровергающего гипотезу острого угла.

«Доказательства евклидова постулата,— говорит он,— могут быть доведены столь далеко, что остается, по-видимому, ничтожная мелочь. Но при тщательном анализе оказывается, что в этой кажущейся мелочи и заключается вся суть вопроса; обыкновенно она содержит либо доказываемое предложение, либо равносильный ему постулат».

В другом месте Ламберт восклицает:

«В этом есть нечто восхитительное, что вызывает даже желание, чтобы третья гипотеза была справедлива!

И все же я желал бы, несмотря на это преимущество¹⁶, чтобы это было не так, потому что это было бы сопряжено с целым рядом других неудобств. Тригонометрические таблицы стали бы бесконечно пространными; подобие и пропорциональность фигур не существовали бы вовсе; ни одна фигура не могла бы быть представлена иначе, как в абсолютной своей величине, и астрономии пришлось бы плохо».

Указывая ряд абсурдов с точки зрения наших представлений, к которым приводит гипотеза острого угла, Ламберт замечает, что все это не дает логического доказательства, что все это, как он выражается, argumenta ab amore ас invidia ducta,¹⁷— аргументы, которым не может быть места в геометрии. Как и профессор Кестнер, много занимавшийся теорией параллельных линий, быть может, лучший знаток этого вопроса в XVIII в., как и ученик последнего Клюгель, Ламберт приходит к твердому выводу, что все попытки доказать постулат Евклида ни к чему не привели.

Мы изложили предысторию неевклидовой геометрии в той последовательности, в которой развертывались отдельные ее моменты. Обращаясь теперь к хронологической последовательности их, мы видим, что развитие идей, на базе которых развернулась неевклидова геометрия, происходило в следующем порядке.

Точкой отправления все время служат доказательства постулата о параллельных линиях. Сначала эти доказательства носят наивный характер; потом они становятся все серьезнее в том смысле, что содержащаяся в них погрешность все глубже скрывается. По методу они распадаются, главным образом, на две категории: одни явно предпосылают допущение, эквивалентное постулату Евклида, другие ведут доказательство от противного; иными словами, делается допущение, противоположное постулату, и из него выводят следствия с целью придти к противоречию с установленными уже предложениями. Одни авторы приходят к кажущемуся противоречию очень скоро, усматривая его в том, что выводы резко расходятся с интуицией, с указаниями глаза; но в этом нет логического противоречия с установленными уже предложениями. Другие тонко ведут свою дедукцию, приходят к выводам, которые можно рассматривать как начальные предложения неевклидовой геометрии. Далеко в этом направлении прошли Саккери и Ламберт; последний уже не впал в заблуждение и высказывает даже суждение, которое можно рассматривать как первое предвосхищение неевклидовой геометрии, как признание возможности, что «Начала» Евклида не должны считаться необходимой и единственной системой геометрии. Тверже на эту точку зрения становится Гаусс. Концепция неевклидовой геометрии ему уже ясна. Однако в процессе действительного создания неевклидовой геометрии он делает только первые элементарные Шаги> а главное, эти свои взгляды и результаты он тщательно скрывает, сознательно не делает их достоянием гласности. Его корреспонденты — люди, которые находятся с ним по этим вопросам в научном общении, останавливаются на первых шагах. Отчасти это происходит потому, что они не в состоянии преодолеть те трудности, с которыми связано продвижение в этом направлении, отчасти потому, что они не получают со стороны Гаусса той поддержки, на которую они вправе были рассчитывать, которая была им морально необходима.

Действительными творцами неевклидовой геометрии являются Лобачевский и после него Больаи. Лобачевский первый опубликовал систему неевклидовой геометрии, и притом не только ее основы, но и далеко идущее развитие, указал ее применение к анализу, предусмотрел то значение, которое она может иметь в механике, в естествознании. По сравнению с его работами достижения Больаи представляют только первые элементарные шаги.

Оставляя научную сторону дела и переходя к моральной, нельзя не поставить Лобачевскому в особую заслугу, что он не убоялся «крика беотийцев», не устрашился, как Гаусс, «ос, которые поднимутся над его головой». Не встретив сочувствия, он не сжег своих работ, как Тауринус, не впал в меланхолию, как Больаи. Напротив, он вел огромную административную работу; он жил с людьми и для людей. И в то же время он мужественно боролся за свои идеи всю жизнь, проходя через тяжкие переживания, грубые обиды. Не встретив на своем жизненном пути у себя на родине, можно сказать, ни одного человека, который понял бы и оценил его идеи, он на краю могилы еще раз продиктовал для потомства свое великое научное завещание.

¹P. Stаckel und F. Еngе1. Die Theorie der Parallellinlen von Euklid bis Gauss. Eine Urkundensammlung zur Vorgeschichte der niclit euklidischen Geometrie. Leipzig, 1895.
²P. Stackel. Gauss als Geometer. Nachrichtcn der Gesellschaft der Wissenschaften zu Gottingen. Mat. Phys. Klasse. 1917 (и отдельное издание).
³С. F. Gauрs. Werke, VIII, стр. 157—268.
⁴Так называемая Плэйферова формулировка постулата.
⁵К. Schweikart. Die Theorie der Parallellinien, nebst dem Vorschlageihrer Verbannungaus der Geometric. Leipzig und Jona, 1807,
⁶Если S₁ и S₂ суть две звезды, отстоящие одна от другой на 90°, О — центр Земли, то S₁OS₂ есть треугольник Щвейкарта.
Если высота этого треугольника (константа) равна радиусу Земли, то прямая S₁, S₂ касается поверхности Земли в средней точке А.
⁷F. A. Taurinus. Theorie der Parallellinien. Koln, 1825.
⁸F. A. Tanrinus. Geometriae prima elementa. Koln, 1826.
⁹Tentamen imentutem studiosam in elementa matheseos purae elementaris...introducendi cum oppendice tripliei. Alaros-Vasarhelyini, I—II, 1832—1833.
¹⁰Oeuvres compiles de N. II. Abel. Kristiania, 1839. Вступительная глава Гольмбоэ (В. Нolmboe).
¹¹С. А. Вjеrknеss. N. Н. Abel. Berlin, 1030.
¹²P. Stасkеl. Wolfgang und Johann Bolyai. Geometrische bntersuchungen. Leipzig und Berlin, 1913.
¹³P. Stackel und J. Kurschak. Johann Bolyais Bemerkungen fiber Nicolaus Lobatscliewskijs Geomctrisohe Untersuchungen zur Theorie der Parallellinien. Mathematische und naturwissenschaft-liche Berichte aus Ungarn, 18. Budapest, 1902.
¹⁴G. Sассеri. Euclides ah omni naevo vindicatus sive co-natus geometricus quo sfcabiliuutur prima ipsa unhersae geometriae principia. Mediolani, 1733.
¹⁵И. Г. Ламберт (Johann Heinrich Lambert, 1728—1777) написал ряд выдающихся сочинений по физике, логиье и теории познания. Сочинение «Theorie der Parallellinien» было опубликовано в 1786 г., послe смерти автора, в журнале «Magazin fur die reine und angewandte Mathematik», Leipzig, 1786; помещено также в «Собрании первоисточников» Энгеля и Штеккеля, стр. 152—207.
¹⁶Существование абсолютной меры длины.
¹⁷«Аргументы, вызываемые любовью и недоброжелательством».

<<Назад Вперёд>>

Просмотров: 4761

загрузка...

Другие книги по данной тематике