XXX. Интерпретации неевклидовой геометрии
|
Примерно к тому времени, когда со дня рождения Лобачевского исполнилось 75 лет, его работы сделались известными, его замечательные идеи получили первое признание. Однако все еще оставался неразрешенным вопрос, на котором было сосредоточено внимание Лобачевского в течение всей его жизни. Задача, которую он себе ставил, заключалась в установлении, как теперь говорят, «непротиворечивости» созданной им геометрической системы Это требовало точного доказательства того, что никакое дальнейшее развитие этой системы не может привести к противоречию. Как мы уже видели, такое доказательство Лобачевский усматривал в том, что выводы и заключения, к которым различными путями приводили многообразные геометрические рассуждения, всегда были согласны между собой,— что выводы эти аналитически проистекают из уравнений, несомненно совместных, что значения определенных интегралов, получаемые при помощи неевклидовой геометрии, при чисто аналитической их проверке всегда оказываются правильными. И субъективную уверенность в правильности новой геометрии эти доводы действительно давали. Теперь, когда идеи Лобачевского стали достоянием значительного числа геометров, этой уверенностью проникались все усваивавшие новую геометрию. Но она все еще оставалась в строгом смысле слова логически неоправданной; это была еще вера, а не безупречно установленный научный факт. Между тем противники все еще стояли на том, что вся геометрия Лобачевского—сплошная фантазия, не заслуживающая внимания.
Эта фантазия была в следующую четверть века претворена в реальную действительность. Первым осуществил это итальянский геометр Евгений Бельтрами (1835— 1900). Мы уже говорили выше (стр. 196 — 198) о поверхностях, на которых может быть построена геометрия в том же порядке идей, теми же общими методами, при помощи которых развертывается геометрия на плоскости. Мы видели, что в пространстве Лобачевского (в пространстве, в котором осуществляется его геометрия) существуют три типа такого рода поверхностей: на поверхности шара действует сферическая геометрия; на плоскости имеет место геометрия Лобачевского, а на своеобразных предельных поверхностях — геометрия Евклида. Между тем в нашем обычном евклидовом пространстве существуют только два типа поверхностей, на которых теми же средствами может быть построена внутренняя геометрия: на поверхности шара имеет место та же сферическая геометрия, на плоскости — евклидова геометрия. Не естественно ли предположить, что в евклидовом пространстве должны также существовать поверхности, несущие на себе геометрию Лобачевского? К ответу на этот вопрос привели концепции иного рода, но результат оказался положительным. Оказалось, что в обычном евклидовом пространстве существуют поверхности, которые несут на себе геометрию,— вернее, планиметрию — Лобачевского. Однако это имеет место только при некоторой модификации самой постановки вопроса. Это требует выяснения. К выделению поверхностей, несущих на себе ту или иную геометрию в том смысле, как об этом шла речь выше (гл. XV), привело требование, чтобы на них было возможно свободное передвижение фигур без деформации, чтобы на них было возможно, оставаясь на поверхности, производить наложение одной фигуры на другую. В евклидовом пространстве, как уже сказано, существуют только две поверхности, на которых возможно такое передвижение фигур,— это плоскость и сфера. Но можно это требование несколько ослабить, не изменяя его по существу, и тогда количество поверхностей, ему удовлетворяющих, значительно возрастает. Можно, например, говорить о наложении фигур на поверхности цилиндра: движение фигуры на цилиндрической поверхности будет при этом сопровождаться некоторой деформацией — изгибанием, но никакие размеры ее не будут при этом изменяться. Это становится ясным, если вообразим себе навернутый на цилиндр кусок бумаги, который мы можем передвигать по поверхности этого цилиндра, не подвергая его никаким растяжениям, не образуя на нем никаких складок, подвергая его только изгибанию. Будем теперь на поверхности цилиндра считать равными две фигуры, которые могут быть приведены в совмещение именно таким передвижением, хотя бы сопровождаемым изгибанием. Это вполне естественно, потому что такие две фигуры окажутся также равными (конгруэнтными в обычном смысле этого слова), если обеих развернуть на плоскость. На рис. 40 изображены два треугольника, которые могут быть таким образом приведены в совмещение. При таком условии окажется, что и поверхность цилиндра несет на себе обыкновенную евклидову геометрию. 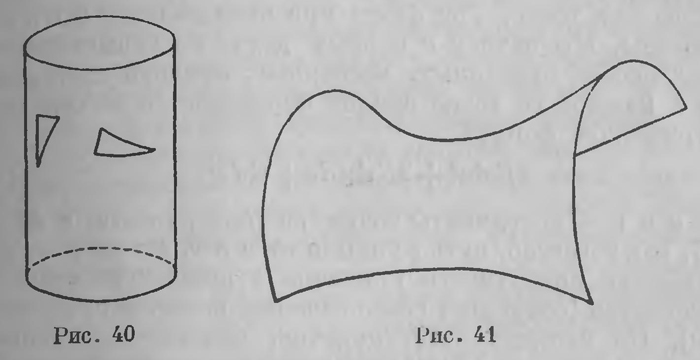
Если с этой точки зрения подойти к другим поверхностям, если искать поверхности, на которых возможно наложение именно в этом смысле слова (при помощи передвижения, сопровождаемого изгибанием), то число поверхностей, на которых это возможно, значительно возрастает. И, что для нас важнее всего, как показал Бельтрами, в обыкновенном (евклидовом) пространстве существуют поверхности, которые в этом смысле слова несут на себе двумерную геометрию (планиметрию) Лобачевского. Части такой поверхности имеют как бы седлообразный вид: они в одном направлении обращены, скажем, вверх (как седло по хребту лошади), а в перпендикулярном направлении — вниз (как седло поперек лошади) (рис. 41). Бельтрами назвал такие поверхности псевдосферическими. Все соотношения плоской геометрии Лобачевского, Уравнения, связывающие стороны и углы геодезического треугольника, связь между радиусом и длиной окружности, ее площадью и т. п., здесь выполняются в точности, совершенно так же, как это было предусмотрено планиметрией Лобачевского. Каждый, кто был в этом отношении заражен скепсисом, мог это проверить прямым измерением на многочисленных моделях таких поверхностей. Планиметрия Лобачевского получила осуществление на реальных образах, фантазия обратилась в действительность. Читатель обладающий некоторым математическим образованием, пожелает, конечно, получить, об этих поверхностях более четкие сведения. Ему достаточно будет для этого иметь ясное представление о так называемой кривизне (точнее, полной кривизне) поверхности в заданной на ной точке. Три факта при этом должны быть ему известны. Мы начнем с первых двух, по существу тесно между собой связанных. Во-первых, кривизна поверхности в каждой ее точке вполне определяется ее основной метрической формой. Е du2 + 2 F du dv+G dv2, (42) где u и v — координаты точки на поверхности, а Е, F и G, как известно, суть функции от u и v. Во-вторых, при изгибании поверхности кривизна в каждой ее точке не изменяется (сохраняет свое значение, остается инвариантной). По существу это, конечно, вытекает из первого факта, потому что изгибание поверхности математически тем и определяется, что коэффициенты Е, F, G при той же координации сохраняют свои значения, а вместе с тем сохраняет свое значение и кривизна поверхности в каждой ее точке. Предположим теперь, что поверхность допускает движения в самой себе, хотя бы путем изгибания, притом такие движения, что каждая точка поверхности может быть совмещена с любой другой ее точкой. Положим, что при некотором таком передвижении поверхности в самой себе точка М совместится с точкой М'. Так как кривизна в каждой точке передвигаемой поверхности сохранит свое значение, то она имеет в точке М’ тоже значение, что и в точке М. Если свобода передвижения на поверхности такова, что каждая ее точка может быть приведена в совмещение с любой другой точкой, то отсюда следует, что такая поверхность должна иметь во всех своих точках одну и ту же кривизну: это должна быть поверхность постоянной кривизны. Эта кривизна может иметь положительное значение, если в каждой точке все плоские сечения поверхности обращены в одну и ту же сторону от касательной плоскости (как это имеет место С овальной поверхности), или отрицательное значение, если эти сечения обращены частью в одну, частью в другую сторону (как это имеет место на седлообразной поверхности); она может иметь также нулевое значение (цилиндр, конус, всякая поверхность, развертывающаяся на плоскость). Замечательно, однако, что [постоянство кривизны составляет не только необходимое, но и достаточное условие того, чтобы поверхность допускала скольжение по самой себе хотя бы путем изгибания: всякая поверхность постоянной кривизны может передвигаться в самой себе с тремя степенями свободы, как это имеет место на плоскости и на сфере. Отсюда явно вытекает, что каждая поверхность постоянной кривизны допускает свою внутреннюю геометрию, устанавливаемую методом наложения. Из этого именно факта Бельтрами и исходил. Совершенно ясно, что в нашем обыкновенном (евклидовом) пространстве поверхности нулевой кривизны, т. е. такой же кривизны, какую во всех своих точках имеет (евклидова) плоскость,— поверхности, развертывающиеся на плоскость, несут на себе геометрию (планиметрию) Евклида; поверхности постоянной положительной кривизны путем изгибания развертываются на сферу такой же кривизны; они несут на себе сферическую геометрию. Какова же геометрия поверхности постоянной отрицательной кривизны? Бельтрами обнаружил, что на этих поверхностях имеет место двумерная геометрия (планиметрия) Лобачевского. Какими средствами он это показал? Замысел очень простой. Представим себе поверхность, основная метрическая форма (25) и (25а) которой в некоторых координатах имеет тот же вид, что и на плоскости Лобачевского: 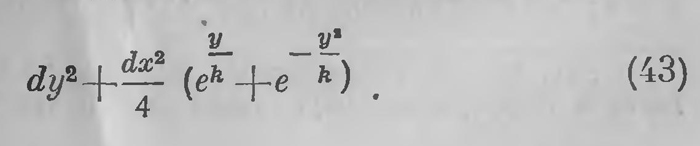
Если вычислить кривизну этой поверхности по этим коэффициентам основной формы, то она оказывается равной — 1/k2, где k — постоянная пространства. И обратно: на всякой поверхности, имеющей кривизну — 1/k2, основная метрическая форма в надлежащих координатах может быть приведена к виду (43). Иначе говоря, поверхность постоянной отрицательной кривизны имеет ту же основную метрическую форму, что и плоскость в геометрии Лобачевского. Теперь остается учесть третий факт, заключающийся в том, что основной метрической формой поверхности вполне определяется внутренняя ее геометрия. Так как поверхность постоянной отрицательной кривизны имеет ту же основную метрическую форму, что и плоскость Лобачевского, то она всегда несет на себе геометрию (планиметрию) Лобачевского. Как уже было сказано, Бельтрами назвал поверхности постоянной отрицательной кривизны псевдосферическими. Его замечательное открытие можно поэтому формулировать так: на всякой псевдосферической поверхности осуществляется геометрия Лобачевского. Впечатление, произведенное этим открытием, было громадно. Поражало главным образом то, что внутреннее усмотрение Лобачевского — можно сказать, чутье гениального геометра,— через фантастическую, на первый взгляд, гипотезу, через тонкие логические рассуждения, через сложные аналитические вычисления привело к неожиданной реальной действительности, которой не предусматривал сам автор. Теория здесь в «чистой математике» предвосхитила опыт. Существует бесчисленное множество псевдосферических поверхностей. Некоторые простейшие из них изображены на рис. 42. Особое место среди них занимает поверхность, которую просто называют псевдосферой; она изображена на рис. 431. Это поверхность, которая образуется вращением трактриссы вокруг своей директрисы2. Все эти поверхности были конкретно осуществлены,— точнее, были изготовлены модели их, и все результаты измерений, как этого требовала теория, конечно, совпадали, с предсказаниями плоской геометрии Лобачевского. 
Сомнения в логической правильности геометрии Лобачевского. казалось бы, должны были исчезнуть: то, что конкретно, материально осуществляется, не может содержать в себе логического противоречия, не может быть абсурдом. Вопрос, вызвавший сомнения, казалось, был решен, но высоки требования математика к каждому утверждению, которое он признает строго обоснованным. Здесь все же возникают сомнения, которые могли у читателя появиться еще раньше. Мы говорили выше, что геометрия круглого цилиндра совпадает с геометрией евклидовой плоскости. Но ведь на круглом цилиндре параллели суть геодезические линии; на нем, таким образом, имеются замкнутые, конечные геодезические. Между тем на евклидовой плоскости все прямые бесконечны, неограниченно простираются в обе стороны. Полного совпадения геометрии круглого цилиндра с геометрией евклидовой плоскости, таким образом, нет. Как же выразить точно то совпадение, которое действительно имеет место? Это отнюдь не трудно сделать. Дело заключается в том, что на круглом цилиндре евклидова геометрия осуществляется только локально. 
Это нужно понимать следующим образом. Разрезав круглую цилиндрическую поверхность по образующей, мы можем развернуть ее на плоскость; но она развернется, конечно, не на всю плоскость, а только на полосу, содержащуюся между двумя параллельными прямыми. И то, что происходит внутри этой полосы, вполне осуществляется на цилиндрической поверхности; то же, что происходит вне этой полосы, на цилиндр непосредственно не переносится. В этом заключается локальное (местное) совпадение геометрии цилиндра и плоскости. То же самое происходит и на псевдосфере: она не отображает всей плоскости Лобачевского, ее геометрия только локально совпадает с геометрией плоскости. Поэтому отображение неевклидовой плоскости на псевдосфере не доказывает со всей необходимой точностью, что планиметрия Лобачевского полностью на всем протяжении плоскости свободна от противоречий. Это возражение отпало бы, если бы была найдена такая псевдосферическая поверхность, на которой плоскость Лобачевского отображалась бы целиком. Что стоит на пути этого? Вглядываясь в 41—43 различных псевдосферических поверхностей, видим, что па каждой из них имеются либо конические точки, либо ребра, вообще особенные точки или линии. Поэтому, чтобы найти такую псевдосферическую поверхность, на которой плоскость Лобачевского отображалась бы целиком, нужно прежде всего разыскать псевдосферическую поверхность, которая не имеет никаких особенных точек. На этом было сосредоточено внимание многих геометров в течение почти четверти века. Но в 1901 г. Гильберту удалось обнаружить, что таких поверхностей вовсе не существует3. Прекрасный замысел Бельтрами далеко продвинул решение вопроса о непротиворечивости неевклидовой геометрии, но все еще не довел его до конца. Мемуар, в котором были изложены идеи Бельтрами, носил название «Опыт интерпретации неевклидовой геометрии»4. Помимо того значения, которое эта работа имела в деле признания неевклидовой геометрии, она сыграла еще одну весьма важную роль. В терминологии Бельтрами его результат выражался так: псевдосферическая поверхность является «интерпретацией» неевклидовой геометрии; мы теперь говорим — частичной, локальной ее интерпретацией. Была уяснена мысль, что одна и та же геометрическая система допускает различные, даже многообразные интерпретации, различные формы осуществления. Это был чрезвычайно важный шаг вперед в деле выяснения сущности и значения геометрии. Задача о непротиворечивости теперь заключалась в том, чтобы найти такую интерпретацию, которая осуществляла бы геометрию Лобачевского целиком, и притом не только в плоскости, но и в трехмерном пространстве. Это было выполнено; идеи трех замечательных геометров, объединенные в один замысел, привели к окончательному решению задачи. Геометры эти — Евгений Бельтрами, Бернгард Риман и Феликс Клейн. В 1854 г. Риман, имя которого хорошо известно всякому, кто стоит близко к математике, вступил доцентом в профессорскую коллегию Геттингенского университета. Для этого он должен был прочесть в общем собрании факультета пробную лекцию. Следуя принятому обычаю, он представил на усмотрение факультета три темы, из которых Гаусс выбрал третью, носившую название «О гипотезах, лежащих в основании геометрии». При составлении этой лекции Риман в качестве слушателя явно имел в виду главным образом самого Гаусса, и потому лекция была составлена очень сжато; это скорее конспект, наметки ряда глубоких идей, нежели готовая к печати работа. Именно поэтому Риман ее не опубликовал, очевидно имея в виду ее развить. Но он не успел это сделать. Дедекинд извлек рукопись уже из наследия Римана и опубликовал ее в 1866 г. Идеи, изложенные в этой работе, имеют тесное соприкосновение с работами Лобачевского. Риман начинает с установления понятия о «многообразии (Mannigfaltigkeit) как о совокупности элементов — объектов, выделенных, включенных в его состав определенными признаками. В настоящее время термину «многообразие» предпочитают другой: по почину Кантора его называют множеством. Это очень широкое понятие: всякая совокупность конкретных или абстрактных объектов, всякий коллектив вещей, понятий, идей представляет собой множество. Риман изучает множества особой категории, именно такие, в каждом из которых элемент может быть определен несколькими числовыми заданиями или, просто говоря, несколькими числами; количество этих чисел характерно для множества. Если элемент множества определяется п числами, то говорят, что оно имеет n измерений. Плоскость есть множество, элемент которого (точка) определяется двумя числовыми заданиями (двумя ее координатами) — это есть двумерное множество. В таком же смысле сферическая, цилиндрическая, да и всякая вообще поверхность может быть рассматриваема как двумерное множество точек. Связка лучей в пространстве, выходящих из одной точки, также есть двумерное множество, потому что элемент этого множества определяется двумя числовыми заданиями (в терминах, принятых в астрономии: высотой и азимутом); совокупность всех прямых на плоскости также есть двумерное множество. Каждая точка пространства определяется тремя числовыми заданиями (тремя координатами); пространство в обычном значении этого слова есть трехмерное множество точек; как обычно говорят, пространство имеет три измерения. Совокупность всех прямых в пространстве есть четырехмерное множество. В самом деле, зафиксируем какую-нибудь плоскость Q; прямая в пространстве определяется двумя координатами ее «следа» на плоскости Q, т. е. точки М, в которой она встречает плоскость Q, и двумя числами, которыми она определяется в связке прямых, выходящих из точки М. Совокупность всех окружностей на плоскости есть множество трех измерений; каждый ее элемент — окружность — определяется координатами центра и радиусом; совокупность всех сфер в пространстве есть множество четырех измерений. Совокупность всех эллипсов на плоскости есть множество пяти измерений. Но многообразие не должно быть непременно составлено из элементов обыкновенного геометрического типа, в обычном понимании этого слова. Гельмгольц, например, стоял на точке зрения, принятой в его время, что все цвета могут быть составлены из трех основных цветов, взятых в различных количествах. С его точки зрения, совокупность всех цветов есть трехмерное множество. Представим себе рой корпускул — частиц, несущихся в пространстве. В каждый момент элемент этого роя характеризуется тремя координатами точки, в которой он находится, а в течение времени — еще четвертым числовым заданием, указанием времени. Сплошной рой несущихся частиц в пространстве и во времени представляет собой четырехмерное множество. Мы остановились подробно на этом понятии потому, что оно имеет основное значение, играет в настоящее время огромную роль как в математике, так и в ее приложениях. Основной замысел Римана заключается в том, что геометрия вовсе не представляет собой, так сказать, исключительного достояния множества точек — двумерного (поверхности) или трехмерного (пространства). Можно строить геометрию прямых, геометрию кругов, шаров; но можно идти гораздо дальше, можно строить геометрию множества цветов, геометрию роя корпускул, материальных частиц. Если говорить об измерительной геометрии, то прежде всего необходимо установить исходный принцип для производства измерений в различных множествах; измерительную (метрическую) геометрию Риман именно и имел в виду. При такой широкой постановке вопроса, при таком расширении задачи геометрии возникает вопрос о том, как понимать измерение в любом множестве, как его производить, какое «мероопределение» в нем установить. Если не указать для этого общего принципа, то перспективы становятся совершенно расплывчатыми; не видно пути, по которому должно идти проникновение геометрии в другие множества. Риман это хорошо понимал. Центр тяжести его замысла, его главная заслуга в том именно и заключается, что он дал основной, исходный принцип для производства измерений в множествах, представляющих собой далеко идущее обобщение тех точечных многообразий, для которых была построена классическая геометрия. Замысел Римана заключается в следующем. Вся внутренняя геометрия поверхности, как мы знаем, развертывается из основной ее метрической формы (42). Это определенная положительная форма,— она на всей поверхности имеет положительные значения, каковы бы ни были значения дифференциалов du и dv. Риман принимает, что квадрат числа, выражающего удаление двух бесконечно близких элементов множества, всегда выражается определенной положительной квадратичной форой от дифференциалов координат. Подробнее: пусть х1, х2, х3,..., хn будут координаты какого-либо элемента; следуя Риману, будем говорить: какой-либо точки множества. Пусть х1 + dх1, х2 + dх2, х3 + dх3,..., хn+ dхn будут координаты бесконечно близкой точки; за расстояние между этими двумя точками (за удаление этих двух бесконечно близких элементов) Риман принимает число ds, квадрат которого выражается формулой 
это есть сумма членов вида gijdxidxj, квадратичная форма, коэффициенты которой gij зависят от координат х1, х2, х3,..., хn; форма определенная положительная, т. е. имеющая всегда — во всякой точке х1, х2,..., хn и при всех значениях дифференциалов — положительное значение. Может быть, будет правильно сказать, что Риман ставит своей целью изучать такого рода множества, в которых возможно и целесообразно установить понятие об удалении двух элементов при помощи формулы (44); это есть так называемое риманово мероопределение. Подобно тому как геометрию поверхности выводят из ее основной метрической формы, Риман строит геометрию множества из его основной формы. Внутри изучаемого множества n измерений могут проходить «подмножества» меньшего числа измерений, в том числе подмножества одного измерения, которые Риман называет линиями. Совершенно так же, как на поверхности, определяются геодезические линии множества, в котором установлено мероопределение (44). Во всяком таком множестве устанавливаются методы измерения длин, площадей и объемов различных размерностей. Множество с установленной в нем римановой метрикой принято называть римановым пространством, а его геометрию, в этом порядке идей развернутую,— римановой геометрией5 в широком значении этого слова. Термин «риманово пространство», имеющий чисто условное, но вполне конкретное значение, вызывал немало недоразумений. Забывали о том, что это наименование присвоено различного рода множествам, и соединяли с ним идеалистические, фантастические представления, связывали их с обыкновенным пространством. Нужно хорошо уяснить себе, что никакой мистики здесь нет, что риманово пространство есть любое множество, в котором установлено риманово мероопределение, а вместе с тем своеобразная риманова геометрия. С большим искусством Риман устанавливает понятие о кривизне в каждой точке пространства в этом широком его понимании. Дать здесь точные сведения о том, как это делается, мы не имеем возможности. Ограничимся только указанием, что кривизна в римановой геометрии устанавливается аналогично тому, как это делается на поверхности, с той, однако, разницей, что кривизна присваивается многообразию не только в определенной его точке, а в различных площадках, через эту точку проходящих. Это до некоторой степени можно себе уяснить, сравнивая с тем, что в неизотропной среде упругое напряжение в каждой точке различно в различных направлениях площадки, на которую оно действует. Установив эти общие понятия, Риман, естественно, ставит себе вопрос: каковы самые простые множества, несущие установленную им геометрию? Очень элементарные соображения обнаруживают, что наиболее простыми нужно считать те пространства, которые в каждой точке имеют одну и ту же кривизну во всех направлениях. Весьма замечательно, что при этих условиях кривизна не меняется от точки к точке, это — пространства постоянной кривизны. Такие пространства естественно разбиваются на три категории: пространства постоянной положительной кривизны, их геометрию принято называть эллиптической; пространства постоянной отрицательной кривизны, их геометрию называют гиперболической; наконец, пространства нулевой кривизны, их геометрию называют параболической. Для большей определенности ограничимся в дальнейшем пространствами (многообразиями, множествами) трех и двух измерений. Читатель, вероятно, догадывается, что параболическая геометрия — геометрия пространства нулевой кривизны — есть геометрия Евклида; гиперболическая геометрия есть не что иное как геометрия Лобачевского. Геометрию, созданную Лобачевским, в настоящее время так и называют гиперболической геометрией; говорят о гиперболической геометрии плоскости и пространства. Что же представляет собой эллиптическая геометрия? Для двумерной эллиптической геометрии ответ совершенно ясный: это геометрия сферы (с небольшой модификацией, на которой мы не будем здесь останавливаться), но и в трехмерной эллиптической геометрии все прямые (геодезические линии) — замкнутые, имеют конечную, и притом одну и ту же, длину; всякие две плоскости пересекаются, так же как и всякие две прямые на плоскости. Эллиптическая геометрия — это геометрия множества конечных размеров, конечного пространства. Можно сказать: как над геометрией Евклида надстроились геометрии Лобачевского и Римана, гиперболическая и эллиптическая, так над ними теперь поднялась геометрия Римана в широком смысле этого слова. Эволюция идет и дальше, охватывая все более разнообразные множества, подчиняя геометрии все большее число своеобразных конкретных, иногда чисто материальных коллективов. Возвратимся к работе Бельтрами. Он строил аналитически геометрию псевдосферы, но ведь это была в то же время, хотя бы и локально, гиперболическая геометрия, Двумерная геометрия Лобачевского. Бельтрами, естественно, прежде всего выводит уравнение геодезической линии — прямой в гиперболической плоскости. Это уравнение мы уже привели выше; в декартовых координатах, как таковые определены на стр. 226, оно имеет В11Д (23) или (23а). Но Бельтрами оперирует другими координатами, на которые уравнения (23) или (23а) естественно наводят. Положим X = k cos П(х), Y = k sin П(х) cos (у) = k cos (у'), (45) где k — постоянная гиперболического пространства. В координатах X, Y уравнение прямой ((23), стр. 229) принимает простой вид X cos ω + Y sin ω = k cos П (p), (46) становится линейным. Координаты X и Y теперь обыкновенно называют бельтрамиевыми координатами. 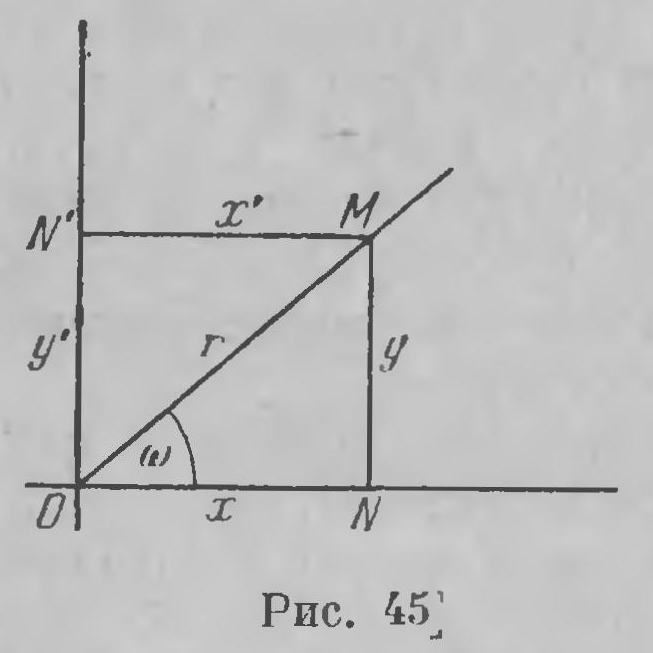
Можно сказать: бельтрамиевы координаты на гиперболической плоскости — это такие координаты, в которых прямая выражается линейным уравнением. Подойдем к ним геометрически. Возвратимся к рис. 21, который мы повторяем здесь с небольшой модификацией (рис. 45); здесь х и у' (а не у) суть проекции радиуса-вектора на оси ОХ и ОУ ортогональных координат. Если длину радиуса-вектора обозначим через r, то по теореме косинусов (11е) (стр. 201) из прямоугольных треугольников MON и MON' имеем: X = cos П (r) cos ω, Y = k cos П (r) sin ω. (47) Эти уравнения отличаются от формул преобразования полярных координат в декартовы в евклидовой плоскости только тем, что радиус-вектор r заменен через k cos П(r); при малых значениях r формулы (47) (см. равенство (16а) стр. 222) совпадают с этими формулами преобразования. Может быть, было бы правильнее рассматривать X и как гиперболический аналог декартовых координат; сохраним, однако, за ними установившееся название бельпрамиевых координат. Бельтрами пришел к ним своеобразным путем. Мы, к сожалению, останавливаться на этом не можем, так как должны уделить место другим соображениям. Уравнения преобразования (47) дают Х2+Y2 = k2 cos2П(r) < k2. (48) Это значит, что бельтрамиевы координаты всякой точки гиперболической плоскости удовлетворяют неравенству Х2+Y2< k2. (49) Обратно, если заданы числа X и Y, удовлетворяющие этому неравенству, то из уравнения (48) получаем cos П(r), вместе с тем и r, а при помощи уравнений (47) определим угол ω и точку М. Можно, таким образом, сказать, что числа X и Y действительно служат бельтрамиевыми координатами некоторой точки гиперболической плоскости в том и только в том случае, когда они удовлетворят неравенству (49). Прежде чем этим воспользоваться, остановимся еще на том случае, когда Х2+Y2< k2. (50) Уравнение (48) в этом случае дает cos П(r) = 1, П(r) =0, r = оо; если числа X и У связаны уравнением (50), то им соответствует бесконечно удаленная точка гиперболической плоскости. Теперь поступим следующим образом. Представим себе гиперболическую плоскость с бельтрамиевой координацией X, Y и евклидову плоскость с установленными в ней осями декартовых координат. Пусть М будет точка гиперболической плоскости (рис. 46) с бельтрамиевыми координатами X, Y; на евклидовой плоскости при установленной декартовой координации нанесем точку m, имеющую декартовы (рис. 46а) координаты X и Y. Мы можем смотреть на точку m как на изображение на евклидовой плоскости точки М гиперболической плоскости: ясно, что вся гиперболическая плоскость, все ее точки будут, таким образом, отображены на евклидовой плоскости. На последней построена карта, изображающая всю гиперболическую плоскость; на ней можно ясно видеть все, что происходит на гиперболической плоскости. Уравнение (50) на евклидовой плоскости выражает окружность радиуса к с центром в начале координат; неравенство (49) выражает, что каждая точка m, какую бы точку М гиперболической плоскости она ни изображала, падает внутрь этого «граничного» круга. Иначе говоря, вся гиперболическая плоскость отображается на круге евклидовой плоскости. 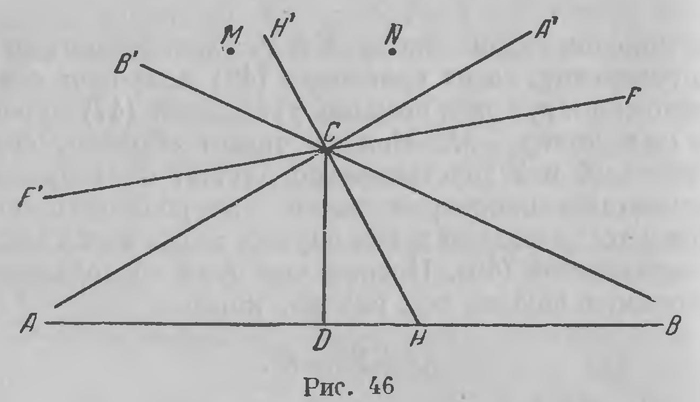
При этом точки, удовлетворяющие на карте уравнению (50), т. е. лежащие на окружности граничного круга, как мы видели, соответствуют бесконечно удаленным точкам гиперболической плоскости. Прямая гиперболической плоскости выражается в бельтрамиевых координатах линейным уравнением. Но линейным же уравнением в тех же координатах X, Y на евклидовой плоскости также выражается прямая на нашем круге — его хорда. Прямые гиперболической плоскости изображаются на карте хордами граничного круга; концы хорд отвечают бесконечно удаленным точкам гиперболической прямой. Теперь пусть ab будет какая-либо хорда граничного круга, АВ — соответствующая прямая на гиперболической плоскости, с — точка вне этой прямой, С — соответствующая точка гиперболической плоскости. Итак, с — точка, лежащая в нашем круге вне прямой ab; для скоторого упрощения возьмем ее сначала в центре круга. Прямым ab, са, сb соответствуют на гиперболической плоскости прямые АВ, СА и СВ; и так как точкам а и b соответствуют бесконечно удаленные точки, то СА и СВ суть прямые, параллельные АВ именно в том смысле, как это понимает Лобачевский. Прямые ch, проходящие внутри угла асb, пересекают хорду аb; им соответствуют на гиперболической плоскости прямые СН, пересекающие прямую АВ, сходящиеся с ней. Прямые сf, проходящие внутри 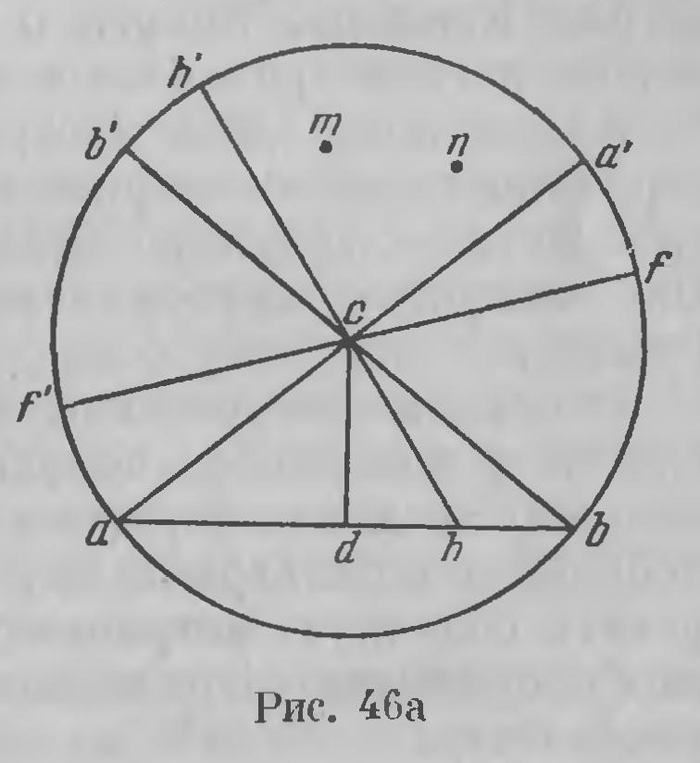
вертикальных углов bса' и асb', не встречают хорды аb; соответствующие им на гиперболической плоскости прямые CF расходятся с АВ. Сравнивая этот рисунок с рис. 8, видим, что построенная таким образом карта в точности воспроизводит все происходящее в гиперболической плоскости; здесь, на этом круге полностью осуществляется гиперболическая геометрия, она становится вполне доступной глазу, она совершенно утратила свой фантастический характер. Если за расстояние между двумя точками тип принимать число, выражающее расстояние MN соответствующих точек па гиперболической плоскости и совершенно аналогично измерять углы, то и все метрические соотношения гиперболической плоскости на этой карте выполняются полностью. Углу acd отвечает на гиперболической плоскости угол параллельности, соответствующий отрезку CD. Картина изменяется очень мало, если точку с взять не в центре круга, а в произвольной его точке; мы не можем здесь на этом останавливаться. На «основной» или «абсолютный» круг в описанной здесь схеме можно смотреть, как на интерпретацию гиперболической геометрии, полностью ее осуществляющую, нa этом круге можно отобразить, конечно, и всякую псевдосферическую поверхность, но только она отображается не на всем круге, а на части его; это, как мы знаем, составляет единственное слабое место интерпретации гиперболической геометрии при помощи псевдосферы. Интерпретация на бельтрамиевом круге этого дефекта не имеет; она осуществляет двумерную гиперболическую геометрию полностью. Геометрия Лобачевского воспроизведена в евклидовой плоскости и потому в отношении логической правильности она вызывает не больше сомнений, чем геометрия Евклида. Вопрос о непротиворечивости гиперболической геометрии был в этом смысле разрешен. Изложенное здесь построение — воспроизведение гиперболической геометрии внутри круга на евклидовой плоскости — задумано Бельтрами и завершено Клейном. Оно получает другое освещение с точки зрения идей Римана. Основная метрическая форма гиперболической плоскости в декартовых координатах имеет вид (43). Уравнения (45) дают формулы преобразования декартовых координат в бельтрамиевы. С их помощью нетрудно выразить основную метрическую форму (43) в бельтрамиевых координатах. Это вычисление приводит к следующему результату: 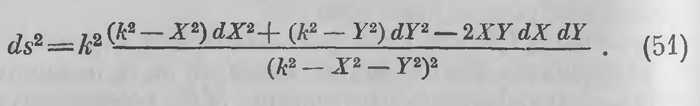
Становясь теперь на точку зрения Римана, будем строить геометрию в следующем порядке идей. Рассмотрим множество точек, расположенных в евклидовой плоскости внутри некоторого круга радиуса к. Это множество будет тем пространством, внутри которого мы будем строить геометрию. Отнесем этот круг к ортогональным декартовым координатам (XY), принимая центр за. начало. Следуя общему замыслу Римана, определим в этом множестве элемент длины формой (51); она будет иметь положительное значение во всякой точке круга. Геометрия этого множества при основной форме (51) есть двумерная гиперболическая геометрия. Подойдем ли мы к этой инрпретации с точки зрения Бельтрами и Клейна, или точки зрения Римана,— мы во всяком случае получаем безукоризненную интерпретацию двумерной гиперболической геометрии. Совершенно ясно, что таким же образом трехмерное гиперболическое пространство с его геометрией может быть отображено на шаре; мы получаем таким путем безукоризненную интерпретацию трехмерной геометрии Лобачевского. Идея интерпретации геометрии, сознание возможности ее осуществления в различных множествах, получили широкое развитие. Ближайшие годы принесли с собой различные интерпретации как евклидовой, так и неевклидовой геометрии. На цилиндрической поверхности осуществляется двумерная геометрия Евклида; на круглом цилиндре — только локально, на параболическом цилиндре полностью; локально она осуществляется на всякой поверхности, развертывающейся на плоскость. Но существуют и различные другие интерпретации двумерной евклидовой геометрии; остановимся на одной из них, чрезвычайно остроумной, которая ведет начало от Пуанкаре; мы ее здесь вкратце изложим. В евклидовой плоскости выделим произвольную точку О и изымем ее из этой плоскости. Иными словами, будем рассматривать множество, состоящее из всех точек плоскости кроме точки О. Это множество будем называть плоскостью Пуанкаре. Мы будем строить геометрию в плоскости Пуанкаре. Элементами этого множества, его точками, будут служить точки этой плоскости. Но под "прямыми" мы будем теперь разуметь не обыкновенные прямые, а окружности, проходящие через точку О (рис. 47); в число их мы включим и прямые, проходящие через точку О, как окружности бесконечно большого радиуса. Очень любопытно, что геометрия, построенная на этих началах, есть геометрия Евклида. В самом деле, через каждые две "точки" проходит одна—и только одна— "прямая"6: если точки А и В не лежат на одной обыкновенной прямой с точкой О, то этой "прямой" служит окружность, проходящая через точки А, В и О; если же точки А и В лежат на одной обыкновенной прямой с точкой О, то этой "прямой" будет служить обыкновенная прямая АВ. Две "прямые" обычно пересекаются водной — и только в одной — "точке", ибо две окружности, проходящие через точку О, помимо нее имеют еще одну — и только одну — общую точку. Исключение представляет только тот случай, когда эти две окружности касаются в точке 0; тогда соответствующие "прямые" параллельны. 
Прямолинейный отрезок (дугу круга) можно продолжить в обе стороны, и притом продолжить неограниченно, поскольку точка О нам недоступна (это бесконечно удаленная точка плоскости). Рассмотрим теперь "прямую" и "точку" С (рис. 48), лежащую вне ее. Можно ли через точку С провести прямую, не встречающую данной прямой, и если возможно, то существует ли только одна такая прямая или больше? Построение такой прямой сводится к тому, чтобы через точку С провести окружность, касающуюся данной окружности в точке О. Элементарные соображения обнаруживают, что существует одна — и только одна — такая окружность. Мы видим, таким образом, что в плоскости Пуанкаре осуществляются постулаты евклидовой геометрии; в ней поэтому имеет место евклидова геометрия. Мы пришли к своеобразной ее интерпретации. Конечно, чтобы этот факт установить с полной точностью, нужен еще ряд дополнительных соображений. Нужно установить в этой геометрии мероопределение, нужно прежде всего установить, как измеряются длины и углы. Под узлом между двумя прямыми разумеют обыкновенный угол между соответствующими окружностями. Расстояние между двумя точками выражается сложнее: мы не можем изложить здесь все эти соображения. 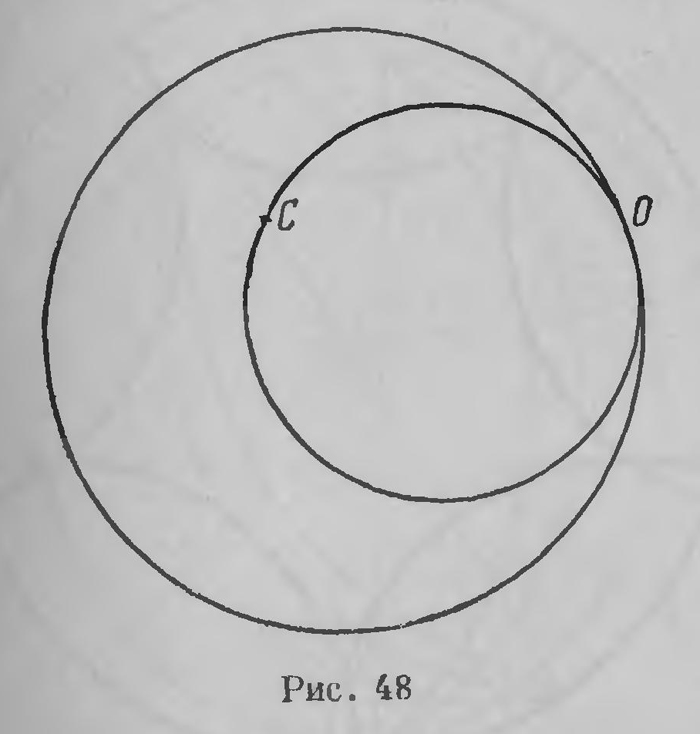
Совокупность окружностей, проходящих через одну точку (рис. 47), образует так называемую связку окружностей .Схема Пуанкаре воспроизводит параболическую геометрию в связке окружностей. Связку рассмотренного типа называют параболической связкой. Мы можем, таким образом, сказать, что в параболической связке осуществляется евклидова геометрия; иначе говоря, Пуанкаре указал интерпретацию евклидовой геометрии в параболической связке окружностей. Но связкой называют также множество окружностей Другого типа. Так, гиперболической связкой называют совокупность окружностей, секущих ортогонально одну и ту же (основную) окружность (рис. 49а); эллиптической связкой называют совокупность окружностей, секущих основную окружность диаметрально, т. е. в концах ее диаметра (рис. 496). 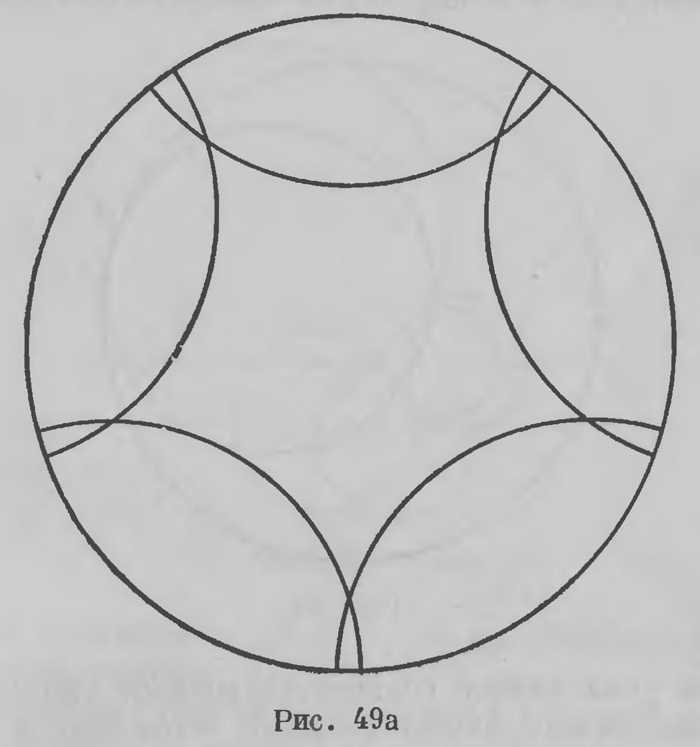
Аналогично тому, как в параболической связке окружностей устанавливается евклидова (параболическая) геометрия, в гиперболической связке устанавливается гиперболическая, а в эллиптической связке — эллиптическая геометрия. Конечно, надлежащее выяснение этого требует еще много дополнительных соображений, которых мы здесь излагать не можем. Но основная мысль, мы полагаем, выяснена достаточно отчетливо: в различных связках окружностей можно построить совершенные интерпретации как евклидовой, так и обоих типов неевклидовой геометрии. В пространстве аналогом связок окружностей служат связки сфер, и в этих связках можно построить совершенные интерпретации трехмерной геометрии, евклидовой п неевклидовой одного и другого типа7. 1Рис. 42 и 43 заимствованы из книги Эйзенгарта «Введение в дифференциальную геометрию в цензорном изложении» 2Пол трактриссой, по инициативе Лейбница, разумеют кривую (рис. 44), которую описывает материальная точка, влекомая нитью постоянной длины r, другой конец которой скользит по прямой - ее директриссе, касательная MN в каждой точке, отсчитываемая от этой точки до директриссы, сохраняет таким образом постоянную длину. Число r называется параметром трактриссы. 3D. Hilbert. Ueber Flachen von constanter Gausscher ivrummung. Transactions of the American Math. Soc., 2, 1901. См. также D. Hilbert. Grundlagen der Geometrie. Leipzig — Berlin. VII Auflang , Anhang V. 4E. Beltrami. Saggio di interpretazione della geometria non-euclidea. Giornale di matematiche, 6, 1868. Мемуар переведен на русский язык под названием «Опыт объяснения неевклидовой геометрии»; он помещен в казанском сборнике «Об основаниях геометрии». 5Подробнее об этом см. В. Ф. Каган. Геометрические идеи имана и их современное развитие. М. - Л., 1933. 6Мы пользуемся кавычками для обозначения термина в том иачении, которое он имеет в интерпретации Пуанкаре. 7Подробную разработку этих идей читатель может найти во И томе «Энциклопедии элементарной математики» Вебера и Вельштейна. Одесса, 1914. |
загрузка...
