XIV. Первые работы Лобачевского по неевклидовой геометрии

Читая начинающим студентам курс элементарной математики, в частности, геометрии, Лобачевский заинтересовался теорией параллельных линий. Он не избежал общей участи тех, кто занимался этим вопросом, он попытался доказать V постулат. Сохранилась запись одного из его слушателей (М. Темникова), содержащая доказательство, которое Лобачевский излагал на своих лекциях. Доказательство не лишено, конечно, остроумия; но оно основано на неправильности чертежа, которую Лобачевский скоро обнаружил; мы его не воспроизводим¹. Курс этот Лобачевский читал в 1815 г. и, следовательно, тогда он не имел еще определенной точки зрения на этот вопрос. Ближайшие годы были, очевидно, годами настойчивого размышления об этом предмете. «Геометрия», представленная Лобачевским к напечатанию в 1823 г., свидетельствует о том, каковы были в то время его взгляды на этот вопрос.

Во-первых, совершенно ясно, что Лобачевский отдавал себе полный отчет и том расщеплении геометрии, которое производит постулат о параллельных линиях. Более того, в свете этого, как указано выше, становится понятным то необычное распределение материала, которое вызывало такое недоумение у Фусса: Лобачевский в первых пяти главах отобрал тот материал, который не зависит от постулата о параллельных, который принадлежит абсолютной геометрии. «Геометрия» Лобачевского — это первое сочинение в мировой литературе, в котором абсолютная геометрия полностью выделена, и этим объясняется фузионизм, отнюдь не преследующий здесь педагогических целей; он имеет в виду отделить, изложить в первую очередь не только планиметрические, но и стереометрические предложения, которые доказываются без помощи V постулата. Фусс был от этого чрезвычайно далек, и совершенно естественно, что расположение материала вызвало у него полное недоумение. Твердо стоя на своей метрической точке зрения, Лобачевский отдает себе ясный отчет в том, что измерение отрезков и градусное измерение углов от постулата не зависит, а измерение площадей, прежде всего прямолинейных фигур, коренным образом зависит от постулата. Вот почему, обращаясь к измерению прямоугольников, он начинает посвященную этому главу VI следующими словами:

«Измерение плоскостей основывается на том, что две линии сходятся, когда они стоят на третьей по одну сторону и когда одна перпендикул, а другая наклонена под острым углом, обращенным к перпендикулу. Линин АВ и CD [см. стр. 179] должны сходиться по достаточном продолжении, есть ли одна из них АВ перпендикулярна к ВС, а другая CD наклонена к ВС под острым углом С, обращенным к перпендикулу АВ. Строгого доказательства сей истины до сих пор не могли сыскать. Какие были даны могут назваться только пояснениями, но не заслуживают быть почтены в полном смысле математическими доказательствами» (см. факсимиле на стр. 179).

Лобачевский принимает таким образом постулат в лежандровой формулировке и отдает себе ясный отчет в том, что ни одно из предложенных доказательств его не может быть признано убедительным. В качестве лучшего из этих неудовлетворительных доказательств он приводит очень известное, несомненно остроумное доказательство- Л. Бертрана, которое основано на неправильном использовании бесконечно малых и бесконечно больших величин².

Итак, в «Геометрии», в этой книге Лобачевского, которая не была разрешена к печати, от которой были склонны отказать я даже некоторые авторы текущего столетия, впервые абсолютная геометрия была четко отделена от собственно евклидовой. Оставалось только обнаружить, что межа, проходящая между пятой и шестой главой «Геометрии», производит не механическое разделение геометрии на две части, что она служит точкой разветвления, что от нес разрастается новая геометрия в бесчисленных разновидностях, среди которых простейшей является собственно евклидова геометрия. Это было Лобачевским выполнено в следующие три года.

Путь, которым Лобачевский к этому пришел, заключался в следующем.

Факсимиле из рукописи Н. И. Лобачевского «Геометрия». 23-я страница, относящаяся к учению о параллельных линиях.

Подобно Лежандру, он, по-видимому, сначала пытался доказать постулат от противного. Самый постулат о параллельных он брал при этом в Плейферовой форме (стр. 167). Соответственно этому для доказательства от противного Лобачевский, сохраняя остальные аксиомы и постулаты Евклида, вместо постулата о параллельных, принимал, что через точку С, лежащую вне прямой АВ (рис. 8), в плоскости ABC проходит больше одной прямой, не встречающей АВ (прямые СЕ, CF, CG); можно было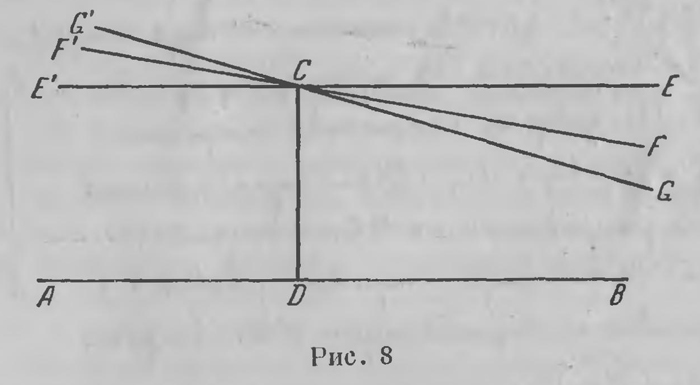

ожидать, что выводы из такого, на первый взгляд совершенно нелепого, допущения приведут к абсурду, к противоречию с абсолютной геометрией. Но тонкие выводы, которые Лобачевский мастерски проводил, к такому противоречию не приводили. Правда, его выводы находились в разительном противоречии с интуицией, с указаниями глаза; но не было никакого противоречия логического, не было противоречия с тем, что было доказано раньше. Напротив, выводы, последовательно проводимые, постепенно складывались в законченное гармоническое целое, которое Лобачевский назвал «воображаемой», Гаусс — «неевклидовой» геометрией, а мы теперь называем геометрией Лобачевского.

Как уже было указано выше, 11 (23) февраля 1826 г. Лобачевский сделал в заседании физико-математического факультета (отделения, как тогда чаще говорили) доклад, оформленный в то же время для печати под названием «Exposition succincte des principes de la Geometrie avec une demonstration rigoureuse du theoreme des paralleles». (Сжатое изложение начал геометрии со строгим доказательством теоремы о параллельных линиях.) В январе 1926 г., когда готовилось празднование столетнего юбилея открытия неевклидовой геометрии, профессором Н. И. Порфирьевым в архиве Казанского университета была найдена препроводительная бумага, с которой эта работа была представлена в факультет. Приводим ее содержание полностью.

«Препровождаю сочинение мое под названием: Exposition succincte des principes de la Geometrie avec une demonstration rigoureuse du theoreme des paralleles.

Желаю знать мнение о сем ученых, моих сотоварищей и есть ли оно будет выгодно, то прошу покорнейше представленное мною сочинение принять в составление ученых записок Физико-математического отделения, в каком намерении я и предпочел писать на французском языке, так как предполагалось записки издавать на сем языке, сделавшемся ныне общим между учеными.

Проф. Н. И. Лобачевгкий».

На этой бумаге вверху имеется отметка: «Получено 7-го февраля 1826 г.», а внизу написано: «слушано 1826 г. 11 февраля ст. I. Определено: Поручить рассмотреть сочинение гг. профессорам Симонову, Купферу и адъюнкту Брашману и мнение свое сообщить отделению».

Главную роль в этой комиссии несомненно должен был играть И. М. Симонов — астроном и математик. А. Я. Купфер (впоследствии академик) в то время занимал в Казанском университете кафедру химии, временно также физики. Н. Д. Брашман с марта 1825 г. состоял адъюнктом по кафедре математики; это был очень одаренный человек; позже он был приглашен профессором в Московский университет, во второй половине прошлого века он пользовался большим уважением в русских математических кругах³. Нужно, однако, сказать, что Симонов был вообще человеком недоброжелательным и к Лобачевскому, как увидим, относился очень сдержанно; от абстрактных вопросов математики он был далек. Еще более далек от них, конечно, был Купфер. Вопросы обоснования геометрии, к которым относилось исследование Лобачевского, были чужды трем членам комиссии. В работе Лобачевского они не разобрались. Может быть, это им и было очень трудно сделать, хотя тут же был живой автор, от которого можно было бы получить разъяснения. Но комиссия поступила иначе. Она отнеслась к работе Лобачевского отрицательно; сохранились прямые указания, что Брашман, например, выразился о ней в очень пренебрежительном тоне⁴. Однако комиссия решила «пощадить» товарища. Она не дала о работе никакого отзыва и в то время, по-видимому, не возвратила рукописи в факультет. Во всяком случае, в ближайших протоколах отделения никакого упоминания о ней нет; все старания разыскать ее в архивах к цели не привели: она считается безвозвратно утерянной. Но Л. Б. Модзалевскому удалось прочесть надпись на препроводительной бумаге Лобачевского, приведенной выше в тексте и в фотокопии. Она гласит, что дело «сдается в архив для хранения по постановлению Отделения от 13 июля 1834 г.»⁵ Но ни это постановление, ни протокол в архиве университета не обнаружены. Существеннее всего то, что Лобачевскому и на этот раз не удалось опубликовать свою работу.

При всем том мы имеем возможность довольно точно воспроизвести ее содержание. Через три года, в 1829 г., Лобачевский все же опубликовал в журнале «Казанский вестник», который рассматривался как орган университета, мемуар, носивший название «О началах геометрии». Примерно первая треть этой работы, как указывает сам Лобачевский, «извлечена самим сочинителем из рассуждения «Exposition succinete», читанного в заседании отделения 12 февраля 1826 г.»⁶.

Эта часть после некоторых вступительных рассуждений, о которых мы будем иметь случай говорить ниже, содержит изложение начал новой, созданной Лобачевским неевклидовой геометрии и заканчивается уравнениями, которые в этой геометрии связывают стороны и углы прямолинейного треугольника; все остальное добавлено позже. Этим в общих чертах устанавливается содержание работы «Exposition succincte». «Заглавие представленной Лобачевским рукописи («Exposition succinete»), — как правильно замечает А. П. Котельников во вступительной статье к мемуару «О началах геометрии»⁷,— возбуждает некоторое недоумение». Не совсем ясно, что подразумевал Лобачевский под словами «demonstration rigoureuse du theoreme des paralleles» (строгое доказательство теоремы о параллельных линиях). Во всяком случае, поскольку в ней содержались уже начала новой неевклидовой геометрии, не может подлежать сомнению, что речь идет не о новой попытке дать доказательство постулата о параллельных линиях, а о новой строгой постановке всего учения о параллельных линиях.

Ни мемуар «О началах геометрии», ни последовавшие за ним сочинения Лобачевского никем у нас поняты не были; напротив, они подвергались резкой критике, которую мы приводим в следующей главе. Лобачевский решил поэтому составить небольшое сочинение, которое содержало бы только начала открытой им новой геометрии, но было бы изложено в более доступной форме. Это и было им выполнено в 1840 г. Такое сочинение было им опубликовано в Берлине на немецком языке в виде отдельной брошюры под заглавием «Geometrische Untersuchurgen zur Theorie der Parallellinien»⁸ (Геометрические исследования по теории параллельных линий). Собственно это единственное сочинение, составленное Лобачевским так, что при некотором напряжении человек, владеющий общим математическим образованием и склонный вдумчиво отнестись к прочитанному, может вполне овладеть новыми идеями созданной им геометрии. Это один из лучших перлов мировой математической литературы. Именно по этому сочинению, правда, на четверть века позже, с идеями Лобачевского познакомился весь математический мир (см. главу XXVIII). «Геометрические исследования» заканчиваются теми же уравнениями, которыми, по указанию Лобачевского, заканчивалось рассуждение «Exposition succinеte». Не подлежит сомнению, что эта книга содержит тот же материал, который Лобачевский изложил в знаменательный день 11 (23) февраля 1826 г. и письменно в «Exposition succinеte», может быть, только в несущественной модификации. Мы постараемся поэтому в кратком очерке изложить содержание этого сочинения и тем попытаемся ввести читателя в круг идей Лобачевского. Конечно, для основательного их усвоения нужно изучить либо подлинные сочинения Лобачевского (в этом случае тоже лучше всего начать с «Геометрических исследований»⁹), либо те или иные позднейшие сочинения, посвященные этому предмету; список их указан в библиографическом указателе. Настоящий очерк претендует только на то, чтобы дать читателю общее представление об этих замечательных идеях и тем дать ему возможность хотя бы в некоторой степени ознакомиться с творчеством Лобачевского.

¹Оно изложено в приложении к изданию «Геометрии», выпущенному Казанским физико-математическим обществом (см. стр. 86). В этом приложении приводятся три доказательства постулата, но из них, как указал П. А. Широков, только первое действительно принадлежит Лобачевскому.
²Читатель на идет это доказательство и указанных выше (стр. 170) сочинениях. Оригинальное доказательство помещено в сочинении L. Bertrand. Developpement nouveau de la partie e1ementaire des matliematiqnes. Geneve, 1778. Более доступно второе издание этой книги, вышедшей под названием «Elements de geometric». Paris, 1812.
³Более подробные сведения об этих лицах см. в Биографическом словаре профессоров и преподавателей Казанского университета, т. I—II, К., 1904.
⁴См. воспоминания бывшего студента Казанского университета И. И. Михайлова. Л. Б. Модзалевский, Лобачевский, стр. 616.
⁵На фотокопии подпись ясно видна.
⁶Лобачевский ошибся, доклад состоялся не 12-го, а 11-го февраля.
⁷В т. I Полного собрания сочинении Н. И, Лобачевского.
⁸Berlin, Finke, 1840. Перевод его выпущен отдельным изданием (см. сноску на стр. 170).
⁹Именно поэтому мы здесь излагаем содержание этого сочинения, нарушая хронологическую последовательность работ Лгбачевского. По тем же основаниям этот мемуар помещен на первом месте в томе I «Полного собрания сочинений Лобачевского».

<<Назад Вперёд>>

Просмотров: 5524

загрузка...

Другие книги по данной тематике