XV. «Геометрические исследования по теории параллельных линий»

Сочинение «Геометрические исследования по теории параллельных линий» Лобачевский после краткого введения начинает перечислением 15 важнейших положений абсолютной геометрии, которыми ему необходимо пользоваться в дальнейшем изложении. Одни из этих положений представляют собой постулаты, другие — теоремы, во всяком случае все это — предложения (в широком смысле этого слова), которыми мы неизбежно пользуемся при построении абсолютной геометрии. Вслед за этим Лобачевский становится на путь, который приводит его к неевклидовой геометрии.

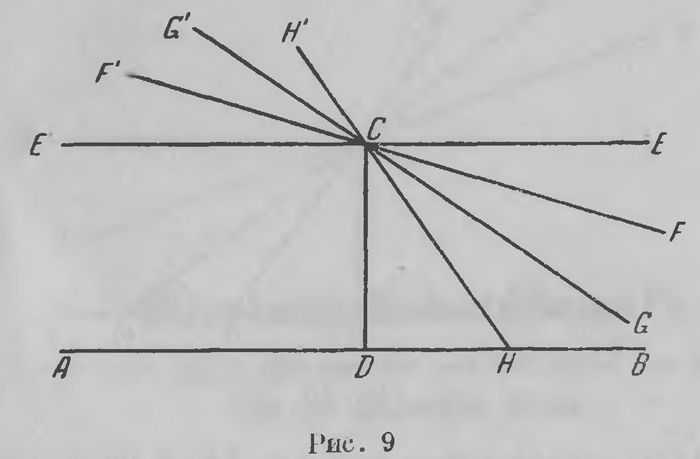
Обратимся к чертежу, которым мы уже собственно пользовались выше. Из точки С (рис. 9) опустим на прямую АВ перпендикуляр CD, а к нему в той же плоскости через точку С проведем еще перпендикуляр Е'СЕ (прямую часто будем обозначать тремя буквами, чтобы отметить два луча, из которых она состоит: СЕ и СЕ'). Допущение, которое делает Лобачевский в дополнение к абсолютной геометрии в соответствии с его установкой, заключается в том, что в той же плоскости АСВ через точку С, кроме прямой Е'СЕ (евклидовой параллели), проходит по крахщей мере еще одна прямая G'CG, также не встречающая прямой АВ. Отсюда ясно, что при таком допущении всякая прямая F'CF, проходящая через точку С между прямыми Е'СЕ и G'CG (т. е. внутри вертикальных углов ECG и E'CG'), также не встречает АВ. Допущение приводит, таким образом, к тому, что через точку С в той же плоскости проходит бесчисленное множество прямых, не встречающих прямой АВ. Если остановимся на прямых, проходящих в первом квадранте (т. е. в прямом угле ВСЕ), то они таким образом разбиваются на прямые вида Н'СН, встречающие прямую А В, и па прямые вида F'CF, ее не встречающие; первые (в квадранте I) расположены ближе к перпендикуляру CD, вторые ближе к СЕ.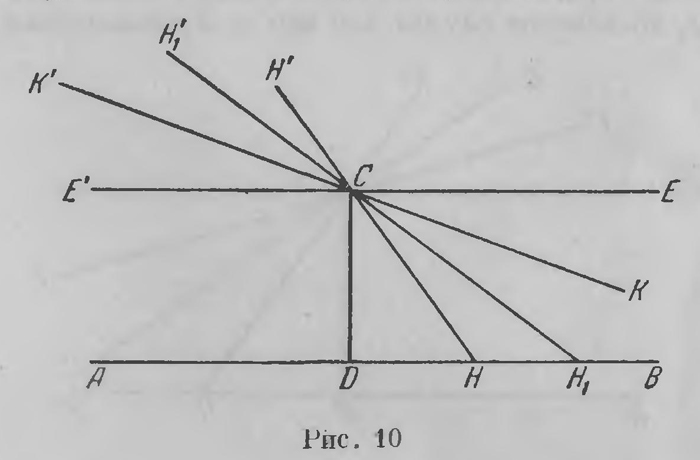

Ввиду непрерывности пучка отсюда следует, что в этих квадрантах должна существоватьпрямая, отделяющая прямые одной категории от прямых второй категории. Однако (рис. 10) последней встречающей прямой в этом пучке быть не может. В самом деле, какова бы пи была пересекающая прямая Н'СН, взяв точку Н₁ за точкой Н, получим прямую Н₁’СН₁, лежащую за Н'СН и все еще встречающую АВ. Поэтому граничная прямая К'СК будет первой прямой, не встречающей А В. Так как в IV квадранте естественно будет происходить то же, что и в I, то вся картина представится в таком виде, как это отчетливо изображено на рис. 11: здесь черными линиями изображены «старые» прямые, встречающие прямую АВ, красными — «новые» прямые, не встречающие АВ; синие линии изображают две прямые, отделяющие прямые встречающие от не встречающих. Эти две прямые Лобачевский называет параллельными АВ.

Титульный лист немецкого издания «Геометрических исследовали по теории параллельных линий».

Таким образом, термин прямая СК параллельна прямой АВ имеет у Лобачевского более узкое значение, чем в геометрии Евклида: он означает, что прямая СК не только не встречает прямой АВ, но в точке С с той или другой стороны отделяет прямые, встречающие прямую АВ от не встречающих ее; это паши синие прямые; красные не называются параллельными АВ.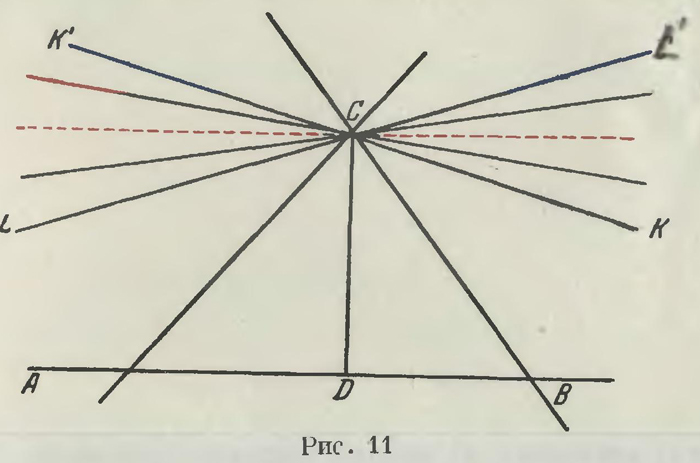

Воображая себе плоскость, в которой осуществляются допущения Лобачевского, называют ее плоскостью Лобачевского; в таком же смысле говорят о пространстве Лобачевского. Вместе с тем мы можем сказать, что в плоскости Лобачевского через точку С, лежащую вне прямой АВ, проходят две параллельные ей прямые (на рис. 11 К'СК и L'CL). Они образуют две пары вертикальных углов; прямые, проходящие внутри вертикальных углов KCL и К'СL', встречают АВ, по терминологии Лобачевского, сходятся с АВ, прямые же, проходящие внутри углов К'СL и КСL', по терминологии Лобачевского, расходятся с АВ. Если имеем две прямые АВ и CG, то вторая, выходя из любой своей точки С, либо сходится с АВ, либо параллельна ей, либо расходится с ней. При этом, если прямая CG в какой-либо своей точке С сходится с АВ (т. е., выходя из этой точки сходится с АВ), параллельна ей или расходится с ней, то те же функции, если можно так выразиться, она выполняет и во всякой другой своей точке С'. Подробнее это значит: если какая-либо прямая CG (рис. 12) в точке С расходится с АВ, то и в другой своей точке С' она с ней расходится; если в точке С она ей параллельна, то и во всякой другой своей точке С' она ей параллельна.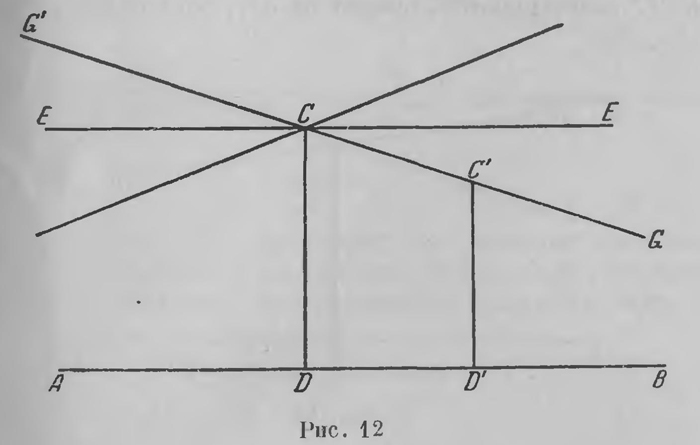

Это утверждение, конечно, требует обоснования, которого мы не можем здесь привести, но оно выполняется безукоризненно. Мы получаем, таким образом, возможность говорить просто: прямая CG сходится с АВ, параллельна ей, расходится с АВ (не относя параллелизма или расхождения к определенной точке С этой прямой). И это поведение одной прямой относительно другой, как оказывается, всегда взаимное. Ясно, что неевклидова параллель» СЕ теперь принадлежит к числу прямых, расходящихся с АВ.

Необходимо отметить еще один важный момент. Относительно параллели СК (рис. 13), образующей с перпендикуляром CD острый угол DCK со стороны DB, говорят, что она параллельна АВ в сторону АВ, тогда как вторая параллель CL параллельна ей в сторону ВА. При таком понимании параллелизма, как уже легко видеть, сохраняется основное свойство параллелей в евклидовой геометрии: две прямые, параллельные третьей в одну и ту же сторону, параллельны между собой в ту же сторону. В геометрии Евклида обе параллели к прямой сливаются в одну; вертикальные углы KCL и K'CL развертываются каждый в два прямых, смежные же с ними углы К'СL и KCL' свертываются, сходят на нет, обращаются в нуль.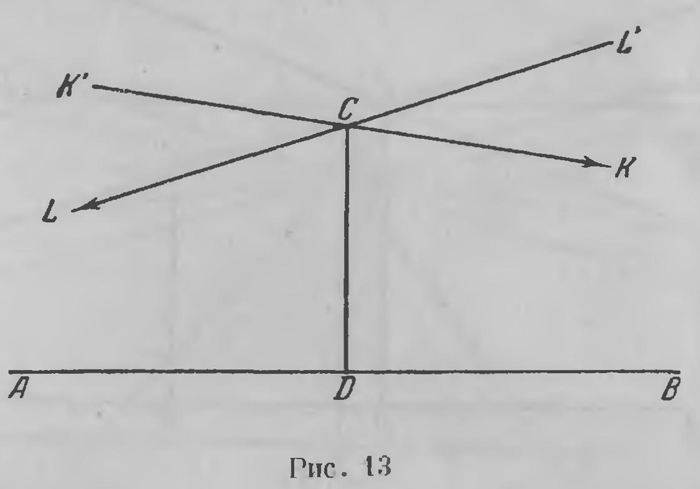

Каждый из равных острых углов DCK и DCL (рис. 13), которые параллели образуют с двух сторон с перпендикуляром CD, Лобачевский называет углом параллельности в точке С относительно прямой АВ. Евклидова геометрия выделяется тем, что в ней угол параллельности всегда есть прямой угол. Если, следовательно, допущено существование геометрии Лобачевского, т. е. геометрии, в которой имеют место исходные его постулаты, то геометрия Евклида составит частный ее случай, соответствующий тому, что угол параллельности имеет постоянное значение и всегда равен прямому углу. Становясь на почву воображаемой, неевклидовой геометрии, Лобачевский с безукоризненной строгостью доказывает, что две параллельные между собой прямые неограниченно (асимптотически) приближаются одна к другой в сторону параллелизма (рис. 14), как бы сходятся где-то в бесконечно удаленной точке; в противоположную же сторону они неограниченно удаляются друг от друга. Две же расходящиеся прямые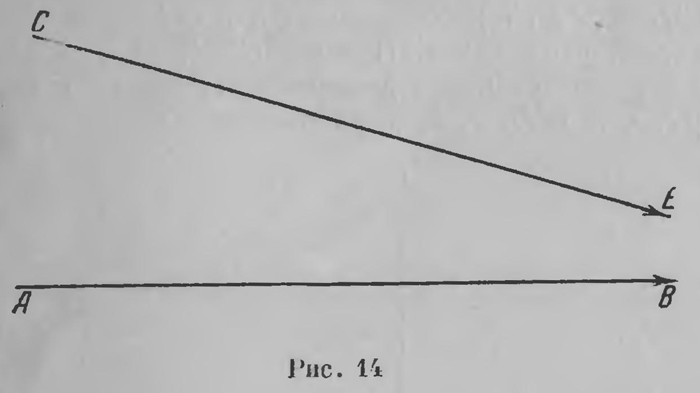

всегда имеют общий перпендикуляр, который представляет собой кратчайшее расстояние между ними, от которого они расходятся, неограниченно удаляясь одна от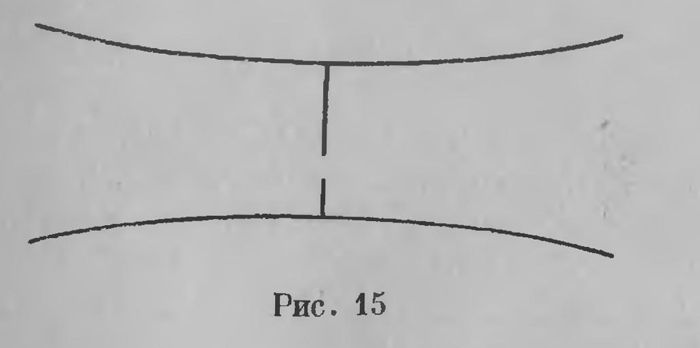

другой в обе стороны (риг. 15). Этот результат, обнаруживавшийся на первых шагах изучения неевклидовой геометрии, долго служил для мпогих непреодолимым препятствием к усвоению и признанию неевклидовой геометрии. Но справедливы слова Гаусса: «Мы не можем смешивать того, что нам кажется неестественным, с абсолютно невозможным».

Теперь возвратимся к углу параллельности. В неевклидовой геометрии это всегда острый угол и притом угол переменный. Пусть, как прежде (рис. 16), CD⊥АВ, СК || АВ, KCD есть угол параллельности в точке С относительно прямой АВ. Возьмем точку С' на том же перпендикуляре CD выше точки С. Если проведем прямую C'L под тем же углом к перпендикуляру, что и СК (∠DC’L = ∠РСК), то прямые СК и C’L, как евклидовы параллели, расходятся. Прямая С'К’, параллельная СК и АВ в ту же сторону, должна быть ближе к перпендикуляру, чем CL, т. е. угол параллельности в точке С'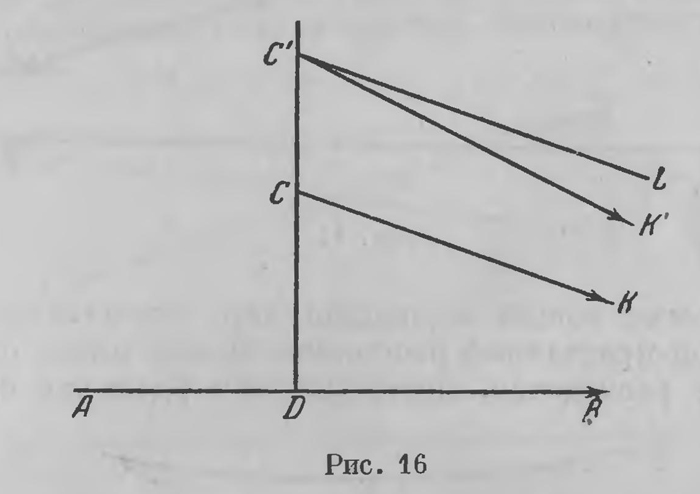

меньше, чем в точке С (∠К'СD∠KCD). Угол параллельности в точке С относительно прямой АВ, таким образом, зависит от расстояния точки С от АВ и представляет собой функцию этого расстояния. Если обозначим это расстояние CD через х, то угол параллельности в точке С есть функция от х. Лобачевский обозначил ее через П (х). Предыдущие соображения обнаруживают также, что эта функция убывает с возрастанием х. Так как П (х) есть острый угол, то отсюда следует, что с убыванием х угол DC К приближается к прямому углу. Лобачевский показывает, что он приближается к прямому углу неограниченно, это значит, сколь бы ни был мал угол а, значение П (х) отличается от прямого угла меньше чем на а, когда х становится достаточно малым. Лобачевский в следующей работе делает отсюда далеко идущие конкретные выводы; мы к ним придем ниже (гл. XVII). Для выяснения развития, которое Лобачевский дал своей геометрии, необходимо остановиться еще на двух моментах.

Представим себе окружность и совокупность, как говорят обыкновенно, «пучок», прямых, проходящих через ее центр. Окружность пересекает все прямые этого пучка ортогонально, т. е. под прямым углом. Можно это представить так: если наблюдатель движется по окружности,
то направление его движения все время обращено перпендикулярно к радиусу, его путь пересекает ортогонально все радиусы; геометр дает этому такое выражение: окружность есть ортогональная траектория пучка прямых, проходящих через одну точку—через центр этой окружности, через центр пучка. Это происходит одинаково в евклидовой и в неевклидовой плоскости.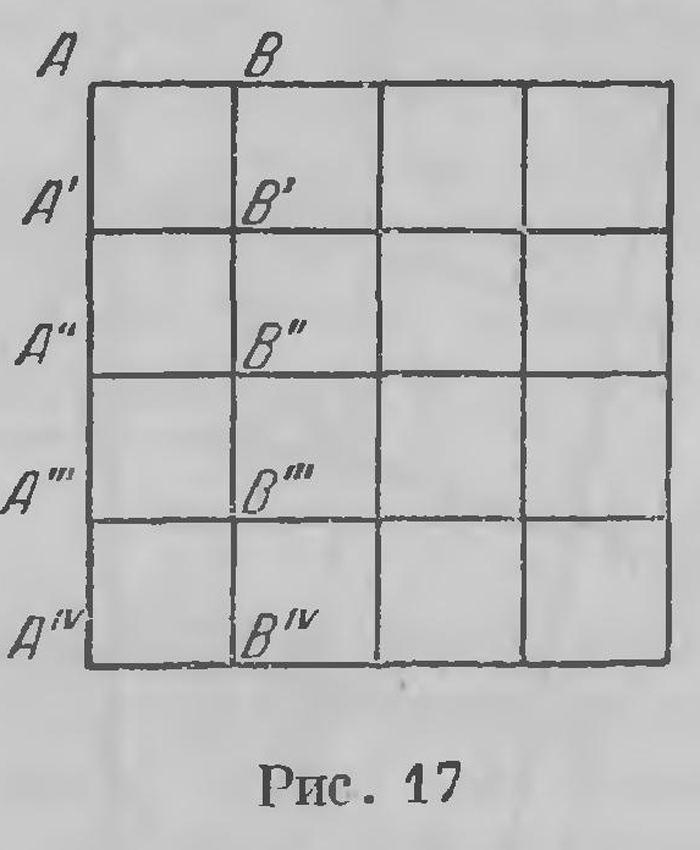

Представим себе теперь, что центр пучка удаляется по одной из прямых пучка; тогда прямые, составляющие пучок, как бы приближаются к параллелизму. Если заменим пучок прямых, пересекающихся в общей точке, пучком параллелей, то в евклидовой плоскости их ортогональными траекториями будут служить прямые (рис. 17); расстояние между двумя параллелями, отсчитываемое по траектории, на всем протяжении одно и то же. В плоскости Лобачевского дело обстоит иначе: так как параллели сближаются, то ортогональными траекториями служат своеобразные кривые (рис. 18), которые Лобачевский называет предельными окружностями или просто предельными линиями. Если представлять себе, что параллели пучка сходятся в бесконечно удаленной точке, то можно сказать, предельная линия — это окружность, центр которой лежит в бесконечности. Расстояние между параллелями в различных точках будем измерять дугами проходящих между ними предельных линий — соответственными предельными дугами (см., например, АВ, А'В', А"В",... на рис. 18). Различие между геометрией Евклида и геометрией Лобачевского заключается в том, что в первой это расстояние между двумя параллелями постоянно, а в геометрии Лобачевского оно убывает в сторону параллелизма. Легко показать (мы не можем здесь на этом останавливаться), что отношение этих расстояний, т. е. предельных дуг АВ и А'В’, здесь зависит только от того, насколько эти дуги одна от другой удалены, т. е. от длины отрезка А А' = ВВ'.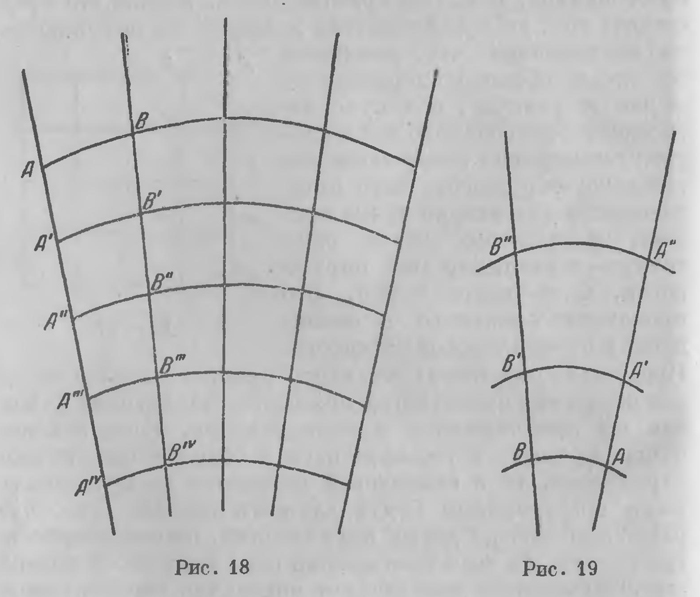

Имея это в виду, возьмем между параллелями две предельные други АВ, А'В', отстоящие одна от другой на расстояние А А' — ВВ', равное единице длины (скажем 1 см); отношение АВ : А'В’ представит собой некоторое определенное число, выражающееся неправильной дробью; обозначим ее через q.

Если будем отодвигаться в сторону параллелизма на расстояние

АА' = А'А''=А''А'''= ... = 1,

то

AB:A’B’ = q; А'В' :A"B" = q; А"В":An'B"' — q;

AB:A"B" = q² АВ : A"' B"' = q³ ... (7)

Если расстояние между предельными дугами l и l₀ составит n единиц длины, то отношение их длин l:l₀ = qⁿ, т. е. l=l₀qⁿ. Обычными приемами нетрудно обнаружить, что это соотношение остается в силе, когда расстояние между дугами выражается не целым числом, а любым дробным, даже иррациональным числом х всегда

l=l₀q^x. (8)

Точнее, существо дела заключается в следующем. Пусть АВ, А'В', А"В" произвольные три предельные дуги (рис. 19), содержащиеся между теми же осями; х и у — расстояния между ними, отсчитываемые по оси (х = А А', у = А' А"). Обозначим через φ (х) отношение предельных дуг, отстоящих одна от другой по оси на расстояние х. Тогда

А'В'=АВφ(х); А"В"=АВ’φ(у); А"В"=АВφ(х+у)

и поэтому

φ(х)φ(у)=φ(х+у). (9)

Функция φ(х) должна, таким образом, удовлетворять функциональному уравнению (9). Коши показал, что единственная непрерывная функция, ему удовлетворяющая, есть q^x, где q — постоянное положительное число.

Соотношение (8) лежит в основе всей метрики, т. е. измерения всех величин в геометрии Лобачевского. Какое же значение имеет эта неожиданно появившаяся постоянная q? Прежде всего ясно, что неевклидовой геометрии, где всегда АВ=А’В'= А"В", q=1; в геометрии же Лобачевского q>1. Необходимо было выяснить, какое значение эта постоянная должна иметь; мы к этому скоро вернемся (гл.XVII), теперь же обращаемся к дальнейшим рассуждениям, которые в рассматриваемых мемуарах развивают эти результаты. Это связано с углубленным рассмотрением двумерной геометрии в пространстве Лобачевского.

Планиметрия есть геометрия плоскости. Но ведь не только плоскость имеет свою двумерную геометрию; строго говоря, такую геометрию имеет всякая поверхность. Однако в более узком смысле можно сказать, что в обыкновенном евклидовом пространстве специфическую геометрию имеют поверхности двух типов: плоскость и сфера. Это нужно понимать следующим образом. К числу основных приемов, которыми мы пользуемся при построении геометрии плоскости, относится наложение одной фигуры на другую, т. е. передвижение фигур по плоскости. Плоскость допускает передвижение в пей фигур без деформации, причем любая точка фигуры может быть приведена в совмещение с любой точкой плоскости; зафиксировав же одну точку, можно в плоскости ее вокруг этой точки вращать. Те же движения возможны и на сфере. Поэтому на сфере также можно строить геометрию, пользуясь движением, наложением фигур. При таком построении прямые заменяются геодезическими линиями сферы, т. е. теми линиями, которые здесь, подобно прямым на плоскости, проходя между двумя точками, представляют кратчайшее расстояние между ними; хорошо известно, что эту роль на сфере играют окружности больших кругов.

Геометрия сферы была построена уже в древности. Основные положения, из которых исходит геометрия сферы — аксиоматика сферической геометрии, — существенно иные, чем на плоскости: здесь две геодезические линии — две окружности больших кругов — всегда пересекаются не в одной, а в двух точках; дуга геодезической линии может быть продолжена в обе стороны, но всегда возвращается в точку исхода, геодезическая линия имеет конечную длину; параллельных геодезических линий на сфере вовсе не существует. Сферическая геометрия в евклидовом пространстве, таким образом, существенно отличается от геометрии плоскости. Одно из ваяшейших ее отличий заключается в том, что сумма внутренних углов геодезического треугольника (т. е. треугольника, составленного из дуг больших кругов) всегда болъгие 2d. Итак, в евклидовом пространстве существует два типа поверхностей, которые допускают внутреннюю геометрию, основанную на движении без деформации: это геометрия плоскости и геометрия сферы. Другие поверхности полностью такой геометрии, без существенной модификации ее понимания, не допускают. Например, на трехосном эллипсоиде нельзя даже говорить о равенстве треугольников, ибо передвинуть треугольник с одного места на другое невозможно.

Так обстоит дело в евклидовом пространстве. Как это модифицируется в пространстве Лобачевского, т. е. в воображаемом пространстве, в котором царит геометрия Лобачевского? Плоскость и сфера и здесь имеют, конечно, каждая свою внутреннюю геометрию, в том смысле, как мы о таковой говорили выше. При этом геометрия сферы здесь совершенно та же, что и в пространстве Евклида. Это обусловливается тем, что здесь сохраняются все основные свойства сферы: две окружности больших кругов также пересекаются в двух точках, имеют одинаковую длину и т. д. Геометрия сферы в пространстве Лобачевского та же, что и в евклидовом пространстве. Напротив, плоскость несет здесь существенно другую геометрию — двумерную геометрию Лобачевского, основные черты которой выше уже достаточно отмечены.

Но зато в пространстве Лобачевского существуют еще другие поверхности, которые допускают внутреннюю геометрию, развертывающуюся теми же основными средствами, прежде всего свободным движением. Если предельную линию вращать вокруг какой-либо из ее осей, то получается своеобразная поверхность, которую Лобачевский называет предельной сферой или просто предельной поверхностью. Не точно, но образно, ее можно представить себе как сферу с бесконечно удаленным центром. Геодезическими линиями на этой поверхности служат предельные линии; такая поверхность может двигаться, скользить по себе самой так же, как плоскость и сфера: на ней можно строить внутреннюю геометрию теми средствами, о которых мы говорили выше. Что это за геометрия? Лобачевский обнаружил, что это обыкновенная евклидова геометрия. В пространстве Лобачевского предельная поверхность несет на себе двумерную евклидову геометрию. Когда мы отказываемся от евклидовой геометрии на плоскости, она не прекращает своего существования, она переходит на другую поверхность — на предельную поверхность.

Это восстановление евклидовой планиметрии в неевклидовом пространстве имеет чрезвычайно большое значение.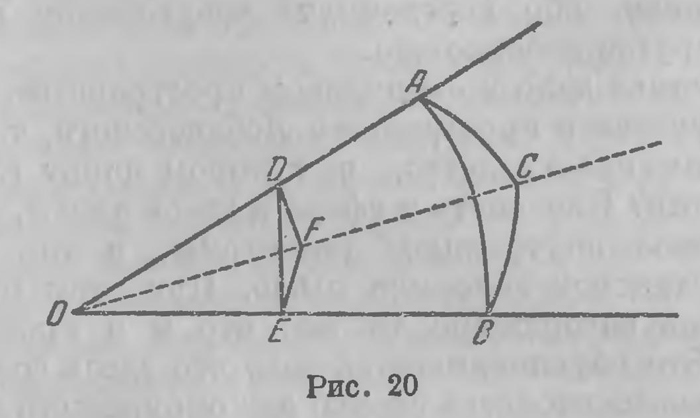

Вместе с нею сохраняются все средства евклидовой планиметрии и прежде всего ее тригонометрия. Благодаря этому получается возможность установить тригонометрию в пространстве Лобачевского, т. е. соотношения, которые в этом пространстве связывают стороны и углы прямолинейного треугольника. Чтобы уяснить себе, каким образом это осуществляется, припомним, как выводятся в евклидовом пространстве уравнения сферической тригонометрии; ограничимся простейшим случаем прямоугольного сферического треугольника.

Пусть ABC (рис. 20) — сферический треугольник с прямым углом при вершине С, О — центр сферы. Это значит, плоскости АОС и ВОС взаимно перпендикулярны; двугранный же угол при ребре OB (АОВС) измеряет угол В сферического треугольника. Из произвольной точки D на стороне ОА опускаем перпендикуляр DF на прямую ОС; он будет также перпендикуляром к плоскости ВОС. Наконец, из точки F опускаем перпендикуляр FE на прямую ОВ; угол DEF, как линейный угол двугранного угла при ребре ОБ, измеряет угол В сферического треугольника. Из прямоугольного треугольника DFE имеем

DF=DE sin DEF — DE sin В.

Но так как углы DOF и DOE измеряются соответственно сторонами Ь и с сферического треугольника, то

DF=OD sin b, DE=OD sin с;

подставляя эти выражения в предыдущее уравнение, получаем соотношение

sin b = sin с sin B; (10а)

и таким же образом

sin а = sin с sin А. (10b)

Совершенно аналогичными соображениями устанавливается третье уравнение

cos с=cos a cos Ь, (10с)

связывающее катеты и гипотенузу сферического треугольника.

На треугольник DFE мы можем смотреть как на центральную проекцию сферического треугольника АБС из центра О на плоскость DEF, перпендикулярную к ребру ОВ; соотношения, имеющие место в этой проекции, приводят к уравнениям (10а), (10b), (10с). Можно, конечно, и наоборот, смотреть на сферический треугольник АБС как на проекцию на сферу из ее центра плоского треугольника DEF.

Таким образом в евклидовом пространстве, исходя от плоскости, надлежащей проекцией на сферу получаем сферическую тригонометрию. В геометрии Лобачевского естественно исходить от предельной поверхности, несущей на себе наиболее простую, евклидову геометрию. Проектируя надлежащим образом ее предельные треугольники на плоскость, Лобачевский пришел к тригонометрии прямолинейного треугольника в своей воображаемой геометрии, т. е. установил уравнения, связывающие стороны и углы прямолинейного треугольника в воображаемой геометрии.

Как выглядят эти уравнения? Пусть а и Ь — катеты, с — гипотенуза, А и В — острые углы прямоугольного треугольника ЛВС. Каждому из отрезков а, Ь, с соответствует значение угла параллельности: П(а), П(b), П(с). Выполнив вычисления в том порядке, как это указано Быше, Лобачевский приходит к следующим тригонометрическим уравнениям прямоугольного треугольника
ABC:
ctg П(а)=ctg П(с)sin А, (11а)

ctg П(b)—ctg П(с)sin В, (11b)

sin П(a)sin П(b)— sin П(с). (11с)

Здесь тригонометрические функции угла имеют те же значения, какие они для того же угла (в градусном выражении) имеют в обыкновенной геометрии Всматриваясь в эти уравнения, видим, что первые два отличаются от соответствующих уравнений обыкновенной тригонометрии тем, что, вместо длин а, b, с соответствующих сторон треугольника, здесь фигурируют ctg П(а), ctg П(b), ctg П(с). Еще более своеобразный вид имеет соотношение (11с), выражающее связь между катетами и гипотенузой прямоугольного треугольника, заменяющее таким образом пифагорову теорему евклидовой геометрии. Мы, впрочем, увидим, что некоторое родство между этими уравнениями и соответствующими уравнениями обыкновенной тригонометрии не только существует, но даже не так глубоко сокрыто.

Из уравнений (11а) — (11с) уже можно чисто алгебраически получить выводные уравнения, которые часто бывают очень полезны. Так, уравнения

cos П(a) = ctgП(b)tg A, cos n(6) = ctg П(a) tgВ (11d)

определяют катет треугольника по другому катету и острому углу, противолежащему первому катету; а уравнения

cos П(a)=cos П(с) cos В, cos П(Ь) = cos П(с) cos А (11с)

определяют катет по гипотенузе и прилежащему к этому катету острому углу¹. Уравнения (11а) и (11b) обыкновенно называют теоремой синусов, уравнения (11с)—теоремой косинусов, уравнения (11d) — теоремой тангенсов.

Хотя уравнений (11а) — (11с) как будто достаточно для решения прямоугольного треугольника, но фактически мы воспользоваться ими еще не в состоянии: это было бы возможно, если бы мы умели по данным а, Ь, с определять соответствующие значения углов П(а), П(Ь), П(с) и обратно. Мы упираемся, таким образом, в задачу о разыскании аналитического выражения функции П(х) через ее аргумент х, к отысканию функции П(х), как говорит Лобачевский. Он хорошо понимал, что уравнения (11) получат конкретные значения только после того, как эта функция будет разыскана; на этом теперь было сосредоточено главное внимание. И ему это удалось выполнить. Опираясь уже на соотношения (11), Лобачевский показал, что функция ctg ½П(х) удовлетворяет тому же функциональному уравнению (9), которым она также определяется; именно при всяком значении х

ctg ½П(х)=q^х, (12)

где постоянная q имеет то же значение, что и в уравнении (8)². Соотношение (12) обыкновенно называют основным уравнением геометрии Лобачевского. С его помощью все вопросы метрической геометрии разрешаются; когда оно было найдено, элементы новой «воображаемой» геометрии были установлены.

Уравнениями (11) и (12), как указывает Лобачевский, заканчивалось рассуждение «Exposition succinеte». Из них очень просто, чисто алгебраически выводятся также уравнения косоугольного треугольника, которыми заканчиваются и «Геометрические исследования».

Этот небольшой очерк может, конечно, дать только самое общее представление об элементах геометрии Лобачевского. В настоящее время нетрудно уяснить их себе более обстоятельно. Читателю, который захочет приобрести эти сведения, не обращаясь к большим сочинениям, можно порекомендовать прекрасную статью проф. П. А. Широкова, в сборнике, изданном Академией Наук, указанную на стр. 9; она требует только четкого знания элементарной геометрии и некоторой общей математической культуры. Читатель, ознакомившийся с изложенным выше очерком и прочитавший статью Широкова, может прочесть уже и самые «Геометрические исследования» Лобачевского, комментированное издание которых указано па стр. 170.

Заканчивая обзор этого небольшого, но весьма замечательного сочинения, интересно остановиться на следующем вопросе. Как уже сказано выше, оно появилось на немецком языке; титульный лист его воспроизведен на стр. 187. Из него видно, что оно выпущено небольшим научным издательством Финке (Fincke) в Берлине. Возникает интересный вопрос, каким образом эта брошюра попала в такое мало известное издательство и что побудило это издательство выпустить в свет столь своеобразное сочинение казанского профессора, имя которого тогда в Германии вряд ли было известно? Об этом было немало споров и догадок. Ф. Энгель в сочинении, указанном на стр. 7, высказывает предположение, что его доставил в Берлин проф. Э. А. Кнорр, состоявший в первой половине сороковых годов профессором физики и физической географии в Казанском университете. По свидетельству сына Кнорра, его отец был в хороших отношениях с Лобачевским, в 1840 г. был в Германии и мог передать рукопись для напечатания издательству финке. Однако аргументация Энгеля очень слаба; она основана на предположении, что Гаусс смешал астронома Николаевской обсерватории К. Кнорре (К. Кnоrrе), о котором он собственно говорил, с казанским физиком Э. А. Кнорром.

Нам кажется более вероятной другая гипотеза. С 1809 по 1814 г. в Казанском университете состоял профессором права И. А. Финке. По наведенным справкам фамилия финке была мало распространена в Германии. Не лишено некоторого вероятия, что профессор Финке находился в родстве с берлинским издателем К. Финке. Правда, проф. Финке умер значительно раньше. Но его семья оставалась в Казани, была связана с Лобачевским, и через нее могло быть организовано издание «Geometrische Untersuchungen».

Таким образом, в феврале 1826 г. новая геометрия в своих основах была Лобачевским построена. Впрочем, оставалось еще ответить на вопрос, какое же значение имеет постоянная q. И, что не менее важно, оставалось еще выяснить, привели ли все эти рассуждения к безупречной, новой геометрии; стоял еще ряд вопросов, которые, конечно, возникают у читателя, которые возникли и у Лобачевского. Свет на эти вопросы проливает дальнейшее развитие тех же идей.

¹Приведем для ясности такой вывод. Перемножая уравнения (11а) и (11c), получим:
cos П(a) sin П(b) — cos П(с) sin А. (11с')
Исключая угол П(с) из уравнений (11с) и (11с'), легко получим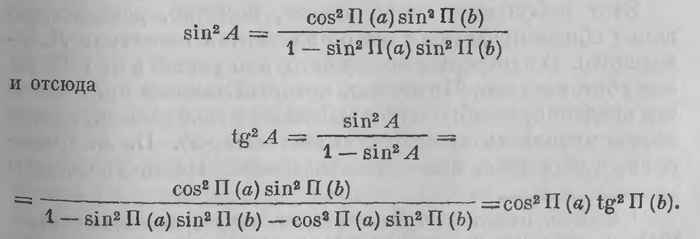

По извлечении корня из обеих частей получим первое уравнение (11d).
²Следует отметить, что совершенно безукоризненное доказательство того, что постоянная q здесь имеет то же значение, что и в уравнении (8), было дано Лобачевским значительно позже 8 сочинении «Пангеометрпя» (см. гл. XXVII) .

<<Назад Вперёд>>

Просмотров: 4949

загрузка...

Другие книги по данной тематике