XIII. Учение о параллельных линиях от Евклида до Лежандра
|
до Лежандра
«В геометрии,—пишет Лобачевский в введении к Геометрическим исследованиям по теории параллельных линий,— я нашел некоторые несовершенства, которые я считаю причиной того, что эта наука, поскольку она не переходит в анализ, до настоящего времени не вышла ни на один шаг за пределы того состояния, в каком она к нам перешла от Евклида. К этим несовершенствам я отношу неясность в первых понятиях о геометрических величинах, способы, которыми мы себе представляем измерение этих величин, и, наконец, важный пробел в теории параллельных линий, к восполнению которого все усилия математиков до настоящего времени были тщетными». Нужно четко уяснить, в чем этот пробел заключается* Учение о параллельных линиях Евклид строит, так сказать, па двойном базисе. Первым фундаментом этого учения служит 16-е предложение книги I (116), т. е. первая теорема о внешнем угле треугольника: внешний угол треугольника больше каждого из внутренних с ним не смежных углов. При пересечении двух прямых, расположенных в одной плоскости, третьей (рис. 2) образуется 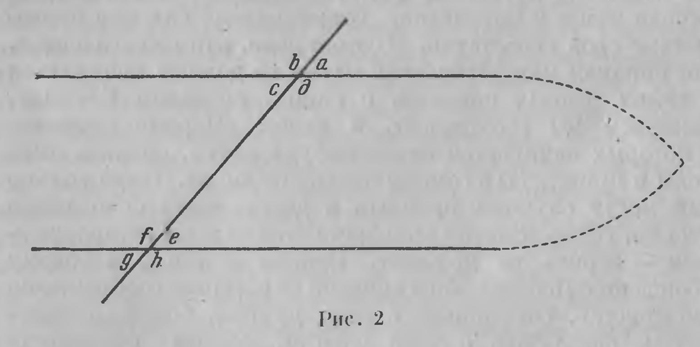
8 углов, которые в парных комбинациях получают различные названия. Если из внутренних накрест лежащих углов какие-либо два равны между собой, т. е. если с = е или d = f, (1) то линии параллельны; в самом деле, если бы эти прямые пересекались, то образовался бы треугольник, в котором один из внешних углов был бы равен внутреннему, с ним не смежному, что противоречит предложению I16. Отсюда следует, что линии параллельны также, если равны два внешних накрест лежащих угла, т. е. если имеет место одно из равенств а = g или b = h (2) или если равны два соответственных угла а = е, b = f, c = g, d = h, (3) или если какие-либо два внутренних или два внешних односторонних угла составляют вместе 2d, т. е. если с+f-f=2d, или d+e=2d, или а+h=2d, или b+g=2d. (4) Дело в том, что каждое из 12 равенств (1) — (4) влечет за собой все остальные 11. Мы приходим таким образом к теореме, которая вытекает, главным образом, из предложения, связанного с равенством (1): Теорема. Если при пересечении двух прямых, лежащих в одной плоскости, третьей имеет место одно из равенств (1) — (4), то эти прямые параллельны. Эта теорема разбита у Евклида на два предложения I27 и I28, которые в совокупности составляют так называемую прямую теорию параллельных линий; она устанавливает 12 равенств, каждое из которых достаточно для того, чтобы две прямые, расположенные в одной плоскости, были параллельны; она доказывается на основе предыдущих предложений, главным образом на основе теоремы о внешнем угле треугольника I16. В таком виде эти предложения излагаются во всех элементарных учебниках геометрии. Возникает обратный вопрос: если известно, что две прямые параллельны, то можно ли утверждать, что имеют место равенства (1)—(4)? Можно ли утверждать, что каждое из этих равенств выражает не только достаточное, но и необходимое условие параллельности двух прямых? Справедлива ли теорема, обратная предыдущей? Мы привыкли к тому, что за доказательством каждой теоремы следует доказательство обратной теоремы, если только она справедлива. Так как и в этом случае справедливость обратной теоремы не вызывала сомнений, то было естественно искать ее доказательство. История науки знает ряд вопросов, проблем, разрешение которых долгое время представляло камень преткновения для математической мысли. Простейшие из этих проблем возникли еще в глубокой древности. Древнейшей из них была, по преданию, так называемая «Делийская задача», требовавшая по указанию оракула удвоения куба, стоявшего на жертвеннике Аполлона; задачу надо понимать так, чтобы циркулем и линейкой построить сторону куба, имеющего по сравнению с данным кубом двойной объем. Столь же неприступными были задачи о трисекции угла и квадратуре крута, т. е. задача о построении теми же средствами угла, составляющего третью часть данного угла,— квадрата, равновеликого данному кругу. К числу таких недоступных задач принадлежало также требование доказать обратную теорему в учении о параллельных линиях, т. е. выполнить это доказательство теми же средствами, которыми доказаны предыдущие 27 предложений в «Началах» Евклида. Не подлежит сомнению, что такое доказательство усердно искали уже до Евклида, и это не удавалось. Подобно Александру Македонскому, Евклид решил разрубить гордиев узел: он принял обратное предложение за постулат, подлежащий в качестве такового приобщению к первым четырем постулатам. Согласно этой установке, каждый приступающий к изучению геометрии должен был признать, что при пересечении двух параллельных линий третьей необходимо должны иметь место равенства (1) — (4); т. е. собственно принять нужно было только, что при пересечении двух параллельных линий третьей имеет место хотя бы только одно из равенств (1) — (4), так как каждое из них влечет за собою остальные. Евклид принимает, что при пересечении двух параллельных линий третьей имеет место какое-либо одно из равенств (4). Таким образом, Евклид принимает в качестве постулата, что при пересечении двух параллельных прямых третьей сумма внутренних односторонних углов равна 2d, или — что, очевидно, то же — если при пересечении двух прямых, лежащих в одной плоскости, третьей сумма внутренних односторонних углов не равна двум прямым, то эти прямые не параллельны, они неизбежно пересекаются. Таков дополнительный постулат, который Евклид вводит, которым он пользуется, начиная с 29-го предложения I книги. Чтобы в этом узловом пункте быть вполне точным, нужно остановиться еще на одной детали. Из теоремы о внешнем угле непосредственно вытекает, что сумма двух углов треугольника никогда не может превысить 2d. Это и составляет содержание следующего предложения I17. В самом деле, если А и В внутренние углы треугольника ABC (рис. 3) при основании АВ, А' и В'— соответствующие смежные углы, то сумма четырех углов А + А' + В+ B’ = 4d. (5) Но так как А 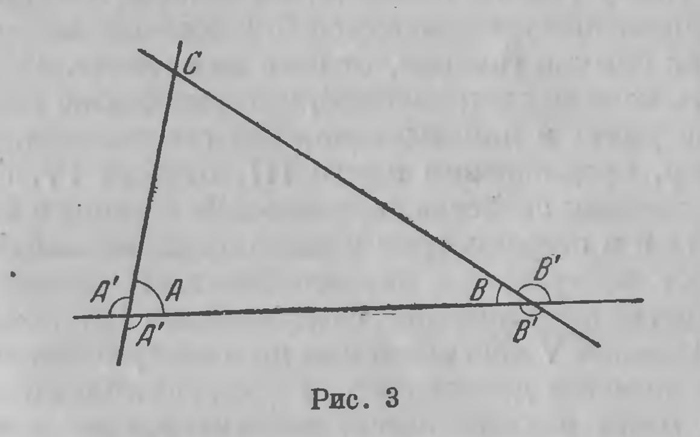
имеет место с той стороны секущей АВ, с которой сумма внутренних односторонних углов меньше 2d. Теперь мы можем привести постулат о параллельных точно в топ форме, в которой мы его находим в «Началах» Евклида. Это и есть V постулат, которого мы не привели выше (стр. 159) при перечислении первых четырех. Постулат V. Если при пересечении двух прямых [лежащих в одной плоскости] третьей сумма внутренних односторонних углов меньше 2d, то эти прямые при достаточном продолжении пересекаются и притом с той стороны, с которой эта сумма меньше 2d. Конечно, дополнения, относящегося к тому, с какой стороны происходит пересечение, Евклид мог бы уже не приводить; это, как мы видели, уже вытекает из предыдущего. Но мы хотели формулировать этот постулат, который так часто называют просто постулатом Евклида, так, как это сделано им. Мы уже упоминали выше, что в различных изданиях «Начал» расхождения чаще всего относятся к постулатам и аксиомам. Некоторые издатели вовсе не отличают постулатов от аксиом, и тогда постулат о параллельных фигурирует у них в качестве XI аксиомы, иногда даже в качестве XII и XIII аксиомы. Так возник знаменитый постулат, послуживший отправной точкой разветвления геометрии. И таковой он является уже у самого Евклида: мы видели, что 28 первых его предложений доказываются без помощи этого постулата, как обычно говорят, от него не зависят. Н дальнейшем есть немало предложений, которые также не зависят от V постулата и доказываются без его помощи. Таковы, например, предложения книги III, отчасти IV, содержащие простейшие свойства окружностей, их хорд и касательных; есть и в стереометрии немало предложений, не зависящих от постулата о параллельных. Но подавляющее большинство предложений, следующих за I28, доказываются при помощи V постулата или других предложений, уже при его помощи доказанных. Геометрия, таким образом, с этого места разветвляется, распадается на две части: первую часть образуют те предложения, которые от постулата не зависят: их совокупность в настоящее время называют абсолютной геометрией; вторую составляют предложения, которые, как уже было ясно Евклиду, без этого постулата доказаны быть не могут; эти последние образуют так называемую собственно евклидову геометрию. Таким образом, постулат о параллельных линиях носит совершенно своеобразный характер: по своему содержанию он сложнее других; для его понимания нужен уже ряд предварительных сведений; он появляется поздно, после 28-го предложения книги I, тогда как остальные постулаты оказываются необходимыми при доказательстве первых теорем; наконец, этот постулат как бы расщепляет геометрию на две части — на абсолютную и собственно евклидову геометрию. Теперь становится ясным то странное расположение материала, которое мы находим в «Геометрии» Лобачевского, т. е. в учебнике, который он представил в 1823 г. В первых пяти главках Лобачевский тщательно отобрал тот материал, который в планиметрии и стереометрии не зависит от постулата о параллельных. К этому мы очень скоро возвратимся. Вследствие своеобразного характера V постулата на нем было особенно сосредоточено внимание комментаторов. Его часто заменяли другим эквивалентным ему постулатом, который казался более простым. Так, английскому математику Плейферу, с которым мы уже встречались выше (стр. 122), приписывают следующую формулировку постулата. Постулат Плейфера. Через точку С, лежащую вне прямой АВ, в плоскости АБС проходит только одна прямая, не встречающая АВ. Нужно сказать, что эта формулировка встречалась у различных авторов до Плейфера, но мы сохраним установившуюся номенклатуру. Очень распространена также еще следующая формулировка, связываемая с именем Лежандра. 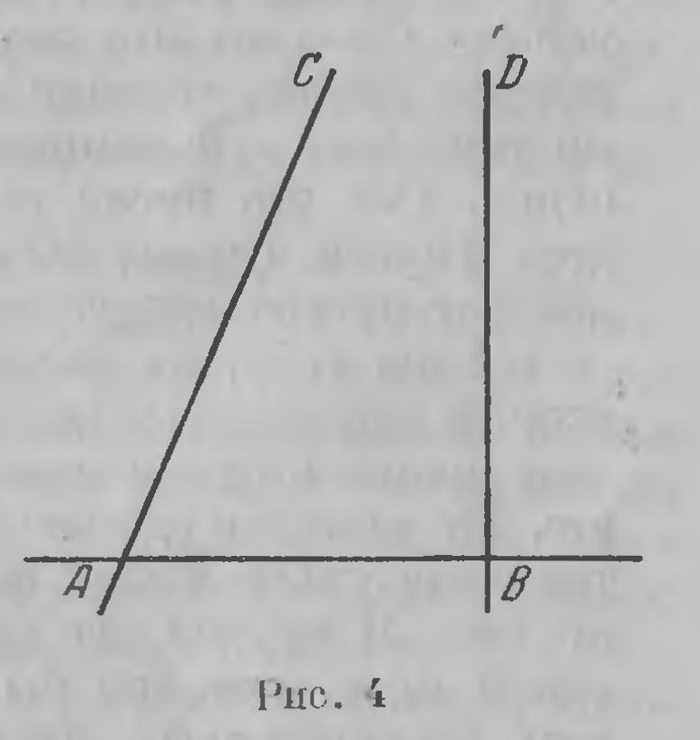
Постулат Лежандра. Перпендикуляр и наклонная к общей секущей, расположенные в одной плоскости, необходимо встречаются [конечно, с той стороны секущей, с которой наклонная образует с секущей острый угол (рис. 4)]. В этой форме постулат введен Лежандром в его «Началах»; но и она встречается в различных сочинениях гораздо раньше, например, у Валлиса в XVII в., строго говоря, даже раньше — у арабского геометра Насир-Эддина (1201—1274). В этих формулировках постулат можно встретить в различных элементарных учебниках геометрии, и мы не будем здесь останавливаться на доказательстве того, что они эквивалентны постулату Евклида. Но если наиболее осторожные комментаторы Евклида ограничивались тем, что заменяли постулат Евклида другим, ему эквивалентным, то другие шли дальше. Стремились логически вывести содержащееся в этом постулате утверждение из первых 28 предложений, строго говоря, следовательно, из остальных аксиом и постулатов Евклида: как обычно говорят, стремились доказать постулат о параллельных линиях. Трудно себе представить, сколько усилий было на это затрачено. Люди ставили себе это задачей жизни, тратили на это многие годы, доходили до мистического агностицизма, а иногда даже до потери рассудка. Вот что писал венгерский профессор В. Болани, друг Гаусса, своему сыну Иоанну, узнав, что он ищет доказательство постулата о параллельных линиях: «Молю тебя, не делай только и ты попыток одолеть теорию параллельных линий: ты затратишь на это все свое время, а предложения этого вы не докажете все вместе. Не пытайся одолеть теорию параллельных линий ни тем способом, который ты сообщаешь мне, ни каким-либо другим. Я изучил все пути до конца: я не встретил ни одной идеи, которой бы я не разрабатывал. Я прошел весь беспросветный мрак этой ночи, и всякий светоч, всякую радость жизни я в ней похоронил. Ради бога, молю тебя, оставь эту материю, страшись её не меньше, нежели чувственных увлечений, потому что и она может лишить тебя всего твоего времени, здоровья, покоя, всего счастья твоей жизни. Этот беспросветный мрак может потопить тысячи ньютоновских башен. Он никогда не прояснится на земле, и никогда несчастный род человеческий не будет владеть чем-либо совершенным даже в геометрии. Эта большая и вечная рана в моей душе...» Не в столь экспансивном, но, по существу, в том же стиле писал в 1817 г. Гаусс: «Я все больше прихожу к убеждению, что необходимость нашей геометрии не может быть доказана, по крайней мере, человеческим умом для человеческого ума». Правда, среди лиц, которые занимались доказательством V постулата, часто бывали люди, не только лишенные математического образования, но даже не владевшие элементарными сведениями из геометрии. Но в то же время почти не было выдающегося математика, который не уделил бы внимания и сил этой проблеме: Ампер, Лейбниц, Декарт, Лагранж, Лежандр, Фурье, Гаусс, Якоби — все пытались доказать постулат, старались пролить свет на это «темное пятно в теории параллельных линий». Многим казалось, что они достигли цели; этой иллюзии не избежал даже такой крупный геометр, как Лежандр. Но тщательный и объективный анализ неизменно обнаруживал несостоятельность рассуждения. Этой участи не избежали и доказательства, отличавшиеся несомненным остроумием. «Доказательства постулата Евклида, — говорит германский математик и философ середины XVIII в. Ламберт (J. Н. Lambert) (см. ниже, стр. 400), — могут быть доведены столь далеко, что остается, повидимому, только одна мелочь. Но при тщательном анализе оказывается, что в этой кажущейся мелочи и заключается вся суть вопроса; обыкновенно она содержит либо доказываемое предложение, либо равносильный ему постулат». Уже в XVIII в. молодой германский математик, Клюгель, ученик известного Кестнера (A. Kastner), занимавшего в то время кафедру Евклида в Геттингенском университете, представил диссертацию о параллельных линиях1; он приходит к заключению, что ни одно из доказательств постулата не выдерживает строгой критики. Почти через сто лет после этого сочинение, посвященное доказательствам постулата о параллельных линиях, выпустил русский математик В. Я. Буняковский2. Читатель, которого это заинтересует, найдет изложение наиболее интересных доказательств в книге Бонола3 и во вводной статье В. Ф. Кагана к «Геометрическим исследованиям» Лобачевского, помещенной в I томе полного собрания его сочинений4. Здесь мы все же приведем два доказательства, чтобы дать некоторое представление об этих рассуждениях. Почти все доказательства постулата, как сказано в приведенной выше цитате из Ламберта, грешат тем, что они явно или неявно допускают положение, эквивалентное доказываемому постулату. Это ясно видно на тех примерах, которые мы приведем. Начнем с доказательства Валлиса. Еще в XVII в. в Оксфордском университете была учреждена кафедра для спорадического чтения лекций по Евклиду. Одним из первых профессоров (professor Sevilianus), занимавших эту кафедру, был Дж. Валлис (J. Wallis, 1616—1703); его труды по алгебре и по анализу бесконечно малых хорошо известны; это был один из прямых предшественников Ньютона в деле создания анализа бесконечно малых. В 1663 г., выполняя лежащее на нем обязательство, он прочел лекцию, содержавшую доказательство постулата о параллельных. Несколько модифицируя рассуждения Валлиса5, изложим существо его доказательства постулата применительно к той его форме, которой, как уже указано, неправильно присваивается имя Лежандра. Нужно, следовательно, доказать, что перпендикуляр АВ.и наклонная CD к секущей АС непременно пересекаются со стороны острого угла ACD (рис. 5). С этой целью, следуя общему замыслу Валлиса, опустим из точки F луча CD на прямую С А перпендикуляр, который упадет в точку G со стороны острого угла. После этого построим треугольник С'А'Е', подобный треугольнику CGF при отношении соответственных сторон, равном СA:GC тогда сторона С'А' будет равна СА и ∠ А'С'Е' = ∠ ACD. Если приложим треугольник А'С'Е' к прямой АС с надлежащей стороны так, чтобы сторона его А'С' совпала с отрезком АС, то прямые А'Е' и С'Е' пойдут соответственно но АВ и CD, и точка Е' упадет в точку Е, в которой перпендикуляр А В пересечется с наклонной CF (рис. 5 и 6). 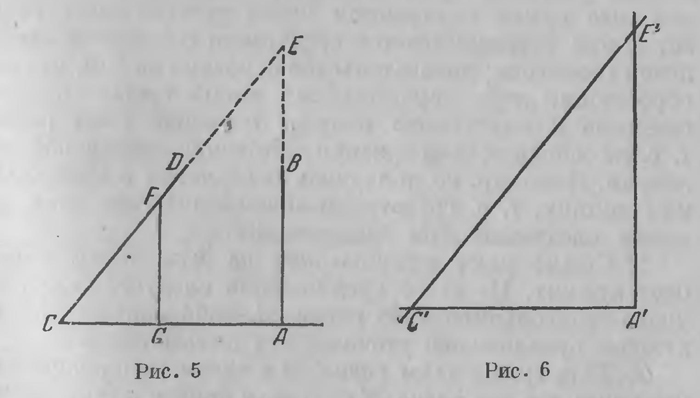
Рассуждение кажется безукоризненным; но оно предполагает, что каждому треугольнику отвечает подобный ему треугольник при любом отношении подобия. Валлис это постулирует, четко это оговаривая. Но такое допущение не только эквивалентно постулату Евклида, а даже избыточно: достаточно принять, что на плоскости существуют какие-либо два подобных треугольника, и из этого допущения вытечет постулат о параллельных, а с ним вся евклидова геометрия. Между тем задача, как уже указано заключается отнюдь не в том, чтобы заменить постулат о параллельных более простым (постулат Валлиса не является более простым), а в том, чтобы «доказать постулат», не пользуясь никаким добавочным допущением. Минуем полтораста лет и обратимся к рассуждениям Лежандра. К размышлениям о теории параллельных линий Лежандра привело составление учебника геометрии, о котором нам уже пришлось говорить выше (стр. 129), новых «Начал», которые впервые заменили книгу Евклида во многих школах. Точкой отправления Лежандра служит учение о сумме углов треугольника. Теорема о том, что сумма внутренних углов треугольника равна 2d, всегда устанавливается средствами собственно евклидовой геометрии: доказательство основано на том, что при пересечении двух параллельных линий третьей соответственные и внутренние накрест лежащие углы равны, т. е. на основном предложении собственно евклидовой геометрии. Лежандр, не пользуясь постулатом о параллельных линиях, т. е. средствами абсолютной геометрии, доказал следующие три предложения: 1. Сумма углов треугольника не может превышать двух прямых. Из этого предложения следует, что сумма углов треугольника либо равна 2d, либо меньше 2d. Следующее предложение уточняет эту дизъюнкцию. 2. Если сумма углов равна 2d в каком-либо одном треугольнике, то она равна 2d во всяком другом треугольнике. Таким образом, средствами абсолютной геометрии устанавливается, что сумма внутренних углов во всех треугольниках либо равна 2d, либо же меньше 2d. 3. Если сумма внутренних углов треугольника равна 2d, то имеет место постулат о параллельных, а следовательно, вся геометрия Евклида. Таким образом, постулат Евклида эквивалентен допущению, что сумма углов треугольника равна 2d. Доказательства этих теорем читатель найдет частично в «Началах» Лежандра (издания III—VIII), полностью — в указанных выше книге Бонола и статье В. Ф. Кагана. Из теорем Лежандра, таким образом, следует, что для доказательства постулата о параллельных достаточно установить средствами абсолютной геометрии, что сумма углов треугольника равна 2d. Предложенное им доказательство, в высшей степени остроумное, мы воспроизводим здесь полностью. Продолжим стороны АВ и АС треугольника ABC и приложим его к стороне ВС, повернув его при этом так, чтобы вершина В упала в точку С, а вершина С — в точку В. Треугольник займет положение DCB. При этом ∠DBC — ∠ АСВ, ∠DCB = ∠АВС. А так как ∠ КВС, как внешний угол треугольника ABC, больше ∠АСВ, той ∠CBD меньше ∠СВК; сторона BD передвинутого треугольника расположится, следовательно, внутри угла СВК. 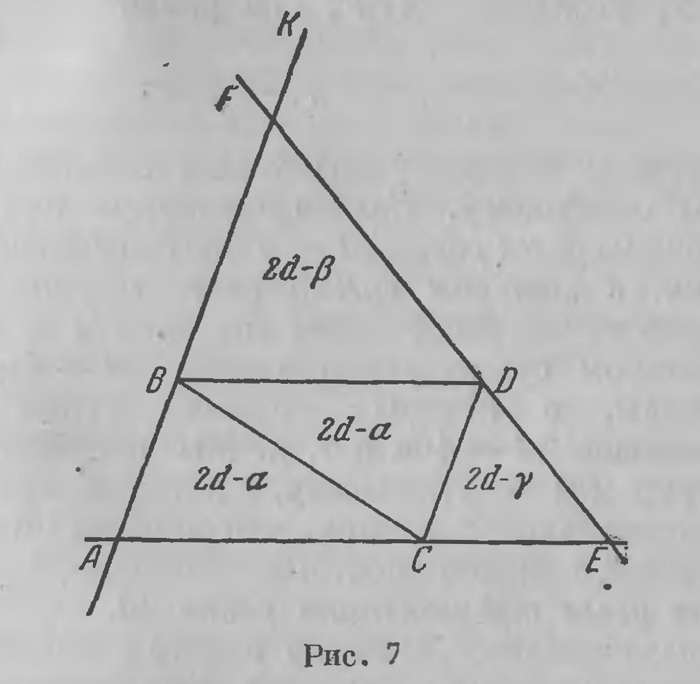
Таким же образом сторона CD расположится внутри угла ВСЕ; треугольник займет положение DCB, указанное на чертеже. Теперь через точку D проведем прямую EF так, чтобы она пересекала стороны угла ЕАК в точках Е и F. Мы придем к треугольнику AEF, который расположен внутри угла КАЕ и распадается на четыре треугольника, один из которых, BDC, не отличается от данного (ABC), два других же от них вообще отличны (рис. 7) Теперь Лежандр становится на путь доказательства от противного. Он допускает, что сумма углов треугольника ABC у меньше 2d, равна, скажем, 2d — а, где а имеет положительное значение; ту же сумму имеют внутренние углы треугольника BCD. В каждом из треугольников BFD и CED, согласно теореме 2, сумма углов также меньше 2d, составляя, скажем, 2d — β в треугольнике BDF и 2d — β в треугольнике CDE. Сумма внутренних углов во всех четырех треугольниках составляет поэтому 8d — 2α — β — γ. Если от этой суммы отбросить углы при точках В, С, D, т. е. 6d, по получим сумму внутренних углов треугольника AEF', она равна 2d — 2α — β —γ < 2d — 2α. (6) Результат, к которому мы таким образом пришли, сводится к следующему. Если существует, треугольник, в котором сумма углов, равно, 2d — α, то существует также треугольник, в котором сумма углов меньше 2d — 2α. Но, повторив то же построение, мы придем к треугольнику, в котором сумма углов меньше 2d — 4α, далее к треугольникам, в которых сумма углов меньше 2d — 8α, меньше 2d — 16α и т. д. Мы. неизбежно таким образом придем к треугольнику, в котором гумма углов имеет отрицательное значение, что лишено смысла. Сделанное предположение поэтому неправильно; сумма внутренних углов треугольника равна 2d. Это доказательство Лежандр излагал в своих «Началах» с третьего издания по восьмое. Ему, конечно, нельзя отказать в исключительном остроумии; но и оно все же страдает существенным недостатком, лишающим его доказательной силы. Именно, оно предполагает, что через точку D, лежащую внутри угла КАЕ, всегда можно провести прямую EF, встречающую обе стороны угла. А это есть допущение, эквивалентное постулату Евклида. И Лежандр, очевидно, сознавал, что в этом есть дефект. Это видно из следующего подстрочного примечания, помещенного в третьем издании. «Мы предположили, что А есть самый меньший из углов треугольника ABC и, следовательно, не превышает двух третей прямого угла; этим мы имеем в виду сделать более ощутительным, что прямая, проведенная через точку D, может одновременно встретить продолжения сторон АВ и АС». Совершенно ясно, что эта деталь ничего не меняет; это и было очень скоро обнаружено. Лежандр сохранил это доказательство, как уже сказано, с третьего по восьмое издание своих «Начал». В дальнейших изданиях «Начал», с девятого по одиннадцатое, он возвратился к схеме Евклида. В двенадцатом и тринадцатом изданиях появляется другая модификация того же доказательства. Лежандр этим не ограничился; он строил доказательство постулата и из совершенно другого принципа, известного под названием «начала однородности». Такое доказательство изложено им в приложении к третьему изданию «Начал». Об этом принципе мы будем говорить ниже; здесь же ограничимся замечанием, что это доказательство пе более убедительно, чем предыдущее. В последние годы своей жизни (1833) Лежандр опубликовал в «Мемуарах Парижской Академии наук» обширное исследование, носящее своеобразное название «Размышления о различных способах доказательства теории параллельных линий или теоремы о сумме углов треугольника»1. Это — именно размышления, к выводам из которых сам автор относится с большой осторожностью; он не делает уверенных утверждений, он собрал здесь, по выражению Лобачевского, «все, что по его мнению, казалось наиболее удовлетворительным»2. Мемуар Лежандра завершил эпоху в истории поисков доказательств постулата о параллельных линиях. В то время, когда он опубликовал свои заключительный мемуар, вопрос был полностью уже разрешен. Лобачевский за четыре года до того опубликовал уже свой основной мемуар «О началах геометрии», в котором весь вопрос получил исчерпывающее решение. Лобачевский тщательно изучил рассуждения Лежандра. Он указывает на них почти в каждом своем сочинении; но он не впал в ошибку, которую допустил Лежандр. Вот что он пишет в начале сочинения «Новые начала геометрии с полной теорией параллельных»3: «Не почитаю нужным распространяться здесь об этой ошибке, в которой сознался после сам Лежандр, говоря, что хотя в основание взятые начала не подлежат сомнению, но встречает однако затруднения, не будучи в состоянии победить их. В Записках Французской Академии 1833 года прибавил он еще предложение, что сумма углов должна быть π во всех треугольниках, если такова в одном только. То же мне надобно было доказывать ив моей теории, которую писал я в 1826 г. Даже нахожу, что Лежандр несколько раз попадал на ту дорогу, которую выбрал я так удачно; но вероятно предубеждение в пользу принятого всеми положения заставляло на каждом шагу спешить заключением или дополнять тем, чего бы нельзя было допускать еще в новом предположении». Лобачевский преодолел это предубеждение, и это привело его к его замечательному открытию. 1G. S. Кlugеl. Conatuum praecipiorum theoriam parallelarum demonstrandi recensio. Gottingen, 1763. 2В. Я. Буняковский. Параллельные линии. Напечатано в «Известиях Академии Наук» за 1850 г. и выпущено отдельным изданием. 3Р. Бонола. Неевклидова геометрия. Пер. с итальянского. СПб., 1910. 4В. Ф. Каган. Учение о параллельных линиях и открытие неевклидовой геометрии (Лобачевский. Полное собрание сочинений, т. I, М. — Л., 1944). Вышло также в отдельном издании: Лобачевский. Геометрические исследования по теории параллельных линий. Перевод, комментарии, вступительные статьи и примечания проф. В. Ф. Кагана. Изд. АН СССР, М. — Л., 1946. 5Рассуждения Валлиса очень пространны; мы вынуждены передать их в несколько сокращенном, даже измененном виде, не совпадающем с его текстом, по четко выражающем его основную мысль. 1А. М. Legendre. Reflexions sur les differentes manieres de demonstrer la theorie des paralleles ou le theoreme sur la somme ties trois angles du triangle. 2H. И. Лобачeвский. Воображаемая геометрия. Вступление. 3«Полное собрание сочипений по геометрии», т. I, стр. 250 |
загрузка...
