§ 54. Борьба вокруг статистического понимания второго закона термодинамики

В конце XIX в. на работы Больцмана по статистическому обоснованию второго закона термодинамики наконец обратили внимание. В 1894—1895 гг. на страницах английского журнала «Nature» развернулась полемика вокруг этих работ Больцмана. Ряд ученых выступили с возражениями против Н-теоремы, которые основывались на замечании Лошмидта по поводу абсолютной выполнимости второго закона термодинамики. Оно известно в литературе как возражение Лошмидта. Сущность его заключается в следующем. Представим себе два состояния газа z и z', в которых все частицы занимают соответственно одинаковые положения и имеют одинаковые по величине, но противоположные но направлению скорости. Соответствующие значения функции Я для этих состояний пусть будут H и Н', причем очевидно, что H = Н'. Если с течением времени для газа, проходящего состояние z, функция H непрерывно убывает или, если состояние стационарное, остается постоянным, так что H ≥ H₁ ≥ H₂ ≥ H₃, то для газа, проходящего состояние z', вследствие полной обратимости законов механики

H' = H'₁ = H'₂ = H'₃.

Таким образом, существует одинаковое число состояний газа, для которых функция Я с течением времени возрастает, и состояний, для которых она убывает. Значит, говоря словами одного из критиков Больцмана, Н-теорема «может быть применена к одному из движений при условии, если она неприменима к другому»¹, следовательно, эту теорему нельзя считать верной.

Больцман, возражая своим критикам², подчеркивал, что Н-теорема не утверждает, что величина Я при любых начальных состояниях системы обязательно убывает. Убывание функции Я является лишь наиболее вероятным и все выводы, вытекающие из этой теоремы, имеют вероятностный характер. Больцман представил графически характер изменений функции Я со временем. Если по оси абсцисс откладывать время, а по оси ординат³— соответствующее значение Н, то получим Н-кривую, которая имеет особый пикообразный характер, т. е. состоит сплошь из максимумов. При этом максимальные значения Н, заметно отличающиеся от наименьшего ее значения, встречаются очень редкой число таких максимумов очень быстро убывает по мере увеличения их значения (рис. 13). Если теперь наша система находится в неравновесном состоянии в какой-либо момент времени, то это может означать, что мы попали в точку, в которой кривая является или восходящей, или нисходящей, или же имеет максимум. Но так как число максимумов очень быстро убывает по мере возрастания их величин, то гораздо более вероятно, что мы попали в точку максимума, т. е. в точку, начиная с которой Н-кривая убывает, а не возрастает, как полагали критики Н-теоремы.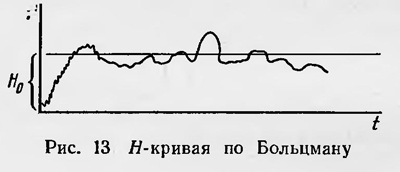

Против Н-теоремы было выдвинуто и другое возражение, основанное на теореме, которую доказал Пуанкаре. Пуанкаре показал, что всякая консервативная механическая система, которая заключена в ограниченном объеме, находящаяся в начальный момент времени t в состоянии А, через некоторый промежуток времени вновь приходит в первоначальное состояние, или, точнее, в состояние В такое, что значения величин, определяющих состояние, отличаются от их значения в состоянии А на наперед заданную, сколь угодно малую положительную величину. Согласно этой теореме, например, газ, заключенный в сосуд и находящийся в состоянии А, предоставленный самому себе, через некоторый промежуток времени должен возвратиться в первоначальное состояние с любой степенью точности. Но если начальное состояние газа являлось неравновесным и величина Н, соответствующая этому состоянию, не имела минимального значения, то хотя согласно Н-теореме она сначала уменьшается и газ переходит в состояние термодинамического равновесия, тем не менее через известный промежуток времени величина Н должна начать самопроизвольно увеличиваться, так как согласно теореме Пуанкаре система должна вернуться в состояние, близкое к начальному. Однако это противоречит утверждению Н-теоремы, согласно которой функция Н не может возрастать. Основываясь на этом положении, против Н-теоремы выступил в 1896 г. Цермело⁴. Он пришел и к общему выводу, что кинетическая теория, рассматривающая всякое макротело как систему материальных точек или тел, между которыми действуют консервативные силы, не в состоянии объяснить второй закон термодинамики.

В том же году Больцман⁵, выступая против возражений Цермело, снова отметил, что Н-теорема носит вероятностный характер и не утверждает, что Н всегда обязательно убывает, а лишь указывает, что убывание этой величины наиболее вероятно. Больцман вновь привел свои рассуждения с Н-кривой и подчеркнул, что хотя система, состоящая из огромного числа материальных точек, начальное состояние которой не является равновесным, и может прийти сама собой в то же самое состояние спустя известный промежуток времени, тем не менее этот промежуток времени является чудовищно большим. Ответ Больцмана не убедил Цермело и он продолжал настаивать на противоречивости Н-теоремы. Несмотря на новые контрвозражения Больцмана, Цермело остался при своем мнении и считал, что кинетическая теория газов не объясняет явлений, связанных со вторым началом термодинамики.

Таким образом, в 90-х годах прошлого века развернулась полемика вокруг статистического толкования второго закона термодинамики. В нее включились физики, которые, основываясь на возражениях Лошмидта и Цермело, пытались доказать невозможность обоснования второго закона термодинамики с помощью молекулярно-кинетических представлений. Больцман энергично защищал свои взгляды, но был одинок. Особенно видным противником Больцмана был Мах, который, как уже неоднократно указывалось, был противником молекулярных теорий вообще. Даже в 1910 г., когда теорию Больцмана признало большинство ученых, Мах писал:

«Не могу я только отделаться от своей антипатии к гипотетически-фиктивной физике и потому имею свое особое мнение насчет исследований Больцмана касательно второго принципа на основе кинетической теории газов»⁶.

Весьма активным противником Больцмана и атомистики вообще, о чем также упоминалось, был виднейший представитель энергетизма химик Оствальд. В 1895 г. он выступил с речью, в которой нападал на атомистику. Эта речь была напечатана под названием «Несостоятельность научного материализма» и получила широкое распространение.

О ней очень резко отозвался американский физик Милликен, который, указав на успехи кинетической теории, достигнутые во второй половине XIX в., писал, что после появления сочинения Оствальда наступила реакция и что «предводимое таким бараном, все стадо овец начало обратно прыгать через забор и результаты этого попятного движения все еще чувствуются в Соединенных Штатах»⁷. В результате выступления против атомистики Маха, Оствальда и ряда других ученых в конце века стало распространяться мнение, что атомистика является уже пройденным этапом в науке, а ее основные представления устарели.

Даже многие ученые-материалисты, противники энергетики, признававшие атомистику, скептически относились к статистической теории второго закона термодинамики Больцмана. Планк, рассказывая о борьбе Больцмана с Махом и энергетиками, отмечает, что он, хотя и был активным противником последних, тем не менее не разделял взглядов Больцмана на второй закон термодинамики. Больцман, вспоминает Планк, был этим недоволен:

«Особенно неприятно ему было то,— пишет он,— что к атомистической теории, которая составляла основу всей его исследовательской работы, я относился не только равнодушно, но даже несколько отрицательно. Причина этого заключалась в том, что принципу возрастания энтропии, как и принципу сохранения энергии, я приписывал тогда применимость во всех без исключения случаях»⁸.

Только позже, к 1900 г. Планк изменил свои взгляды на второй закон термодинамики.

С начала XX столетия намечается поворот в отношении к теории Больцмана. В 1900 г. Планк, давая теоретическое обоснование открытого им закона излучения черного тела, воспользовался основной идеей Больцмана о связи энтропии с вероятностью. В 1902 г. появилась «Статистическая механика» Гиббса. В этом и следующем году вышли работы Эйнштейна по статистической механике. Начиная с 1906 г. публикуются работы П. Эренфеста, ученика Больцмана, и Т. Афанасьевой-Эренфест, в которых развивались идеи Больцмана о статистическом толковании второго закона термодинамики. В этих работах было показано, что возражения Лошмидта и Дермело основаны на непонимании существа Н-теоремы. Однако еще в 1908 г. Т. Афанасьева-Эренфест констатировала, что полемику вокруг Н-теоремы нельзя считать законченной:

«... до последнего времени одни из критиков продолжали относиться к теории Больцмана скептически или даже вполне отрицательно (в их числе автор называет имена Маха, Оствальда, Цермело, Бриллюэна и др. — Б. С.), другие же вполне с нею соглашались, но при этом, в сущности, только обходили упомянутые трудности (речь идет о трудностях, связанных с противоречием обратимости и необратимости.— Б. С.), не разрешая их вполне отчетливо»⁹.

Теория Больцмана получила признание вместе с исследованием броуновского движения. Явление броуновского движения было открыто еще в 1827 г. английским биологом Р. Броуном. Первое объяснение, которое было дано этому явлению, заключалось в предположении что непрерывное движение частиц, взвешенных в жидкости, обусловлено их органическим происхождением (первоначально это явление наблюдалось с цветочной пыльцой). Однако от такого объяснения пришлось вскоре отказаться, так как оказалось, что это явление наблюдалось и с частицами неорганических веществ. В дальнейшем была предложена гипотеза, согласно которой движение взвешенных частиц вызывается наличием конвекционных токов в жидкости. Однако и это объяснение было неудовлетворительным. После первых успехов кинетической теории теплоты в 70-х годах было высказано предположение, что движение броуновских частиц можно объяснить тепловым движением атомов и молекул. Было даже высказано мнение, что это явление противоречит второму закону термодинамики. Однако на такого рода высказывания тогда не обратили внимания.

В 1905 г. Альберт Эйнштейн в своей статье «О движении взвешенных частиц в покоящейся жидкости, требуемом молекулярно-кинетической теорией теплоты», указал на возможность использовать это явление для подтверждения кинетической теории теплоты и атомной гипотезы. В этой статье и в ряде последующих он исходил из мысли, что броуновскую частицу можно рассматривать как простую молекулу, а ее движение — как тепловое движение. Руководствуясь этой идеей и применяя методы кинетической теории теплоты, Эйнштейн вывел формулу для среднего квадрата смещения броуновской частицы, а также формулы для некоторых молекулярных констант.

Одновременно с исследованиями Эйнштейна изучением броуновского движения как явления, подтверждающего кинетическую теорию теплоты, занимался Мариан Смслуховский (1872—1917), который опубликовал первую работу «К кинетической теории броуновского молекулярного движения и суспензий» в 1906 г., а затем продолжал исследования в этом направлении. Первые же экспериментальные исследования подтвердили выводы теории броуновского движения, что явилось прямым экспериментальным подтверждением кинетической теории теплоты и атомистической гипотезы вообще.

Большую роль в подтверждении кинетической теории теплоты, а вместе с этим и гипотезы об атомно-молекулярном строении вещества сыграли экспериментальные исследования французского физика Ж. Перрена. Начиная с 1906 г. он со своими сотрудниками провел серию опытных исследований по изучению распределения по высоте взвешенных в жидкости частичек. Эти опыты показали, что закон распределения по высоте этих частичек совпадает с законом распределения по высоте молекул газа, установленным еще Больцманом. Экспериментальное подтверждение теории атомно-молекулярного строения вещества, а также кинетической теории теплоты заставило противников этой теории изменить свои взгляды и перейти на позиции этих теорий. Так, например, один из самых непримиримых противников, атомистики Оствальд уже в 1908 г. писал:

«Совпадение броуновского движения с требованиями кинетической гипотезы,,. дает теперь право самому осторожному ученому говорить об экспериментальном доказательстве атомистической теории материи. Таким образом, атомистическая теория введена в ранг научной, прочно обоснованной теории»¹⁰.

Правда, нужно отметить, что Мах до самой своей смерти, т. е. до 1916 г., продолжал отрицательно относиться к атомистике.

Вместе со всеобщим признанием кинетической теории теплоты получила, наконец, и всеобщее признание статистическая теория второго закона термодинамики Больцмана. Большую роль в этом сыграли работы М. Смолуховского по исследованию флуктуации и броуновского движения. В 1912 г. он выступил с докладом «Доступные наблюдению молекулярные явления, противоречащие обычной термодинамике», в котором, между прочим, заметил, что «лет десять тому назад было бы большим риском отзываться здесь с таким неуважением о традиционном понимании термодинамики»¹¹. Излагая теорию флуктуаций со ссылками на многие экспериментальные исследования, Смолуховский указывал:

«... В обычном понимании Клаузиуса и Томсона оно (второе начало термодинамики.— Б. С.), очевидно, не верно, так как мы видим, что небольшие тела вследствие наличия в них тепла, сами собой приходят в движение, что они производят работу против силы тяжести и магнитной силы, что сами собой появляются различия в плотности и концентрации и т. д., и величина этих флуктуаций, так же как величина молекулярных скоростей, совершенно неограниченна»¹².

Однако практически эти флуктуации весьма малы, так что их нельзя использовать для произведения макроскопической работы для того, чтобы построить вечный двигатель второго рода. В последующих работах (1912—1915) Смолуховский развил теорию флуктуаций и применил ее к целому ряду явлений, в которых «антиэнтропийное» поведение может быть наблюдаемо непосредственно. На примере этих явлений он показал, как микроскопическая обратимость может быть причиной макроскопической необратимости. Развивая идеи Больцмана, он подробно проанализировал возражения против статистического понимания второго закона термодинамики и показал ошибочность этих возражений. Смолуховский уточнил понятие «времени возврата», рассчитал это время для различных случаев. Из его расчетов, следует, что если для небольших флуктуаций это время невелико и вполне наблюдаемо, то для флуктуаций макроскопического порядка оно чудовищно велико. Таким образом, понятия обратимости и необратимости являются, по Смолуховскому, относительными и зависят от времени, в течение которого наблюдается процесс.

« Представляется ли нам какой-либо (зависящий от одного параметра) процесс обратимым или необратимым, а это ведь и является основным пунктом всего вопроса,— пишет Смолуховский,— зависит не от рода процесса, а только от начального состояния и от продолжительности наблюдения, причем все может быть выражено, простым правилом: процесс представляется нам (обратимым, необратимым), если рассматриваемое состояние обладает (длительным, кратким) временем возврата (или временем ожидания) по сравнению с продолжительностью наблюдения»¹³.

Работы Смолуховского завершили борьбу за признание статистического понимания второго закона термодинамики и окончательно решили вопрос в пользу теории Больцмана.

¹Burbury S. Nature. В. 51, 1895, S. 320.
²Boltzmann L. Wissenschaftliche Abhandlungen В. III, S. 535.
³Больцман по оси ординат откладывал не Н, а —Н.
⁴Zermelo Е. Ann. Phys. В. 57, 1896, S. 485.
⁵Boltzmann L. Wissenschaftliche Abhandlungen. В. Ill, S. 567.
⁶Мах Э. Основные идеи моей естественнонаучной теории познания и отношение к ней моих современников.— В кн.: Новые идеи в философии. Сб. 2. Спб., 1912, с. 133.
⁷Милликен Р. Новое доказательство кинетической теории материи и атомистической теории электричества.— В кн.: Философия науки. Естественнонаучные основы материализма. Ч. I. вып. II. Физика (под ред. Тимирязева А. К.). М.— Пг„ 1923, с. 148.
⁸>) Планк М. Научная биография. — Планк М. Избранные труды. М., «Наука», 1975, с. 656.
⁹Афанасьева-Эренфест Т. А.— ЖРФХО; физ. отдел., т. 40, 1908, вып. 8., с. 278.
¹⁰Оstwа1d W. Grundriss der Allgemeinen Chemie. Zeipzig, 1909, S. IV.
¹¹>) Смолуховский М. Доступные наблюдению молекулярные явления, противоречащие обычной термодинамике.— В кн.: Эйнштейн А., Смолуховский М. Броуновское движение. М.—Л., ОНТИ, 1936, с. 166.
¹²Там же, с. 193.
¹³Смолуховский М. Молекулярно-теоретические исследования по вопросу об обращении термодинамически необратимых процессов и возрасте аномальных состояний. Там же, с. 303—304.

<<Назад Вперёд>>

Просмотров: 3121

загрузка...

Другие книги по данной тематике