§ 55. Возникновение статистической механики
|
Статистическая теория второго начала термодинамики, о которой говорилось выше, развитая Больцманом, хотя и обсуждалась как всеобщая, тем не менее охватывала по существу лишь случай газов (мы исключаем при этом рассмотренные выше работы H. Н. Пирогова, в которых таких ограничений не было). Уже применение этой теории для газов, частицы которых обладают внутренним строением, а значит, и внутренним движением, требовало введения дополнительных гипотез и дополнительного рассмотрения. Больцман довольно рано обратил внимание на это обстоятельство и поставил вопрос об обобщении статистических методов, стремясь сделать их пригодными для систем более сложных, а не только для одноатомных идеальных газов. В частности, он уже в 1871 г. посвятил этому вопросу статью «Некоторое общее положение в тепловом равновесии»1, в которой был поставлен вопрос о разработке метода для нахождения средних величин для определенного вида механических систем (к этому вопросу он возвращался и в более позднее время). Основные идеи этого метода следующие. Рассмотрим систему материальных точек, состояние которой определяется п переменными s1, s2, s3,...,sn. Если составить для этой системы уравнения движения и решить их, исключив время t, то получим, как известно, п — 1 интегралов этих уравнений; пусть они будут:
φ1(s1,s2,s3,...,sn)=a1, φ2(s1,s2,s3,...,sn)=a2, ..., φn-1(s1,s2,s3,...,sn)=an-1 где a1, a2, ..., an-1 — постоянные. Если представить для наглядности n-мерное пространство с координатами s1,s2,s3,...,sn (таким представлением Больцман не пользовался), то n — 1 соотношений φ1 = a1, φ2 = a2, ..., φn-1 = аn-1 определяют в этом пространстве кривую (n — 1)-го порядка. Каждая точка этой кривой соответствует определенному моменту времени t и определяет состояние всей системы в этот момент времени. В определенных случаях состояние системы можно также определить, задавая значения какой-либо одной из переменных sk. При этом укажем определенную точку (s'1,s'2,...,s'n) на кривой в n-мерном пространстве, которая соответствует некоторому определенному состоянию системы. Однако это не всегда так. Существуют механические системы, у которых ряд переменных s1,s2,...,sk с течением времени повторяют свои значения, например, могут быть периодически или квазипериодическими функциями времени. Для таких систем одному и тому же значению переменной из этой группы соответствуют множество значений других переменных и даже непрерывная область их значений. В последнем случае кривая в фазовом пространстве, изображающая поведение нашей системы за длительный промежуток времени, почти сплошь заполнит некоторую область К в фазовом пространстве, имеющую k измерений. Другой ряд переменных sk+1, sk+2, ..., sn имеет обычный характер. Значение каждой из них однозначно определяется значением всех переменных s1,s2,...,sk и соответствующими значениями n — k интегралов системы уравнений φn(s1,s2,...,sn)=an-1, φn-1(s1,s2,...,sn)=an-1, ..., φk+1(s1,s2,...,sn)=ak+1 Таким образом, определенные значения переменных s1,s2,s3,...,sk определяют однозначно определенную точку фазовой кривой. Для таких механических систем можно говорить о суммарном времени dt их нахождения в какой-либо элементарной области ds1, ds2, ..., dsk, если рассматривать систему за очень большой промежуток времени. При этом относительное время пребывания системы в этом элементе области за значительный промежуток времени можно считать в пределе не зависящим от значений переменных s01, s02, ..., s0k в начальный момент времени t = 0. Тогда dt — относительное время пребывания системы в данном состоянии — определяет вероятность нахождения ее в таком состоянии. Пользуясь аппаратом аналитической механики, Больцман получил, что при некоторых дополнительных предположениях 
где С—постоянная, а в знаменателе стоит соответствующий якобиан. Таким образом, это время зависит только от постоянных величин, не изменяющихся со временем: от n — k интегралов и данных значений sn,sn-1, ..., sk+1,a также ds1, ds2, ...,dsk. Поэтому можно записать: dt = f(s1, s2, ..., sk)ds1ds2...dsk. Введенную функцию Больцман считает возможным рассматривать так же, как функцию распределения по фазам множества механических систем, которые являются той же самой механической системой во всевозможных состояниях, допускаемых постоянством интегралов уравнений системы, т. е. он делает первый шаг в проблеме замены распределения по времени распределением по совокупности. Полученные результаты Больцман иллюстрирует простым примером. Он рассматривает плоское движение материальной точки под действием центральной силы F=α/r2+β/r3, где 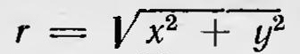 — расстояние этой точки от центра, а α и β — постоянные. Если исключить ряд частных случаев, то, вообще говоря, траектория этой точки на плоскости (х\ у) незамкнутая и должна с течением времени почти сплошь заполнить кольцевую область R {Ь ≤ r ≤ а) (рис. 14). Таким образом, определенному значению одной из координат, например координате х, соответствует не одно значение другой координаты у, а сплошной интервал таких значений. Другие переменные, определяющие состояние нашей точки, т. е. х и у, однозначно определяются значениями х, у. Это следует из того, что два интеграла движения (интеграл энергии
m/2(x2+y2)+u(x,y)=E и интеграл площадей ху — ху = М) при данных х, у однозначно определяют соответствующие х и у. В данном случае характер движения материальной точки позволяет судить о времени пребывания ее в некотором элементе плоскости dxdy за промежуток времени, настолько большой, что можно считать, что траектория почти сплошь заполняет всю кольцевую область, не учитывая начальные значения x0, y0, x0, y0. Таким образом, относительное время пребывания точки в каком-либо элементе плоскости х, х + dx; у, у + dy не зависит от начальных условий, а определяется только значениями х, у, dx, dy, и это время dt = f(x, у) dxdy. При этом f(x, у) можно рассматривать как функцию распределения точек, изображающих не одну траекторию, а целый соответствующий ансамбль таких точек.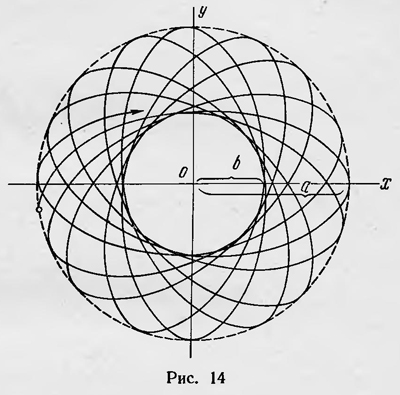 
Полученные общие результаты Больцман применяет к системе частиц, образующих нагретое тело.. При этом он впервые использует специальную гипотезу, получившую название эргодной гипотезы. Он полагает, что для такой системы, как нагретое тело, единственным однозначным интегралом движения является интеграл энергии (живых сил). Тогда все переменные этой системы, за исключением какой-либо одной, многозначны и имеют характер переменных s1, s2, ..., sk рассмотренного выше случая. Тогда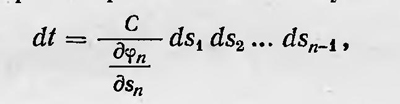 
где значение переменной sn определяется всеми остальными переменными и интегралом живых сил. Если за переменную sn принять одну из слагающих скоростей какой-либо молекулы, например, zn, то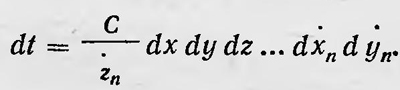 
Итак, для такой системы (эргодной системы по Больцману) получается достаточно простое выражение для dt. Это, видимо, дает возможность определить среднее значение по времени для различных физических величин, например среднее значение кинетической энергии, приходящееся на одну степень свободы, и т. д. Гипотеза, которую принял Больцман (о том, что для совокупности частиц молекул и атомов, образующих нагретое тело, существует только один интеграл движения, интеграл живых сил), равнозначна предположению о том, что с течением времени эта система проходит Есе возможные состояния, допускаемые этим интегралом. Или, иначе, точка в фазовом пространстве, которая изображает состояние нашей системы, перемещаясь по поверхности постоянной энергии Е = const, с течением времени сплошь заполняет эту поверхность: Больцман писал: «Большая неправильность теплового движения и разнообразие сил, действующих извне на тело, делает вероятным, что атомы, находящиеся в движении, которое мы называем теплотой, пробегают все совместимые с уравнением живых сил значения скоростей и положений, так что полученные выше уравнения могут быть применены к координатам и компонентам скоростей атомов тел»2. В 1879 г. в работе «О теореме Больцмана о среднем распределении энергии в системе материальных точек»3, Максвелл сделал дальнейший шаг в развитии методов статистической физики. Основная идея Максвелла, продолжавшего развивать идеи Больцмана, заключалась в возможности замены средних значений по времени средними значениями по ансамблю. Представим себе множество совершенно одинаковых консервативных систем п материальных точек, находящихся во всевозможных состояниях. Или, что то же самое, одну и ту же систему во множестве различных состояний, совместимых с постоянством энергии. Пусть N — общее число таких систем. Обозначим через dN число систем, у которых координаты q и импульсы р в момент времени t имеют «фазу» (р, q), т. е. находятся в интервале q1, q1+dq1: q2, q2+dq2;...;qn, qn+dqn; p2, p2+dp2: p3, p3+dp3;...;pn, pn+dpn. Значения импульса Pi и dpi уже не являются независимыми и определяются из условия постоянства энергии. Если ввести функцию распределения, то число систем dN, находящихся в фазе (р, q), можно записать так: dN — Nf(q1, q2, ..., qn, p2, p3, ..., pn, t)dq1...dqndp2...dpn. Спустя некоторое время (к моменту t') эти системы покинут фазу (р, q) и перейдут в новую фазу (p', q') при этом, так как число dN не меняется, f(q1, q2, ..., qn, p2, ..., pnt)dq1...dqndp2...dpqn=f(q'1, ..., qn, p'2, ..., p'n, t)dq'1...dq'ndp'2...dp'n. Согласно известному положению аналитической механики (теореме Лиувилля), имеем dq1dq2...dqndp1dp2...dpn=dq'1dq'2...dq'ndp'1...dp'n. Наши системы консервативны и обладают одной и той же энергией, поэтому, применяя уравнения Гамильтона, можно выразить dp1 и положению о том, что с течением времени эта система проходит все возможные состояния, допускаемые этим интегралом. Или, иначе, точка в фазовом пространстве, которая изображает состояние нашей системы, перемещаясь по поверхности постоянной энергии Е = const, с течением времени сплошь заполняет эту поверхность: Больцман писал: «Большая неправильность теплового движения и разнообразие сил, действующих извне на тело, делает вероятным, что атомы, находящиеся в движении, которое мы называем теплотой, пробегают все совместимые с уравнением живых сил значения скоростей и положений, так что полученные выше уравнения могут быть применены к координатам и компонентам скоростей атомов тел»4. В 1879 г. в работе «О теореме Больцмана о среднем распределении энергии в системе материальных точек»5, Максвелл сделал дальнейший шаг в развитии методов статистической физики. Основная идея Максвелла, продолжавшего развивать идеи Больцмана, заключалась в возможности замены средних значений по времени средними значениями по ансамблю. Представим себе множество совершенно одинаковых консервативных систем п материальных точек, находящихся во всевозможных состояниях. Или, что то же самое, одну и ту же систему во множестве различных состояний, совместимых с постоянством энергии. Пусть N — общее число таких систем. Обозначим через dN число систем, у которых координаты q и импульсы р в момент времени t имеют «фазу» (р, q), т. е. находятся в интервале q1, q1 + dq1; q2, q2 + dq2; ...; qn, qn + dqn; p2, p2 + dp2; p3, p3 + dp3; ...; pn, pn + dpn. Значения импульса P1 и dp1 уже не являются независимыми и определяются из условия постоянства энергии. Если ввести функцию распределения, то число систем dN, находящихся в фазе (р, q), можно записать так: dN = Nf(q1, q2, ..., qn, p2, p3, ..., pn, t)dq1...dqndp2...dpn. Спустя некоторое время (к моменту t') эти системы покинут фазу (р, q) и перейдут в новую фазу (p', q') при этом, так как число dN не меняется, f(q1, q2, ..., qn, p2, ..., pnt)dq1...dqndp2...dpn=f(q'1, ...,q'n, p'2, ..., p'n, t')dq'1...dq'ndp'2...dp'n. Согласно известному положению аналитической механики (теореме Лиувилля), имеем dq1dq2...dqndp1dp2...dpn=dq'1dq'2...dq'ndp'1dp'2...dp'n. Наши системы консервативны и обладают одной и той же энергией, поэтому, применяя уравнения Гамильтона, можно выразить dp1 и dp'1 через соответствующие скорости q1 и q'1 и энергию. Тогда получаем dq1dq2...dp2(dE)/q1=dq'1dq'2...dq'ndp'2...dp'n(dE)/q1. Сравнивая полученное равенство с условием равенства числа систем в фазах (р, q) и (р , q') и сокращая dE, имеем f(q1, ..., qn, p2, ..., pn, t)q1= f(q'1, ..., q'n, p'2, ..., p'n, t')q'1 = C, где С — постоянная величина вдоль всей «траектории», проходимой последовательно системами dN материальных точек. Рассмотрим теперь определенную совокупность систем, для которых величина С постоянна во времени для каждой данной фазы, т. е. f(q1, ..., qn, p2, ..., pn)q1 = С. Такая совокупность стационарна, а ее функция распределения является функцией только координат и импульсов и не зависит от времени. Очевидно, что в этом случае функция распределения может быть представлена как функция только интегралов движения, так как q и р должны входить в нее в таких комбинациях, которые с течением времени не меняются, а эти комбинации и есть интегралы движения Сузим теперь еще больше класс рассматриваемых систем, положив величину С не только постоянной во времени для каждой фазы, но имеющей одно и то же значение для всех фаз. В этом случае число систем dN, приходящихся на любую фазу, равно dN = C/(q1) dq1dq2...dqndp2dp3...dpn. Используя это выражение, можно определить среднее значение какой-либо физической величины, являющейся функцией координат и импульсов F(q, р), по данной совокупности систем: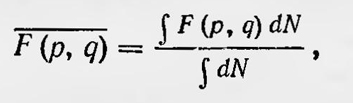 
где интегралы берутся по всем возможным значениям q и р, допускаемым условиями постоянства энергии. Полученный результат можно применить к системе атомов и молекул, образующих нагретое тело, если предположить, что эта система стечением времени принимает все состояния, допустимые постоянством энергии. Тогда для такой системы можно вычислить среднее значение по времени, наблюдаемое на опыте, заменяя его средним значением по совокупности рассмотренных ансамблей, что является гораздо более легкой задачей. Максвелл указывает, что это предположение в общем случае нельзя считать верным. Однако для систем, представляющих собой нагретое тело, вследствие хаотичности и сложности движения частиц эта гипотеза должна выполняться. Подтверждение этому Максвелл видит в правильности выводов, полученных в кинетической теории. Метод исследования, примененный Больцманом и Максвеллом и названный Максвеллом статистическим, был развит далее в работе Гиббса «Основные принципы статистической механики», опубликованной в 1902 г. В этой книге Гиббс рассматривает статистическую механику как особый раздел физико-математических наук, хотя и возникший в результате молекулярно-кинетического исследования законов термодинамики, но имеющий самостоятельное значение. В период острой дискуссии вокруг признания статистического толкования второго закона термодинамики Гиббс весьма осторожно формулирует задачи и предмет статистической механики. Ее задачей, указывает он, является статистическое исследование поведения ансамблей, состоящих из механических систем. Ансамбль — это мысленная совокупность невзаимодействующих систем, представляющих одну и ту же систему в различных (всевозможных) состояниях, т. е. обладающих всевозможными допустимыми значениями импульсов и координат. Статистическая механика, подчеркивает Гиббс, изучает такие свойства ансамблей, которые независимы от конкретного состава и строения систем, из которых они составлены. Он говорит: «... тот, кто основывает свою работу на гипотезах, касающихся строения материи, стоит на ненадежном фундаменте. Затруднения этого рода (которые возникают при использовании такой гипотезы.— Б С.) удержали автора от попыток объяснения тайн природы и заставили его удовлетвориться более скромной задачей вывода некоторых более очевидных положений, относящихся к статистической отрасли механики. При этом здесь уже не может быть ошибки с точки зрения согласия гипотез с фактами природы, ибо в этом отношении ничего и не предполагается»6. Для исследования статистического поведения ансамблей Гиббс впервые использует представление о фазовом пространстве. Состояние системы, имеющей п степеней свободы, представляется им в виде точки в 2х-мерном пространстве координат и импульсов, называемом им фазовым. Если состояние одной системы изображается в таком пространстве точкой, то весь ансамбль представляется множеством точек, сплошь заполняющих все фазовое пространство или его определенную область с некоторой плотностью D, являющейся функцией точки. С течением времени, вообще говоря, плотность в каждой точке пространства фаз изменяется. Для изменения плотности D ансамбля, состоящего из консервативных систем, Г иббс получает, пользуясь законами аналитической механики, уравнение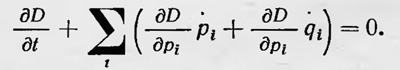 
Если ввести величину Р = D/N, где N — общее число систем в ансамбле, то это уравнение принимает вид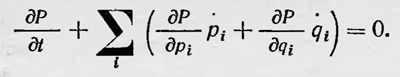 
Очевидно, что Pdq1 ...dqndp1...dpn можно рассматривать как вероятность того, что произвольная система ансамбля находится в элементе фазового пространства dq1...dqndp1...dpn. Если ансамбль находится в состоянии статистического равновесия, то D в каждой точке пространства фаз остается постоянной и δD/δt = 0 и δP/δt = 0.Уравнение тогда принимает вид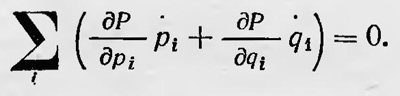 
В этом случае Р можно рассматривать как функцию только интегралов движения системы. Для дальнейшего исследования Гиббс выбирает наиболее простой случай, когда Р — функция только энергии е и имеет вид P = e(ψ-ε)/Θ, где ε и Θ являются постоянными для данного ансамбля. Такой ансамбль Гиббс называет каноническим. Изучая свойства определенных таким образом канонических ансамблей, он показывает, что они подобны свойствам нагретых тел, находящихся в термодинамическом равновесии. Так, условием статистического равновесия двух ансамблей, представляющих системы, между которыми возможно слабое взаимодействие, приводящее к обмену энергией, является условие равенства модулей распределения этих ансамблей, т.е. Θ. Таким образом, модуль распределения Θ имеет свойства, аналогичные свойствам температуры в термодинамике. Исследуя далее свойства канонических ансамблей, Гиббс устанавливает, что среднее значение показателя канонического распределения 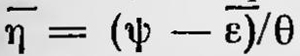 соответствует в термодинамике значению энтропии η, взятому с обратным знаком, а ψ — свободной энергии. Между 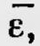 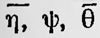 существуют соотношения
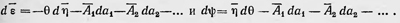
которые аналогичны обычным соотношениям в термодинамике: dU = Tdη; dψ Если потенциальная энергия каждой системы ансамбля зависит также от некоторых внешних координат а1, а2, а3.....то, введя обобщенные силы A1, А2, А3, ..., получаем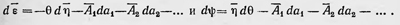 
Эти соотношения также являются аналогами термодинамических соотношений dU = Tdη — A1da1 — A2da2, dψ = -ηdT-A1da1-A2da2-..., где A1, A2 и т. д. — термодинамические параметры, определяющие наряду с Т и η состояние системы. Эти и другие полученные Гиббсом соотношения между средними имеют силу для ансамбля систем с любым числом степеней свободы п. В общем случае, если п невелико, в ансамбле число систем, которые имеют энергию, заметно отличающуюся от ее среднего значения, сравнимо с числом систем, энергия которых равна ее среднему значению. Другое дело, если имеется ансамбль, состоящий из систем с очень большим числом степеней свободы. В таком ансамбле относительное число систем, имеющих энергию, сколько-нибудь значительно отличающуюся от средней, по сравнению с числом систем, которые обладают энергией, равной средней, исчезающе мало. Исследуя этот вопрос, Гиббс разрабатывает теорию флуктуаций. Он определяет значения для выражения средней квадратичной флуктуации энергии  а также среднее значение флуктуации некоторых других величин. Он показывает, что относительные флуктуации этих величин стремятся к нулю при п → ∞.
«Таким образом,— пишет Гиббс, подводя итоги,— мы точно определили величины и строго доказали предложения, которые имеют силу для любого числа степеней свободы и которые при чрезвычайно большом числе п степеней свободы будут представляться человеческому восприятию одинаковыми с величинами и предложениями эмпирической термодинамики»7. Помимо канонического ансамбля Гиббс рассматривает также ансамбль, состоящий из систем, обладающих одной и той же энергией. Такой ансамбль получается как предельный переход от ансамбля, плотность которого во всем фазовом пространстве равна нулю, за исключением тонкого слоя, образованного двумя поверхностями энергии ε' и ε", когда разность ε' — ε" стремится к нулю. Такое распределение Гиббс называет микроканоническим. Микроканонический ансамбль более наглядно представляет нагретое тело, а свойства ансамбля — основные положения термодинамики, чем канонический ансамбль. Действительно, микроканонический ансамбль во многих случаях можно рассматривать, например, как временный ансамбль или ансамбль фаз, через которые проходит отдельная система с течением времени. Таким образом, среднее по микроканоническому ансамблю равно среднему по времени от одной системы, которое и определяется экспериментально. Однако и каноническому ансамблю можно придать более наглядный смысл. Для этого представим себе микроканонический ансамбль, образованный системой, которая имеет чрезвычайно большое число степеней свободы. Очевидно, что тогда определенную малую часть такой системы можно рассматривать как канонически распределенный ансамбль. «... Если система с большим числом степеней свободы микроканонически распределена по фазам,— пишет Гиббс,— то любая очень малая ее часть может рассматриваться как канонически распределенная»8. Следовательно, микроканоническому ансамблю можно сопоставить некий очень большой термостат, а каноническому ансамблю — некоторое малое по сравнению с термостатом тело, помещенное в нем и находящееся с ним в термодинамическом равновесии. Таков более «офизиченный» смысл канонического распределения, предлагаемый Гиббсом. Помимо нахождения средних значений по ансамблю, являющемуся моделью нагретого тела в состоянии термодинамического равновесия, Гиббс ставит перед собой задачу определить, как изменяется любой ансамбль, который не является в начальный момент времени стационарным. Нужно, очевидно, показать, что всякий ансамбль, образованный из изолированных систем, не находящийся первоначально в состоянии статистического равновесия, должен изменяться таким образом, что с течением времени он приближается к стационарному ансамблю. При этом среднее значение показателя принимает наименьшее возможное значение. Сначала Гиббс доказывает ряд теорем о максимальных и минимальных свойствах различных фазовых распределений, в частности теорему, что η имеет минимальное значение для канонического ансамбля по сравнению с любым другим ансамблем, обладающим одной и той же средней энергией. Затем, обобщая эту теорему, он указывает, что, вообще, среднее значение показателя вероятности η имеет наименьшее значение для ансамбля, у которого показатель вероятности г) является какой-либо функцией интегралов движения (функцией фазы, как их называет Гиббс) по сравнению с любым распределением, для которого среднее значение этих функций то же самое. Эти теоремы, однако, еще не показывают, как в действительности изменяется ансамбль и как, следовательно, с течением времени изменяется значение г). Более того, кажется, что, как бы ни изменялся ансамбль, состоящий из консервативных систем, значение η не должно при этом изменяться. Действительно, согласно теореме Лиувилля, одни и те же точки, которые изображают системы ансамбля в пространстве фаз, лежащие в каком-либо элементе объема этого пространства, хотя и изменяют со временем свое положение, но так, что элемент объема, занимаемый ими, перемещаясь в фазовом пространстве, не изменяет свою величину. Иными словами, совокупность точек, изображающих ансамбль, ведет себя в пространстве фаз подобно несжимаемой жидкости, так что плотность Р вдоль каждой траектории системы в этом пространстве остается все время постоянной. Следовательно, и среднее значение Р, взятое по ансамблю, не изменяется с течением времени, из чего следует, что также и среднее значение показателя вероятности η остается постоянным. Действительно, среднее значение какой-либо величины Q по определению равно Q = ∫PQdΩ, где dΩ— элемент объема фазового пространства. Поэтому η = ∫PηdΩ, но Р = = еη и η = lnP, следовательно, η — ∫PInPdΩ, т. е. η является постоянной. Однако среднее значение η можно искать другим путем, а именно: разбить все пространство фаз на мелкие ячейки, не изменяющие своего положения и своей величины в этом пространстве, и ввести так называемую крупноструктурную плотность Р, определенную уравнением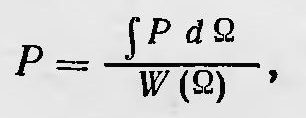 
где W(Ω) — объем ячейки, а интеграл в числителе берется по такой ячейке. Далее следует определить среднее значение для данного случая. Это среднее значение, если его обозначить через ∑, такою: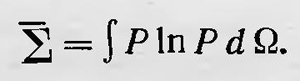 
Теперь нужно показать, что ∑Е в противоположность η не остается постоянным, а с течением времени убывает до тех пор, пока не примет наименьшее значение. Тогда ансамбль придет в состояние статистического равновесия; в частности, если при изменении ансамбля должна оставаться постоянной средняя энергия по ансамблю, то он должен стать каноническим. Сам Гиббс не доказал данное положение, а ограничился наглядным примером, поясняющим его. Рассмотрим, как и Гиббс, цилиндрический сосуд, содержащий несжимаемую жидкость; пусть в начальный момент времени жидкость, находящаяся в одном секторе, который охватывает, например, четверть окружности, окрашена в черный цвет, а остальная жидкость — прозрачная. Пусть затем жидкость приходит во вращение вокруг оси цилиндра, так что угловая скорость вращения — некоторая функция расстояния до оси. Тогда с жидкостью произойдут изменения, аналогичные имевшим место в рассмотренном выше ансамбле, т. е. хотя плотность краски в каждом малом элементе объема, перемещающемся вместе с жидкостью, с течением времени не изменяется, тем не менее краска с течением времени перемещается и плотность ее в каждом неподвижном фиксированном элементе объема будет стремиться к одной и той же величине — к равномерному распределению по всему объему. Строгая формулировка H-теоремы в теории ансамблей была дана позже (уже после смерти Гиббса) в результате работы ряда ученых4. Монография Гиббса вышла, как уже отмечалось, в 1902 г., т. е. в то время, когда борьба вокруг статистического толкования второго начала термодинамики была в самом разгаре и эта работа не могла играть сколько-нибудь существенной роли в этой борьбе. Противники статистического толкования второго начала термодинамики и атомистики вообще могли расценивать теорию Гиббса в лучшем случае как чисто абстрактную математическую теорию, не имеющую непосредственного значения для физической науки. Защитники же кинетической теории и статистического толкования второго закона термодинамики не могли найти в этой теории новых аргументов в защиту своих взглядов. Вопрос о противоречии обратимости и необратимости, вокруг которого, собственно, шла борьба, был, по существу, обойден в сочинении Гиббса. Физический смысл использования канонических ансамблей был неясен, тогда как постановка вопроса в теории Максвелла — Больцмана с физической стороны была ясной и определенной. Сторонники применения статистических методов для обоснования термодинамики рассматривали метод канонических ансамблей как искусственный математический прием, дающий возможность более легким путем получать средние значения термодинамических величин. П. и Т. Эренфесты в обзоре «Об основных статистических представлениях в механике» (1911), довольно полно характеризовавшем состояние этой области физико-математических наук, дали именно такую характеристику теории Гиббса. «С точки зрения больцмановского представления,— писали они,— введение канонического распределения является, таким образом, аналитическим приемом, подобным в некотором смысле разрывному множителю Дирихле»9. Таким же примерно образом оценивал теорию Гиббса и Смолуховский. В одном из своих докладов он говорил: «... я буду в общем следовать больше ходу мыслей Больцмана, который мне представляется стоящим ближе к физической реальности и к понятиям термодинамики, чем математически элегантный, но абстрактный метод Гиббса»10. Признание атомистической гипотезы и вместе с ней применимости статистических методов для построения молекулярно-кинетических теорий, объясняющих термодинамические закономерности, привело к необходимости подвести итог развитию новой области физических наук — статистической физики. Эту задачу в известной степени выполнили П. и Т. Эренфесты в упомянутом обзоре. Они провели анализ основных понятий и методов статистической физики и определили круг проблем, стоящих перед ней. Одной из принципиальных проблем этой области физических наук было более строгое обоснование самой возможности применения метода статистических ансамблей, разработанного Максвеллом и Больцманом, а затем и Гиббсом, к реальным механическим системам, состоящим из огромного числа частиц. Максвелл и Больцман, применяя разработанный ими статистический метод к реальным телам, основывались на эргодной гипотезе. Однако она не была ими обоснована и применялась как возможная и весьма вероятная. Эренфесты подчеркнули важность этой гипотезы для обоснования статистической механики, указав, что если бы эта гипотеза была доказана, то выводы статистической физики приобрели бы характер непреложных законов, подобных законам механики. Действительно, в этом случае среднее значение по микроканоническому ансамблю, вычисленное с помощью аппарата статистической механики, в точности равнялось бы среднему по времени, наблюдаемому в действительности. Они писали: «Если признать эргодную гипотезу, то уравнение (34) (уравнение, связывающее среднее по ансамблю и среднее по времени. — Б. С.) претендует быть чисто механической теоремой, независимой от каких-либо вероятностных представлений»11. Что касается самой гипотезы, то Эренфесты не высказывались в ее пользу и скорее даже сомневались в ее правильности. В 1913 г. Розенталь и Планшерель12 независимо друг от друга доказали невозможность существования эргодных систем. Тогда вместо эргодной гипотезы была предложена так называемая квазиэргодная гипотеза. Согласно этой гипотезе, точка, изображающая состояние системы в фазовом пространстве, хотя и не проходит через каждую точку этого пространства, лежащую на поверхности постоянной энергии, но должна с течением времени подойти сколь угодно близко к любой точке этой поверхности. На основании этой гипотезы можно также предположить равенство средних по ансамблю средним по времени. Многие физики и математики работали над доказательством справедливости квазиэргодной гипотезы и более общей проблемой доказательства равенств средних по времени средним по совокупности для статистических систем. Несмотря на то что в результате этих работ данная проблема значительно продвинулась вперед тем не менее ее до настоящего времени нельзя считать вполне решенной. 1Boltzmann L. Wissenschaftliche Abhandlungen. В. I, S. 259. 2Boltzmann L. Wissenschaftliche Abhandlungen. В. I, S. 284. 3Maxwell J. C. The scientific papers. Vol. II, 1890, p. 713. 4Boltzmann L. Wissenschaftliche Abhandlungen. В. I, S. 284. 5Maxwell J. C. The scientific papers. Vol. II, 1890, p. 713. 6Гиббс Дж. В. Основные принципы статистической механики. М.—Л., Гостехиздат, 1946, с. 14. 7Гиббс Дж. В. Основные принципы статистической механики, с. 168. 8Гиббс Дж. В. Основные принципы статистической механики, с. 181. 9Ehrenfest Р. und Т. Begriffliche Grundlagen der Statistischen Auffassung in der Mechanik. Encyklopädie der mathematischen Wissenschaften. В. IV-Т. II. Abt. II, 1914, S. 59. 10Smoluchowski M. Gültigkeitgrenzen des zweiten Hauptsatzes der Wärmetheorie, Vortrage über die kinetische Theorie der Materie und der Electricität. Zeipzig und Berlin, 1914, S. 91. 11Ehrenfest Р. und Т. Begriffliche Grundlagen der Statistischen Auffassung in der Mechanik, S. 35. 12Rosental A. Ann. Phys. B. 42, 1913, S. 796; Plancherel M. Ann. Phys B. 42, 1913, S. 1061. |
загрузка...