§ 53. Развитие молекулярно-кинетического толкования второго закона термодинамики
|
Проблема молекулярно-кинетического обоснования второго начала термодинамики возникла одновременно с установлением самого закона. Вначале исследователи пытались найти обоснование этого закона в каких-то особенностях механического движения атомов и молекул, вывести, если можно так сказать, этот закон, применяя к системе материальных точек, представляющих нагретое тело, законы механики. Первые попытки в этом направлении были предприняты Ранкином в работах, посвященных исследованиям по термодинамике и кинетической теории, о которой мы уже упоминали. Исходя из гипотезы, что тепловое движение имеет «вихревой» характер, он старался объяснить и второй закон термодинамики. В 1865 г. в работе «О втором законе термодинамики» Ранкин ставил задачу:
«... дать доказательство того, что второй закон термодинамики вытекает из предположения, что ощутимое тепло заключается в некотором роде устойчивом молекулярном движении внутри ограниченного пространства»1. Опираясь на эти предположения и применяя законы механики, Ранкин с помощью дополнительных гипотез получил нечто подобное второму началу термодинамики для обратимых процессов, т. е. установил факт существования энтропии. Однако последовательную теорию Ранкин разработать, конечно, не смог. Общая идея объяснения второго закона термодинамики с помощью подобного рода представлений о характере теплового движения была развита Больцманом в 1866 г. в его работе «О механическом значении второго закона теории тепла». Больцман полагал, что как первый закон термодинамики, являющийся законом сохранения живых сил, так и второй закон должен иметь в своей основе некоторое общее положение механики. «Цель настоящей работы,— писал Больцман,— заключается в том, чтобы дать чисто аналитическое, вполне общее доказательство второму закону теории тепла, отыскав для него соответствующее положение механики»2. В качестве такого положения механики Больцман считает возможным взять принцип наименьшего действия в несколько обобщенной форме. Представим себе нагретое тело как систему материальных точек — атомов и введем гипотезу, что каждый из этих атомов, находясь в тепловом движении, движется по замкнутой траектории. При этом если данное тело находится в состоянии термодинамического равновесия, то период обращения всех атомов по своим траекториям один и тот же. Будем сообщать теперь нашему телу некоторое малое количество тепла AQ настолько медленно, что можно считать в каждый данный момент времени состояние тела стационарным или равновесным. В результате такого очень медленного процесса каждый атом тела получит некоторое малое количество энергии Δq и перейдет с первоначальной замкнутой траектории на бесконечно близкую к ней и также замкнутую траекторию. Определим изменение действия при переходе атома с одной траектории на другую. Для этого возьмем вариацию действия 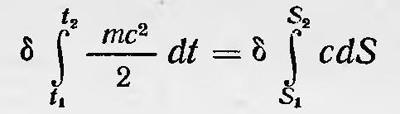
с учетом вариации пределов S1 и S2. В результате довольно длинных преобразований вариации этого интеграла получим, что 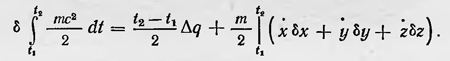
Траектория атома замкнутая, и атом в моменты времени t1 и t2 имеет одно и то же положение, а также одну и ту же скорость (t2 — t1 — период обращения), поэтому последний член в выражении для вариации действия пропадает, следовательно, 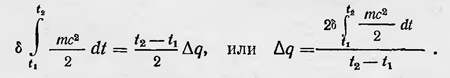
Разделив обе части последнего равенства на выражение температуры Т, полагая, что она равна среднему значению кинетической энергии каждого атома, т. е. 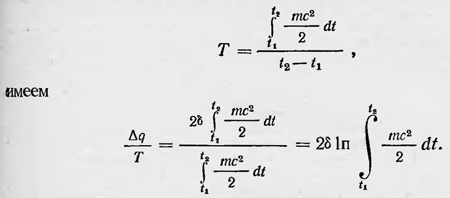
Учитывая далее, что все количество тепла ΔQ равно ∑Δqi, где сумма берется ко всем атомам, а также что период обращения у всех атомов один и тот же, получим окончательно 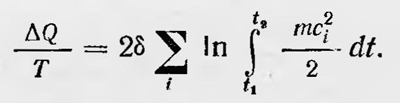
Но ΔQ/T есть не что иное, как изменение энтропии S в процессе сообщения количества тепла ΔQ нашей системы, а выражение, стоящее справа, — полный дифференциал, поэтому последнее равенство можно интерпретировать как выражение второго закона термодинамики для обратимых процессов: 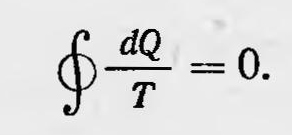
Получив этот результат, Больцман считал, что он наметил механическое толкование второго закона термодинамики для обратимых процессов. Что же касается необратимых процессов, то он приводит ряд общих соображений, которые должны, по его мнению, показать возможность получения для необратимых процессов 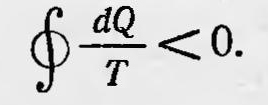
Пытаясь освободиться от искусственного предположения о тепловом движении, согласно которому все атомы двигаются по замкнутым траекториям с одним и тем же периодом, Больцман считал, что нужно лишь допустить, что особенностью теплового движения является условие равенства нулю величины 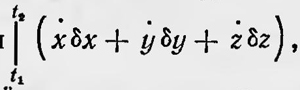 , входящей в выражение вариации интеграла действия, а это, по его мнению, весьма вероятно. , входящей в выражение вариации интеграла действия, а это, по его мнению, весьма вероятно.
В конце работы Больцман пишет: «... наше заключение совершенно независимо от смысла величин, встречающихся в учении о теплоте, и поэтому представляет собой теорему чистой механики, которая соответствует второму закону, так же как принцип живых сил — первому. Она и выражает, как показывает наш вывод, принцип наименьшего действия, однако в несколько обобщенной форме, в которой он может быть выражен примерно так: Если система точек совершает любое движение под действием сил, для которых действителен принцип живых сил, и если всем точкам сообщается бесконечна малая живая сила и они вынуждены двигаться по бесконечно близким кривым, то 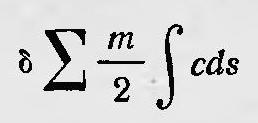
равна сумме сообщенных живых сил, умноженных на половину времени, в течение которого рассматривается движение, если суммы произведений перемещений точек и скоростей и косинусов углов для обеих границ равны»3. Спустя несколько лет, по-видимому независимо от Больцмана, Клаузиус пришел к той же идее о возможности механического обоснования второго закона термодинамики. Соответствующую теорию Клаузиус опубликовал в 1871 г. Он писал, что ставит перед собой задачу «найти объяснение этому уравнению (речь идет о математическом выражении второго начала термодинамики. — Б. С.), основанное на механических принципах»4. Постановка задачи у Клаузиуса более общая, нежели у Больцмана, и гипотезы, на которые он опирался, менее искусственны, чем у последнего. Клаузиус не предполагал, что все атомы совершают замкнутые траектории с одним и тем же периодом. Для его доказательства достаточно было принять, что слагающие скорости каждого атома через определенные промежутки времени (периоды) меняют знак. Эти периоды для различных атомов могут различаться, но существуют группы атомов с одним и тем же периодом изменения слагающих скоростей. Заключая свою работу, Клаузиус пишет: «Предыдущий вывод показывает, как полученный закон, а вместе с ним и второй принцип механической теории тепла, основываются на общем механическом принципе»5. В дальнейшем некоторые физики, следуя Больцману и Клаузиусу, в том числе и сам Клаузиус, пытались усовершенствовать вывод второго закона термодинамики, исходя из принципов механики. Дадим общее представление об этих попытках (в несколько модернизированном виде). Рассмотрим систему n материальных точек. Пусть в момент времени t1 положение их представлено точкой S1(x'1, у'1, z'1, ..., х'n, у'n, zn') в 3х-мерном пространстве, а в момент времени t2 — точкой St1(x"1, у"1, z"1, ..., х"n, у"n. Запишем действие для этой системы за время Δ = t2 — t1. Имеем 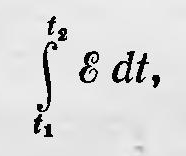
где ε — кинетическая энергия всех точек, а интеграл берется по траектории S1,S2. Вычислим вариацию этого интеграла за тот же промежуток времени при изменении траектории S1S2 на траекторию S1 + dS1, S2 + dS2, бесконечно близкую к первой. Выражая ε как функцию скоростей и интегрируя по частям, получаем: 
где U — потенциальная энергия всех сил, действующих на материальные точки. Пусть теперь потенциальная энергия является функцией не только координат всех материальных точек m1, m2,...mn, но также и некоторых внешних параметров c1, c2,..., cx,...; тогда 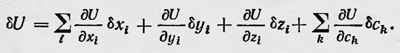
Величину 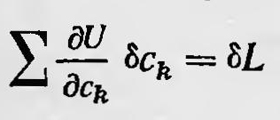 можно рассматривать как работу, совершаемую нашей системой материальных точек против внешних сил. Учитывая сказанное, получаем можно рассматривать как работу, совершаемую нашей системой материальных точек против внешних сил. Учитывая сказанное, получаем
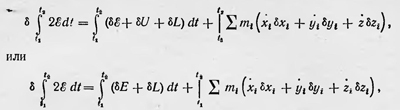
где Е — полная энергия системы6. Теперь применим полученное соотношение, которое представляет собой простое преобразование вариации действия, к системе материальных точек — атомов и молекул, представляющей нагретое тело. Для этого прежде всего нужно перейти к средним значениям величин, стоящих в выражении для вариации действия. Среднее значение какой-либо величины А за время τ = t2 — t1 равно 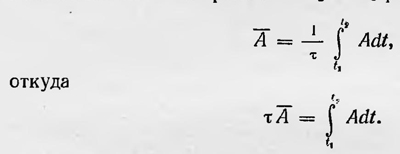
Принимая во внимание последнее равенство, можно записать выражение для вариации действия за время τ = t2 — t1 в виде 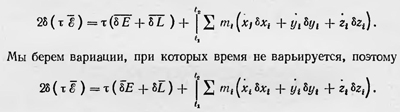
Теперь следует сделать предположение о характере теплового движения. Во-первых, возможно такое состояние движения системы, при котором средняя общая энергия ее остается постоянной, а внешняя работа в среднем не производится. Причем это справедливо для любого времени т, лишь бы только время τ было достаточно малым по сравнению со временем, в течение которого производятся макроскопические измерения, и достаточно велико по сравнению со временем протекания микропроцессов. Возможность такого состояния естественно предполагается при всех подобных выводах второго начала термодинамики. Это состояние является не чем иным, как состоянием термодинамического равновесия, когда оно, несмотря на разнообразие микродвижений, характеризуется с макроскопической точки зрения постоянными термодинамическими величинами: определенной температурой, величиной внутренней энергии и внешними параметрами, такими, как объем и т. д. Сообщим теперь нашей системе, находящейся в состоянии термодинамического равновесия, некоторое бесконечно малое количество тепла Q. В результате средняя внутренняя энергия системы изменяется в среднем на величину б Е, а также производится в среднем внешняя работай L и тело перейдет в новое бесконечно близкое состояние термодинамического равновесия. Этот действительный процесс можно сопоставить и заменить мысленным процессом, представляющим собой процесс вариации средних величин выражения, полученного при усреднении вариации действия. Учитывая, что согласно молекулярно-кинетической теории температура тела Т пропорциональна среднему значению кинетической энергии его молекул или атомов и чтоб Ē + δ L=δQ, получим 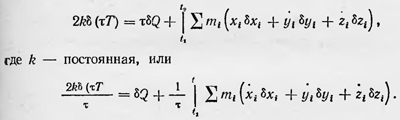
Теперь сделаем еще одно предположение о характере теплового движения. Положим, что последний член в данном равенстве пропадает; тогда 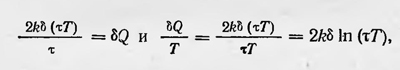
что и является математическим выражением второго начала термодинамики для обратимых процессов. Действительно, из него следует, что величина δQ/T полный дифференциал некоторой функции, т. е. 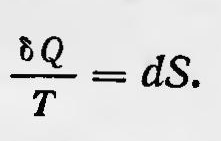
Последнее предположение о характере теплового движения в отличие от предположения о возможности существования состояния термодинамического равновесия и т. д. далеко не очевидно и требует обоснования. Первоначально Больцман, как уже говорилось, полагал, что все частицы тела, находящиеся в тепловом движении, в случае термодинамического равновесия совершают периодические движения по замкнутым траекториям. Тогда очевидно, что сумма 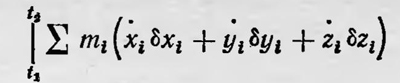
в случае, если t2 — t1 = τ равно периоду или времени, кратному периоду обращения, равна нулю. Однако такое представление слишком неправдоподобно, и сам Больцман уже в первом доказательстве пытался его обобщить. Клаузиус вводит более общее предположение, о котором также говорилось. Имели место и еще более общие предположения. При этом все шире и шире опирались на вероятностные статистические соображения, полагая, например, что эта сумма исчезает в среднем в результате сложности движения атомов. Больцман специально впоследствии подчеркивал это. Он писал: «Для случая, когда каждый атом движется по замкнутой траектории, я уже определил в представленном академии в 1866 г. исследовании величину, дифференциал которой есть δQ/T. Если, однако, траектории атомо и не являются замкнутыми, то пока вероятности различных положений атомов не определены, можно найти случаи, когда δQ/T не является полным дифференциалом. Следовательно, строгое распространение доказательства на этот случай возможно лишь при рассмотрении этих вероятностей»7. Но если аргументация из области теории вероятностей в какой-то мере спасала положение с выводом второго начала термодинамики из общих принципов механики для случая обратимых процессов, то все попытки распространить этот вывод на случай необратимых процессов оказались безуспешными и авторы подобного рода доказательств были вынуждены обращаться либо к общим, совсем не очевидным, положениям, либо к доводам из области чистой термодинамики. К 80-м годам в литературе появляются высказывания о безуспешности таких попыток. В своей работе «Второй закон термодинамики с точки зрения аналитической механики и теории вероятностей» (1883) русский физик В. А. Михельсон, проанализировав существовавшие выводы второго закона термодинамики из общих принципов механики и предложив свой (один из наиболее общих) вывод, подчеркнул: «... для необоротных процессов на чисто механической почве еще ни один автор не провел этого исследования, да и на основании некоторых соображений Больцмана о зависимости второго закона от теории вероятностей можно заключить, что оно вообще вряд ли возможно без приемов последней»8. Соображения Больцмана, о которых говорит Михельсон, и были теми основными теоретико-вероятностными положениями, на основе которых он уже к этому времени начал строить свое молекулярнокинетическое обоснование второго начала термодинамики. Больцман постепенно пришел к выводу о чисто статистическом характере второго закона термодинамики. Сначала, как мы видели выше, он предполагал дать ему чисто механическое толкование. Но затем он все яснее и яснее начал понимать, что без теоретико-вероятностных положений с точки зрения молекулярных представлений этот закон истолковать нельзя. И, наконец, он пришел к выводу о чисто статистическом смысле этого закона. В работе «Дальнейшее исследование теплового равновесия», (1872), а затем в более общем виде в работе «О тепловом равновесии газа, на который действуют внешние силы» (1875), Больцман впервые изложил статистическое толкование второго закона термодинамики. В начале первой работы он подчеркнул, что вследствие огромного числа молекул, составляющих тела макроскопических размеров, и чрезвычайной быстроты и беспорядочности их движения мы наблюдаем лишь средние значения, которые как раз в результате этого остаются постоянными при постоянстве макроскопических условий, в которых находится тело. Определение же средних значений — задача теории вероятности, «поэтому проблемы механической теории тепла являются проблемами теории вероятностей»9. Больцман рассматривает простую модель газа, состоящию из упругих шариков — молекул, взаимодействующих в результате упругих соударений и находящихся в поле потенциальных сил. Состояние газа определяется функцией распределения f, которая зависит от положения молекул х, у, z, их скоростей х, у, z, а также и от времени t. Функция распределения f может быть любой, но такой, чтобы она имела один и тот же вид для всякого малого с макроскопической точки зрения объема, содержащего очень много молекул газа. Для функции распределения Больцман выводит уравнение, получившее название кинетического уравнения, которое имеет вид 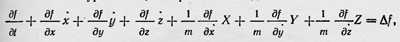
где X, У, Z — компоненты сил, действующих на молекулы газа, Δf — изменение функции распределения f в результате соударений, происходящих между молекулами. Величина Δf сложным образом зависит от размеров молекул, их взаимного расположения и скоростей. Для ее определения Больцману приходится ввести предположение, которое сводится к гипотезе о статической независимости положения и скорости каждой молекулы от координат и скоростей всех других молекул (гипотеза элементарного беспорядка). Принципиальная важность этой гипотезы, ее противоречие законам механики — все это стало вполне ясно позже, в процессе дискуссии о статистическом обосновании второго закона термодинамики. Чтобы решить вопрос о виде функции распределения в случае термодинамического равновесия, нужно, очевидно, положить, что δf/δt. Это условие при отсутствии силового поля, когда X — Y = Z = = 0, дает Δf = 0, а последнее уравнение однозначно приводит к закону распределения скоростей Максвелла. В более сложном случае, если молекулы газа находятся в силовом поле, имеющем потенциал, получается, что стационарному состоянию соответствует распределение Максвелла — Больцмана. В общем же случае не равно нулю и функция распределения должна изменяться. Больцман ставит перед собой задачу показать, что с течением времени она все больше и больше приближается к функции, описывающей состояние статистического равновесия, т. е. к функции распределения Максвелла — Больцмана. Для этого он рассматривает величину Е = ∫flnfdω, где dω = dxdydzdxdydz, а интеграл берется по всем возможным значениям х, у, z, х, у, z, и доказывает теорему, что δЕ/δt≤0, т. е. величина Е может только уменьшаться с течением времени или, приняв минимальное значение, оставаться постоянной. В последнем случае оказывается, что эта функция становится функцией распределения Максвелла — Больцмана. Таким образом, Больцман доказал, что газ, находящийся сначала в состоянии, отличном от состояния статистического равновесия, стремится перейти в это состояние, описываемое распределением Максвелла — Больцмана. Теорема Больцмана, названная первоначально минимум-теоремой, затем была переименована в Н-теорему, так как приведенный выше интеграл получил обозначение Н. Теперь было естественно связать величину Я с энтропией, а доказанную теорему рассматривать как выражение второго закона термодинамики, тем более что простой расчет показывает, что Я для идеального газа в случае статистического равновесия просто пропорциональна величине энтропии, взятой с обратным знаком. Больцман так и рассматривает свою Н-теорему. Он пишет, что «... для атомных движений очень большого числа материальных точек всегда существует некая иеличина, которая вследствие диижений атомов не может увеличиваться, и эта величина с точностью до постоянного множителя соответствует той, которую я нашел для известного интеграла ∫dQ/T в моей работе «Аналитическое доказательство второго закона термодинамики». И далееі «Вместе о этим это есть аналитическое доказательство второго закона термодинамики, построенного на совсем ином пути, чем это до сих пор было. До сих пор всегда искали доказательство того, что ∫dQ/T для обратимых процессов, что, однако, не являлось аналитическим доказательством этого закона для необратимых круговых процессов, которые тем не менее всегда происходят в природе, в то время кан обратимые процессы являются лишь идеализацией ... Здесь же мне удалось прямо получить, что всегда отрицателен и только для граничного случая равен нулю, что соответствует обратимым процессам»10. На теорию Больцмана первоначально обратил внимание только Лошмидт, который в 1876 г. сделал некоторые замечания по поводу этих работ11. Одно из замечаний имело принципиальное значение и известно как парадокс или возражение Лошмидта против Н-теоремы Больцмана. Смысл его заключается в противоречии между законами механики и вторым законом термодинамики, что указывает на невозможность объяснения второго закона термодинамики на основании законов механики. Если представить себе нагретое тело как систему материальных точек и если, например, за время t эта система изменяется в направлении уменьшения величины Н и соответственно увеличения энтропии, то, если в конце этого промежутка времени изменить все скорости частиц на обратные, изменение системы должно происходить теперь в обратном направлении: величина Н должна увеличиваться, а энтропия — убывать. И если, например, изменить направление скоростей всех частиц во Вселенной, то все процессы в мире должны пойти в обратном направлении и энтропия мира должна убывать. Больцман специально остановился на замечаниях Лошмидта. Больцман отмечал, что Лошмидт прав, полагая, что если в системе многих материальных точек изменить скорости на обратные, то изменение системы будет происходить обратным путем, и если до этого энтропия возрастала, то теперь она будет убывать. Но это не противоречит Н-теореме, которая указывает лишь на наиболее вероятное течение процессов. Отвечая Лошмидту, Больцман считает необходимым подчеркнуть чисто вероятностный и статистический смысл второго закона термодинамики и намечает новый подход для его обоснования. Этот подход заключается в расчете вероятности различных состояний системы материальных точек, образующих идеальный газ, и доказательстве, что наиболее вероятное состояние этой системы такое, при котором ее Энтропия наибольшая. Он пишет: «Можно даже рассчитать из отношения числа различных распределений состояний (Zustandsverteilung) их вероятность, что, возможно, приведет к интересному методу расчета теплового равновесия. По крайней мере для некоторых специальных случаев удается доказать, что когда система переходит от неравно-отрицательным и, наоборот, положительным в противоположном случае, Так как существует бесконечно большее число равномерных распределений состояний, чем неравномерных, то последний случай является в высшей степени невероятным и практически может рассматриваться как невозможный»12. Эти идеи Больцман развивает в том же 1877 г. Изложим их кратко в модернизированном виде, применяя другие обозначения, нежели Больцман, однако не изменяя существа его рассуждений. Больцман полагает теперь, что все состояния частиц газа, определяемые координатами и слагающими скоростей или импульсов, равновероятны. Конкретно это выражается в том, что вероятность частицы находится, говоря современным языком, в элементе фазового объема dω = dxdydzxdxdydz, определяется единственно величиной этого элемента и с точностью до постоянного множителя просто равна ему. Тогда состояние всей системы, при котором n1 определенных частиц находятся в элементе фазового пространства dω1, n2 определенных частиц — в элементе dω2 и т. д., имеет вероятность 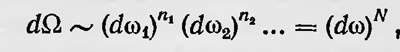
где N — общее число частиц. Для термодинамического состояния системы, однако, безразлично, будут ли в элементе фазового объема dω1 находиться частицы, имеющие, например, номера 1, 2, 3, ..., в элементе dω2— частицы с номерами 10, 11, ... и т. д. или какие-либо другие. Таким образом, какому-нибудь определенному термодинамическому состоянию системы соответствуют Z определенных микросостояний и вероятность такого термодинамического состояния, если учитывать, что вероятности всех микросостояний одинаковы, будет пропорциональна 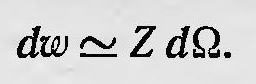
Таким образом, для того чтобы определить величину вероятности ω, нужно определить величину Z, число микросостояний, соответствующих одному макросостоянию, или, говоря современным языком, статистический вес этого состояния13. Величина Z определяется по правилам комбинаторики: 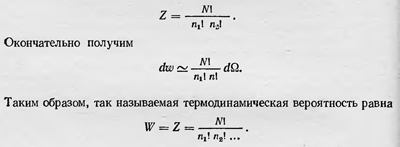
Чтобы упростить это выражение, Больцман предполагает, что все n1, n2, ..., как и N, — очень большие числа. Это означает, что он выбирает такие элементы фазового объема dω, которые хотя и малы, но содержат большое число частиц n1, n2, n3, .... Тогда для вычисления значения W можно приближенно считать, что14 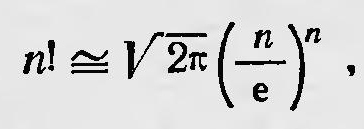
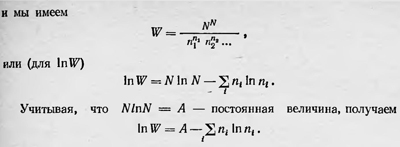
Определим теперь, какое термодинамическое состояние имеет наибольшую вероятность. Это, очевидно, такое состояние, для которого W, а значит и lnW, имеет максимальное значение при условии постоянства числа частиц N и их общей энергии Е. Задача, таким образом, сводится к нахождению максимума величины - ∑inilnni при условиях 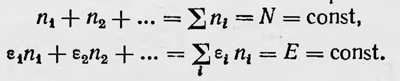
Здесь ε1 — энергия частицы, находящейся в і-м элементе фазового объема. Если учесть, что ni = f(xi, yi, zi, vx, vy, vz)dω, или, кратко, ni = fidomega;i, и заменить сумму интегралом, то задача сводится к нахождению максимума интеграла — ∫ωlnfdω при условиях ∫ωfdω= const, ∫ωεfdω = const. Решение этой задачи определяет вид функции распределения для наиболее вероятного состояния идеального газа. Этой функцией является функция распределения Максвелла — Больцмана. Далее, выражение для lnWc точностью до постоянной равно величине Н, взятой с обратным знаком, которая, в свою очередь, пропорциональна энтропии идеального газа. Обобщая эти результаты, Больцман приходит к заключению, что между термодинамической вероятностью всякого состояния газа и его энтропией в этом состоянии существует простая зависимость, а именно: энтропия S пропорциональна логарифму термодинамической вероятности: S≈lnW. Тогда стремление газа к состоянию с максимальной энтропией есть не что иное, как стремление к наиболее вероятному состоянию. В заключение Больцман высказывает мысль о том, что хотя подобное соотношение между вероятностью и энтропией для жидких и твердых тел пока еще не доказано, однако есть все основания полагать, что оно имеет универсальный характер. Таким образом, Больцман пришел к совершенно новому толкованию второго закона термодинамики. Теперь этот закон понимается им как чисто статистический закон, целиком основанный на теории вероятности. В 1886 г. в докладе «Второй закон механической теории тепла» он говорил: «... каждому распределению энергии соответствует количественно определяемая вероятность. Так как она в практически важнейших случаях совпадает с величиной, названной Клаузиусом энтропией, то мы считаем нужным обозначить ее тем же названием»15. 
Первоначально работы Больцмана, посвященные статистическому толкованию второго начала термодинамики, не обратили на себя внимания ученых. Идея о возможности вывести второе начало термодинамики на основе общих принципов механики, эклектически сочетая статистические представления и принцип наименьшего действия (или какой-либо более общий принцип, выводимый из начал аналитической механики), еще не потеряла своих приверженцев. Так, венгерский ученый Сцили в 1877 г. пытался вновь дать подобный вывод. В 1882 г. такую попытку повторил Оппенгейм. В 1883 г. Михельсон в упоминавшейся уже работе предложил свой вариант такого доказательства. Правда, он подчеркивал, что для необратимых процессов такие попытки, вероятно, обречены на неудачу и уже ссылался на работы Больцмана. Однако интересно отметить, что работа Михельсона не была полностью опубликована. В печати появилась только та ее часть, в которой он рассматривал доказательство второго закона на основании принципов аналитической механики. В 1884 г. Гельмгольц в исследовании «Начала статики моноциклических систем» сделал новую попытку связать второй закон термодинамики с общими принципами механики, применяя их к специальным механическим системам, названным им моноциклическими. Моноциклической механической системой он называл систему, у которой одна координата меняется очень медленно, все остальные совершают быстрые циклические движения. Гельмгольц показал, что для моноциклической системы можно получить соотношения, аналогичные второму закону термодинамики для обратимых процессов. Простейшим примером моноциклической системы является обычный центробежный регулятор (рйс. 12). Если он вращается с постоянной угловой скоростью и ему очень медленно сообщить некоторое количество энергии δQ, то при этом изменяется его кинетическая энергия вращения δТ и будет произведена работа δА в результате подъема грузиков регулятора, так что δQ = δТ + δА Можно показать, что для данного случая, если через т обозначить период вращения диска, справедливо соотношение 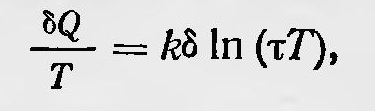
аналогичное выражению второго закона термодинамики для обратимых процессов. Гельмгольц пишет, что его работа «... преследует цель доказать, что существует класс механически вполне определенных движений, для которых имеет место ограничение превращаемости рабочих эквивалентов, подобно тому, как второе начало дает такое ограничение для теплового движения»16. Правда, по мнению Гельмгольца, между тепловым движением и свойствами моноциклических систем существует лишь аналогия, и он не претендует «дать объяснение второму закону механической теории тепла», тем не менее придает важное значение такого рода исследованиям в раскрытии существа второго закона термодинамики. Для указанных статей Гельмгольца характерно, что он даже не упоминает работы Больцмана по статическому обоснованию второго начала термодинамики. Хотя прошло уже более десяти лет после выхода в свет работы Больцмана, в которой была доказана Н-теорема, и более пяти лет после появления работы, в которой он дал чисто вероятностное толкование этому закону, тем не менее Гельмгольц не касается этих работ, а ссылается на работы Больцмана и Клаузиуса, посвященные попыткам доказать второй закон термодинамики на основе общих принципов механики. Уже позже, в 1894 г., А. Г. Столетов, сравнивая статистический вывод второго закона термодинамики, данный Больцманом, с идеями Гельмгольца, отдает предпочтение последним: «Гельмгольц берет задачу проще, общнее и отчетливее» — и указывает далее, что в работах Гельмгольца была «построена весьма общая механическая модель того, что мы называем теплым телом»17. Таким образом, работы Больцмана, посвященные статистическому толкованию второго начала термодинамики, оставались малоизвестными и даже просто игнорировались. На них не обращали сколько-нибудь серьезного внимания, так как сама мысль, что один из самых общих законов природы —второй закон термодинамики — является законом простого случая, не могла не показаться подавляющему большинству ученых того времени по меньшей мере странной. Можно назвать, пожалуй, только русского физика Николая Николаевича Пирогова (1843—1891), который (вслед за Больцманом) работал над задачей статистического обоснования второго закона термодинамики. H. Н. Пирогов (сын известного русского хирурга Н. И. Пирогова) уже в зрелом возрасте занялся теоретическими исследованиями по физике. Все его работы были посвящены кинетической теории газов и статистической физике и напечатаны в «Журнале Русского физикохимического общества» в период с 1885 по 1891 г. Пирогов уделил большое внимание статистическому обоснованию второго закона термодинамики18. Главная работа, посвященная этому вопросу («О законе Boltzmanna»), был а напечатана в 1890 г.19. Для статистического обоснования второго закона термодинамики Пирогов разработал специальный математический аппарат, идеи которого, если их изложить, в современных понятиях и в несколько модернизированной форме, сводились к следующему . Рассмотрим последовательность, А, состоящую из большого числа N чисел, расположенных в возрастающем порядке x1, x2,... . Пусть для любых двух последовательных чисел этой последовательности xk и xk+1 можно принять, что xk+1 - xk+ = Δxk<ε, где ε — очень малая положительная величина, т. е., по терминологии Пирогова, последовательность А является «почти сплошной». Назовем интервал Δxk сопряженным интервалом члена последовательности и определим функцию F(x) условием 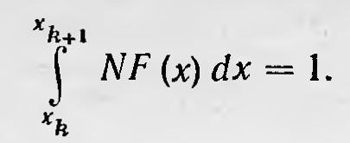
Полагая, что функция F(x) непрерывна, и учитывая, что сопряженные интервалы чрезвычайно малы, можно с достаточной степенью точности записать это условие в виде NF(х)Δxk = 1. Очевидно, что функцию F(x) можно считать функцией распределения числа членов последовательности А и число их в интервале xm, xi таково: 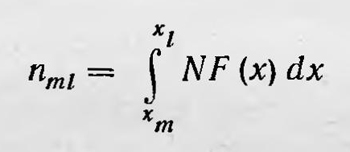
при условии, что интервал xm, xi включает по крайней мере один из сопряженных интервалов. Разделим теперь каждый интервал Δxk на равные, еще более малые интервалы величиной γ так, что γ << Δxk. Число таких отрезков в интервале Δxk равно qk = Δxk/γ. Если теперь каждый член последовательности xk получит приращение μγ, где μ ≤ qk, то мы получим новую последовательность, которая по-прежнему изображается той же самой функцией распределения F(x). Таким образом, число последовательностей, изображаемых одной и той же функцией распределения, очевидно, равно 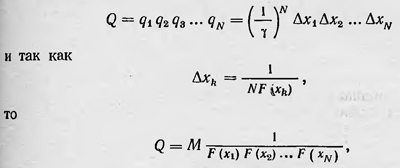
где М = 1/(γN)N — постоянная, определяемая лишь числом членов последовательности и величиной интервала γ. Таким образом, всякой функции распределения соответствует определенное число последовательностей, изображаемых одной и той же функцией. Это число с точностью до постоянного множителя равно 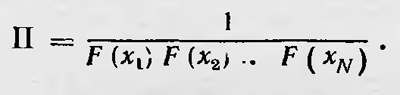
Величину II Пирогов называет «тропометрической» величиной последовательности А. Логарифм этой величины S, если его выразить с помощью интеграла, равен 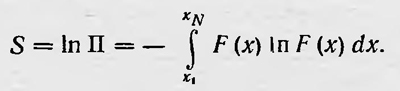
Произведем теперь определенную операцию над членами некоторой первоначальной последовательности А1 изображаемой функцией распределения А1(х), которую Пирогов называет «варьированием» последовательности. Пусть все ее члены получают некоторые приращения δх1, δх2,δх3, ..., δхN; в результате последовательность А1 превратится в новую, члены которой х'1, х'2, х'3, ..., х'N, соответственно равны х1 + + δх1, х2 + δх2, ..., хN + δхN. Приращения δх1, γδх2, δх3, ... могут быть любыми, но всегда кратными γ, так что 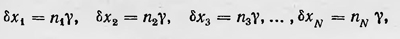
где n1, n2, ..., nN — целые числа. Изменим всевозможным образом n1, n2, n3 ..., nN от 0 до n; причем n — весьма большое число. Тогда в результате такого варьирования последовательности А1 получим множество других последовательностей; пусть их будет Р. Очевидно, что среди Р последовательностей существует рi таких, которые по-прежнему изображаются функцией распределения F1(х), p2 — функцией F2(х), p3 — функцией F3(x) и т.д. При этом Р = p1+p2+p3... . Полагая, что все вариации членов последовательности равновероятны, приходим к заключению, что вероятность при таком всевозможном варьировании членов последовательности А1 получить ту, которая изображается функцией распределения Fi(x), равна pi/P, где pi — число последовательностей, изображаемых этой функцией распределения Fi(x). Но если вероятность всякой последовательности, изображаемой Fi(x), определяется числом рi, соответствующим этой функции, то наибольшую вероятность имеет та последовательность, для которой это число наибольшее, а значит, и тропометрическая величина и ее логарифм Si имеют наибольшие значения. Таким образом, наивероятнейшей из всех последовательностей, которые получены в процессе варьирования, определенного выше, является последовательность, изображаемая функцией распределения Fi(x), для которой Si = 1пПi имеет наибольшее значение. Как же в действительности изменяется последовательность А1 в результате случайного варьирования ее членов? Очевидно, что если каждый член этой последовательности получит лишь одно случайное приращение, то можно подсчитать вероятность его изменения в том или ином направлении и вероятность изменения функции распределения Fi(x), соответствующей этой последовательности, в какую-либо другую функцию. Дело, однако, обстоит иначе, если каждый член последовательности А1 получит много очень весьма малых случайных приращений, т. е. если вновь полученная в результате многократного варьирования последовательность имеет члены 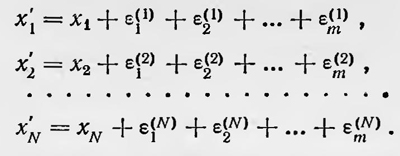
В этом случае с очень большой вероятностью при любых вариациях ε1)(γ), если они достаточно малы и число их достаточно велико, первоначальная последовательность Аг превратится в другую определенную последовательность А2, для которой S2 > S1. Причем вероятность эта стремится к единице, когда каждое приращение ε1)(γ) стремится к нулю, а число их m стремится к ∞. Таким образом, если первоначальную последовательность А1 подвергнуть такому случайному многократному варьированию, то в результате с очень большой вероятностью, в пределе стремящейся к единице, будем получать совершенно определенные новые последовательности А2, А3, A4, ... и т. д., которые изображаются функциями распределения F2(x), F3(x), F4 (х), ..., так что при этом величина S все время возрастает, т. е. S1 Это предположение, сделанное Пироговым, правильно. Его не трудно обосновать. Действительно, процесс многократного варьирования, которым он пользуется, аналогичен стохастическому процессу так называемых случайных блужданий точек, имеющих первоначально координаты, численно равные х1, х2, х3, ..., xN вдоль прямой. Если рассматривать функцию распределения как функцию координат х и времени t, то известно, что в этом случае она удовлетворяет уравнению диффузии 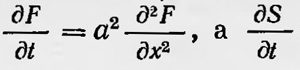 , а в этом случае, как нетрудно убедиться, всегда больше нуля, т.е. с течением времени величина , а в этом случае, как нетрудно убедиться, всегда больше нуля, т.е. с течением времени величина 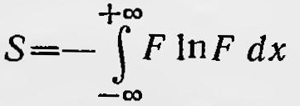 всегда возрастает. Пирогов математически не обосновывает утверждение, что при многократном процессе варьирования в пределе его ряд изменяется всегда в одном направлении, так что величина S обязательно возрастает. Правда, он не ограничивается простым утверждением этого положения, а приводит в его пользу некоторые соображения общего порядка. Однако эти соображения не являются сколько-нибудь строгими и имеют скорее чисто пояснительный характер. Тем не менее Пирогов применил здесь математический аппарат, который содержал в себе зачатки будущей теории стохастических процессов, для статистического обоснования второго закона термодинамики. всегда возрастает. Пирогов математически не обосновывает утверждение, что при многократном процессе варьирования в пределе его ряд изменяется всегда в одном направлении, так что величина S обязательно возрастает. Правда, он не ограничивается простым утверждением этого положения, а приводит в его пользу некоторые соображения общего порядка. Однако эти соображения не являются сколько-нибудь строгими и имеют скорее чисто пояснительный характер. Тем не менее Пирогов применил здесь математический аппарат, который содержал в себе зачатки будущей теории стохастических процессов, для статистического обоснования второго закона термодинамики.
Пусть теперь имеется макроскопическое тело, которое представляет систему из N материальных точек, состояние каждой из которых определяется шестью величинами: тремя слагающими скоростей (х, у, z) и тремя координатами (х, у, z). Таким образом, общее состояние всей системы может быть представлено как шестимерная последовательность R (x, у, z, х, у, z), которую вследствие огромного числа N можно рассматривать как «сплошную». Проводя затем для последовательности R рассуждения, аналогичные тем, которые имели место в случае одномерной последовательности А, можно образовать для нее тропометрическую величину и ее логарифм S: S = — ∫FInFdω, где F — функция распределения для последовательности R. С течением времени, в результате движения частиц рассматриваемой системы, функция распределения изменяется, а вместе с ней изменяется и S. В самом общем случае для любой системы из N частиц с любыми начальными условиями о характере изменения функции распределения и S никаких общих заключений сделать нельзя. Если, однако, предположить существование таких систем, частицы которых ведут себя с течением времени подобно членам рассмотренной выше одномерной последовательности, то для них справедливы все выводы, сделанные относительно поведения этой последовательности. Системы должны быть, очевидно, таковы, говоря словами Пирогова, что «изменение состояний частиц системы происходит «всячески»20. Эти слова означают требование, чтобы поведение каждой частицы было статистически независимым от поведения всех других частиц. Такие механические системы Пирогов называет «ненаправленными» системами. Применяя к ним рассуждения, аналогичные тем, которые проводились в случае одномерной последовательности при рассмотрении случайных изменений ее членов, получим, что изменение таких систем со временем всегда сопровождается возрастанием 5, так что δS/δt>0. Среди ненаправленных систем можно выделить такие, для которых значение координат и скоростей, принимаемых частицами, ограничено. Это консервативные системы, у которых изменение положения частиц в пространстве ограничено. Такие системы Пирогов называет «постоянными» системами. Для них величина S не может возрастать беспредельно, а должна стремиться к определенному наибольшему значению, допускаемому данными ограничениями. При этом система стремится к стационарному состоянию, т. е. к такому состоянию, при котором, несмотря на происходящие в системе движения, функция распределения и S остаются неизменными. Таким образом, условие стационарности ненаправленных постоянных систем таково: δS/δt = 0. Если предположить, что все макротела, состоящие из огромного числа микрочастиц, являются системами ненаправленными, то условие δS/δt≥0 и является молекулярно-кинетическим выражением второго закона термодинамики, а величина S должна быть просто связана с энтропией. Эту связь, а также связь S с другими макроскопическими термодинамическими величинами Пирогов устанавливает, рассматривая две системы, находящиеся в состоянии термодинамического равновесия, сначала — если они изолированы, а затем — при наличии между ними теплового контакта. В результате он получает, что S = η + а, где η — энтропия, а — некоторая постоянная. Возникает, естественно, вопрос, применимы ли выводы, относящиеся к ненаправленным системам, к реальному телу, рассматриваемому как система, состоящая из N частиц? Для того чтобы ответить на этот вопрос положительно, нужно предположить, что изменение состояния каждой частицы макротела происходит «всячески», т. е. совершенно случайным образом, и что поведение каждой частицы статистически независимо от поведения всех других. Но не противоречит ли это предположение законам механики, согласно которым, наоборот, изменение состояния всякой частицы самым строгим образом зависит от относительного положения и движения всех других частиц? Возможность разрешения этого противоречия Пирогов видит в чрезвычайной сложности движения частиц, составляющих макротело. Он высказывает предположение, что такая сложная система обладает только небольшим числом однозначных аналитических интегралов движения, а именно интегралом энергии и интегралом количества движения. Пирогов считает, что это позволяет обосновать статистическую независимость поведения частиц макротела. Работы Пирогова по статистическому обоснованию второго закона термодинамики не привлекли к себе внимания. При его жизни, как уже отмечалось, идея о чисто статистическом характере второго закона встретила скептическое отношение. В это время даже гораздо более известным работам Больцмана не было уделено должного внимания. В 90-е годы, когда начинается полемика вокруг H-теоремы Больцмана, Пирогова уже не было в живых и о его работах никто не вспомнил, тем более что идеи, положенные в их основу, не были достаточным образом подкреплены математическим аппаратом. 1Rаnkіnе W. Miscellaneous scientific papers, p. 428. 2Boltzmann L. Wissenschaftliche Abhandlungen. В. I. Leipzig, 1909, S. 9. 3Boltzmann L. Wissenschaftlichen Abhandlungen. В. I, S. 30—31. 4С1ausius R. Ann. Phys. B. 142, 1871, S. 435. 5Tам жe, S. 461. 6Можно было бы вычислить полную вариацию интеграла действия, т. е варьировать также и время. Однако мы ограничились более простым случаем варьирования, так как ничего нового такое более полное рассмотрение не дает. 7Boltzmann L. Wissenschaftliche. Abhandlungen. В. I, S. 295. 8Михельсон В. А. Собр. соч. Т. I. М., 1930, с. 66. 9Boltzmann L. Wissenschaftliche. Abhandlungen. В. I, S, 316—317. 10Boltzmann L. Wissenschaftliche Abhandlungen. В. I, S. 345—346. 11Loschmidt J. Sitzungsber, Acad. Wiss., Wien. В. 73, 1876. S. 128, 12Boltzmann L. Wissenschaftliche Abhandlungen. В. II, S. 121. 13Больцман называет величину Z распределяемостью (permutabilität). 14Эта приближенная формула является, как известно, формулой Стирлинга. 15Больцман Л. Очерки методологии физики. М., 1929, с. 47. 16Helmholtz H. Wissenschaftliche Abhandlungen. В. III. Leipzig, 1895, S. 176. 17Столетов А. Г. Собр. соч. Т. II, с. 317—318. 18Подробно о работах H. Н. Пирогова см. статьи Б. И. Спасского и В.П.Гончарова в сб.: История и методология естественных наук, вып. 1, физика. Изд-во МГУ, I960. 19Пирогов H. Н.— ЖРФХО, т. 22, 1890, ч. физ., вып. 2., с. 44. 20Пирогов H. Н,— ЖРФХО, т. 22, с. 67. |
загрузка...
