§ 52. Развитие кинетической теории газов

Признав, что теплота есть движение, а не особого рода невесомое вещество, наука должна была выяснить и исследовать характер этого движения. Решение этой проблемы привело к возникновению и развитию кинетической теории газов, которая в дальнейшем превратилась в новую область физических наук — статистическую физику.

Физикам, занимавшимся исследованием характера теплового движения, естественно было бы начать с того, на чем остановились их предшественники, утверждавшие еще в XVII и XVIII вв., что теплота есть движение. Однако за время длительного господства вещественной теории теплоты их работы в значительной степени были забыты. С другой стороны, за этот период воззрения на внутреннее строение тел эволюционировали. Поэтому в середине XIX в., когда уже стало ясно, что теплота есть движение при построении конкретных теорий о характере этого движения пришлось все начинать почти с самого начала.

В вопросе о строении вещества в науке первой половины XIX в. существовало довольно сложное положение. Атомистические представления о строении вещества довольно широко использовались в науке XVII—XVIII вв. Эти представления использовал Ломоносов для объяснения как физических, так и химических явлений. Однако во второй половине XVIIIв. атомистическую гипотезу почти перестают использовать. Только в начале XIX в. благодаря работам английского химика Джона Дальтона (1766—1844) эта гипотеза стала использоваться. Первоначально Дальтон применил атомистическую гипотезу для объяснения закона парциальных давлений, открытого им в 1801 г. При этом он разработал теорию атомного строения вещества, которую затем использовал для объяснения химических процессов. Дальтон полагал, что атомы — это маленькие шарики, между которыми действуют силы притяжения и силы отталкивания. Силы отталкивания, по Дальтону, присущи, однако, не самим атомам вещества, а частицам теплорода, которые обволакивают их, обусловливая отталкивание между атомами. При нагревании тела количество теплорода в теле увеличивается; это приводит к тому, что силы отталкивания между атомами тела увеличиваются и они стремятся удалиться друг от друга. Этим, как считал Дальтон объясняется, в частности, и расширение тел при нагревании. Так как атомы различных веществ, по Дальтону, отличаются друг от друга величиной, следовательно, и весом, то перед ним встала задача определить относительный вес атомов различных элементов и их относительные размеры. Нужно было решить также, как соединяются атомы элементов, образуя химические соединения. Проделав большую работу, на основании различных соображений Дальтон составил таблицы атомных весов химических элементов (атомный вес водорода Дальтон принял за единицу) и дал первые формулы химических соединений, введя своеобразные обозначения для атомов химических элементов. Конечно, таблица атомных весов Дальтона была далека от совершенства, так же как и его химические формулы. Приняв для воды неправильную формулу НО, Дальтон неправильно определил и атомный вес кислорода, а отсюда и атомный вес углерода и других элементов. Список химических элементов Дальтона был невелик, кроме того, в него входили некоторые химические вещества, не являющиеся простыми. Однако общее учение Дальтона весьма прогрессивно. Оно стимулировало дальнейшее развитие химической науки и развитие атомистической гипотезы, которая после его работ стала гораздо более убедительной, чем прежде.

После опубликования основных работ Дальтона многие химики положили в основу своих исследований по химии атомистическую гипотезу и направили усилия на дальнейшее и более точное определение атомных весов и установление химических формул различных химических соединений. Однако вскоре они встретились с большими трудностями и противоречиями. Все началось с открытия Гей-Люссаком в в 1808 г. нового закона. Он установил, что газы соединяются всегда в кратных объемных отношениях. Так, например, один объем водорода соединяется с одним объемом хлора и при этом получается два объема хлороводорода (объемы измерялись при нормальных условиях) или два объема окиси углерода и один объем кислорода дают два объема углекислого газа. Этот весьма простой по форме закон было трудно объяснить согласно взглядам Дальтона. Если один объем хлора целиком реагирует с одним объемом водорода, то, полагая, что при этом один атом водорода соединяется с одним атомом хлора, легко было прийти к выводу, что одинаковые объемы хлора и водорода при одинаковых давлениях и температуре содержат одинаковое число атомов. Рассматривая другие реакции, это положение можно было обобщить и прийти к заключению, что вообще равные объемы всех газов при одинаковых условиях содержат одинаковое число частиц. Но, с другой стороны, один объем водорода и один объем хлора дают при реакции не один, а два объема хлороводорода. Значит, либо в единице объема хлороводорода содержится меньшее число частиц, либо при соединении хлора и водорода соединяются не целые атомы, а половинки. Второе предположение, казалось, противоречило основной гипотезе о существовании атомов, первое же несогласовывалось с казавшейся весьма правдоподобной гипотезой, объясняющей закон, открытый Гей Люссаком. Правильное решение вопроса дал итальянский ученый Авогадро. Он высказал гипотезу, которую выдвигал еще Ломоносов о необходимости различать два типа частиц: атомы и молекулы «элементы» [«корпускулы» (по терминологии Ломоносова)]. В 1811 г. Авогадро, введя понятие молекулы (интегральная молекула), дал правильное объяснение закону Гей-Люссака. Он предположил, что в равных объемах газов содержится не одинаковое число атомов, а одинаковое число молекул, и что частицы простых газов бывают сложными, их молекулы состоят из двух и более атомов. Независимо от Авогадро к той же гипотезе пришел в 1814 г. Ампер, который также предложил различать понятие атома и молекулы. Одако такая гипотеза входила в противоречие с электрохимической теорией Берцелиуса, согласно которой каждая частица простого элемента имеет положительный или отрицательный заряд. По этой теории, электрическая сила, которая действует между атомами, имеющими противоположный заряд, является причиной химических соединений элементов. Теория объясняла многие химические явления и была широко распространена. Но, по теории Берцелиуса, объединение в общую молекулу атомов одного и того же химического элемента необъяснимо, поэтому гипотеза Авогадро—Ампера ей противоречила.

Результаты продолжающихся экспериментальных исследований по определению атомных весов и химических формул веществ противоречили теории Берцелиуса. Целый ряд соединений, особенно органических, никак нельзя было объяснить тем, что атомы одних элементов всегда электроположительны, а других — электроотрицательны. Против теории Берцелиуса возникла серьезная оппозиция и развернулась дискуссия. Берцелиусу и его приверженцам для «спасения» теории пришлось прибегнуть к ряду дополнительных гипотез, касающихся также и вопросов атомного строения вещества. В результате к 40-м годам прошлого столетия в химии возникла путаница: для одного и того же химического вещества существовало несколько формул, разные ученые предлагали разные значения атомных весов и т. д. Такая ситуация вызвала у некоторых ученых стремление ограничиться лишь установлением несомненных эксприментальных закономерностей нежелание строить какие-либо гипотезы о строении вещества. Они стали даже отрицать реальное существование атомов. Так, например, известный французский химик Дюма высказался за изъятие понятия об атоме и утверждал, что атомная теория — это пройденный этап в развитии химии. Уэвелль в «Истории индуктивных наук» писал:

«... мнение о том, что материя состоит из атомов, которое привело его к этим законам (речь идет о Дальтоне Б. С.) и посредством которого он выразил свой взгляд на их причины, не так важно и не так достоверно. Приписывая этому открытию большое значение, как одному из важнейших событий в истории химии, я разумею под этим открытием только закон явлений, т. е. те правила, которыми определяются количества составных частей, входящих в состав сложных тел»¹.

Таким образом, к середине XIX в. атомистика, которая с таким успехом была применена в начале века Дальтоном, стала рассматриваться многими химиками как пройденный этап. Среди физиков атомистическая гипотеза также не могла получить серьезной поддержки. Несмотря на то что многие физики не возражали против нее, роль этой гипотезы в развитии физической науки пока еще была очень и очень ограничена. Развитие физических наук не достигло еще такого уровня, когда наблюдаемые закономерности можно непосредственно связать с теми или иными атомно-молекулярными гипотезами, и эта гипотеза еще не стала необходимой при разработке конкретных физических теорий. В 1844 г. Герцен, критикуя агностицизм современных ему химиков, писал:

«... лет двадцать тому назад атомы составляли основание всех химических исследований Теперь же, принимая их, вас предупреждают обыкновенно на первой странице, что естествоиспытателям, собственно, дела нет, в самом ли деле тела состоят из крупинок чрезвычайно неделимых, невидимых, но имеющих свойства, объем и вес, или нет,— что их принимают так, для удобства. Таким ленивым приниманием они сами уронили свою теорию; они виноваты в том, что прошедшая философия нападала на атомизм со злым ожесточением; она рассматривала его в том бедном виде, в котором атомизм излагался во введениях к курсам физики и химии»².

Помимо этого, недоверчивое отношение к атомистической гипотезе было связано у физиков со скептическим отношением к натурфилософии вообще.

«... В среде физиков,— пишет Розенбергер,— постепенно распространилось пренебрежение или даже ненависть к натурфилософии вообще, и вскоре они пришли к такой точке зрения, в силу которой в учении о материи все казалось запрещенным, а потому самому и дозволенным. О строении материи и свойствах ее сил по меньшей мере избегали говорить, и только в сочинениях некоторых выдающихся физиков-математиков можно отыскать достаточный материал для того, чтобы воспроизвести господствовавшее в то время учение о материи»³.

Правда, физики, иногда использовали представление об атомистическом строении материи. Так, например, представлением о дискретном строении вещества и даже эфира пользовались Френель и другие

«... все исследование следует признать основным на чисто гипотетических принципах, из которых выводятся математические представления о явлениях упругой среды... Первоначальные принципы сами по себе включают предположения, которые представляются очень сомнительными и не являются удовлетворительной основой для математической теории, а именно что упругость среды определяется вертикальным движением ее молекул и последовательными ударами об упругую тяжелую плоскость»⁴.

Приведя эти рецензии, Релей заключает:

«... история этой работы наводит на мысль, что чисто спекулятивные исследования, особенно неизвестного автора, лучше всего преподносить миру через другие каналы, чем научное общество, которое, естественно, колеблется допустить в свой печатный орган работу сомнительной ценности»⁵.

Однако дело не только в этом. Работа Ватерстона противоречила и установившимся физическим представлениям, и укоренившимся методологическим принципам. Ведь тогда еще считалось общепризнанным, что теплота есть «невесомая материя»; с другой стороны, еще были сильны традиции ньютонианской физики, запрещающей «измышление гипотез».

Начиная с 50-х годов в печати появляются работы, посвященные исследованию тепловых явлений с точки зрения представления о молекулярном движении. Так, уже в 1850 г. Ранкин⁶ пытается рассмотреть теплоту как особый род невидимых скрытых движений, протекающих в атомно-молекулярной области. Интересно, что при этом он возрождает в новой форме идею Ломоносова о тепловом движении как вращательном (коловратном). Ранкин полагает, что атом состоит из ядра и упругой атмосферы, удерживающейся силами притяжения около ядра. Вращение и колебание этих атмосфер и есть тепловое движение. Основываясь на таких представлениях о природе теплоты, Ранкин и пришел к ряду выводов, относящихся к термодинамике.

В 1851 г. Джоуль опубликовал работу «Некоторые замечания о теплоте и о строении упругих жидкостей»⁷. Первоначально Джоуль рассматривал теплоту как вращательное движение электрических атмосфер, окружающих атомы, но затем отказался от этой мысли. В данной статье он рассматривает вопрос о тепловом движении частиц газа и полагает, что тепловым движением является их поступательное движение. Эта гипотеза представлялась Джоулю проще и правдоподобнее гипотезы о теплоте как вращательном движении частиц газа, хотя последняя, как он считает, в равной мере согласуется с наблюдаемыми явлениями.

Первая работа по кинетической теории газов, в которой содержались новые существенные результаты, была опубликована в 1856 г. и принадлежала немецкому ученому Крёнигу⁸. Крёниг рассматриваученые, занимающиеся исследованием распространения волн в упругой среде. Немецкий ученый Фехнер специально даже подчеркивал:

«Волновая теория есть необходимый момент физики, атомистика есть необходимый момент волновой теории; следовательно, атомистика есть необходимый момент естествознания»⁹.

Изменение отношения к атомистической гипотезе строения вещества начинает намечаться в середине XIX в., и основным толчком к этому послужило открытие эквивалентности теплоты и работы и закона сохранения и превращения энергии. Начиная с середины XIX в. появляются работы, в которых авторы пытались объяснить газовые законы и тепловые явления. Англичанин Ватерстон в 1845 г. представил в редакцию трудов Королевского общества для опубликования статью под названием «0 физической среде, состоящей из свободных и вполне упругих молекул, находящихся в движении». Однако эта статья увидела свет гораздо позже, в 1892 г.¹⁰. Ватерстон считал, что тела состоят из молекул — упругих шариков, движение которых и есть теплота. В твердых телах это колебательное движение около положений равновесия. В газах же молекулы выходят из сферы действия молекулярных сил и движутся как свободные материальные тела, т. е. поступательно. Ударяясь о стенки и отскакивая от них, молекулы создают в результате этого непрерывно действующую силу — давление на стенки. Для количественных расчетов Ватерстон рассматривает тяжелую горизонтальную плиту, о которую непрерывно ударяется множество шариков и тем самым поддерживает ее, не давая упасть. С помощью такой простой модели, используя элементарные подсчеты, Ватерстон приходит к выводу, что упругость газа пропорциональна плотности и живой силе его молекул. Отсюда следуют законы Бойля—Мариотта и Гей-Люссака, если полагать, что абсолютная температура газа пропорциональна средней кинетической энергии ' («живой силе») его молекул. Ватерстон затронул ряд других вопросов кинетической теории: теплоемкости газов, распределения температуры газа в поле тяжести в зависимости от высоты и др. В некоторых случаях, несмотря на упрощенные представления о тепловом движении, Ватерстон сделал правильные выводы. Так, например, он получил (хотя и неправильным путем), что в газе, состоящем из смеси различных молекул, «средний квадрат молекулярной скорости обратно пропорционален удельному весу молекул»¹¹.(Спустя 15 лет эти же данные получил Максвелл.) В предисловии к работе Ватерстона Релей обсуждает вопрос, почему она не была напечатана в свое время, ссылаясь при этом на рецензии,которые он нашел вместе со статьей в архивах общества. Один рецензент утверждает, что работа пустая, если не бессмысленная, негодна даже для чтения перед обществом¹². В другой рецензии, более сдержанной, отмечается: газ как совокупность мельчайших упругих шариков-атомов, движущихся хаотично в пустом пространстве. Ударяясь о стенки сосуда, эти шарики создают постоянную силу — давление газа. Для того чтобы подвергнуть количественному анализу движение частиц газа, Крёниг использует идею хаотичности их движения. Он пишет:

«По отношению атомов газа гладкая стенка должна рассматриваться как очень неровная и поэтому траектория каждого атома настолько беспорядочна, что не поддается никакому расчету. Однако, по законам теории вероятности, вместо этой полной беспорядочности можно принять полную упорядоченность»¹³.

Это очень интересное заключение. Оно является одним из первых предположений о возможности и необходимости применения теории вероятности для исследования физических явлений. Исходя из этих соображений, Крёниг полагает возможным принять, что атомы газа движутся по трем взаимно перпендикулярным направлениям с одинаковой скоростью. Следовательно, если газ находится в сосуде, имеющем форму прямого параллелепипеда, то можно считать, что направления движения частиц параллельны трем его взаимно перпендикулярным ребрам. Сделав такое предположение и проведя элементарный расчет, Крёниг выводит уравнение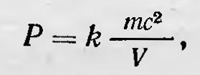

где Р — давление газа, V — его объем, m — масса, с — скорость атомов. (Коэффициент пропорциональности k, по Крёнигу равен одной шестой числа всех атомов газа. В действительности он равен не 1/6, а 1/3 числа молекул.)

Сравнивая полученное уравнение с уравнением газового состояния, Крёниг устанавливает, что живая сила атомов «есть не что иное, как отсчитанная от абсолютного нуля температура». Из теории Крёнига следует также, что «газы при равном давлении и равной температуре содержат в равном объеме равное число атомов», т. е. закон Авогадро. Теория Крёнига объясняет ряд свойств газа, в частности охлаждение его при адиабатическом расширении и т. д. Появление работы Крёнига в печати заставило Клаузиуса в следующем году опубликовать свои исследования по кинетической теории газов, которые он, по его словам, начал вести еще до того, как опубликовал свою первую работу по термодинамике.

«Еще до того, как я опубликовал в 1850 г. исследование о теплоте, в котором предполагается, что теплота есть движение, я уже образовал для себя представление о природе этого движения, которое я также уже применял к различным исследованиям и расчетам,— пишет Клаузиус и продолжает, —я умышленно не упоминал об этом представлении в моих исследованиях, потому что хотел отделить заключения, которые я вывел из некоего общего принципа, от таких, которые предполагают определенный вид движения»¹⁴.

В этой работе Клаузиус разработал более совершенную кинетическую модель идеального газа, чем модель Крёнига. Клаузиус рассматривает теплоту как движение атомов и молекул. В твердом теле молекулы совершают движение вокруг определенных положений равновесия, а в жидкости молекулы могут двигаться и поступательно, но так, что они не разлетаются во все стороны, а остаются в пределах определенного объема. В газах же молекулы выходят из сферы взаимного притяжения и движутся поступательно во все стороны, сталкиваясь между собой. Однако кроме поступательного движения молекулы газа участвуют и во вращательных движениях, а также могут обладать внутренними движениями — движением частей молекул. Для вывода количественных закономерностей Клаузиус рассматривает идеальный газ, заключенный в сосуд, имеющий форму параллелепипеда, в котором молекулы газа пролетают от одной стенки до другой, от одного основания до другого, не сталкиваясь между собой. При этом все молекулы движутся с одной и той же средней по величине скоростью, но в разных направлениях, причем все направления движения молекул одинаково часто встречаются. Для обоснования этих предположений Клаузиус ссылается на теорию вероятностей. Приняв, наконец, что столкновения молекул со стенкой происходят по законам упругого удара, он делает вывод, что давление, оказываемое на стенку сосуда, равно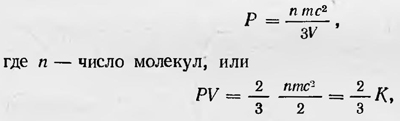

где К — энергия поступательного движения молекул. Принимая, наконец, что Р п V связаны уравнением Клапейрона, он окончательно получает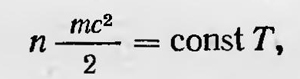

т. е. что «живая сила поступательного движения газовых молекул» пропорциональна абсолютной температуре.

В дальнейшем Клаузиус дал более строгий вывод этого уравнения, используя менее упрощенное представление о движении молекул газа. В данной работе Клаузиус коснулся также ряда других вопросов кинетической теории газов. С точки зрения этой теории он объясняет явления кипения и конденсации газов и т. д. Клаузиус также указывает на возможность подсчета скорости газовых молекул какого-либо газа при данной температуре и сам производит такой расчет. Так, например, для молекул кислорода он получил, что средняя скорость их при 0°С равна примерно 450 м/с. Работа Клаузиуса обратила на себя внимание и даже вызвала возражения. Так, голландский ученый Бейс-Баллот, высказавший еще в 1849 г. мнение о том, что теплота есть колебательное движение частиц тела (включая и газ), возражал Клаузиусу. Свои возражения он аргументировал тем, что, по теории Клаузиуса, получаются весьма большие средние скорости молекул газа, что противоречит, по его мнению, явлению диффузии. Известно, что облако табачного дыма в комнате может долгое время не расходиться; углекислый газ долго удерживается в открытом сосуде и т. д.

Джемс Клерк Максвелл

Такого рода возражения были обусловлены тем, что Клаузиус в своей работе обошел вопрос столкновения молекул газа друг с другом. Клаузиус разъяснил ошибочность подобного рода возражений в последующей работе, в которой он ввел понятие средней длины свободного пробега молекул газа. Первоначально он исходил из простой модели. Он рассматривал газ состоящим из неподвижных молекул, распределенных с равномерной плотностью по объему, среди которых с постоянной средней скоростью движется одна молекула. Исходя из таких простых предположений, Клаузиус получил для средней длины свободного пробега формулу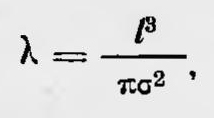

где l — среднее расстояние между соседними молекулами; σ — сфера действия молекулы, которая равна ее диаметру, если молекулы считать за шарики. (В последующем он несколько усложнил модель и получил, что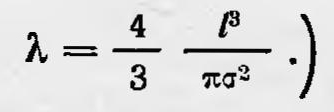

Новым важным шагом в развитии кинетической теории газов явилась работа Джемса Клерка Максвелла (1831—1879) «Пояснение к динамической теории газов» (1860), в которой он впервые вывел закон распределения скоростей газовых молекул. Этой работе предшествовало исследование Максвелла, посвященное строению колец Сатурна. Максвелл показал, что эти кольца должны состоять из множества мелких твердых частиц, самостоятельно вращающихся вокруг Сатурна со скоростями, зависящими от их расстояния до планеты. Весьма возможно, как указывают биографы Максвелла Кемпбелл и Гарнетт, что представление о кольцах Сатурна как о скоплении мелких частиц, движущихся самостоятельно с различными скоростями, привело Максвелла к исследованию вопросов, относящихся к кинетической теории газов1¹⁵. Во всяком случае, последующая работа Максвелла была посвящена кинетической теории газов. Максвелл довольно осторожно определяет ее задачи. Он указывает, что исследует

«... законы движения неопределенного количества малых твердых и совершенно упругих шаров, действующих друг на друга только во время столкновения. Если окажется, что свойства подобной системы тел соответствуют свойствам, газов, то этим будет создана важная физическая аналогия, которая может привести к более правильному познанию свойств материи»¹⁶.

Максвелл говорит не просто о теории строения газов, а о модели газа, которая приблизительно соответствует реальности. Эта идея о роли аналогии, используемая при построении физической теории, является одной из основных идей, которыми пользуется Максвелл в своем научном творчестве. Этот метод построения физической теории особенно четко проявился у Максвелла при построении теории электромагнитного поля. Используя указанную модель, Максвелл выводит закон распределения скоростей молекул газа (закон распределения скоростей Максвелла). Этот вывод хорошо известен. В основе его лежит предположение о статистической независимости компонент скоростей, молекул газа. Если среднее число упругих шаров (т. е. молекул), имеющих слагающие скорости вдоль оси х в пределах v_x и v_x + dv_x, равно Nf(v_x)dv_x, а соответственно среднее число частиц, слагающие скорости которых по осям у и z лежат в пределах v_у, v_у + dv_у и v_z, v_z+ dv_z, равно Nf(v_у)dv_у и Nf(v_у)dv_z, то среднее число частиц, слагающие скорости которых одновременно находятся в пределах v_x; v_x + dv_x; v_у,v_у + dv_у; v_z ,v_z + dv_z, если использовать указанное выше предположение, таково:

Nf(v_x)f(v_уf(v_z)dv_xdv_уdv_z,

где N — общее число частиц.

С другой стороны, так как все направления скоростей «совершенна произвольны», данное число частиц должно зависеть только от их абсолютной скорости; это условие приводит к функциональному уравнению

f(v_x)f(v_уf(v_z)=φ(v²_x+v²_y+v²_z).

Решая это уравнение, Максвелл и приходит к известному выражению закона распределения скоростей молекул газа. Этот вывод закона распределения скоростей молекул газа подвергался критике. Указывалось, что основное предположение Максвелла о статистической независимости компонент скоростей молекул газа далеко не очевидно. Однако вскоре Максвелл привел более строгое доказательство закона распределения скоростей молекул газа. Впоследствии были предложены и другие способы доказательств этого закона и, наконец, было показано, что этот закон вытекает из общих положений статистической физики.

В этой же работе Максвелл останавливается и на других вопросах кинетической теории газов. Он рассматривает вопрос о длине свободного пробега молекул газа и вычисляет ее, исходя из предположения, что скорости молекул не равны некоторой средней скорости, а распределены по выведенному им закону. Максвелл получает более точное выражение для средней длины свободного пробега, чем Клаузиус: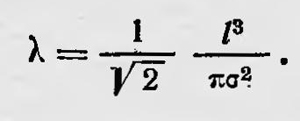

Затем Максвелл останавливается на вопросе о внутреннем трении и диффузии газов. Для коэффициента внутреннего трения Максвелл получил выражение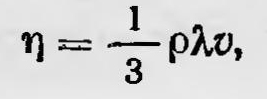

где ρ — плотность газа, a v — средняя скорость молекул газа. Отсюда следует интересный вывод. Если подставить в выражение для ц значение длины свободного пробега, то получим, что коэффициент внутреннего трения не зависит от давления газа. Этот вывод был для Максвелла настолько неожиданным, что показался ему подозрительным. В дальнейшем он был проверен экспериментально и получил подтверждение.

Максвелл дает первый набросок кинетической теории теплопроводности и диффузии газов и в заключение останавливается на вопросе о молекулярном толковании теплоемкостей газов. Он рассматривает молекулы газа не только как упругие гладкие шарики, но как упругие тельца несферической формы, при соударении которых уже надо учитывать возможность вращения их вокруг центра тяжести. Применяя законы удара, а также некоторые теоретико-вероятностные соображения, путем еще недостаточно строгих рассуждений Максвелл приходит к выводу, что «средняя живая сила перемещения вдоль каждой из трех осей во всех системах одинакова и равна средней живой силе вращения около каждой из трех главных осей каждой частицы»¹⁷, т. е. к выводу о равномерном распределении средней энергии по степеням свободы. В дальнейшем Максвелл на основе более строгой теории получил тот же самый результат.

В 1866 г. в работе «Динамическая теория газов»¹⁸ Максвелл привел более строгое доказательство закона распределения скоростей молекул газа. Пусть имеется смесь двух сортов газов, массы молекул которых соответственно равны m₁ и m₂. Пусть, далее, f₁ и f₂ — функции распределения скоростей молекул газов первого и второго сорта. Запишем число соударений n₁ молекул одного сорта с молекулами второго сорта в единицу времени для случая, когда соударяющиеся молекулы первого сорта имели до удара скорости в интервале с₁, c₁ + dc, а молекулы второго сорта в интервале с₂, с₂ + dc, а после удара их скорости лежат соответственно в интервалах с₁', c₁' + dc и с₂' , с₂' + dc:

n₁=f₁(c₁)dcf₂(c₂)dcΦ,

где Φ — некоторая функция, зависящая от относительной скорости сталкивающихся молекул, от углов, определяющих направление их скоростей до удара и после, и т. д. Определим теперь число n₂ обратных еоударений в единицу времени,т. е. таких, в результате которых молекулы первого газа, имеющие скорости с₁', c₁' + dc, и молекулы второго, скорость которых с₂', с₂' + dc, приобретут соответственно скорости с₁, с₁ + dc и с₂, с₂ + dc.

n₂=f₁(c₁')dcf₂(c₂')dcΦ'.

В случае стационарного состояния n₁=n₂; кроме того, по расчетам Максвелла,

Φ(dcf)²= Φ'(dc)².

Таким образом, для случая стационарного состояния или статистического равновесия Максвелл получает функциональное уравнение

f₁(c₁)f₂(c₂)=f₁(c₁')f₂(c₂'),

решая которое с учетом, что при соударении справедлива теорема живых сил, он приходит к известному уже закону распределения скорости молекул газа.

В дальнейшем (вплоть до начала нашего столетия) наиболее важные результаты в развитии кинетической теории газа и кинетической теории теплоты вообще были получены австрийским физиком Людвигом Больцманом (1844—1906). Уже в 1866 г. Больцман приводит усовершенствованный вариант доказательства закона распределения скоростей молекул газа, исходя, подобно Максвеллу, из рассмотрения соударения молекул, а затем совершенствует его. При этом он рассмотрел и более общий случай идеального газа, находящегося в силовом поле, обобщил на этот случай закон распределения и вывел так называемый закон распределения Максвелла — Больцмана, согласно которому функция распределения для молекул газа выражается формулой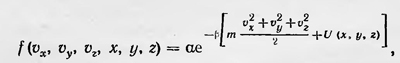

где α и β — коэффициенты, зависящие от температуры, U(x, у, z) — потенциальная энергия молекул газа.

В процессе таких исследований Больцман вывел кинетическое уравнение для идеального газа (1872) и впервые доказал знаменитую Н-теорему (это название было дано позже), согласно которой идеальный газ, находящийся первоначально в нестационарном состоянии, сам собой с течением времени должен переходить в состояние статистического равновесия, а функция распределения при этом становится функцией распределения Максвелла — Больцмана. Это доказательство Больцман истолковал как доказательство статистического характера второго закона термодинамики о теореме и о статистическом толковании второго закона термодинамики будет сказано ниже).

Новый шаг в развитии кинетической теории газов был сделан голландским физиком Ван-дер-Ваальсом. Он разработал в 1873 г. первую теорию реальных газов, в которой учитывались размер молекул и силы, действующие между ними. Воспользовавшись теоремой вириала и применяя ряд простейших предположений о межмолекулярных силах и тепловом движении молекул газа, Ван-дер-Ваальс получил уравнение состояния газов, описывающее качественно также и жидкое состояние.

Людвиг Больцман

Теория Ван-дер-Ваальса сыграла определенную роль в обосновании кинетической теории газов вообще. Кинетическая теория газов хотя и объяснила уже многие явления и свойства газов, но предсказала пока только одно свойство газов — независимость внутреннего трения от плотности газов. Теория Ван-дер-Ваальса дала возможность предсказать новые явления, а также получить новым способом количественные характеристики молекул газов.

Еще до Ван-дер-Ваальса были сделаны первые попытки определения размеров молекул, их числа в единице объема и т. д. Австрийский физик И. Лошмидт уже в 1865 г. напечатал работу, посвященную определению размеров молекул¹⁹. Он исходил из следующих соображений. По теории Клаузиуса следовало, что средняя длина свободного пробега молекул газа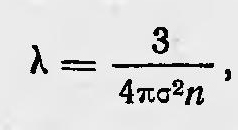

где δ — диаметр молекулы, n — число молекул в единице объема. Запишем эту формулу в ином виде:

l = 4/3πδ²nλ

и умножим обе части равенства на δ:

δ = 4/3πδ³nλ.

Тогда, учитывая, что объем каждой молекулы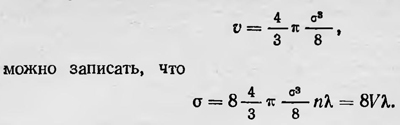

Величина vn = V равна объему всех молекул в единице объема газа. Эту величину Лошмидт назвал множителем уплотнения. Теперь, полагая, что в жидкости молекулы соприкасаются друг с другом, можно определить отношение удельной плотности вещества в газообразном и жидком состоянии. Если в газообразном состоянии вещество занимает объем, равный единице, то в жидком состоянии оно должно занимать объем, равный 6V/π, и отношение плотности вещества в жидком состоянии ρ_ж к плотности в газообразном состоянии ρ_г таково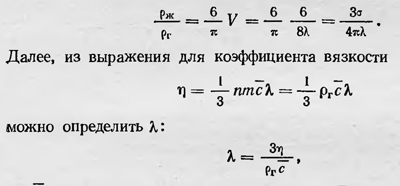

где с — средняя скорость газовых молекул. Подставляя теперь значение λ в выражение для отношения плотностей, получаем

Так как с можно выразить через температуру из закона Максвелла или из соотношения Клазиуса ρV = 1/3nmc², то можно определить о, измерив коэффициент вязкости газа и зная его плотность, а также плотность жидкости. Такой подсчет и произвел Лошмидт для воздуха²⁰, получив значение σ = 12*10_-8 см; в скором времени был определен диаметр молекул и других веществ (значение их оказалось того же порядка величины).

Теория Ван-дер-Ваальса также давала возможность определить размеры молекул совершенно другим путем. В уравнении

(p+a/V²)(V-b)=pT величина b просто связана с величиной объема всех молекул. Таким образом, определяя Ь, можно вычислить диаметр молекул. Результаты таких расчетов не сильно отличались от результатов, полученных Лошмидтом, что явилось одним из первых существенных подтверждений основных идей кинетической теории газов.

Помимо указанных методов в начале 80-х годов был предложен новый метод определения размеров молекул — с помощью измерения диэлектрических постоянных газов. Используя теорию электрической поляризации, Дорн в 1881 г. определил размеры молекул некоторых газов и получил результаты, близкие к результатам Лсшмидта и Ван-дер-Ваальса. Одновременно с определением размеров молекул было найдено число молекул в единице объема газа при нормальных условиях, названное числом Лошмидта, а также число молекул в одной грамм-молекуле — число Авогадро. Теперь кинетическая теория газов получила солидное обоснование. Она объяснила многие свойства газов, предсказала некоторые новые явления и стала новым разделом физических наук. Однако перед ней стояла еще одна важнейшая проблема — проблема молекулярного обоснования второго начала термодинамики.

¹Уэвелль В. История индуктивных наук. Т. III. СПб., 1869, с. 205.
²Герцен А. И Избранные философские произведения. Т. I. М., Госполитиздат, 1948, с. 107.
³Розенбергер Ф. История физики. Ч. Ill, вып. 1. М.—Л., 1935, с 62.
⁴Waterston Y. Philos. Trans. (A). Vol. 183, п. 2—3.
⁵Там же, p. 3.
⁶Rankine W. Miscellaneaus scientific papers. London. 1881, p. 16.
⁷Джоуль Дж. П. Некоторые замечания о теплоте и о строении упругих жидкостей. В кн.: Основатели кинетической теории материи. М.-Л., ОНТИ, 1937 с 31
⁸Kronig A., Ann. Phys. В. 99, 1856, S. 315.
⁹Fechner Q. Ober die physikalische und philosophische Atomenlehre. Zeipzig, 1864, S. 24.
¹⁰Waterstоn J. Phil. Trans. (A). Vol. 163, 1892, p. 1
¹¹Там же, p. 16.
¹²Там же, p. 2.
¹³Kronig A. Ann. Phys. В. 99, S. 318.
¹⁴Clausius R. Ann. Phys. B. 100, 1857, S. 353.
¹⁵D Campbell L., Garnett W. The life of James Clerk Maxwell. London, 1882, p. 562.
¹⁶Максвелл Дж. К. Пояснение к динамической теории газов.— 13-кн.: Основатели кинетической теории материи, с. 187.
¹⁷Максвелл Дж. К- Пояснения к динамической теории газов.— В кн.: Основатели кинетической теории материи, с. 219.
¹⁸Махwell J. С. The scientific papers. Vol. II, Cambridge, 1890, p. 26.
¹⁹Loschraidt J. Sitzungsber. Acad. Wiss., Wien. В. 52, 1866, S. 395
²⁰Заметим, что Лошмидт не мог, конечно, определить плотность жидкого воздуха, так как в то время еще не был найден способ его сжижения, поэтому ему пришлось определять эту величину, исходя из некоторых дополнительных соображений.

<<Назад Вперёд>>

Просмотров: 4813

загрузка...

Другие книги по данной тематике