§ 51. Установление основ термодинамики
|
К середине XIX в. паровая машина получает все большее и большее распространение в промышленности. Вместе с этим все большее и большее значение начинает приобретать и теория самой машины. Это стимулирует исследования по термодинамике. С другой стороны, открытие механического эквивалента теплоты дает новые основы для ее развития по сравнению с теми основами, на которых строил теорию этой машины Карно.
В 1849 г. Вильям Томсон, получивший впоследствии титул лорда Кельвина (1824—1907), занялся расчетами мощности теплового двигателя, взяв за основу теорию Карно и используя новые данные по измерению тепловых величин газов и паров, полученных французским ученым Реньо. Томсон еще опирается на гипотезу о теплороде, хотя знает о работах Джоуля. Однако он все же решает придерживаться прежних взглядов. Но уже в следующем, 1850 г. Рудольф Клаузиус (1822—1888) подходит к вопросу о работе паровой машины и вообще к вопросу о совершении теплотой работы с новой точки зрения. Вопреки мнению Карно Клаузиус считает, что не все количество теплоты, взятое у нагревателя, передается холодильнику. Часть его превращается в совершаемую машиной работу. Вообще, когда телу сообщается некоторое количество теплоты dQ, то в общем случае часть этого количества идет на нагревание этого тела, а другая часть превращается в работу, которую совершает тело, расширяющееся при нагревании. При этом между количеством теплоты и работой существует постоянное соотношение — механический эквивалент теплоты или тепловой эквивалент работы. Это общее положение Клаузиус рассматривает как первое основное положение механической теории теплоты. Для случая идеального газа оно имеет вид 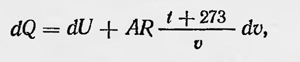
где R — постоянная для данного газа, А — тепловой эквивалент работы; второй член правой части равенства выражает величину работы, a dU — приращение некоторой функции состояния, определяемое в данном случае приращением температуры (впоследствии ее стали называть внутренней энергией). При работе тепловой машины часть количества теплоты, взятая у нагревателя, превращается в работу, а часть его передается холодильнику. Это обязательное условие ее работы. Таким образом, Карно в каком-то отношении прав, рассматривая процесс работы тепловой машины как результат перехода теплоты от нагревателя к холодильнику. Такой процесс совершается, но не для всего количества тепла, взятого у нагревателя. 
Вильям Томсон (Кельвин) «Переход теплоты от теплого тела к холодному,— пишет Клаузиус, — всегда имеет место, когда теплота совершает работу и одновременно выполняется условие, что рабочее вещество в заключение приходит в то же самое состояние, в каком оно было вначале»1. 
Рудольф Клаузиус В связи с этим можно утверждать, указывает Клаузиус, что теплота «всегда обнаруживает тенденцию к уравниванию температурной разницы путем перехода от тепловых тел к холодным»2. Это положение является вторым основным положением «механической теории» теплоты. Применение этого положения позволяет доказать теорему Карно. Для этого нужно также рассмотреть две тепловые идеальные машины с различными рабочими веществами, работающие при одних и тех же нагревателях и холодильниках, но в противоположных направлениях. Если одна из этих машин, забирая теплоту у нагревателя совершает работу и часть этой теплоты передает холодильнику, то другая, наоборот, возвращает забранную теплоту нагревателю и над ней совершается работа. Если обе машины аналогичны машине Карно, т. е. совершают замкнутые обратимые циклы, то, применяя второе основное положение, легко получить, что коэффициент полезного действия машин должен быть одинаков или что коэффициент полезного действия не зависит от рабочего вещества, а зависит только от температур нагревателя и холодильника. Таким образом, доказана та же самая теорема, справедливость которой показал Карно, исходя из неправильных представлений о природе теплоты. В этой же работе Клаузиус впервые определяет выражение для функции Карно С, которая просто равна обратной величине абсолютной температуры. Вслед за первой работой Клаузиуса по термодинамике последовал начиная с 1851 г. ряд работ Томсона под общим заглавием «О динамической теории теплоты». В них Томсон впервые исходил из новых представлений о природе теплоты, основывался на двух основных положениях: эквивалентности теплоты и работы и теореме Карно. Первое основное положение является выражением общего «принципа механической работы», т. е. закона сохранения и превращения энергии, второе же устанавливается на основе следующей аксиомы, которую постулирует Томсон: «Невозможно при помощи неодушевленного материального деятеля получить от какой-либо массы вещества механическую работу путем охлаждения ее ниже температуры самого холодного из окружающих предметов»3. Используя эту аксиому, являющуюся одной из первых формулировок второго начала термодинамики, Томсон, подобно Клаузиусу, доказывает теорему Карно. При этом Томсон отмечает, что приоритет доказательства принадлежит Клаузиусу, но что он пришел к этому доказательству и к установлению аксиомы, которая отличается от второго положения Клаузиуса только по форме, самостоятельно. Далее он определяет выражения функции Карно и коэффициента полезного действия машин Карно. В современных обозначениях этот коэффициент имеет вид 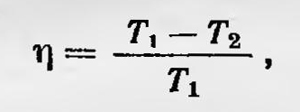
где Т1 и Т2 — соответственно температура нагревателя и холодильника. В этих же работах Томсон возвращается к вопросу об абсолютной шкале температур, который он уже исследовал ранее, исходя из теории Карно и его взглядов на природу теплоты. Он устанавливает абсолютную температурную шкалу: «Температуры двух тел пропорциональны количествам теплот, соответственно взятой и отданной материальной системой в двух местах, имеющих эти самые температуры, когда система совершает полный цикл идеальных обратимых термодинамических процессов и защищена от потери или прибавления теплоты при какой-либо другой температуре»4. В одной из статей, относящейся к 1854 г., Томсон идет дальше и дает новое математическое выражение для второго начала термодинамики. Если система совершает сложный обратимый цикл и получает или отдает при этом количества теплоты Q1, Q2, Q3 ,... соответственно при температурах Т1, Т2, Т3,... (в современных обозначениях), то для всего цикла имеет место равенство 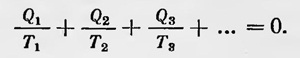
При этом количество теплоты, полученное системой, берется с положительным знаком, а отданное — с отрицательным. Томсон пишет, что это «уравнение может быть рассматриваемо как математическое выражение второго основного закона динамической теории теплоты»5. Тем временем Клаузиус также получает новые результаты в термодинамике. В работе, опубликованной в 1854 г., он дает расширенную формулировку первому «основному положению», которое математически записывается так: Q = U + AW, где AW — выраженная в тепловых единицах работа; в случае расширения тела она равна dW = pdV. Второй закон термодинамики Клаузиус теперь формулирует следующим образом: «Теплота не может переходить от более холодного тела к более нагретому, если одновременно не происходят в связи с этим другие изменения»6. (В дальнейшем Клаузиус продолжал уточнять формулировку второго начала термодинамики и окончательно остановился на следующей: «Переход теплоты от более холодного тела к более теплому не может иметь места без компенсации»7. В этой же работе Клаузиус приводит более общее математическое выражение второго начала термодинамики. Он рассматривает сложный круговой обратимый процесс, совершаемый рабочим телом, состоящим из изотерм и адиабат. При этом тело получает и отдает определенные количества теплоты dQ1 нагревателям и холодильникам при соответствующих температурах T1. Клаузиус получает тоже выражение, что и Томсон: 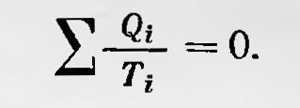
Обобщая затем этот вывод на случай любого обратимого кругового процесса, он приходит к выражению 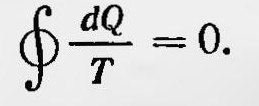
Помимо Томсона и Клаузиуса к некоторым основным понятиям термодинамики пришел Ранкин. Он уже в 1850 г. рассматривал работу тепловой машины так же, как и Клаузиус. Позже (одновременно с Клаузиусом) Ранкин делает вывод, что величина dQ/Т — полный дифференциал для обратимых процессов, и называет ее термодинамической функцией. Правда, вывод был далек от строгости и Ранкин неверно интерпретировал это понятие. Естественно, что основоположники термодинамики не могли остановиться на рассмотрении только обратимых процессов и не подвергнуть подробному физическому и математическому анализу реальные процессы, протекающие необратимо. Впервые этот вопрос затронул Томсон в работе «О проявляющейся в природе общей тенденции к рассеянию механической энергии» (1852); он получил весьма важные как в научном, так и в философском отношении результаты. Понимая под термином «механическая энергия» запас энергии, способной производить механическую работу, Томсон указал, что только системы тел, подверженные обратимым изменениям, обладают свойством восстанавливать «механическую энергию», т. е. восстанавливать способность производить ту же самую механическую работу. В случае же необратимых процессов, таких, как трение, теплопроводность и т. д., изолированная система тел не может прийти в первоначальное состояние, их «механическая энергия» непрерывно уменьшается и происходит «рассеяние механической энергии». Но так как все наблюдаемые явления происходят необратимо, то во всех изолированных материальных системах имеет место процесс «рассеяния механической энергии». Это положение Томсон распространяет на всю Вселенную, из него, по его мнению, следуют далеко идущие выводы: «В прошлом, отстоящем на конечный промежуток времени от настоящего момента, земля находилась и, спустя конечный промежуток времени, она снова очутится в состоянии, непригодном для обитания человека; если только в прошлом не были проведены и в будущем не будут предприняты такие меры, которые являются неосуществимыми при наличии законов, регулирующих известные процессы, протекающие ныне в материальном мире»8. Здесь впервые на основании второго закона термодинамики и распространения его на всю Вселенную, делается вывод о ее «тепловой смерти». Клаузиус выступил в печати по вопросу о необратимых процессах позже. Исследовав основные положения термодинамики обратимых процессов еще в 1854 г., он вплоть до 1862 г. не касался в печати вопросов необратимых процессов. Сам Клаузиус объяснял это так: «С публикацией другой части моего положения (речь идет о применении второго начала в необратимых процессах.— Б. С.), я медлил до сих пор, потому что она ведет к выводу, который сильно уклоняется от воззрений, распространенных до настоящего времени, и поэтому я хотел ее еще раз проверить»9. В работах 1862—1865 гг. Клаузиус специально останавливается на вопросе о необратимых процессах. Для таких процессов, полагает он, применение первого закона термодинамики ничего нового не дает. Использование же второго закона для необратимых процессов приводит к новому результату, а именно: 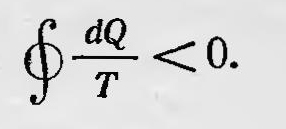
Таким образом, общее аналитическое выражение второго закона термодинамики и для обратимых и для необратимых процессов можно записать в виде 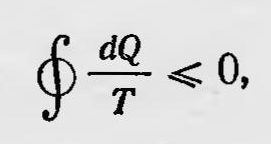
где знак равенства справедлив для обратимых, а знак неравенства — для необратимых процессов. Далее, так как для обратимых процессов данный интеграл по замкнутому контуру от dQ/Т равен нулю, то эта величина в нашем случае есть полный дифференциал. Следовательно, можно принять, что dQ/Т=dS, 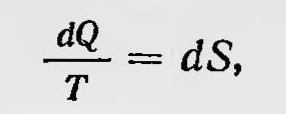
где S — некоторая функция состояния системы. Для необратимых же процессов справедливо неравенство dQ/Т Наконец, в общем случае dQ/Т≤dS. Последняя формула — новое аналитическое выражение второго начала термодинамики применительно как к обратимым, так и к необратимым процессам. Функцию 5 Клаузиус считал мерой способности теплоты к превращению и дал ей название «энтропия». Это слово происходит от греческого слова «tpoitvj» (превращение). Клаузиус, так же как и Томсон, считал возможным распространить основные принципы термодинамики на всю Вселенную и, подобно Томсону, пришел к заключению о неизбежности ее тепловой смерти. «Можно,— писал Клаузиус,— оба главных положения механической теории теплоты сформулировать как основные законы вселенной в следующей простой форме. 1) Энергия мира постоянна. 2) Энтропия мира стремится к максимуму»10. Распространение второго закона термодинамики на необратимые процессы было завершающим шагом в установлении основ термодинамики. Термодинамика стала одной из важнейших областей физики, имеющей, с одной стороны, непосредственное значение для техники и, с другой стороны, играющей значительную роль в дальнейшем построении всего здания физической науки. Отношение к этой вновь возникшей области физических наук было противоречивым. Если первое начало термодинамики (после того как был признан закон сохранения энергии) не встречало возражений и вполне гармонировало с принятыми общими взглядами на физические явления, то иначе отнеслись физики ко второму началу, особенно в связи с распространением его на необратимые процессы. Новый принцип, как всякое новое открытие, не мог не встретить осторожного к себе отношения. Конечно, выводы из второго начала термодинамики об отношении между совершаемой работой и затраченным количеством теплоты (т. е. теорема Карно), количественное выражение коэффициента полезного действия тепловых машин и все вытекающие из этого следствия, поскольку они непосредственно подтверждались опытом и практикой, не вызывали сомнений и были приняты как физиками, так и инженерами. Иначе дело обстояло с обоснованием теоремы Карно. Много сомнений было высказано по поводу формулировки Клаузиусом невозможности процесса, единственным результатом которого являлся бы переход теплоты от менее нагретого к более нагретому телу. Конечно, никто не оспаривал того факта, что при тепловом контакте двух тел всегда происходит уравнивание температур путем перехода теплоты от тела с большей температурой к телу с меньшей температурой. Но Клаузиус (и Томсон) утверждал, что не может существовать никакого физического процесса, единственным результатом которого являлось бы нагревание какого-либо тела и одновременно охлаждение тела, имеющего меньшую температуру, чем первое. Такое утверждение было далеко не тривиальным и не могло не вызвать попытки обнаружить в природе явления, которые бы ему не подчинялись. Помимо простого недоверия к новому или, по крайней мере, критического отношения к нему было и другое обстоятельство, заставившее ряд ученых и философов - сомневаться в правильности нового закона природы Клаузиуса и Томсона. Новый физический закон утверждал неизвестную до тех пор односторонность протекания всех физически реальных процессов. Согласно ему, во всякой изолированной системе процессы должны всегда протекать в направлении постепенного превращения всех видов энергии в теплоту при одновременном уравнивании температурных разностей, существующих в системе. А это означало, что хотя энергия системы и оставалась строго неизменной, тем не менее с течением времени она лишалась способности к превращениям, а значит, и способности «совершать какую-либо работу», т. е. энергия «обесценивалась», «деградировала», в системе наступала тепловая смерть. Вывод о тепловой смерти в некотором смысле противоречил только что установленному закону сохранения энергии. Закон сохранения и превращения энергии воспринимался как закон, утверждающий неуничтожимость движения, неиссякаемость жизни в природе, а второе начало — неизбежность «деградации» энергии. Получалось, что энергия сохраняется лишь формально, так как, теряя способность совершать работу, она, по существу, переставала быть энергией, которая и понималась как способность совершать работу. Далее, неизвестная до этого времени «однонаправленность» течения всех реальных физических процессов противоречила механистическим взглядам физиков на эти процессы. Ведь сама термодинамика, казалось, укрепляла подобные взгляды. Действительно, она возникла только тогда, когда стало ясно, что теплота есть движение. Этим движением в конечном счете является, безусловно, механическое движение атомов и молекул. Но для механического движения не существует никакой временной односторонности в их протекании. Оно обратимо. Как же может в природе появиться необратимось, если в основе ее процессов лежат обратимые явления? Все эти вопросы были очень трудными, и для их разрешения потребовалось много времени и труда целого ряда исследователей. Наконец, казалось возможным распространить второй закон на всю Вселенную (что и сделали главные основоположники термодинамики). В этом случае он приводит к теории тепловой смерти, а значит, и к оправданию библейской легенды о сотворении и конце мира. Если для религиозно настроенных ученых и философов это являлось подтверждением их взглядов, то для материалистов такого рода выводы были совершенно неприемлемы. Естественно, что второе начало термодинамики, не говоря уже о теории тепловой смерти Вселенной, не могло не встретить возражений ряда физиков и философов. Английский физик Тэт впоследствии писал: «... рассеивание энергии не было ясно понято физиками. Многие результаты, сообщенные им, признавались только с трудом; их даже считали смешными»11. Естественно, что вскоре после опубликования работ Клаузиуса и Томсона в печати появляются возражения против всеобщности формулировки второго закона, данного этими учеными (эквивалентность их формулировок была сразу же выяснена). Уже в 1852 г. появилась первая работа, которая была посвящена опровержению теории рассеяния энергии, принадлежащая Ранкину. Ранкин не соглашался с выводом Томсона о неизбежности тепловой смерти Вселенной и высказывал гипотезу, как он полагал, опровергавшую конец мира. Согласно этой гипотезе, межзвездная среда (т. е. эфир) не простирается до бесконечности, а имеет за пределами видимого мира граничную сферическую поверхность, за которой находится пустое пространство. Вследствие этого тепловые лучи, в которые превращается рассеянная энергия, отражаются от этой поверхности и собираются в некоторых областях мирового пространства, как в фокусах, создавая там высокую температуру. Попадая в эти области, остывшая материя какого-либо небесного тела должна вновь нагреться, превратиться в раскаленную массу и образовать новые системы, подобные солнечной. Таким образом, одновременно с процессами гибели миров вследствие рассеяния энергии во Вселенной должны протекать процессы возникновения новых с последующим развитием на них жизни. Рассуждения Ранкина были подвергнуты критике со стороны Клаузиуса который показал их несостоятельность. При этом Клаузиус разобрал более конкретный вопрос применимости второго закона термодинамики к излучению. В частности, из соображений Клаузиуса следовало, что температура изображения излучающего источника должна быть меньше температуры тела самого источника. Таким образом, возражения Ранкина опровергались. Имели место и другие возражения против всеобщности второго закона термодинамики, ряд из которых разобрал сам Клаузиус. При этом он расширил и углубил понимание этого закона. В 1862 г. французский инженер Гирн, специалист в области термодинамики и теплотехники, высказал сомнение в истинности принципа Клаузиуса. Гирн придумал установку, в которой осуществлял процесс, с первого взгляда противоречащий второму началу термодинамики в формулировке Клаузиуса12. Эта установка (рис. 10) состояла из двух рядом расположенных цилиндров Либс теплоизолированными стенками, соединенных между собой тонкой трубкой. К поршням цилиндров были прикреплены зубчатые стержни, сцепленные между собой зубчатым колесом. Наполнив цилиндры газом при некоторой температуре (например, 0°С), приводят поршень в цилиндре В в крайнее нижнее положение, а соединительную трубку помещают в пары воды при температуре 100°С и медленно вращают зубчатое колесо так, чтобы поршень в цилиндре В поднимался, а в цилиндре А — опускался. Когда поршень в цилиндре В поднимется в крайнее верхнее положение, газ полностью перетечет из цилиндра А в цилиндр В. Гирн доказывает, что при этом температура газа будет выше 100°С. 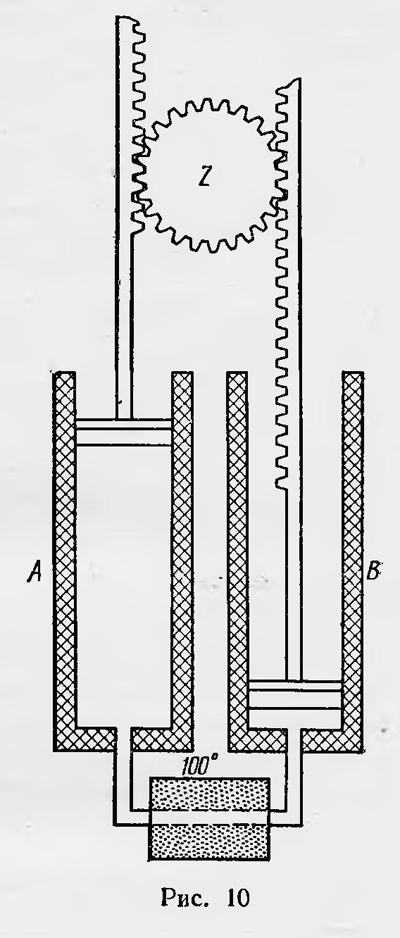
Действительно, каждая порция газа, проходя через соединительную трубку, нагревается до 100° С, при этом ее объем увеличивается, в результате повышается давление в каждом из цилиндров. При этом находящийся в цилиндрах газ подвергается адиабатическому сжатию и вследствие этого нагревается еще больше. Начальная температура газа в цилиндре В была равна 100°С (первую порцию газа нагревают до этой температуры), поэтому в конце процесса температура в этом цилиндре должна стать выше 100°С. Учитывая, что давление газа в обоих цилиндрах все время одинаковое, следовательно, никакой работы при движении поршней не производится, получаем окончательный результат всего процесса: газ нагревается до температуры более высокой, чем температура источника теплоты, что как будто противоречит постулату Клаузиуса. Клаузиус показал, что возражения Гирна ошибочны13. В опыте Гирна переход тепла от пара к газу идет все время, как указал Клаузиус, согласно его постулату, так как газ, проходя через трубку, в которой происходит теплопередача, имеет температуру всегда ниже температуры пара. Одновременно этот переход нужно рассматривать как компенсацию повышения температуры газа в цилиндре В выше температуры пара. 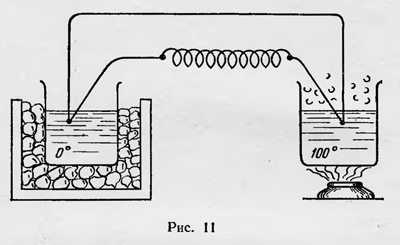
Против постулата Клаузиуса высказался Тэт14. Он привел пример с нагреванием тонкой проволоки, включенной в цепь термоэлемента, спаи которого помещены в тающий лед и кипящую воду (рис. 11). В этом случае, полагал Тэт, теплота, отдаваемая кипящей водой, частично проявляется опять-таки как теплота, выделяемая в проволоке. Поскольку проволока может иметь температуру значительно более высокую, чем температура кипящей воды, то в данном случае имеет место самопроизвольный переход теплоты от менее нагретого тела к более нагретому. Опровергая возражение Тэта, Клаузиус15 указал, что в данном случае переход теплоты от тела с меньшей температурой к телу с большей температурой осуществляется одновременно с процессом перехода тепла от кипящей воды ко льду, который компенсирует первый процесс, что находится в полном согласии с его постулатом. Кольрауш16 сомневался в обоснованности рассуждений Клаузиуса. Он указал, что компенсации процесса, проходящего в отрицательном направлении (т. е. передачи тепла от тела более холодного к телу более нагретому), процессом, проходящим в положительном направлении (т. е. передачей теплоты от тела с большей температурой к телу с меньшей температурой), в данном случае может и не быть, так как если второй процесс протекает при постоянной разности температур (100° С), то для первого процесса эта разница теоретически может быть, сколь угодно большой. Клаузиус разрешил сомнения Кольрауша, приведя дополнительные соображения17, которые в несколько модернизированном виде можно свести к следующему. Обозначим температуру льда через Т0; температуру воды — через T1, температуру проволоки — через Т2; количество теплоты, переходящее от воды ко льду за некоторый малый промежуток времени, — через dQ и количество теплоты, выделившееся за тог же промежуток времени в проводнике, — через q. Тогда общее изменение энтропии всей системы за данный промежуток времени можно записать так: 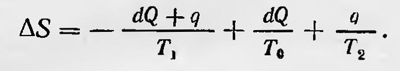
Принимая теперь, как и Кольрауш, что Т2 равно бесконечности, получаем, что изменение энтропии 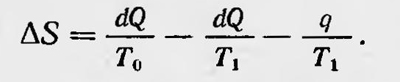
Постулат Клаузиуса требует, очевидно, чтобы ΔS≥0, что не приводит ни к какому парадоксу, как полагал Кольрауш. Наоборот, это неравенство может быть использовано для расчетов тепловых процессов в термоэлементе. В 1878 г. Престон18 выдвинул новое возражение против постулата Клаузиуса. Он рассмотрел явление диффузии газов через пористую перегородку. Если в цилиндре, который разделен подвижным поршнем из обожженной глины, поместить в отделенных поршнем частях кислород и водород, то водород будет сильнее диффундировать через глину, чем кислород. В результате в отделении, где помещен кислород, повысятся давление и температура, а в отделении, где находится водород, давление и температура понизятся. Таким образом, самопроизвольно создается не только разность температур, но и производится работа, если поршень может передвигаться. Это на первый взгляд противоречит формулировке второго начала, данной Клаузиусом. Клаузиус опроверг и это возражение19, указав, что в данном случае компенсацией создания разности температур является процесс смешения газов, т. е., говоря современным языком, уменьшение энтропии вследствие создания разности температур и давлений компенсируется возрастанием ее в результате диффузии. Одновременно с отрицанием всеобщего значения постулатов Клаузиуса и Томсона были сделаны попытки ввести новые положения, которые не имели бы такого революционного характера, но из которых можно было получить и теорему Карно, и остальные конкретные результаты термодинамики. В основном они сводились к попыткам доказать существование энтропии, т. е. показать, что выражение dQ/T - полный дифференциал для случая обратимых процессов. Ранкин уже в 1851 г., а затем в 1854 г. пытался построить термодинамику без постулатов Клаузиуса и Томсона. Вместо них он использовал положение о том, что dQ/T - полный дифференциал особой функции состояния. Это положение он считал возможным доказать, исходя только из первого закона термодинамики и из рассмотрения теплоты как молекулярного движения. В 1876 г. некто Этинген, будучи противником теории деградации энергии, утверждал возможность построения термодинамики без постулатов Клаузиуса или Томсона. Он полагал, что факт существования энтропии сможет следовать из первого закона термодинамики20. Однако все эти попытки оказались неудачными. Вопрос же о смысле второго закона термодинамики и выводов из него постепенно перешел в область молекулярной физики. В конце XIX в. и в первые десятилетия XX в. был поднят вопрос об обосновании термодинамики, отличном от обоснования данного Клаузиусом и Томсоном. Впервые по-новому к этому вопросу подошел русский физик Николай Николаевич Шиллер (1848—1910). Не отвергая постулатов Клаузиуса и Томсона, он искал логически более строгие постулаты, которые могли бы их заменить. В своей работе, посвященной этому вопросу, Шиллер писал: «... является возможным разыскать комбинацию опытных данных, может быть, более непосредственных, которая послужила бы к новой формулировке того же закона и вела бы к тем же следствиям, как и обе предыдущие»21. Рассматривая с общей точки зрения явление теплового обмена и изменение состояния термодинамической системы, Шиллер находит такую формулировку и предлагает ее в нескольких вариантах в частности таком: «При всяком обратимом адиабатном изменении тела, характеризуемом при помощи независимых друг от друга параметров, любой из вышеупомянутых параметров возвращается к своему первоначальному значению, коль скоро остальные п — 1 параметров возвращаются к своим. То есть: при упомянутом процессе каждый из параметров может быть определен однозначно через другие»22. В более поздней работе этот основной постулат Шиллер формулирует несколько иначе: «При обратимом адиабатном процессе каждый термический параметр рассматриваемого тела должен принять свое первоначальное значение, когда все остальные термические параметры тоже приходят к своим первоначальным значениям»23. Рассмотренный постулат позволяет, не пользуясь никакими конкретными представлениями о круговых процессах, предположить существование интегрирующего множителя для количества теплоты в общем случае так, что dQ=ΘdS, т. е. существование энтропии. При этом Θ — функция температур, возрастающая или убывающая вместе с температурой, — является мерой абсолютной температуры. «Аксиоматическое» направление в термодинамике продолжает развивать К. Каратеодори (1873—1950). В основу термодинамики он положил две основных аксиомы (1809). Первая из них составляет основу «первого начала» теории теплоты и является выражением общего принципа энергии»24. Вторая аксиома выражает второй закон термодинамики и формулируется следующим образом: «В любой окрестности произвольно заданного начального состояния имеются состояния, которые нельзя как угодно точно аппроксимировать адиабатическими изменениями состояния»25. Это и есть так называемый «принцип адиабатической недостижимости». Каратеодори. Из аксиомы Каратеодори следует существование энтропии и всех соответствующих следствий из этого факта. Каратеодори наряду с понятием обратимости вводит понятие квазистатичности. Квазистатичным изменением системы он называет такое изменение, при котором каждое последовательное состояние системы можно рассматривать как равновесное. Следующий шаг в развитии аксиоматического направления в термодинамике был сделан русским физиком Татьяной Алексеевной Афанасьевой-Эренфест (1876—1964). В ряде работ, опубликованных начиная с 1925 г.26, она показала, что второй закон термодинамики можно представить как два независимых положения (что уже намечалось в работах Каратеодори). Одно из них относится к факту существования энтропии и к квазистатическим процессам. Второе положение связанное с необратимыми процессами,—утверждает рост энтропии в замкнутых системах. Эти положения Афанасьева-Эренфест сформулировала в виде двухтрупп аксиом, которые могут быть положены в основу термодинамики. В 1926 г. в статье «Об основании второго закона термодинамики» Планк выступил с критикой аксиоматического направления в термодинамике, в частности против подобного разделения второго закона27. Не останавливаясь на этой статье, укажем, что дискуссия по этому вопросу продолжалась до последнего времени28. После установления основ термодинамики Клаузиусом, Томсоном и другими важным моментом в ее последующем развитии было исследование случаев термического равновесия, что привело к введению ряда функций — термодинамических потенциалов. Впервые понятие о таких функциях ввел Массье в 1869 г. Он показал, что термодинамические свойства тела постоянного состава могут быть выведены из рассмотрения некоторых особых функций, которые он назвал характеристическими29. Массье использовал две такие функции: 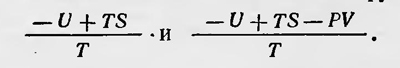
В 1882 г. Гельмгольц30, исследуя вопросы термодинамики химических процессов, ввел функцию F = U — TS. Эта функция, как показал Гельмгольц, для термодинамической системы, обладающей постоянной температурой (т. е при изотермических процессах), играет ту же роль, что и потенциальная энергия для механических систем. Именно:так называемые обобщенные силы А1 (давление, напряженность электрического или магнитного поля и т. д.) равны частным производным от функции F по обобщенным координатам а (объем, магнитный момент и т. д.), взятым с обратным знаком, т. е. 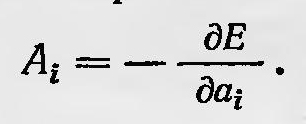
При этом работа, совершаемая системой при изотермическом процессе, равна уменьшению функции F, так что dW = —dF. Функцию F, определяющую запас работы, которую может произвести термодинамическая система при изотермическом процессе, Гельмгольц назвал свободной энергией. Свободная энергия, подобно потенциальной энергии в механике, определяет условие равновесия системы при неизменной температуре. Если учесть второе начало термодинамики для необратимых процессов, то, когда система не совершает работы, dF с 0. Отсюда следует, что если в системе происходят необратимые процессы, то свободная энергия ее уменьшается и стремится к минимуму, который достигается при равновесии, в этом случае dF — 0. Общая теория термодинамического равновесия, основанная на исследовании термодинамических потенциалов, была развита американским ученым Джозайя Уиллардом Гиббсом (1839—1903) в его работе «О равновесии гетерогенных веществ» (1875—1878). Для определения общего критерия термодинамического равновесия, по Гиббсу, можно воспользоваться либо энергией, либо энтропией системы в различных возможных состояниях. В соответствии с этим и критерий термодинамического равновесия, полагает Гиббс, можно формулировать одним из следующих способов31: «1. Для равновесия любой изолированной системы нробходимо и достаточно, чтобы при всех возможных изменениях состояния системы, не влияюишх на ее энергию, вариация энтропии исчезала или была отрицательна», т. е. (δη)ε≤0. «2. Для равновесия любой изолированной системы необходимо и достаточно, чтобы при всех возможных изменениях состояния этой системы, не влияющих на ее энтропию, вариация ее энергии исчезала или была положительная т. е. (δε)η≥0. От общих условий равновесия термодинамической системы Гиббс переходит к частным случаям и разрабатывает теорию термодинамических потенциалов. В работе Гиббса теория термодинамического равновесия доведена до высокой степени совершенства. Не случайна поэтому высокая оценка, данная этой работе. Так, например, Гааз писал, что Гиббс довел науку об общей термодинамике до той самой степени общности, до которой довели в более раннее время Лагранж и Гамильтон общую динамику32. 
Джозайя Уиллард Гиббс В заключение обзора развития термодинамики еледовало бы остановиться на так называемой проблеме тепловой смерти Вселенной, которую поставил и Томсон и Клаузиус. Однако, поскольку эта проблема неограничивается рамками термодинамики, а обсуждается и в рамках статистической физики, где была сделана первая попытка ее решения, остановимся на этой проблеме ниже, когда будем говорить об истории статистического толкования второго закона термодинамики. 1Clausius R. Ann. Phys., В. 79, 1850, S. 501. 2Там же, S. 503. 3Томсон В. О динамической теории теплоты.— В кн.: Второе начало термодинамики. М.—Л., ОНТИ, 1934, с. 165. 4Thomson W. Mathematical and Physical papers. Vol. 1. Cambridge. 1882, p. 235. 5Thomsom W. Mathematical and phusical papers. Vol I, p. 237. 6Clausius R. Ann. Phys., B. 93, 1854, S. 488. 7Клаузиус P. Механическая теория тепла.— В кн. Второе начало термодинамики, с. 134. 8Томсон В. О проявляющейся в природе общей тенденции к рассеянию механической энергии.— В кн.: Второе начало термодинамики., с. 182. 9Clausius R. Ann. Phys. В. 116, 1862, S. 74. 10Clausius R. Ann. Phys., В. 125, 1865, S. 400. 11Брюи Б. Деградация энергии и гибель Мира. Пг., 1915, с. 83. 12Нurn G. Exposition analitlque et experimental de la theorie mechanique qe la chaleur. Paris et Colmar, 1862. 13Clausius R. Die mechanische Warmetheorie. Braunschweig. 1876, S. 378. 14Tait P. Phil. Mag., (4). Vol. 43, 1872, p. 338. 15Clausius R. Die mechanische Warmetheorie S. 376—378. 16Kohlrausch F. Ann. Phys. Vol. 156, 1875, S. 600. 17Clausius R. Die mechanische Warmetbeorie. S. 378—382. 18Preston S. Nature. Vol. 17, 1878, p. 202. 19Clausius R. Die mechanische Warmetheorie. S. 378. 20Oettingen A. Ann. Phys. Erganz. VII, 1876, S. 84. 21Шиллер Н. Н. — ЖРФХО, 1898, т. 30, ч. физ., отд. 1, 2, с. 36. 22Там же., с. 37. 23Шиллер Н. Н. Основные законы термодинамики. Киев, 1903, с. 11. 24Каратеодори К. Об осноиах термодинамики.— В кн.: Развитие современной физики. М., «Наука», 1964, с. 196. 25Там же, с. 197. 26Zеitsсhr. f. Phys., 1925, В. 33, с. 933; Bd. 34, с. 638; Журнал прикладной физики, т. V, вып. 3—4, 1928, с. 33; Die Grundlagen der Thermodynamik, Leiden, 1956. 27Планк М. Об основании второго закона термодинамики.— В кн.: Вандер-Ваальс И. Д., Констамм Ф. Курс термодинамики М., ОНТИ, 1936, с. 438. 28См. по этому вопросу: Гельфер Я. М. История и методология термодинамики и статистической физики. Т. I. М., «Высш. школа», 1968. 29Мassiеu Т. F. r. Acad, sci, vol. 69, 1869, p. 858, 1037, 30Helmholtz H. Wissenschaftlichen, Abhandlungen. B. 11, Leipzig, 1883, S. 958. 31Гиббс Дж. В. Термодинамические работы. М.—Л., Гостехиздат, 1954, с. 96. 32A commentary In the scientific writings of J. Willard Gibbs. Vol. 1. New Haven, 1936, p. VII. |
загрузка...
