§ 63. Развитие электродинамики движущихся сред
Вопрос о влиянии движения тел на электромагнитные явления впервые затронул Максвелл. Если неподвижный проводник находится в переменном магнитном поле, то в проводнике возникает электрическое поле Е, которое определяется уравнением 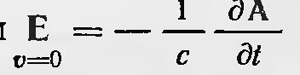 , где А—вектор-потенциал. Максвелл рассмотрел также случай, когда проводник движется в постоянном магнитном поле. Он изучает движение прямолинейного проводника вдоль двух параллельных прямолинейных же проводников и получает для этого простого случая выражение напряженности электрического поля в движущемся проводнике. Несложный расчет показывает, что в этом случае , где А—вектор-потенциал. Максвелл рассмотрел также случай, когда проводник движется в постоянном магнитном поле. Он изучает движение прямолинейного проводника вдоль двух параллельных прямолинейных же проводников и получает для этого простого случая выражение напряженности электрического поля в движущемся проводнике. Несложный расчет показывает, что в этом случае 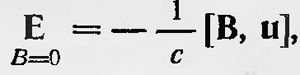 , где u - скорость соответствующей точки проводника. , где u - скорость соответствующей точки проводника.
В общем же случае движения проводника в переменном магнитном поле для напряженности электрического поля, появляющегося в проводнике, получаем выражение 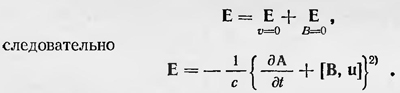 1 1
Последнее уравнение Максвелл вывел для движущегося проводника, но можно полагать, что он понимал его более широко. Это видно хотя бы из того, что без второго члена это уравнение представляет собой одну из форм записи второго основного уравнения электромагнитного поля, использованного затем Максвеллом для доказательства существования электромагнитных волн. В полном виде это уравнение Максвелл нигде не применял и не рассматривал специально задачи, относящиеся к электродинамике движущихся тел. Впервые уравнение электродинамики движущихся тел предложил Герц в 1890 г. При этом он опирался на гипотезу о том, что эфир, заключенный в телах, всегда движется вместе с ними, т. е., говоря другими словами, эфир полностью увлекается телами при их движении. Далее, он предположил, что если выбрать систему отсчета, связанную с движущимся телом, то в ней для электромагнитного поля действительны обычные уравнения Максвелла. Если же перейти к неподвижной системе отсчета, в которой движется тело, то здесь уже справедливы уравнения, отличные от уравнений Максвелла. Для того чтобы их получить, считал Герц, нужно предположить, что электрическое и магнитное поля определяются не просто изменением магнитного и электрического полей соответственно в какой-либо точке, связанной со средой, но и их изменением, вызванным движением среды вместе с эфиром. В этом случае вместо обычных производных δВ/δt и δD/δt следует брать так называемые субстанциональные производные. Субстанциональная производная от вектора R, как известно, равна 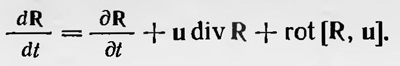
Подставляя в правую часть уравнения Максвелла вместо обычных производных субстанциональные и учитывая, что div В = 0, получаем два основных уравнения электродинамики движущихся тел Герца: 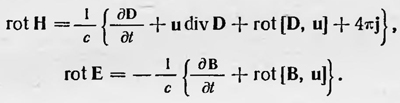
Другие уравнения электромагнитного поля для движущихся сред совпадают с таковыми для покоящихся тел. Естественно, что, получив уравнения электромагнитного поля для движущихся сред, Герц ставит вопрос о том, насколько они соответствуют эксперименту. Прежде всего он ссылается на опыт Роуланда, о котором уже упоминалось выше и который заключался в определении магнитного поля движущегося заряженного проводника. Роуланд брал эбонитовый диск А и помещал его между двумя стеклянными дисками а1 и а2 (рис. 27). Обе стороны эбонитового диска, так же как и внутренние стороны стеклянных дисков, он покрывал тонким слоем золота. Заряжая затем поверхности эбонитового диска электрическим зарядом (например, положительным) и соединяя поверхность стеклянных дисков .с землей, он приводит эбонитовый диск во вращение вокруг оси Ь1 Ь1, измеряя при этом магнитное поле у края эбонитового диска с помощью магнитной стрелки М. В опыте Роуланда ток проводимости и ток смещения отсутствуют, следовательно, 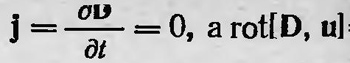 =0, так как среда, находящаяся между дисками, остается в покое, поэтому первое уравнение Герца в данном случае имеет вид =0, так как среда, находящаяся между дисками, остается в покое, поэтому первое уравнение Герца в данном случае имеет вид
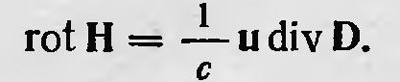
Если по этой формуле провести расчет, используя данные опытными результатами Роуланда. Таким образом, опыт Роуланда не противоречит теории Герца, и последний рассматривает его результаты как подтверждение своей теории. 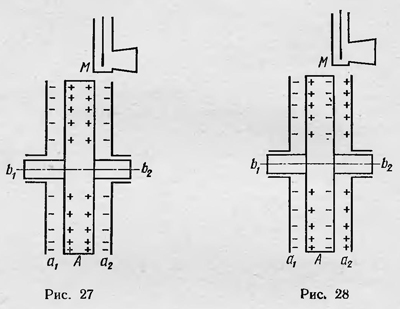
Герц также отмечает опыт Рентгена2, проделанный последним в 1888 г., по обнаружению магнитного поля, которое создается движущим диэлектриком в электрическом поле. В этом опыте (рис. 28) стеклянный или эбонитовый диск А, помещенный между обкладками конденсатора а1 и а2, приводится во вращение. Магнитная стрелка М, подвешенная вблизи одной из обкладок конденсатора, должна была фиксировать наличие магнитного поля, появление которого ожидалось в результате вращения диска А. Рентген действительно обнаружил наличие магнитного поля Н, однако точность его эксперимента не была достаточной для того, чтобы определить величину этого поля в зависимости от параметров установки и скорости вращения диска. Из уравнений Герца также следует, что вращающийся в электрическом поле диэлектрик должен создавать магнитное поле. Величина этого поля определяется из первого уравнения Герца при условии, что ток проводимости и ток смещения отсутствуют и udivD — 0, поскольку движущихся (обычных) зарядов нет. Отсюда rot Н = 1/c rot [D, u]. Однако, так как Рентген не получил количественных данных, результат этого опыта мог рассматриваться Герцем лишь как качественное подтверждение своей теории. Как это ни странно, но в своей работе Герц не затрагивает вопрос о применимости развитой им теории к оптическим явлениям в движущихся телах. Это тем более странно, что гипотеза Максвелла об электромагнитной природе света к этому времени получила экспериментальное подтверждение и не кто иной, как сам Герц, сделал в этом направлении первый решающий шаг. Он впервые наблюдал электромагнитные волны и показал, что они обладают всеми свойствами световых волн. Тем не менее Герц ограничивается в своих работах рассмотрением только чисто электромагнитных явлений, не затрагивая вопросы оптики движущихся тел, такие, как явление аберрации света, опыт Физо и т. д. Он даже не останавливается на результатах опыта Майкельсона, несмотря на то что мог бы найти в них подтверждение своей теории. Герц рассматривает свою теорию как одну из возможных, как теорию, имеющую, так сказать, поисковый, разведывательный характер. В связи с этим он пишет, что, вероятно, «правильная теория должна будет отличать для каждой точки состояние эфира от состояния заключающей его материи»3. Совершенно иначе к построению электродинамики движущихся тел подошел Лоренц. По Лоренцу, существует всюду неподвижный эфир, в котором движутся электрические заряды (и положительные, и отрицательные). В эфире распространяется электромагнитное возмущение, создаваемое зарядами и в свою очередь действующее на заряды. Электромагнитное поле, возбуждаемое зарядом и распространяющееся в эфире, подчиняется уравнениям Лоренца, а силы, которые действуют на заряды, определяются величиной силы Лоренца. Все это справедливо для покоящихся и движущихся тел. Но уравнение Лоренца справедливо для микрополей, мы же наблюдаем усредненные значения е и h. И только при усреднении необходимо различать случаи неподвижных и движущихся сред. Для неподвижных сред, как отмечалось, при усреднении получаются обычные уравнения Максвелла. В случае же движущихся сред Лоренц получает новые уравнения (уравнения Лоренца для движущихся сред). Для немагнитных сред они имеют вид: 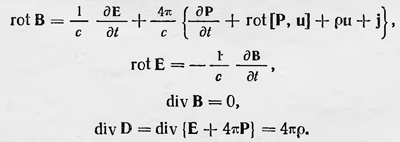
Здесь Р — вектор поляризации, равный 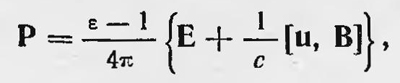
где ρ — плотность макроскопических свободных зарядов, u — скорость среды, для которой определяются Е и В. В отличие от Герца Лоренц применил развитую им теорию к оптическим явлениям в движущихся телах. За исключением результатов опыта Майкельсона, он объяснил все известные экспериментальные факты. Что касается опыта Майкельсона, то он как раз и предположил гипотезу сокращения. Таким образом, теория Лоренца имела явное преимущество перед теорией Герца. Конечно, было интересно проверить, как с точки зрения этой теории объясняются опыты Рѳуланда и Рентгена, на которые ссылается Герц, а также провести экспериментальные исследования, подобные этим опытам. Эту задачу выполнил русский физик Александр Александрович Эйхенвальд (1863—1944), который в 1901—1904 гг. провел целую серию экспериментальных исследований. Во-первых, он повторил опыт Роуланда и подтвердил справедливость результатов, полученных последним. Эти результаты, как отмечалось, находились в соответствии с теорией Герца. Однако они не противоречили и теории Лоренца. Действительно, для случая, который наблюдал Роуланд, первое уравнение Лоренца приводится к виду 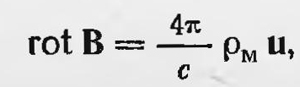
где ρм - плотность макроскопических зарядов. Учитывая, что 4πρм = divD и что в опыте Роуланда В — Н, получаем 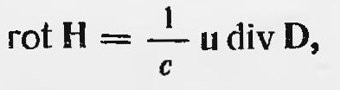
т. е. тот же самый результат, к которому приводит и теория Герца. Затем Эйхенвальд повторил опыт Рентгена и в отличие от последнего получил количественные результаты, которые уже позволяли сделать выбор между теорией Герца и теорией Лоренца. Согласно уравнениям Герца, движущийся диэлектрик в электрическом поле в магнитном отношении эквивалентен обычному току, плотность которого 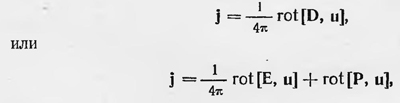
так как D = E + 4πP. В соответствии же с теорией Лоренца такому диэлектрику в магнитном отношении эквивалентен ток с плотностью j = rot[P,u], т. е. отличающийся на величину 1/4π[Е, и] от значения, которое получается из уравнений Герца. Это различие обусловливается тем обстоятельством, что, как полагает Герц, вместе с диэлектриком движется также и эфир, тогда как, по Лоренцу, эфир неподвижен, а движутся только поляризационные заряды. Измерения Эйхенвальда показали, что опыт согласуется с теорией Лоренца. 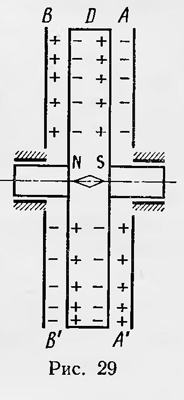
Эйхенвальд проделал также опыт, в котором измерял магнитное поле при движении диэлектрика в неоднородном электрическом поле. В опыте (рис. 29) эбонитовый диск D вращался между обкладками двух конденсаторов AB и А'В', каждый из которых состоял из двух пластин. Конденсаторы заряжались таким образом, что если, например, пластина А была заряжена отрицательно, а пластина В— положительно, то пластина А', наоборот, заряжалась положительно, а пластина В' — отрицательно. При вращении диска помимо тока, образуемого движущимися зарядами, появившимися в результате поляризации диэлектрика в тех местах, где электрическое поле меняло свой знак, возникал ток смещения, который также создавал магнитное поле. Из теории Герца следовало, что вместе с диском вращался и эфир, заключенный в нем. Поэтому ток смещения j=1/4π δD/δt = 1/4π δE/δt + δP/δt, тогда как, по теории Лоренца, магнитное поле вызывает только ток смещения в диэлектрике, который равен j =δP/δt. Измерения Эйхенвальда показали, что и в данном случае теория Герца дает неправильный результат, а теория Лоренца находится в согласии с экспериментом. Таким образом, экспериментальные исследования, проведенные Эйхенвальдом, решали вопрос в пользу теории Лоренца и, казалось, подтверждали гипотезу о том, что эфир должен быть неподвижным всюду, в том числе и внутри движущихся тел. Такой вывод и сделал Эйхенвальд. В 1904 г. он писал: «То, что мы называем в настоящее время мировым эфиром и что пронизывает собой все материальные тела, мы doлжны считать неподвижным daжe внутри самой материи, находящейся в движении»4. Как отмечалось, Лоренц в отличие от Герца основное внимание уделял оптике движущихся тел, рассматривая свет как распространение электромагнитного возмущения в неподвижном эфире. Его теория объясняет явление аберрации света, опыт Физо и опыты типа Араго, поставленные для определения движения Земли относительно эфира, имеющие точность порядка u/с. Рассматривая ряд оптических явлений в движущихся средах, Лоренц использует математический прием, заключающийся в замене переменных. Наряду с координатами х', у', z', связанными с движущимся телом (Землей), он вводит также взамен напряженностей электрического и магнитного полей Е и В новые переменные: Е' = Е + — [u, В] и В' = В + 1/c[Е, u], где u — скорость движения тела относительно эфира. Он также вводит переменную t' вместо времени t, называя ее «местным временем»: t' = t - ur'/c2. Оказывается, что в новых переменных уравнения Лоренца в случае отсутствия токов проводимости с точностью до величин (u/с)2 совпадают с уравнениями Максвелла, а именно: 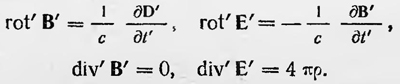
(Здесь rot' и div' означают, что производные берутся по х’, у', z'.) Таким образом, можно сказать, что данные преобразования с точностью до величин порядка (u/с)2 оставляют уравнения Максвелла инвариантными. Решение полученных уравнений известно для многих случаев. Написав решение для какого-нибудь случая и проделав обратную замену переменных, можно получить решение поставленной задачи. Используя этот прием, Лоренц находит, например, скорость распространения света в движущемся диэлектрике. Пусть имеется прозрачный диэлектрик с показателем преломления n, который движется вдоль оси х со скоростью u, и пусть в направлении его движения распространяется плоская электромагнитная волна. Для того чтобы определить скорость ее распространения, напишем уравнения для данного случая в переменных Е', В', х', t'. Для Е' решение имеет вид Е' = Е'0 tv'(t'-x'/c1) Если теперь перейти к неподвижной системе координат и к истинному времени t, то получим 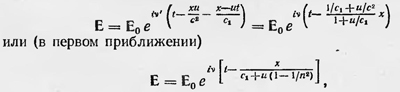
v = v' (1 + u/c1). Таким образом, мы приходим к выводу, что. в подвижной среде должна распространяться плоская волна со скоростью, равной с1+u(1—1/n2), т. е. со скоростью, которая получается согласно теории Френеля, что подтверждается опытом Физо. В качестве подтверждения гипотезы о неподвижности эфира Лоренц указывает также на экспериментальные исследования Лоджа, проведенные в 1891 г.5 Лодж наблюдал интерференцию двух пучков световых лучей, прошедших в противоположных направлениях между двумя параллельно расположенными дисками, которые были укреплены на общей оси. Сравнивая интерференционные картины для случаев, когда диски неподвижны и когда они быстро вращаются, Лодж не обнаружил смещения интерференционных полос. Этот результат можно было объяснить, признав, что эфир, находящийся между дисками, заметным образом не участвует в их движении. Оценив точность экспериментальных данных, Лодж заключил, что диски не сообщают эфиру даже 0,005 доли своей скорости. Единственный опыт, относящийся к исследованиям оптических явлений в движущихся телах, при объяснении которого Лоренц встретился с серьезным затруднением, был опыт Майкельсона. Для его объяснения, как говорилось выше, Лоренц и ввел гипотезу о сокращении тел в направлении их движения в эфире. Он полагает, что если предположить, что, подобно электрическим взаимодействиям, молекулярные силы также передаются через эфир, то их величина будет зависеть от движения тел так же, как зависят электрические и магнитные силы от движения зарядов. Что же касается зарядов, то уже было известно, что электрическое поле движущихся зарядов зависит от их скорости и изменяется в соответствии с гипотезой о сокращении. В 1900 г. английский физик Дж. Лармор (1857—1942) сделал новый шаг в развитии электродинамики движущихся сред6. Он, как и Лоренц, рассматривал электромагнитные и оптические явления в движущихся телах с точки зрения электронной теории (в развитии которой он имеет определенные заслуги). Лармор считал, что все тела состоят из заряженных частиц, которые являются особыми точками в неподвижном и заполняющем все пространство эфире. Силы, действующие между частицами, имеют электромагнитный характер и определяются значениями электрических и магнитных полей, которые описываются уравнениями электромагнитного поля Как и Лоренц, Лармор считает эфир всюду неподвижным и для объяснения отрицательного результата опыта Майкельсона применяет гипотезу сокращения. Он математически «оформляет» эту гипотезу, применяя метод преобразования координат, времени и полей для эфира. Он сначала вводит те же преобразования, что и Лоренц, которые сохраняют инвариаитными уравнения Максвелла с точностью до величин второго порядка малости величины ѵ/с для эфира, т. е. для вакуума. Лармор применяет еще и второе преобразование координат, времени и полей, которое обеспечивает полную инвариантность уравнений Максвелла. Если объединить эти два преобразования и записать их в современном виде, то для простейшего случая переносного движения вдоль оси х они имеют вид7: 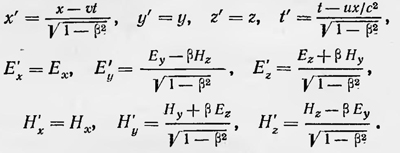
Пусть теперь имеется система зарядов, находящихся в «устойчивом» состоянии и образующих макротело. Пусть эта система как целое приобретает движение в эфире. Тогда она по-прежнему будет находиться в устойчивом состоянии и составлять то же макротело, только расстояние между электрическими зарядами должно уменьшаться в 1/(√1-ß2) раз. В самом начале XX в. были проделаны новые опыты, в которых движение тел относительно эфира, как и в опыте Майкельсона, можно обнаружить с точностью порядка ѵ2/с2. В 1902 г. Релей, а в 1904 г. Брее пытались обнаружить двойное лучепреломление в прозрачных изотропных телах, обусловленное сокращением их размеров в направлении их движения вместе с Землей. Это сокращение, по их мнению, должно иметь место в соответствии с гипотезой Фитцджеральда — Лоренца. В 1903 г. Трутон и Нобль предприняли попытку определить движение Земли относительно эфира, пытаясь измерить момент силы, который мог бы действовать на заряженный конденсатор, движущийся вместе с Землей в эфире, плоскость которого расположена под углом к направлению движения. Но все эти опыты, как и опыт Майкельсона, дали отрицательный результат: эфирный ветер на Земле не был обнаружен. Результаты новых опытов побудили Лоренца вернуться к вопросам электродинамики движущихся тел и обобщить ранее разработанную теорию, что он и сделал в 1904 г. в работе «Электромагнитные явления в системе, движущейся с любой скоростью, меньшей скорости света». В основе теории лежит гипотеза, которая является развитием гипотезы сокращения. Она состоит из двух предположений. Во-первых, Лоренц считает, что размеры всех частиц, составляющих тела, при движении последних в эфире изменяются в направлении этого движения в 1/(√1-ß2) раз. Так, электрон, имеющий сферическую форму, превращается в сплющенный эллипсоид. Во-вторых, Лоренц полагает, что все силы, которые действуют между частицами, образующими тело, также изменяются соответствующим образом. Основываясь на этих предположениях, Лоренц показал, что никакие оптические или электромагнитные опыты не только первого, но и второго порядка относительно ѵ/с, произведенные в движущейся системе, не в состоянии обнаружить ее движение относительно эфира. При доказательстве этого положения Лоренц опять использует математический прием преобразования переменных. Лоренц ищет такие формулы преобразования координат, времени, полей и других переменных, входящих в формулы электронной теории, которые оставляли бы последние инвариантными. До конца эту задачу Лоренц в данной работе не решил. Он не нашел правильные формулы для преобразования плотности электрического заряда р и скорости и. В движущейся системе координат формулы электронной теории при таких преобразованиях для случая движения вдоль оси х имели вид: 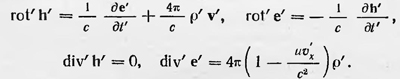
Таким образом, уравнение dive = 4др не оставалось точно инвариантным при преобразованиях, установленных первоначально Лоренцем (выражение для силы также не оставалось инвариантным). Однако, несмотря на указанные недостатки, Лоренц доказал, применяя прием преобразования координат, времени и полей, что не существует опытов, с помощью которых можно было бы определить движение тел относительно эфира, т. е., можно сказать, установил «практический принцип относительности». 
Анри Пуанкаре Французский математик и физик Анри Пуанкаре (1854—1912) обратился к проблемам, рассмотренным Лоренцем. В отличие от последнего Пуанкаре сразу исходил из принципа относительности, который он распространил на оптические и любые явления природы. В 1905 г. в краткой статье, помещенной в июньском номере «Comptes rendus»8, он, исходя из принципа относительности, уточнил формулы преобразования Лоренца и показал полную инвариантность уравнений электромагнитной теории относительно уточненной системы преобразований, которые он и назвал преобразованиями Лоренца. Нужно отметить, что еще раньше в своих выступлениях и статьях Пуанкаре говорил о принципе относительности как общем законе природы. Так, в докладе на Всемирном конгрессе физиков в Париже в 1900 г. он высказал мнение, что отрицательный результат опыта Майкельсона является выражением общего закона природы. Согласно этому закону, все «оптические явления должны зависеть только от относительного движения материальных тел источников света и оптических инструментов и это верно не только для величин порядка квадрата аберрации, но абсолютно точно»9. В 1904 г. в своей речи на международном конгрессе в Сент-Луисе Пуанкаре назвал принцип относительности в числе основных принципов физики. Согласно этому принципу, говорил Пуанкаре, «... законы физических явлений будут одинаковыми как для покоящегося наблюдателя, так и для наблюдателя, находящегося в состоянии равномерного поступательного движения, так что мы не имеем и ие можем иметь никаких средств, чтобы различить, находимся ли мы в таком движении или нет»10. В отмеченной выше работе Comptes Rendus Пуанкаре указывал на принцип относительности как на всеобщий закон природы. Он писал: «Невозможность обнаружить абсолютное движение Земли представляет, по-видимому, общий закон природы»11. Следуя именно этому принципу, Пуанкаре и пришел к необходимости исправления преобразований Лоренца для плотности зарядов и скорости. В этой работе, а также в более подробной статье, вышедшей в следующем, 1906 г.12, Пуанкаре выясняет ряд следствий из общих положений, связанных с принципом относительности. Некоторые из них легли затем в основу математического аппарата теории относительности. Так, например, Пуанкаре устанавливает, что преобразования Лоренца образуют группу. Он показывает, что при таких преобразованиях величина «интервала» х2+у2+z2—с2t2, а также значение Е2— Н2 остаются инвариантными. В качестве математического приема Пуанкаре вводит в рассмотрение четырехмерное пространство, в котором три координаты соответствуют обычным пространственным координатам, а четвертая является мнимой координатой времени. В этом пространстве он представляет преобразования Лоренца как поворот осей. Пуанкаре ставит вопрос о том, какое влияние должен оказать принцип относительности на теорию гравитации, и приходит к выводу, что из принципа относительности следует конечность скорости распространения силы тяготения и что скорость эта должна равняться скорости света. Теория Лоренца — Пуанкаре еще не была, строго говоря, теорией относительности, как ее создал Эйнштейн. Это была теория электромагнитных явлений в движущихся телах, основанная на старых представлениях об эфире, дополненная новыми гипотезами. Ближе всего к основным представлениям теории относительности подходил Пуанкаре, который в разработке математического аппарата был даже впереди Эйнштейна. Но он не решился на полный разрыв с общими классическими представлениями, хотя и был близок к нему. Насколько близок был Пуанкаре к этому, свидетельствуют его соображения, высказанные по поводу измерения времени и понятия одновременности событий. Еще в 1898 г. Пуанкаре обратил внимание на вопрос измерения времени и понятия одновременности событий. В работе «Измерение времени» он отметил, что понятие направления времени, равномерного его течения и понятие одновременности событий пока еще не подвергались научному анализу. В основе этих понятий лежали интуитивные представления о том, что время течет равномерно во всех точках пространства. Однако анализ понятий приводит к другим выводам. Пуанкаре рассматривает различные способы определения течения времени и одновременности для удаленных событий. В частности, он рассматривает и случай использования световых сигналов. Здесь Пуанкаре подчеркивает, что для определения одновременности двух удаленных событий следует принять постулат постоянства скорости света во всех направлениях. Это именно постулат, так как он экспериментально не доказуем и не опровергаем, так как мы можем измерять скорость света, измеряя только время прохождения его «туда и обратно», т. е. среднюю скорость. В результате существует произвол в определении скорости света в одном направлении. Следовательно, имеется определенный произвол и в определении одновременности двух удаленных событий. Таким образом, понятие одновременности — понятие относительное. Для того чтобы устранить этот произвол, вводят постулат постоянства скорости света в различных направлениях, как наиболее простое предположение. Пуанкаре пишет: «Одновременность двух событий или порядок их следования, равенство двух длительностей должны определяться таким образом, чтобы формулировка законов природы была бы настолько простой, насколько это возможно. Другими словами, все эти определения являются лишь плодом неосознанного соглашения»13. После работы Лоренца, опубликованной в 1904 г., о которой говорилось выше, Пуанкаре уже связывает вопрос измерения времени и одновременности с оптикой движущихся тел. В статье «Настоящее и будущее математической физики», вышедшей в свет в 1904 г., Пуанкаре рассматривает часы, находящиеся в пунктах А и Б. Для того чтобы эти часы шли одинаково, нужно их отрегулировать. Для этого используются световые сигналы. Если световые сигналы, вышедшие из пунктов А и В навстречу друг другу, в момент, когда находящиеся в этих пунктах часы показывают время 0, приходят соответственно в пункты В и А, когда часы в них показывают одно и то же время t, то следует считать, что часы отрегулированы и сверены между собой. Однако если пункты А и В движутся, то вследствие конечной скорости распространения света сверенные таким образом часы уже не будут показывать «истинное время», как говорит Пуанкаре. Например, если пункт А движется навстречу световому сигналу, выходящему из пункта В, а пункт В удаляется от возмущения, исходящего из пункта В, то часы в пункте А будут отставать от часов, находящихся в пункте В. Но в этом случае часы в пунктах А и В показывают так называемое «местное время», которое входит в формулы преобразования Лоренца. Принцип относительности требует, чтобы это местное время невозможно было бы отличить от истинного. «Все явления, которые произойдут в А, например, будут запаздывать, но запаздывать одинаково,— пишет Пуанкаре,— и наблюдатель не заметит этого, потому что его часы отстают, таким образом, как того требует принцип относительности, у наблюдателя не будет никакого способа узнать, находится ли ой в покое или в абсолютном движении»14. Таким образом, мы видим, как близко подошел Пуанкаре к пониманию физического содержания теории относительности. Однако он не до конца проанализировал понятие одновременности. Пуанкаре различает истинное время и местное время, считает возможным использовать понятие абсолютного движения, рассматривая его как движение относительно неподвижного эфира и т. д. В сентябре 1905 г., спустя год после появления работы Лоренца, в немецком журнале «Annalen der Physik» появилась работа Эйнштейна «К электродинамике движущихся тел». Эйнштейн сформулировал основные положения специальной теории относительности, которая приводила к тем же конкретным результатам, что и теория Лоренца — Пуанкаре, для электромагнитных явлений в движущихся телах, но одновременно содержала новый взгляд на пространство и время. 1В это уравнение Максвелл добавлял еще третий член (grad φ), который здесь опущен. 2Röntgen W. Ann. Phys. В. 35, 1883, S. 264. 3Нertz Н. Ann. Phys. В. 41, 1890, S. 399. 4Эйхенвальд А. А. Избранные работы. М., Гостехиздат, 1956, с. 11. 5Lodge О. Phil Trans. (A). Vol. 184, 1893, p. 727 6Lаrmоr J. Aether and Matter Cambridge, 1900 7Лармор применяет векторы D и В, но для данного случая (вакуума) эти векторы совпадают с Е и Н. 8Роіnсаre H. C. r. Acad. Sei. Vol. 140, І905, p. 1504. См. также: Пуанкаре А. Избранные труды. Т. III. М., «Наука», 1974, с. 429. 9Poincare Н, Rapports presentes au Congres Internationa] de Physique гёипі ä Paris en 1900, t. I. Paris, 1900, p. 22. 10Poincare H. The Monist. Vol. 15, 1905, p. 5. 11Пуанкаре А. Избранные труды. Т. III, с. 429. 12Роіnсаre H. Rendiconti del Circalo. Matematico di Palermo, vol. 21, 1906, p. 129. См. также: Пуанкаре А. Избранные труды. Т. III, с. 433. 13Пуанкаре А. Избранные груды. Т. III, с. 428. 14Пуанкаре А. Избранные труды. Т. III, с. 566. |
загрузка...
