§ 62. Развитие оптики движущихся тел

Впервые вопрос о влиянии движения источников света и приемников, регистрирующих световые сигналы, на оптические явления возник в связи с открытием аберрации света английским астрономом Брадлеем в 1728 г. Наблюдая за неподвижными звездами, Брадлей заметил, что они представляются с Земли не совсем неподвижными, а описывают в течение года малые замкнутые траектории на небесной сфере. Придерживаясь тогдашнего общего мнения о справедливости корпускулярной теории света, Брадлей очень просто объяснил это явление. Если световая частица падает на поверхность Земли под углом а, то, для того чтобы наблюдать ее в центре поля зрения телескопа, его нужно наклонить на некоторый угол 6 в направлении движения Земли. Причиной является движение телескопа вместе с Землей, в результате которого за то время, пока световая частица движется внутри трубы телескопа, весь телескоп вместе с окуляром перемещается вместе с движением Земли. В простейшем случае, когда направление движения световой частицы и направление движения Земли составляет прямой угол, угол аберрации вычисляется по простой формуле

tg δ = ѵ/с,

где ѵ — скорость движения Земли по орбите, с — скорость света.

Измерив величину аберрации, точнее, изменение угла аберрации в течение года и зная скорость движения Земли по орбите, Брадлей подсчитал скорость света. Он получил для с величину, близкую к полученной ранее Ремером из наблюдений за движением спутников Юпитера.

Вторым вопросом, относящимся к оптике движущихся тел, который подвергся рассмотрению, был вопрос о возможном влиянии движения тела на преломление в нем света, испускаемого неподвижными небесными источниками. С точки зрения корпускулярной теории казалось вполне естественным предположить, что показатель преломления тела, движущегося относительно источника света, должен зависеть от скорости движения. Действительно, ведь в случае движения преломляющего тела световая частица встречает это тело со скоростью, которая зависит от скорости этого движения. Показатель же преломления тела должен определяться только скоростью световых частиц относительно преломляющего тела. Поэтому, например, казалось вполне возможным ожидать, что фокусное расстояние линзы, измеренное с помощью света, который испускался земным источником, неподвижным относительно линзы, отличается от такового, если для измерения использовать свет от звезд. Мнение о наличии такого эффекта было высказано еще в XVIII в. В 1810 г. Араго поставил опыт, с помощью которого рассчитывал определить, изменяется ли показатель преломления призмы в случае использования света от звезд в результате движения Земли. Был получен отрицательный результат: разница в показателе преломления при различной скорости движения Земли относительно звезд не наблюдалась¹. Объясняя этот факт, Араго выдвинул гипотезу, согласно которой светящееся тело испускает световые частицы со всевозможными скоростями, из которых только частицы, обладающие определенными скоростями относительно человеческого глаза, вызывают в нем ощущение света. Однако если свет, воспринимаемый движущимся наблюдателем, всегда должен иметь одну и ту же скорость относительно него, то он должен также всегда и преломляться одинаково приборами, движущимися вместе с наблюдателем.

Обсуждение результатов опыта Араго и вообще вопроса о влиянии движения источников и приемников света происходило уже в рамках волновой теории света. Нужно подчеркнуть, что вопрос о влиянии движения источников и приемников света на оптические явления для волновой теории света был значительно более сложным, чем для теории, основанной на представлении о корпускулярной природе света. Решение его требовало введения ряда гипотез. Нужно было определенным образом предположить: как взаимодействуют весомые тела и эфир (полагали, что эфир проникает в тела); отличается ли эфир внутри тел от эфира, находящегося вне их, и если отличается, то чем; как ведет себя внутри эфир тел при их движении, и т. д.

Юнг, возродивший волновую теорию света в начале XIX в., коснулся в своих работах и вопросов, относящихся к оптике движущихся тел. Уже в 1804 г. он отметил, что явление аберрации света может быть объяснено волновой теорией света, если предположить, что эфир повсюду, в том числе и внутри движущихся тел, остается неподвижным. В этом случае явление аберрации объясняется, как и в корпускулярной теории света.

Однако гипотеза Юнга о неувлекающемся эфире не могла объяснить результата опыта Араго, и поэтому Френель, который заинтересовался результатами опыта Араго, отказался от гипотезы Юнга. Но Френель не мог принять и противоположную гипотезу о том, что эфир полностью увлекается движущимся телом. Эта гипотеза не могла бы объяснить явление аберрации света. Френелю пришла очень интересная идея о частичном увеличении эфира движущимися телами. Используя эту гипотезу, он сумел объяснить и явления аберрации света, и отрицательный результат, полученный в опыте Араго.

Напомним, что согласно основным предположениям Френеля эфир внутри весомых тел отличается от эфира вне этих тел только своей плотностью, что же касается упругих свойств эфира, то они везде одинаковы. Если р — плотность эфира внутри тела, а р0 — плотность эфира в пространстве, где нет весомых тел, то по Френелю, существует соотношение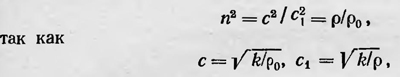

где k — величина, характеризующая упругие свойства эфира, а с и с₁ — соответственно скорость света в вакууме и в данном теле.

Гипотеза Френеля заключается в том, что тело при своем движении увлекает только ту часть эфира, находящегося внутри него, которая составляет избыток плотности в нем по сравнению с плотностью в пространстве, свободном от весомых тел, т. е. часть, равную ρ — ρ₀. Определив теперь скорость эфира w, находящегося внутри движущегося тела, как скорость движения его центра масс относительно эфира вне тела, Френель в результате простых вычислений приходит к формуле

w=(1-n/n²)u,

где u — скорость данного тела относительно окружающего неподвижного эфира.

Таким образом, скорость света относительно неподвижного эфира, т. е. абсолютная скорость света в движущемся теле, равна

c₁+(1-1/n²)u,

где с₁ — скорость света в теле, когда оно неподвижно.

На основе предложенной гипотезы Френель объясняет опыт Араго. Он показывает, что если при расчете² влияния движения призмы на преломление света пренебречь величинами порядка ѵ²/с² и выше, то такое влияние отсутствует. Таким образом, хотя движение Земли и должно оказывать влияние на показатель преломления тел, движущихся вместе с ней, тем не менее это влияние слишком мало, чтобы его можно было обнаружить.

Френель пишет, что и другие оптические опыты, поставленные на Земле, практически не могут быть использованы для определения движения Земли относительно эфира. Он рассматривает следующий опыт. На продолжении оптической оси зрительной трубы, наполненной водой, помещают неподвижно скрепленный с ней точечный источник света так, чтобы он был четко виден в трубу. Трубу располагают так, чтобы ее оптическая ось была перпендикулярна плоскости эклиптики, и совмещают изображение источника света с крестом нитей, помещенном в трубе. Затем всю трубу вместе с источником света поворачивают на 180° и наблюдают, произойдет ли смещение изображения по отношению к кресту нитей. Проведя расчет на основе гипотезы частично увлекающегося эфира, Френель показывает, что порядок величины ожидаемого смещения изображения источника света должен быть таким же, как и в опыте Араго, т. е. его практически невозможно обнаружить. Таким образом, и этот опыт не может быть использован для определения движения Земли относительно эфира.

В дальнейшем Лоренц привел общее доказательство того, что движение относительно эфира не оказывает влияния на любые оптические явления с точностью до второго порядка величины ѵ/с.

В середине 40-х годов английский ученый Стокс разработал новую теорию аберрации. Он исходил из предположения, что Земля при своем движении полностью увлекает окружающий ее эфир, так что скорость эфира на поверхности Земли в точности равна ее скорости. Помимо этого, он предположил, что движение эфира, увлекаемого Землей, является безвихревым во всем пространстве,окружающем Землю,вплоть до областей, где он пребывает в покое. Такое предположение также объясняет явление аберрации света. Помимо этого, оно позволяет объяснить и отрицательный результат, полученный в опыте Араго. Из него также следует, что в любых оптических опытах, проведенных на Земле, не может быть обнаружена скорость ее движения. Сравнивая свою теорию с теорией Френеля, Стокс указывал, что эти теории хотя и основываются на противоположных гипотезах, но практически приводят к одним и тем же результатам. Были проделаны и другие опыты, имевшие целью обнаружить скорость движения Земли относительно эфира. Они также не дали положительных результатов и также объяснялись и теорией Стокса и теорией Френеля, поскольку их точность была недостаточной для обнаружения эффекта порядка (v/c)².

В 1851 г. француз И. Физо провел опыт, который склонял чашу весов в пользу теории Френеля. Он заключался в измерении скорости света в текущей воде. Физо установил влияние движения воды на скорость распространения в ней света, а также что в пределах ошибок эксперимента можно полагать его подтверждением теории частичного увеличения эфира Френеля. В 1886 г. Майкельсон и Морли проделали аналогичный опыт со значительно большой точностью и подтвердили выводы Физо. Результаты проделанного опыта Физо расценил как бесспорное подтверждение теории Френеля и опровержение теории Стокса. Однако опыт Физо свидетельствовал только, что обычные прозрачные тела небольших размеров при своем движении частично увлекают эфир. Однако вопрос о том, что происходит с эфиром, когда в нем движется такое огромное тело, как Земля, — еще нельзя было считать решенным.

В 60-х годах проблемой определения движения Земли относительно эфира заинтересовался Максвелл. Он повторил опыт Араго в более точном варианте и также получил отрицательный результат. В 1868 г.

Альберт Майкельсон

Максвелл сообщил о проделанном опыте, а также о своих теоретических соображениях, касающихся вопросов оптики движущихся сред, а затем он вернулся к этому вопросу в конце жизни. Рассмотрев состояние проблемы о поведении эфира при движении в нем весомых тел, в том числе и Земли, Максвелл пришел к заключению, что имеющийся экспериментальный материал хотя и говорит больше в пользу теории Френеля, чем теории Стокса, тем не менее еще не может считаться достаточным подтверждением первой. Он писал:

«... весь вопрос о состоянии светоносной среды возле Земли и об ее отношении к обыкновенной материи еще не решен опытом»³.

Максвелл рассмотрел вопрос о возможности постановки опыта, который мог бы однозначно решить, какая из существующих теорий является справедливой. Это опыт, в котором измерялась бы скорость света, идущего от земного источника на движущейся Земле в направлении ее движения, и затем сравнивалась со скоростью света, измеренной в противоположном направлении. Очевидно, что если земля не увлекает при своем движении окружающий эфир, то в первом случае эта скорость равна с₁=с—ѵ=с(1—ѵ/с), а во втором случае с₂=с(1+ѵ/с), где ѵ — скорость Земли. Таким образом, разница в скорости света в первом и втором случаях первого порядка малости относительно ѵ/с. Однако для проведения такого опыта нужно уметь измерять время, необходимое для прохождения светом известного расстояния в определенном направлении, например в направлении движения Земли. А эта задача экспериментально неразрешима. Поэтому во всех проводимых на Земле опытах по определению скорости света эта скорость определяется по времени, которое требуется для прохождения светом расстояния в прямом и обратном направлениях. Следовательно, для того чтобы определить влияние движения Земли на скорость света, остается возможность сравнить время прохождения светом определенного расстояния L туда и обратно один раз вдоль движения Земли, а другой раз, например, в направлении, перпендикулярном этому движению. Однако в этом случае разница во времени в первом и втором случаях является величиной уже второго порядка малости относительно ѵ/с, т. е. величиной порядка ѵ²/с².

Таким образом, хотя принципиально с помощью эксперимента и можно решить вопрос о поведении эфира при движении Земли, тем не менее вследствие малости величины ѵ²/с²≈10^-8 ожидаемый эффект должен быть чрезвычайно мал. В связи с этим Максвелл скептически высказывается по поводу практической возможности решения данного вопроса с помощью подобного эксперимента. Тем не менее такой эксперимент был вскоре (уже в 1881 г.) осуществлен американским физиком Альбертом Майкельсоном (1852—1931). Для сравнения времени прохождения в прямом и обратном направлениях света вдоль движения Земли и в направлении, перпендикулярному этому движению, Майкельсон воспользовался явлением интерференции. Он сконструировал специально, для этой цели интерферометр, известный под названием интерферометра Майкельсона (рис. 25).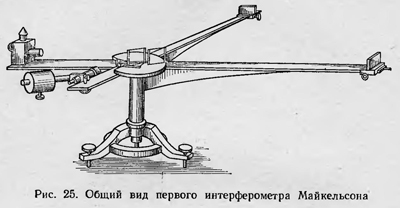

Интерферометр Майкельсона представляет собой два зеркала А и В и полупрозрачную пластинку D, расположенные, как показано на рис. 26. Луч света от источника 5 делится пластинкой D на два луча 1 и 2, которые после отражения от зеркал В и А, а также отражение луча 2 от пластинки D попадают в зрительную трубу Т. Положение интерференционных полос, наблюдаемых в зрительную трубу, определяется разностью хода, которую лучи 1 и 2 приобретают за время, в течение которого они проходят соответственно пути от пластинки D до зеркал А и В и обратно и которые можно считать одинаковыми и равными 2L.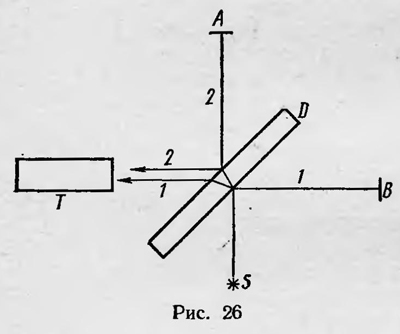

Пусть теперь интерферометр расположен так, что луч 1 двигается вдоль движения Земли, а луч 2 — перпендикулярно. Тогда если эфир не увлекается движением Земли, то время прохождения лучом 1 соответствующего пути равно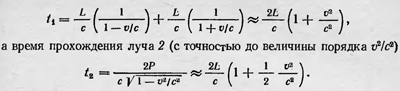

Таким образом, лучи 1 и 2 затрачивают разное время на прохождение расстояния 2L и разница во времени равна

t₁-t₂=Δt=L/c v²/c².

Если теперь повернуть весь прибор на 90°, то, наоборот, время, затрачиваемое лучом 1, равно 2L/c(1+1/2 v²/c²),а время прохождения луча 2 составляет —— 2L/c(1+v²/c²), разность их

t₁-t₂=Δt=-L/c v²/c².

В результате интерференционные полосы, наблюдаемые в трубу, сместятся, и хотя это смещение определяется величиной порядка v²/c², тем не менее его можно заметить. Следовательно, измерив смещение полос, можно определить и скорость эфирного ветра на Земле, или скорость движения ее относительно эфира.

Интерферометр, который использовал Майкельсон в первом опыте, был несовершенным, тем не менее он ожидал обнаружить эффект движения Земли. Из его расчетов следовало, что смещение интерференционных полос, если считать скорость ѵ равной орбитальной скорости Земли, должно быть равно 0,04 расстояния между соседними полосами. Однако он мог констатировать, что смещение не превышает 0,015 расстояния между соседними полосами, что можно объяснить ошибками наблюдения. Таким образом, опыт, как расценил его Майкельсон, приводит к отрицательному результату: эфирный ветер на Земле не обнаружен. Отсюда он сделал вывод, что окружающий Землю эфир увлекается ее движением и что, следовательно, правильной является гипотеза Стокса.

Однако Лоренц в 1886 г. возразил против такого вывода. Он указал, что в расчетах Майкельсона допущена ошибка и что на основании результатов его опытов можно сделать следующее заключение: ожидаемое смещение в случае наличия эфирного ветра должно быть вдвое меньше, т. е. почти в пределах ошибок измерения. Следовательно, результат рассмотренного опыта Майкельсона не свидетельствует об отсутствии эфирного ветра на Земле, так как ошибки наблюдения слишком велики. Самое большее, что можно предположить, по Лоренцу, — это то, что скорость эфирного ветра на Земле не больше половины ее орбитальной скорости.

Лоренц также рассмотрел теорию Стокса и высказал возражение. Нельзя, как показал Лоренц, сохраняя предположение о несжимаемом эфире, полагать, что скорость эфира у поверхности Земли точно равна ее скорости, а с другой стороны, считать, что движение эфира является безвихревым. Однако если нельзя сохранить ни гипотезу Стокса, ни гипотезу Френеля о поведении эфира у поверхности Земли, то можно считать, что хотя эфир у поверхности Земли и не остается неподвижным, но скорость его не совпадает со скоростью Земли. Тогда возможно полагать движение эфира безвихревым и объяснить явление аберрации света. Такая гипотеза, являющаяся в некотором роде комбинацией гипотез Френеля и Стокса, не противоречит и результатам опыта Майкельсона, если принять, что скорость движения эфира у поверхности Земли не больше половины скорости ее движения. Вскоре Лоренц был вынужден отказаться от этой гипотезы. В 1887 г. Майкельсон совместно с Морли опубликовал результаты нового опыта, являющегося повторением опыта, проведенного Майкельсоном в 1881 г. Введя целый ряд усовершенствований, они значительно повысили точность измерений и показали, что относительная скорость Земли и эфира, вероятно, меньше 1/6 орбитальной скорости Земли и несомненно меньше 1/4 этой скорости. Результаты нового эксперимента уже с гораздо большей степенью достоверности свидетельствовали, что на поверхности Земли никакого заметного эфирного ветра не наблюдается.

Таким образом, в оптике движущихся тел возникли серьезные противоречия. С одной стороны, имелась теория Френеля, которая объясняла многие экспериментальные факты, но противоречила результатам опыта Майкельсона. С другой стороны, теория Стокса объясняла результаты этого опыта, но не могла объяснить явление аберрации света. Фитцджеральд и независимо от него Лоренц высказали в 1892 г. гипотезу о сокращении размеров тел в направлении их движения относительно эфира. Согласно этой гипотезе, размеры тел при движении в эфире уменьшаются в направлении движения в

раз. Эта гипотеза совместно с гипотезой неувлекаемого, всюду неподвижного эфира объясняла отрицательный результат опыта Майкельсона. Подтверждением гипотезы сначала являлся отрицательный результат, полученный в опыте Майкельсона. Позже Лоренц дал этой гипотезе более основательное обоснование, исходя из общих представлений развитой им теории оптических и электромагнитных явлений в движущихся телах.

Важным вопросом, относящимся к оптике движущихся тел, был вопрос, рассмотренный впервые австрийским ученым Доплером (1803— 1853). Рассматривая свет как распространяющиеся волны возмущений в эфире⁴, Доплер отметил, что частота световых колебаний ѵ, воспринимаемых наблюдателем, зависит как от скорости источника света ѵ, так и от скорости наблюдателя и, взятых относительно эфира, и что она должна отличаться от частоты ѵ₀ световых колебаний, которые излучаются светящимся источником. Проведя простые рассуждения, он вывел формулу частоты воспринимаемого наблюдателем света: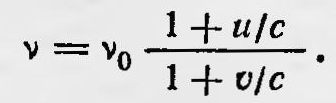

В скором времени выводы Доплера подвергли опытной проверке (для звуковых явлений). Экспериментальные исследования подтвердили теорию Доплера: тон источника звука, воспринимаемый наблюдателем, действительно оказался зависящим от скорости движения и источника звука и наблюдателя. Иначе дело обстояло с применением принципа Доплера к оптическим явлениям, для которых, собственно говоря, он и проводил свои рассуждения. На первых порах роль этого принципа в оптических явлениях подверглась оживленной дискуссии.

Сам Доплер с самого начала правильно считал, что с помощью открытого им принципа можно определять лучевые скорости движения небесных тел. Однако предложенный им метод был ошибочным. Доплер полагал, что спектр, излучаемый звездой, является спектром белого света и практически весь лежит в видимой части, т.е. интенсивность лучей в инфракрасной и ультрафиолетовой областях незначительна. Если принять эту гипотезу, то красная или фиолетовая часть спектра, который излучает небесное тело, находящееся в движении, должна пропадать вследствие того, что весь спектр сдвигается в фиолетовую или красную область и небесное тело должно приобретать красный или фиолетовый оттенок. В результате звезда, излучающая, вообще говоря, белый свет, должна казаться нам окрашенной в красный или фиолетовый цвет, что и дает возможность, по Доплеру, определять ее скорость относительно наблюдателя, находящегося на Земле.

В 1848 г. Физо впервые указал правильный метод использования принципа Доплера для определения лучевой скорости движения небесных светил. Он обратил внимание на открытие Фраунгофером в спектре Солнца и других небесных тел темных линий. Эти линии соответствуют определенным длинам волн, излучаемых светящимся телом, поэтому при движении последнего они должны смещаться в спектре, который наблюдает неподвижный наблюдатель. Измеряя смещение этих линий, как полагал Физо, можно определить лучевые скорости движения небесных тел. Метод Физо оказался правильным и был использован в астрономии.

В 1852 г. с возражениями в адрес Доплера выступил Петцваль⁵. Он отрицал правильность выводов Доплера и не признавал выдвинутый им принцип, предлагая свой «принцип сохранения периода колебаний». Для обоснования своих возражений Петцваль рассматривал случай, когда источник возмущений и их приемник (или наблюдатель), являются неподвижными, а вся среда находится в стационарном движении.Однако в данном случае применение принципа Доплера приводит к тем же результатам, на которых настаивал Петцваль, так как при этом u=ѵ, следовательно, ѵ=ѵ₀. Петцваль считал, что его выводы противоречат принципу Доплера. Он даже высказал сомнение о том, что акустические опыты действительно подтверждают теорию Доплера, и полагал, что изменение тона звучащего инструмента в результате его движения или движения воспринимающего этот тон наблюдателя можно объяснить помимо принципа Доплера. Между Петцвалем и Доплером возникла дискуссия⁶, в ходе которой были затронуты и некоторые общие вопросы методологического характера. Противники по-разному понимали существо физических законов, установленных наукой. Смысл этого спора в несколько модернизованном виде сводится к следующему. Петцваль считал, что физический закон должен быть сформулирован как чисто объективный закон природы в том смысле, что в нем не должны фигурировать величины, зависящие от восприятий наблюдателя или даже от средств наблюдения и состояния приборов. Закон, полагал он, должен иметь инвариантную форму по отношению к любым средствам наблюдения и приборам, которые используют при этом. Поэтому Петцваль отрицал принцип Доплера, который, как он полагал, говорил о субъективных восприятиях наблюдателей, и не считал его физическим законом.

Доплер, наоборот, утверждал, что в формулировке каждого физического закона должны фигурировать величины, которые измеряются на опыте. При этом он ссылался на авторитет Бэкона, Ньютона и других ученых и философов — основоположников экспериментальной науки и считал, что Петцваль рассуждает в духе старой схоластической философии. Поскольку на опыте, по Доплеру, в случае движения источника звука или наблюдателя всегда обнаруживается изменение тона, постольку принцип, устанавливающий это изменение, должен считаться одним из законов природы.

Спор между Доплером и Петцвалем продолжался недолго, так как ошибочность возражений последнего была очевидна. Прекратилось и обсуждение общих методологических вопросов, поднятых в этом споре. Эти вопросы стали злободневными значительно позже и были поставлены вновь в несравненно более острой форме в связи с дискуссией, развернувшейся вокруг понимания теории относительности, а затем и квантовой механики.

В 1887 г. Фогт⁷ опубликовал работу, посвященную исследованиям принципа Доплера. В этой работе он применил новые математические идеи, которые, как оказалось в дальнейшем, являются выражением некоторых основных положений специальной теории относительности.

Математически явление Доплера можно рассматривать как результат преобразования координат, как переход от системы координат х, у, z, непосредственно связанной со средой, в которой распространяются упругие возмущения, к системе координат х', у', z', связанной с движущимся наблюдателем или с источником упругих колебаний.

Так, например, пусть вдоль оси х в положительном направлении распространяется плоская синусоидальная волна возмущений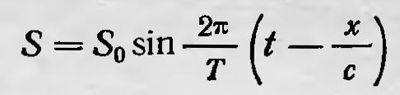

и наблюдатель движется вдоль той же оси со скоростью ѵ. Чтобы определить период колебаний, воспринимаемых наблюдателем, подставим в выражение для S координаты, которые связаны с движущимся наблюдателем (х' — х — vt, у' = у, z' — z). Тогда получим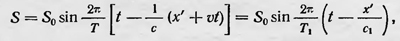

где c₁=c(1-v/c), a T₁=T/(1-v/c) — период колебаний, который, согласно принципу Доплера, воспринимает движущийся наблюдатель.

В своей работе Фогт предложил общий метод рассмотрения принципа Доплера. Он показал, что с математической точки зрения этот принцип можно рассматривать как результат преобразования переменных, входящих в уравнение распространения упругих возмущений более общего характера, а именно наряду с преобразованием пространственных координат х, у, z он вводит преобразование времени, заменяя переменную t на t'. Формулы преобразования координат и времени должны быть такими, чтобы волновое уравнение, описывающее процесс распространения возмущений в упругой среде: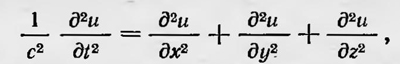

в новых переменных х', у', z' имело бы тот же самый вид, т. е.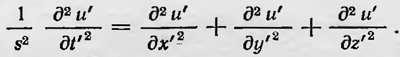

Исходя из этого условия, Фогт выводит формулы преобразования координат и времени, которые позволяют сохранить инвариантность волнового уравнения. Для простейшего случая переносного движения системы координат вдоль оси х со скоростью ѵ эти формулы имеют вид:

х' = х — vt, у' = βy, z' = βz, t’ = t - v/c² x,

где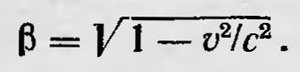

С помощью последних формул Фогт решает некоторые задачи на применение принципа Доплера. Он не придавал сколько-нибудь принципиального значения полученным формулам преобразования, рассматривая их как чисто математический прием и используя их для решения вопросов, связанных с явлением Доплера. Работа Фогта не обратила на себя внимания и о ней вспомнили после возникновения теории относительности. Нужно также отметить, что формулы преобразования, полученные Фогтом, отличаются от формул преобразований, установленных затем Лоренцем и положенных в основу теории относительности. Тем не менее, как в этом нетрудно убедиться, волновое уравнение действительно остается инвариантным при преобразованиях Фогта, так же как и при преобразованиях Лоренца.

Вообще, формулы преобразования, не изменяющие вид волнового уравнения, как было показано позднее Н. А. Умовым⁸, должны иметь для рассмотренного выше случая вид:

x' — a(x — vt), у' = βy, z' = βz, t' = a(t — v/c² x),

где а — произвольная функция от ѵ, а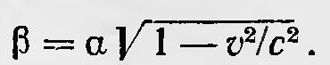

.

Очевидно, что и формулы преобразования Фогта, и формулы преобразования Лоренца — частный случай этих более общих формул. Если положить а — 1, то мы придем к формулам преобразования Фогта. Если же принять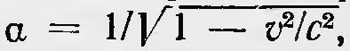

то эти формулы принимают вид формул Лоренца.

¹Отметим, что опыт Араго был бы, по-видимому, недостаточно точен для обнаружения искомого эффекта, даже если бы он и существовал.
²Расчет Френеля приведен в комментариях к его избранным сочинениям. См.: Френель О. Избранные работы по оптике, с. 507.
³Максвелл Дж. К. Статьи и речи. М., «Наука», 1968, с. 202.
⁴Будучи сторонником волновой теорив света, Доплер, однако, не признавал, что свет есть распространение поперечных волн в эфире, он считал световые волны продольными и рассчитывал, что дальнейшее развитие науки подтвердит эту точку зрения.
⁵Petzval J. Sitzungsber Acad Wiss„r Wien. В. 8, 1852, S. 134.
⁶Fortschr. der Phys., 8. Jahrg., 1855, S. 167.
⁷Voigt W. Nachrichten Wiss. Göttingen, 1887, S. 41..
⁸

<<Назад Вперёд>>

Просмотров: 4448

загрузка...

Другие книги по данной тематике