§ 64. Развитие представлений о пространстве и времени в физике до Эйнштейна

Физики долгое время придерживались взглядов Ньютона на пространство и время и нередко повторяли его определения понятий абсолютного пространства и времени. Только со стороны некоторых философов различных направлений понятие абсолютного пространства и времени подверглось критике.

Так, например, понятие пустого пространства критиковал современник Ньютона английский философ-материалист Джон Толанд, который считал бессодержательным само понятие пустого пространства:

«... я не могу поверить в абсолютное пространство, отличное от материи и вмещающее ее в себе, как не могу поверить и в абсолютное время, отличное от вещей, о длительности которых идет речь»¹.

С позиций идеализма понятие абсолютного пустого пространства критиковал Дж. Беркли. Отрицая объективность материального мира, он также отрицал объективность пространства и времени. Понятие пространства для Беркли есть лишь понятие, выражающее сосуществование идей. Это понятие может иметь только относительный смысл. Поэтому он отвергает понятие абсолютного пространства и времени как понятия, лишенные смысла, которые являются пустыми словами. Содержательным понятием, по его мнению, является только понятие относительного пространства.

Николай Иванович Лобачевский

При этом Беркли выступал против использования понятия абсолютного движения; о движении, считал он, можно говорить только как об относительном.

Однако критика Ньютона со стороны философов XVIII в., а также высказываемые ими взгляды на пространство и время, отличавшиеся от взглядов Ньютона, существенной роли для изменения конкретных представлений об этих понятиях среди физиков не сыграли. Последние фактически продолжали пользоваться представлениями Ньютона о физическом пространстве и времени, признавая или не признавая наличие пустого пространства.

Долгое время молчаливо предполагалось, что свойства физического пространства являются свойствами евклидового пространства. Для многих это была азбучная истина, особенно для тех, кто разделял взгляды Канта на пространство и время, который, как мы видели, считал, что пространство и время есть только необходимая форма чувственного созерцания, доопытная форма чувственного восприятия «вещи в себе». Из этого взгляда следовало, что те представления о пространстве и времени, которые уже существуют и которые выражены в представлениях геометрии Евклида и механики Ньютона, являются единственно возможными, так как определяются неизменными свойствами нашего разума.

Впервые по-новому вопрос о свойствах пространства был поставлен в связи с открытием неевклидовой геометрии. Безуспешность попыток ряда ученых многих поколений доказать пятый постулат Евклида привела к возникновению идеи о его недоказуемости, а вместе с тем и о возможности построения геометрии, основанной на других постулатах. Одним из первых пришел к этой идее Гаусс, который еще в начале XI Хв. начал размышлять над вопросом о возможности, другой, неевклидовой, геометрии. При этом он разошелся с Кантом во взглядах на пространство. Гаусс высказал мысль, что представления о свойствах пространства не являются априорными, а имеют опытное происхождение.

«Я прихожу все более к убеждению,—писал Гаусс,— что необходимость нашей геометрии не может быть доказана, по крайней мере человеческим рассудком и для человеческого рассудка. Может быть, в другой жизни мы придем к другим взглядам на природу пространства, которые нам теперь недоступны. До тех пор геометрию приходится ставить не в один ранг с арифметикой, существующей часто a’priori, а скорее, с механикой...» ².

Однако Гаусс, не желая быть втянутым в дискуссию, скрывал от современников свои идеи о возможности неевклидовых геометрий и не публиковал работы, относящиеся к этому вопросу.

В 1826 г. Николай Иванович Лобачевский (1792—1856) сделал сообщение на заседании физико-математического факультета Казанского университета об открытии им неевклидовой геометрии, а в 1829 г. опубликовал в «Казанском вестнике» работу «Начала геометрии». В этой работе, а также в ряде других Лобачевский впервые показал, что можно построить непротиворечивую геометрию, отличную от всем известной и признанной геометрии Евклида, которая ранее казалась единственно возможной. Через несколько лет, в 1832 г., венгерский математик Янош Больяй опубликовал работу, в которой независимо от Лобачевского развил основные идеи неевклидовой геометрии. Хотя Лобачевский и называл свою геометрию «воображаемой», тем не менее считал, что вопрос о том, законам какой геометрии подчиняется реальное пространство — геометрия Евклида или геометрии Лобачевского, — должен решить опыт.

«Напрасное старание со времени Евклида, в продолжение двух тысяч лет, заставило меня подозревать,— писал Лобачевский, что в самых понятиях еще не заключается той истины, которую хотели доказывать и которую проверить, подобно другим физическим законам, могут лишь опыты, каковы, например, Астрономические наблюдения»³.

Лобачевский полагал, что свойства пространства определяются свойствами материи и ее движения.

«В природе,— писал он,— мы познаем собственно только движение,без которого чувственные впечатления невозможны... все прочие понятия, например Геометрические, произведены нашим умом искусственно, будучи взяты в свойствах движения; а потому пространство, само собой, отдельно, для нас не существует. После чего в нашем уме не может быть никакого противоречия, когда гмы допускаем, что некоторые силы в природе следуют одной, другие своей особой Геометрии»⁴.

Спустя более чем 25 лет после того, как Лобачевский сделал сообщение об открытии им неевклидовой геометрии, Риман в 1854 г. прочел лекцию «О гипотезах, лежащих в основании геометрии», которая была напечатана в 1868 г. В лекции Риман, подобно Лобачевскому, опирался на идею о возможности геометрии, отличной от евклидовой, однако подошел к этому вопросу с несколько иных позиций. Риман вводит обобщенное понятие пространства как непрерывного многообразия n-го порядка или совокупности однородных объектов — точек, определяемых системой чисел (x₁, х₂, ..., х_n). Обобщая понятия созданной Гауссом геометрии поверхностей в обычном трехмерном пространстве, Риман пользуется для характеристики многообразия п-го порядка понятием расстояния между бесконечно близкими точками ds и понятием кривизны для каждой точки этого многообразия. В указанной работе он ограничился рассмотрением пространств постоянной кривизны, для которых расстояние между двумя бесконечно близкими точками может быть приведено к виду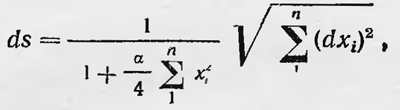

где α — кривизна пространства.

По мнению Римана, вопрос о том, является ли геометрия нашего физического пространства евклидовой, что соответствует его нулевой кривизне, или эта кривизна не равна нулю, должен решить эксперимент. Вообще же, по Риману, свойства пространства должны зависеть от материальных тел и процессов, которые в нем происходят.

Риман также высказал как одну из возможных гипотезу, касающуюся бесконечности пространства. По его мнению, хотя пространство нужно признать неограниченным, однако если оно может иметь положительную постоянную кривизну, то оно уже не бесконечно, подобно тому как поверхность сферы хотя и не ограничена, но тем не менее ее размеры не являются бесконечными.

Геометрия, которую создали Лобачевским и Больяй, в первое время имела весьма мало сторонников. Новая теория, которая противоречила воззрениям, установившимся в течение многих веков, не могла, конечно, быстро получить признание. К тому же представления, лежащие в основе работ Лобачевского и Больяй, противоречили взглядам Канта, которые пользовались в то время определенным авторитетом.

Перелом в отношении к геометрии Лобачевского наступил только в конце 50-х годов XIX в. Здесь важную роль сыграли работы итальянского математика Бельтрами, который показал, что планиметрия Лобачевского может быть реализована в евклидовом пространстве как внутренняя геометрия поверхностей постоянной отрицательной кривизны. Оживший интерес к геометрии Лобачевского, а затем и к работе Римана вызвал многочисленные исследования в области неевклидовых геометрий и основания геометрии вообще. В результате этих исследований во второй половине XIX в. были созданы новые области математики.

Доказательство непротиворечивости неевклидовых геометрий и их правомерности наравне с евклидовой опровергло учение Канта о пространстве. Вопреки мнению последнего оказалось, что представления о действительных свойствах реального пространства не априорны, а являются обобщением многовекового опыта человечества. Это обстоятельство было подчеркнуто Гельмгольцем. В одной из своих работ он писал, что признание возможности существования неевклидовых пространств опровергает мнение Канта о том, что «аксиомы геометрии суть необходимые следствия априорно данной трансцендентальной формы наших наглядных представлений, в смысле Канта»⁵. Наши знания о свойствах пространства, подчеркивал Гельмгольц, есть «не что иное, как эмпирическое знание, приобретенное путем накопления и усиления однородно возобновляющихся впечатлений, а никак не трансцендентальная и данная до всякого опыта форма созерцания»⁶.

Развитие теории пространств, геометрические свойства которых отличны от свойств обычного евклидова пространства, привело к вопросу о построении механики в таких пространствах. Первые работы в этом направлении были связаны с вопросом, не противоречит ли геометрия Лобачевского принципам механики? Если бы удалось доказать невозможность построения механики в неевклидовом пространстве, то тем самым была бы опровергнута мысль о возможности реального неевклидова пространства. Однако результаты, полученные в этом направлении, показали, что в неевклидовом пространстве может быть построена механика.

Однако все же появление неевклидовой геометрии, а затем «неевклидовой механики» первоначально не затронуло физику. Для физиков пространство оставалось евклидовым и не было никакой необходимости рассматривать физические явления в неевклидовом пространстве. Так продолжалось до возникновения общей теории относительности, когда основные идеи и математический аппарат неевклидовой геометрии вдруг оказались в центре внимания физиков. Правда, следует отметить, что открытие неевклидовой геометрии приводило иногда к возникновению и совершенно новых физических идей, получивших свое развитие позже. Так, английский математик Клиффорд в 70-х годах высказал идею⁷, что многие физические законы могут быть объяснены тем, что отдельные области пространства подчиняются неевклидовой геометрии. Он даже предложил нечто вроде полевой теории материи, в которой материальные частицы представляют собой сильно искривленные области пространства. Они подобны «холмам» на ровней местности, и перемещение этих частиц есть не что иное, как перемещение такого «холма» от одной точки к другой. При этом Клиффорд считал, что «в физике нет ничего иного, кроме изменений кривизны пространства». Дж. Уилер, приводя эти слова Клиффорда, видит в нем предшественника Эйнштейна, его полевой теории материи⁸.

Другое направление в развитии общих представлений о пространстве и времени заключалось в критике и пересмотре взглядов Ньютона на существование абсолютного движения как движения относительно абсолютного пространства относительно некой абсолютной системы отсчета.

Под влиянием авторитета Ньютона подавляющее большинство физиков XVIII и первой половины XIX в. соглашались со взглядами Ньютона на абсолютное и относительное движение. Однако начиная со второй половины XIX в. понятие абсолютного движения начинает подвергаться внимательному рассмотрению. Прежде всего предпринимается попытка придать понятию абсолютного пространства и абсолютной системы отсчета новое научное содержание, очистив эти понятия от того метафизического смысла, который придал им Ньютон.

В 1870 г. К. Нейман⁹ ввел понятие α-тела, как такого тела во Вселенной, которое является неподвижным и которое можно считать за начало абсолютной системы отсчета. Томсон и Тэт в своем неоднократном переиздававшемся фундаментальном курсе физики¹⁰ предложили принять за α-тело такое тело, которое совпадает с центром тяжести всех тел во всей Вселенной, полагая, что этот центр тяжести можно считать находящимся в абсолютном покое.

Однако вопреки таким мнениям все чаще и чаще высказывались соображения о том, что само понятие абсолютного прямолинейного и равномерного движения как движения относительно некоего абсолютного пространства лишено всякого научного содержания. Вместе с этим лишается содержания понятие абсолютной системы отсчета и вводится более общее и научное понятие инерциальной системы отсчета, не связанное с понятием абсолютного пространства. Так, например, Штрейнц в «Физических основах механики»¹¹ утверждает, что понятие абсолютной системы координат бессодержательно. Все системы, связанные со свободными телами, не находящимися под влиянием каких-либо других тел, равноправны.

В 1886 г. Л. Ланге, проводя исторический анализ развития механики и утверждая бессодержательность понятия абсолютного пространства, предложил определение инерциальной системе координат.

«Инерциальной системой.— писал Ланге,— назынаегся координатная сис іема, по отношению к которой траектории, описываемые гремя одновременно вышедшими из одного и того же пункта пространства точками и затем предоставленными самим себе, будут прямолинейными»¹².

Наиболее крайний взгляд на вопрос об относительности пространства и движения вообще высказал Мах в конце XIX в. Положение об относительности инерциального движения не затрагивает вопроса об относительности движения вообще. Если принять, что о скорости (как и о положении) всякого тела имеет смысл говорить только по отношению к другим телам, то, согласно классической механике, для того чтобы судить об ускорении, достаточно самого тела, испытывающего ускорения. Так, например, в случае с вращающимся ведром, в котором налита вода, можно говорить о его вращении самом по себе, безотносительно к другим телам. Значит, ускорение — величина абсолютная и может рассматриваться относительно пространства, а не относительно других тел. Этот вывод и оспаривал Мах. Он писал:

«Для меня вообще существует только относительное движение, и я не могу здесь допустить какую-нибудь разницу между движением вращательным и поступательным. Если тело вращается относительно неба неподвижных звезд, то развиваются центробежные силы, а если оно вращается относительно какого-нибудь другого тела, а не относительно неба неподвижных звезд, то таких центробежных сил нет. Я ничего не имею против того, чтобы первое вращение называли абсолютным, если только не забывают, что это означает не что иное, как относительное вращение относительно неба неподвижных звезд. Можем ли мы удержать неподвижным сосуд с водой Ньютона, заставить вращаться небо неподвижных звезд и тогда доказать отсутствие центробежных сил?

Опыт этот неосуществим, сама мысль о нем вообще не имеет никакого смысла, ибо оба случая чувственно не могут быть отличены друг от друга. Я считаю поэтому оба ад уча я за один и тот же случай и различение Ньютона за иллюзию»¹³.

В связи с этим Мах рассматривал системы Птолемея и Коперника как равноправные, считая последнюю более предпочтительной из-за простоты.

«Оба учения,— писал он,— также одинаково правильны, но последнее (учение Коперника.— Б. С.) только проще и практичнее»¹⁴.

Взгляды Маха на относительность всякого движения были связаны с его общими философскими принципами. Не признавая абсолютного пространства Ньютона, он не признавал объективного существования пространства вообще.

«... пространство и время,— писал Мах,— .. представляют собой в физиологическом отношении особые роды ощущений, а в физическом отношении — функциональные зависимости друг от друга элементов, охарактеризованных чувственными ощущениями»¹⁵), и в другом месте: «Пространство и время суть хорошо упорядоченные системы рядов ощущений»¹⁶.

В связи с такими взглядами на пространство и время для Маха было чуждым представление о движении относительно пространства. Поэтому всякое движение относительно пространства для него не имеет никакого смысла. О движении, по Маху, можно говорить только по отношению к телам. Поэтому все величины, определяющие состояние движения, являются относительными. Значит, и ускорение — также чисто относительная величина. На эту точку зрения Маха современные ему физики либо мало обращали внимания, либо выступали с критикой. Так, например, М. Планк в статье «Теория физического познания Эрнста Маха» (1910) весьма резко отозвался о рассуждениях Маха, назвав их путаными. Он писал:

«Мах не в состоянии усвоить тот огромный прогресс в науке, которым мы обязаны мировоззрению Коперника. Уже одного этого факта достаточно, чтобы набросить тень сомнения на теорию познания Маха»¹⁷.

Однако, как оказалось в последующем, несмотря на идеалистический подход к проблеме относительности движения, в соображениях Маха были некоторые интересные идеи, которые, способствовали появлению общей теории относительности¹⁸.

Комплекс вопросов об абсолютном пространстве и абсолютном движении приобрел новый смысл в связи с развитием электронной теории и возникновением гипотезы об электромагнитной природе материи. Согласно электронной теории Лоренца и его взглядам, разделявшимся многими физиками, как отмечалось, существует неподвижный всюду эфир и движущиеся в нем заряды. Неподвижный эфир заполняет все пространство и с ним можно связать систему отсчета, которая является инерциальной и, более того, выделенной из всех инерциальных систем отсчета. Движение относительно эфира можно рассматривать как абсолютное. Такая точка зрения действительно возникла и получила определенное развитие. Именно согласно этой точке зрения опыт Майкельсона начали понимать как опыт, призванный определить абсолютное движение Земли.

Таким образом, на смену абсолютного пространства Ньютона пришел неподвижный эфир, который можно рассматривать как своего рода абсолютную и к тому же инерциальную систему отсчета. Однако такая точка зрения уже с самого начала испытывала принципиальные затруднения. Об абсолютном движении тела, т. е. движении относительно эфира, можно говорить и представить, но определить это движение невозможно. Опыт Майкельсона и подобные ему опыты, поставленные с целью обнаружения такого движения, дали отрицательные результаты. Таким образом, хотя абсолютная система отсчета и была, как казалось, найдена, тем не менее она, как и абсолютное пространство Ньютона, оказалась ненаблюдаемой.

Лоренц для объяснения результатов, полученных в этих опытах, вынужден был ввести специальные гипотезы, из которых следовало, что, несмотря на существование эфира, движение относительно него определить невозможно. Пуанкаре пошел еще дальше. Он сформулировал принцип относительности для всех физических явлений, который утверждал равноправность всех инерциальных систем отсчета не только для механических явлений, но и для электромагнитных и вообще для всех физических явлений. Однако, как мы видели выше, Пуанкаре остался на старых позициях, разделяя взгляды Лоренца на существование эфира. И только Эйнштейн в 1905 г. подошел к решению этой проблемы с совершенно новой точки зрения, которая привела его к созданию теории относительности.

¹Толанд Дж. Письма к Серене. Избранные сочинения. М. — Д., 1927, с. 105.
²Об основаниях геометрии.— Сб. классических работ по геометрии Лобачевского и развитию ее идей. М., Гостехиздат, 1956, с. 103.
³Лобачевский Н. И. Полн. собр. соч. Т. 2. М. —Л, Гостехиздат, 1949, с. 147.
⁴Там же с. 158—159.
⁵Гельмгольц Г. Означении и происхождении геометрических аксиом.— В кн.: Философия науки. Естественнонаучные основы материализма. Ч. 1 (под ред. А. К. Тимирязева), вып. 2, 1924, с. 96.
⁶Там же, с. 104.
⁷Clifford W. Mathematical Papers. London, 1882, p. 21.
⁸Уилер Дж. А. Предвидение Эйнштейна. М., «Мир», 1970, с. 21.
⁹Neumann C. Über die Principien der Galilei—Newton’schen Theorie. Leipzig, 1870.
¹⁰Thomson W., Tait P. Treatise on Natural Philosophy. Vol. 1. Cambridge, 1890, p. 241.
¹¹Streintz H. Die physikalischen Grundlagen der Mechanik. Leipzig, 1883, SS. 24—25.
¹²Lange L. Die geschichtliche Entwicklung der Bewegungsbegriffes. Leipzig, 1886, S. 140.
¹³Мах Э. Механика. СПб., 1909, с. 198—199.
¹⁴Там же, с. 193
¹⁵Мах Э. Анализ ощущений и отношение физического к психическому. М., 1908, с. 283
¹⁶Мах Э. Механика, с. 427.
¹⁷Рlаnсk М. Zur Machschen Theorie der physikalischen Erkenntnis. Phys. Zeitschr., 1910, В 9. 11, S. 118.
¹⁸В настоящее время эти идеи Маха (известные как принципы Маха) живо обсуждаются в теории гравитации и общей теории относительности.

<<Назад Вперёд>>

Просмотров: 5669

загрузка...

Другие книги по данной тематике