§ 24. Механика Даламбера и Лагранжа
Следующее направление в развитии аналитической механики началось с появлением принципа сведения задач на движение к задачам на равновесие. Первый шаг был сделан Якобом Бернулли (1654—1705) в конце XVII—начале XVIII в. Неудовлетворенный теорией физического маятника Гюйгенса, основанной на применении закона сохранения энергии, Бернулли ищет другой метод решения задачи колебаний физического маятника. В основу своего метода он и положил принцип сведения задач на движение к задачам на равновесие. Чтобы иметь представление о теории Бернулли, рассмотрим маятник, образованный невесомым стержнем ОА, который может вращаться вокруг закрепленного конца О, нагруженный массами m1 и m2 (рис. 40).
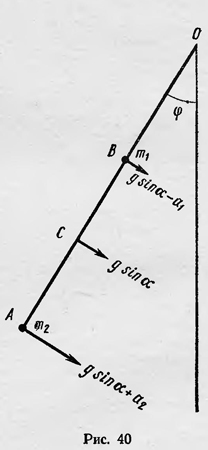
Каждая из масс стремится падать вниз с ускорением g. Из-за наличия стержня это стремление сводится к стремлению двигаться с ускорением g sinφ вдоль соответствующих дуг окружностей. Однако в результате наличия (другой массы) масса mi тормозится и ее ускорение меньше на некоторую величину а1. Наоборот, ускорение массы m2 больше на некоторую величину а2. Очевидно, что на стержне имеется точка С, ускорение которой равно g sinφ. Эта точка колеблется, как простой математический маятник, длина которого ОС=l. Эта точка называется центром качания. Задача заключается в / том, чтобы найти ее положение на маятнике. Ускорение массы mi равно g sinφr1/l, масса m2 имеет ускорение g sinφr2/l, где r1 = OB, а r2=ОА Таким образом, наличие связи приводит к тому, что масса mi теряет «побуждение» к движению на величину mi g sinφ(l-r1/l), а масса m2 приобретает дополнительно «побуждение» к движению, равное m2 g sinφ(r2/l-l). Основное предположение Бернулли состоит в том, что эти «побуждения» должны находиться в равновесии на рычаге, образованном массами m1 и m2 и невесомым стержнем ОА (рычаг второго рода). Это условие дает: 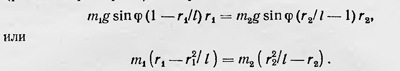
Отсюда для приведенной длины данного физического маятника получаем выражение 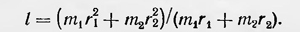
Несколько иначе принцип сведения задач на движение к задачам на равновесие применил в 1716 г. Герман в курсе механики «Форономия»1. Чтобы получить представление о способе применения этого принципа, разработанном Германом, рассмотрим физический маятник, который образован из ряда математических маятников, состоящих из невесомых стержней Оа1, Оа2, Оа3,..., нагруженных массами m1, m2, m3,... и имеющих общую ось вращения, которая проходит через точку О (рис. 41). Пусть эти простые маятники твердо связаны друг с другом, так что они образуют один физический маятник, центр качания которого и нужно найти. Маятник колеблется вследствие того, что к массам приложены внешние силы — силы тяжести Р1, Р2, Р3,..., равные соответственно m1g1, m2g2, m3g3,.... Однако из-за наличия связей массы двигаются так, как будто к ним приложены только «движущие силы» F1, F2, F3... ..., равные m1а1, m2а2, m3а3, ..., где а1, а2, а3,...— ускорения этих масс. Очевидно, что если к силам тяжести Р1, Р2, Р3 ... прибавить силы F1, F2, F3, ..., взятые с обратными знаками (т. е. силы инерции), то система будет находиться в равновесии. Таким образом, данная задача приводится к задаче равновесия двух систем сил: Р1, Р2, Р3, ... и —F1, —F2, —F3, ..., приложенных к нашей системе. 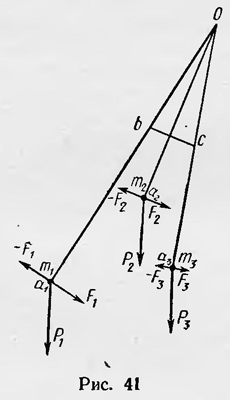
Герман полагает, что «побуждения» тяжести заменяются в результате наличия связей системой «побуждений», которые воспринимаются массами. Эти две системы «побуждений» Герман называет эквивалентными, и если «побуждения» связей направить в противоположные стороны, то они вместе с «побуждениями» тяжестей должны приводить систему в равновесие. Способ применения принципа сведения задач динамики к задачам статики, разработанный Германом, затем обобщил Эйлер, применивший его в 1740 г. к решению ряда задач динамики. Формулировка общего принципа Германа — Эйлера совпадает с формулировкой принципа, который в дальнейшем стали называть принципом Даламбера. Согласно последнему механические системы находятся в равновесии, если к действующим силам добавить силы инерции. 
Жан Даламбер В 1743 г. французский математик, физик и философ Жан Даламбер (1717—1783) напечатал книгу «Динамика», в которой предложил несколько иной принцип сведения задач динамики к задачам статики. Даламбер сыграл важную роль в развитии науки и философии в предреволюционной Франции. Ему принадлежат работы по различным вопросам физико-математических наук. Вместе с Дидро Даламбер был издателем и редактором первых томов знаменитой французской энциклопедии, в которых им написан ряд статей, в том числе и вводная. Основным понятием динамики Даламбер считал понятие движения. Он отрицательно относился к системе механики Ньютона, основанной на принципе ускоряющих сил. Даламбер говорил, что он «опирается только на расплывчатое и неясное положение, что действие пропорционально своей причине...», он «в механике бесполезен, и потому он должен быть из нее исключен»2. Понятие силы должно быть вообще исключено из механики, где следует основываться только на понятии движения. «Читатель не должен удивляться, — говорит Даламбер, — если я, исходя из этих соображений, так сказать, игнорирую «движущие причины» и рассматриваю исключительно движение, которое производится ими»3. Даламбер отмечает, что слово «сила» он будет употреблять исключительно для простого обозначения произведения массы на элемент ее скорости (т. е. приращения скорости или дифференциала скорости); «под ускоряющей же силой мы будем понимать просто элемент скорости»4. Поэтому Даламбер не считал второй закон Ньютона основным законом механики. В основе механики, по его мнению, лежат три основных положения: закон инерции, закон сложения движений и принцип равновесия. 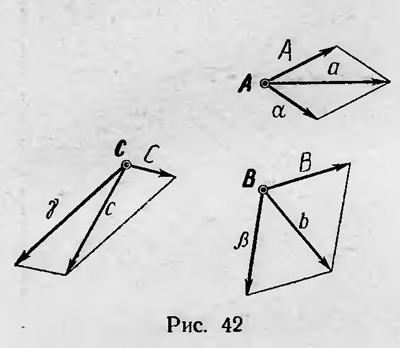
Для решения конкретных задач механики Даламбер предлагает принцип, позволяющий свести задачи на движение к задачам на равновесие. Он заключается в следующем. Рассмотрим систему тел А, В, С..... подверженных связям (рис. 42). Пусть этим телам сообщаются движения а, Ь, с, ... (Даламбер не употреблял понятие силы, поэтому, когда мы говорим, что к телу приложена сила, он писал, что телу сообщается движение. О сообщенных телу движениях Даламбер говорит и тогда, когда тело остается в покое. В этом случае сообщенные движения уничтожают друг друга). Сообщенные телам движения вследствие наличия связей не воспринимаются полностью преобразуются в движения А, В, С, ..., которые действительно приобретают эти тела. В результате этого сообщаемые движения можно представить состоящими из воспринятых движений А, В, С, ... и потерянных (или уничтоженных связями) движений α, β, γ, так что а=А +α, Ь=В +β, с=С+γ, ... . Последние движения должны быть таковы, чтобы система рассматриваемых тел со связями, получив их, оставалась бы в равновесии, т. е. движения α= а—А, β=b—B, γ=с—С,... уравновешивали бы друг друга, будучи сообщены системе данных тел. Таким образом, из приведенных рассуждений следует правило: «Нужно движения а, Ь, с, и т. д., передаваемые этим телам, разложить каждое на два движения: А и α, В и β, С и γ и т. д., причем эти последние движения должны быть таковы, что если телам будут переданы лишь движения А, В, С и т. д., то тела могут сохранить эти движения, не мешая друг другу; если же телам будут переданы лишь движения α, β, γ и т. д., то тела будут оставаться в покое»5. Поясняя этот принцип, Даламбер писал в другом месте: «...чтобы найти движение нескольких тел, действующих друг на друга, нужно разложить полученные телами движения... на два других движения. Эти составляющие движения должны быть подобраны таким образом, что у каждого тела одно из этих составляющих движений должно уничтожиться, а другое должно быть таким и так направленным, чтобы действие окружающих тел не могло ничего в нем изменить. Отсюда легко видеть, что все законы движения тел могут быть сведены к законам равновесия. В самом деле, для решения любой задачи динамики нужно только разложить движение каждого тела на два движения. Зная одно из этих составляющих движений, мы можем найти другое... Указанные условия всегда дадут все уравнения. Нет такой задачи динамики, которую нельзя было бы решить этим приемом или, по крайней мере, привести ее к уравнению, — а это есть все, что можно требовать от динамики. Мне кажется, что данное правило в самом деле приводит все задачи, относящиеся к движению тел, к более простой задаче, к задаче равновесия. Кроме того, этот принцип не опирается ни на какой вредный или неясный метафизический принцип. Он рассматривает в движении лишь то, что в нем в действительности имеется, т. е. пройденный путь и затраченное на это время. Он не пользуется ни действиями, ни силами, — одним словом, никаким из тех вторичных начал, которые, может быть, сами по себе и хороши и могут быть иногда полезными для сокращения и облегчения решения, «о которые никогда не будут началами первичными, поскольку метафизика этих начал никогда не станет ясной»6. Принцип, предложенный Даламбером, получил название «принципа потерянных сил». Как мы видим, формулировка его отличается от формулировки принципа, который в настоящее время называется принципом Даламбера. Современная формулировка принципа Даламбера больше похожа на принцип Германа — Эйлера, объединенный с принципом возможных перемещений. Современную форму этому принципу придал Лагранж. В своей «Динамике» Даламбер, руководствуясь установленным им принципом, решает задачи движения систем тел со связями, многие из которых в то время считались труднейшими. Однако при этом он не использует какой-либо единый аналитический метод. Приведя задачи динамики к задачам статики, он решал последние с помощью различных методов. 
Жозеф Луи Лагранж Дальнейшее развитие рассматриваемое направление в механике получило в трудах французского ученого Жозефа Лагранжа (1736—1813). Его труд «Аналитическая механика» вышел в свет в 1788 г. Лагранж ставил перед собой цель разработать такой аппарат механики, который давал бы возможность привести решение любой механической задачи к решению дифференциальных уравнений. «Я поставил себе целью, — писал Лагранж, — свести теорию механики и методы решения связанных с нею задач к общим формулам, простое развитие которых дает все уравнения, необходимые для решения каждой задачи. Я надеюсь, что способ, каким я постарался этого достичь, не оставит желать чего-либо лучшего»7. «В этой работе,— пишет далее Лагранж,— совершенно отсутствуют какие бы то ни было чертежи. Излагаемые мною методы не требуют ни построений, ни геометрических или механических рассуждений; они требуют только алгебраических операций, подчиненных планомерному и однообразному ходу. Все любящие анализ с удовольствием убедятся в том, что механика становится новой отраслью анализа, и будут мне благодарны за то, что этим путем я расширил область его применения»8. Лагранж блестяще решил данную задачу. Он разработал общий метод решения задач механики, позволяющий без каких-либо искусственных приемов приводить решение этих задач к решению дифференциальных уравнений. Лагранж разделял в своей книге статику и динамику, излагая их последовательно. В основу статики он кладет принцип возможных перемещений, который зародился еще в древности. В частных случаях в элементарном виде этот принцип применялся в XVII в. Впервые общую формулировку этого принципа привел Иоганн Бернулли. В одном из писем, относящихся к 1717 г., он писал: «Тело, на которое действуют любые силы, находится в равновесии, если сумма положительных энергий равна сумме отрицательных энергий. При этом под энергией понимается произведение силы на проекцию перемещения на направление силы. Это произведение имеет положительный знак, если направление проекции совпадает с направлением действия силы, и отрицательный знак, если они противоположны»9. Лагранж формулирует принцип возможных перемещений в виде принципа виртуальных скоростей. Он пишет: «Если какая-либо система любого числа тел или точек, на каждую из которых действуют любые силы, находится в равновесии и если этой системе сообщить любое малое движение, в результате которою каждая точка пройдет бесконечно малый путь, представляющий ее виртуальную скорость, то сумма сил, помноженных каждая соответственно на путь, проходимый по направлению силы точкой, к которой она приложена, будет всегда равна нулю, если малые пути, проходимые в направлении сил, считать положительными»10. Этот принцип Лагранж записывает в виде математического выражения Pdp + Qdq + Rdr + ... = 0. Здесь P, Q, R,... — приложенные к механической системе силы, а dp, dq, dr... — возможные перемещения этой системы в направлении соответствующих сил. Это выражение Лагранж называет «общей формулой статики» и формулирует ее кратко так: «сумма моментов всех сил равна нулю», понимая под словом «момент» работу соответствующей силы при возможном перемещении. Лагранж разрабатывает математический аппарат для применения принципа возможных перемещений в случае системы тел со связями, в частности он применяет разработанный им метод неопределенных множителей. В основу динамики Лагранж кладет принцип сведения задач динамики к задачам статики в форме Германа — Эйлера, рассматривая его как принцип равновесия между действующими силами и, говоря современным языком, силами инерции. «Этот способ сведения законов динамики к законам статики, — пишет Лагранж, — в действительности является менее прямым, чем способ, вытекающий из принципа Даламбера, но зато он приводит к большей простоте в применениях; он определяет собой возврат к методу Германа — Эйлера, который применил его при разрешении многих проблем механики. В некоторых курсах механики его можно встретить под названием принципа Даламбера»11. После сведения задачи динамики к задаче статики к последней можно применить принцип возможных перемещений и, таким образом, привести механическую задачу к задаче математической. Пусть имеется система материальных точек, каждая из которых имеет массу и занимает положение, определяемое значениями трех прямоугольных координат: хi, уi, zi. Пусть, далее, на каждую из этих точек действуют внешние силы Р, Q, (ускоряющие силы), под действием которых точки приобретают соответственно ускорения 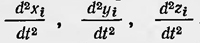 . Тогда тела под действием внешних сил и сил . Тогда тела под действием внешних сил и сил 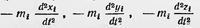 должны находиться в равновесии. Следовательно, должно выполняться условие должны находиться в равновесии. Следовательно, должно выполняться условие
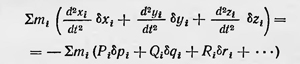
(величины Р, Q, по Лагранжу, не просто внешние силы, а «ускоряющие силы», т. е. силы, отнесенные к единице массы, поэтому в правой части равенства появляются множители кроме того, Лагранж считает σр, σq, σr положительными, когда их направление противоположно направлению действующих сил, отсюда и следует знак минус перед второй суммой). Полученное выражение Лагранж называет «общей формулой динамики»12. Для применения этой формулы к системе тел со связями Лагранж разрабатывает аналитический аппарат. Первый способ применения формулы, основанный на использовании метода неопределенных множителей, приводит к уравнениям Лагранжа первого рода. Второй, гораздо более интересный метод приводит к уравнениям Лагранжа второго рода, или просто уравнениям Лагранжа. Вводя обобщенные координаты, Лагранж путем замены переменных выводит из общей формулы динамики уравнения, которые для случая консервативной системы в современном виде таковы: 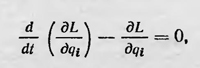
где qi — обобщенные координаты; Т — живая сила, выраженная в этих координатах; U — функция координат, определяемая, по Лагранжу, условием dU = Σmi(Pdp+Qdq + ...), т. е. функция, которая позже получила название потенциальной энергии. Эти уравнения в настоящее время, как известно, записывают в виде 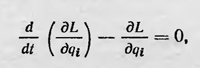
где L = T—U — функция Лагранжа, или лагранжиан. 1Герман — выдающийся математик, один из первых академиков Петербургской Академии наук. 2Даламбер Ж. Динамика, с. 21. 3Там же, с. 24. 4Там же, с. 59. 5Даламбер Ж. Динамика, с. 109. 6Даламбер Ж. Динамика, с. 354—355. 7Лагранж Ж. Аналитическая механика. Т. I, с. 9. 8Лагранж Ж. Аналитическая механика. Т. I, с. 9—10. 9Норре Е. Geschichte der Physik. Braunschweig, 1926, s. 65. 10Лагранж Ж. Аналитическая механика. Т. I, с. 42. 11Лагранж Ж. Аналитическая механика. Т. I, с. 313. 12Эту «фомулу» в современном написании обычно называют принципом Даламбера |
загрузка...
