§ 25. Развитие вариационных принципов механики
|
Рассмотрим, наконец, направление в развитии механики, основанное на сведении задач механики к решению вариационных задач. Идея о возможности применения вариационных принципов в механике пришла из оптики. В оптике же зародыш этой идеи появились еще в древности. Уже у Герона Александрийского встречается нечто подобное принципу Ферма для случая отражения света:
«Если природа не напрасно поработала над нашим зрением, то наш взглнд ломается под равными углами»1. Позже эту же идею со ссылкой на Герона повторяет древний ученый Дамиан: «В книге о зеркалах механик Герон показал, что прямолинейный путь света, ломающийся под равными углами, короче всех других, исходящих нз тех же (или) сходных частей и ломающихся в тех же частях под неравными углами»2. Следует отметить, что и Герон, и Дамиан полагали, что глаз наблюдателя испускает лучи, которые, как щупальца, ощупывают наблюдаемый предмет. Световой луч является как бы органом человека, и закон прямолинейного распространения света, как и закон отражения, имеет оттенок целесообразности, присущей деятельности живого организма. Вновь вопрос об экстремальности законов природы был поднят в связи со спором между Декартом и Ферма по поводу закона преломления света. Декарт объяснял закон преломления света, опираясь на гипотезу о том, что в оптически более плотной среде скорость света больше, нежели в оптически менее плотной. Французский математик Пьер Ферма (1601—1665) считал, что эта гипотеза противоречит здравому смыслу. Он сделал обратное предположение и пришел к заключению, что закон преломления можно получить, опираясь на принцип, подобный принципу Герона. В работе «Синтез для рефракции» (1662) Ферма так формулировал этот принцип: «Природа действует наиболее легкими и доступными путями»3. В 1696 г. Иоганн Бернулли, используя принцип Ферма, рассмотрел задачу о распространении луча света в среде с непрерывно меняющимся показателем преломления. Одновременно он показал, что математически эта задача не отличается от соответствующей задачи определения траектории движения материальной точки в поле сил. При этом он решил конкретную задачу о Брахистохроне, т. е. нашел кривую наибыстрейшего падения материальной точки в поле силы тяжести. Таким образом, для решения механической задачи был впервые применен метод вариационных принципов и впервые была отмечена аналогия между механикой и оптикой. По поводу этой аналогии Бернулли писал: «Я укажу, что можно открыть удивительное совпадение между кривизной луча света в непрерывно изменяющейся среде и брахистохронной кривой»4. С работы Бернулли, собственно говоря, и начинается история развития вариационных принципов механики. Начиная с 1744 г. французский ученый Пьер Мопертюи (1698— 1759) выступает со статьями, в которых утверждает, что он открыл новый всеобщий принцип, или закон природы, который он назвал принципом «наименьшего количества действия». Зная о работе Ферма по оптике, а также разделяя мнение, что свет в оптически более плотной среде распространяется с большей скоростью, нежели в среде, обладающей меньшей оптической плотностью, он не мог признать справедливость принципа Ферма. Тем не менее сама идея о том, что в природе действует вариационный закон, пришлась ему по душе. Будучи человеком религиозным, склонным к теологии, он усматривал в таком законе целесообразность устройства природы верховным существом. Он пришел к заключению, что в природе действует закон наименьшего действия. Действие, по Мопертюи, равно произведению массы на скорость и на пройденный путь. «Когда в природе происходит некоторое изменение, — писал Мопертюи, — Количество Действия, необходимое для этого изменения, является наименьшим возможным»5. Этот принцип, полагал Мопертюи, является всеобщим. Он действует во всех явлениях природы и прежде всего в механике. Сформулировав в общей форме всеобщий закон, Мопертюи пытался применить его в механике, а именно к случаям равновесия рычага и соударения тел. Однако, хотя он и получил правильные результаты, которые, вообще говоря, были заранее известны, тем не менее его рассуждения были далеки от ясности. Туманные рассуждения Мопертюи, обращение его к теологии вызвали возражения со стороны ряда ученых. Между ними и сторонниками Мопертюи разгорелся жаркий спор. К научной дискуссии примешивались и ненаучные сображения. В частности, Мопертюи обвинили в плагиате. Было опубликовано неизвестное письмо, якобы принадлежащее Лейбницу, в котором высказывалась идея о существовании вариационного физического принципа. В спор вступил Вольтер, который написал злой памфлет на Мопертюи под названием «История доктора Акакия и уроженца Сан-Мало». К тому времени Мопертюи был президентом Берлинской Академии наук. За него вступились академия и прусский король, который приказал уничтожить экземпляры сочинения Вольтера. Тем не менее, по словам Пекарского, Мопертюи «сделался посмешищем всей Европы»6. Одним из защитников Мопертюи был Эйлер, который в это время жил в Берлине и был членом Берлинской Академии наук. Эйлер считал, что Мопертюи действительно открыл новый всеобщий закон природы в самой общей форме. Эйлер независимо от Мопертюи установил принцип наименьшего действия для простых случаев движения материальной точки, причем в правильной математической формулировке. В 1744 г. в сочинении, посвященном началам вариационного исчисления, он показал, что задачу движения материальной точки в поле центральных сил можно свести к нахождению экстремума интеграла ∫vds, где v — скорость точки, а интеграл берется по всей траектории ее движения. Эйлер, как и Мопертюи, видел в применяемом принципе, так сказать, «экономическое усмотрение творца». Он писал: «Так как устройство всего мира — наиболее совершенное и так как оно исходит от мудрейшего Творца, то ничего не происходит в мире, из чего не вытекало бы ясно какое-нибудь свойство максимума или минимума; поэтому не может быть сомнения в том, что все действия в мире могут быть методом максимума и минимума выведены из целей, как и из самих действующих причин»7. Новый шаг в развитии вариационных принципов механики был сделан Лагранжем. Лагранж показал, что для действительных движений системы материальных тел, находящихся под действием центральных сил, интеграл ∫∑mividsi имеет экстремальное значение, т. е. σ∫∑mividsi=0 Вариация интеграла берется так, что общая энергия системы при этом не варьируется и все время выполняется теорема живых сил. Принцип наименьшего действия можно выразить иначе, если учесть, что ds = vdt, и ввести величину живой силы, а именно ∫∑Tdt = 0. В такой форме Лагранж называет этот принцип также «принципом наибольшей или наименьшей живой силы». Он уже не придает никакого метафизического смысла принципу наименьшего действия. Лагранж рассматривает его как одну из теорем механики, вытекающих из его общей «формулы динамики». Дальнейшее развитие вариационных принципов в механике связано с именем ирландского математика Вильяма Гамильтона (1805—1865), первоначально занимавшегося исследованием оптических явлений. Работы Гамильтона по оптике относятся к концу 20-х и началу 30-х годов XIX столетия. Это было время, когда хотя и начала уже торжествовать волновая теория света, однако оставались и сторонники корпускулярной теории света. Еще существовало мнение, что и та, и другая теория несовершенны, что в одних случаях волновая теория света лучше объясняет наблюдаемые явления, в других же случаях, наоборот, следует применять корпускулярную теорию света. Подобной точки зрения придерживался Гамильтон. При этом он считал, что вопрос о природе света не является существенным, и пытался создать математический аппарат, который мог быть интерпретирован как с волновой, так и с корпускулярной точки зрения для решения проблем оптики. Такой математический аппарат Гамильтон и разработал для геометрической оптики. В его основу Гамильтон положил принцип Ферма. Согласно пэтому принципу, для действительного пути светового луча между точками А и В интеграл 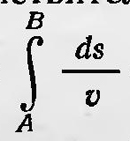 , где v — скорость света, должен иметь экстремальное значение. То же самое условие можно записать в виде , где v — скорость света, должен иметь экстремальное значение. То же самое условие можно записать в виде 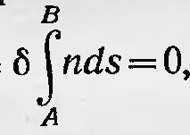 , где n — показатель преломления. Записанный выше интеграл можно рассматривать как функцию начальной А(х0; у0; z0) и конечной В(х; у; х;) точек, т. е. , где n — показатель преломления. Записанный выше интеграл можно рассматривать как функцию начальной А(х0; у0; z0) и конечной В(х; у; х;) точек, т. е. 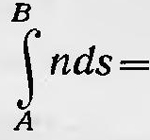 V(х0, у0, z0, х, у, х). Функцию V Гамильтон назвал характеристической. Если функцию V рассматривать как функцию только х, у, z, то, принимая во внимание принцип Ферма, получаем уравнение V(х0, у0, z0, х, у, х). Функцию V Гамильтон назвал характеристической. Если функцию V рассматривать как функцию только х, у, z, то, принимая во внимание принцип Ферма, получаем уравнение
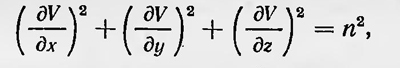
которому должна удовлетворять эта функция и которое впоследствии получило название уравнения Эйконала. Решая это уравнение, находим решение оптической задачи, которое можно интерпретировать с точки зрения как корпускулярной теории света, так и волновой теории (в геометрическом приближении). Зная функцию V (х, у, ), можно определить направляющие косинусы светового луча, которые соответственно равны: 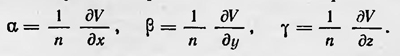
Знание же последних дает возможность построить траекторию луча в среде, т. е. решить оптическую задачу с точки зрения корпускулярной теории света. Решение оптической задачи можно, однако, интерпретировать и с позиций волновой теории света. Уравнение V (х, у, z) =const можно рассматривать как уравнение поверхности, которая является волновой. Учитывая далее, что 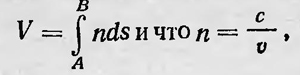 где с — скорость света в пустоте, получаем где с — скорость света в пустоте, получаем
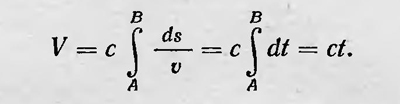
Отсюда следует, что волновая поверхность V (х, у, z) с течением времени перемещается в пространстве со скоростью, равной скорости света в данной точке среды. Действительно, dV=nds и dV= = cdt, откуда следует, что скорость распространения волновой поверхности ds/dt=v. Аналитический аппарат оптики Гамильтон переносит, в механику и разрабатывает новые общие принципы аналитической механики. Не рассматривая ход рассуждений Гамильтона, укажем лишь основные, наиболее важные результаты его исследований. Гамильтон рассматривал динамику системы тел, между которыми действуют центральные силы. В этом случае, как показал он, решение механической задачи сводится к нахождению некоторой функции 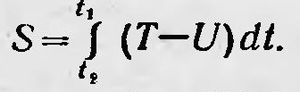 . Эту функцию Гамильтон называет главной. В настоящее время ее, как известно, называют также действием или действием по Гамильтону в отличие от функции . Эту функцию Гамильтон называет главной. В настоящее время ее, как известно, называют также действием или действием по Гамильтону в отличие от функции 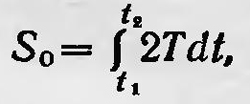 которую называют действием по Лагранжу или, иногда, укороченным действием. Здесь Т — кинетическая, a U — потенциальная энергия системы. Как и в оптике, для этой функции можно сформулировать вариационный принцип, а именно: которую называют действием по Лагранжу или, иногда, укороченным действием. Здесь Т — кинетическая, a U — потенциальная энергия системы. Как и в оптике, для этой функции можно сформулировать вариационный принцип, а именно:
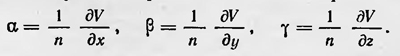
при постоянстве начальных и конечных значений координат и времени. Это и есть известный вариационный принцип, который в отличие от принципа наименьшего действия Мопертюи называют принципом стационарного действия или принципом наименьшего действия в форме Гамильтона. Если вычислить вариацию данного интеграла, то получим уравнения механики в форме Лагранжа. Функция S, подобно функции V в оптике, также является функцией начальных и конечных координат, а, также функцией времени: S=S (х0, у0, z0, х, у, z, t). Как и в оптике, эта функция удовлетворяет дифференциальному уравнению, которое подобно уравнению Эйконала в оптике. Это уравнение в настоящее время называют уравнением Гамильтона — Якоби: 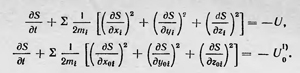 8 8
Здесь приведены два уравнения, как это делал сам Гамильтон. Немецкий математик Якоби показал, что для решения механической задачи достаточно одного уравнения от переменных х, у, z. В современных обозначениях уравнение Гамильтона или Гамильтона — Якоби имеет вид 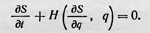
Решая данное уравнение, определим функцию S, зная которую получаем решение механической задачи. Гамильтон показал, что решение механической задачи систем тел, между которыми действуют центральные силы, сводится также к решению системы дифференциальных уравнений первого порядка (получивших название уравнений Гамильтона или канонических уравнений), которые в современном виде таковы: 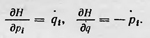
Аналитический аппарат механики, разработанный Гамильтоном, был обобщен и развит в трудах Якоби и русского математика Михаила Васильевича Остроградского (1801—1861), а затем в трудах других ученых. Помимо вариационных принципов (принципа наименьшего действия в форме Мопертюи и принципа наименьшего действия в форме Гамильтона) были предложены и другие вариационные принципы механики. Так, например, уже в 1829 г. Гаусс установил новый вариационный принцип механики — принцип наименьшего принуждения. Более общий принцип, который является в известном смысле его обобщением, установил Герц. В конце XIX в. вариационные принципы выходят за рамки механики и приобретают более широкий смысл. Гельмгольц взял за основу вариационный принцип наименьшего действия в форме Гамильтона и показал, что при надлежащем выборе лагранжиана, который он назвал кинетическим потенциалом, этот принцип применим не только в механике, но и в электродинамике, и некоторых других областях физической науки. В работе «О физическом значении принципа наименьшего действия», опубликованной в 1886 г., Гельмгольц писал: «Уже теперь можно считать вероятным, что этот принцип является общим законом для всех обратимых естественных процессов»9. Таким образом, начиная с конца XIX в принцип наименьшего действия играет в физике все большую и большую роль как общефизический принцип. Выявляется, что с его помощью можно просто и изящно сформулировать в математической форме основные законы многих общих физических теорий. Для этого нужно только определить переменные, которые следует взять за основу этой теории, и найти выражение соответствующего кинетического потенциала, или лагранжиана. Тогда одно уравнение, выражающее вариационный принцип, заменит множество математических соотношений данной теории. Открытие теории относительности еще больше укрепило значение принципа наименьшего действия, так как оказалось, что действие является релятивистским инвариантом. Вместе с этим и формулировка основных математических соотношений какой-либо физической теории с помощью принципа наименьшего действия также релятивистски инвариантна. Некоторые физики начинают рассматривать принцип наименьшего действия как один из самых фундаментальных принципов физики. Так, например, Планк считал этот принцип важнейшим физическим принципом, даже более важным, нежели принцип сохранения энергии. В статье «Принцип наименьшего действия», относящейся к 1915 г., он писал, что в достижении цели обобщения всех физических законов в неком едином принципе принцип наименьшего действия играет особую роль: «Среди более или менее общих законов, которые характеризуют достижения физической иауки в ее развитии за последние столетия, принцип наименьшего действия в настоящее время является как раз таким, который по форме и по содержанию может претендовать на то, что он ближе всего подошел к упомянутой выше идеальной конечной цели физического исследования. Значение принципа, если его выразить с необходимой общностью, распространяется не только иа механические, но также и на термические и электродинамические явления; во всех областях его применения он не только дает представление о некоторых свойствах встречающихся процессов, но совершенно отчетливо определяет ход физических процессов в пространстве и времени, отвечая на все относящиеся к этому вопросы, если известны необходимые постоянные и произвольно определяемые внешние условия»10. Правда, в конце статьи Планк вынужден заметить, что принцип наименьшего действия при всем его значении не может быть распространен на необратимое явление. Он пишет: «Правда, необратимость этот принцип никак не объясняет, так как в соответствии с ним каждый процесс может протекать как в пространстве, так и во времени в любом направлении — вперед или назад. Проблема необратимости поэтому здесь не подлежит обсуждению»11. Однако сейчас вариационные принципы применяют в физике еще в более широком масштабе; их используют и в термодинамике, и для описания необратимых процессов. В настоящее время вариационные принципы связывают с принципом симметрии, который сам по себе является одним из самых общих принципов науки. 1Ronki V. Storia dela luce Bologna, 1952, p. 23. 2Tам же. 3Вариационные принципы механики. — Сб. статей под редакцией Полака Л. С. М., Физматгиз, 1959, с. 7. 4Там же, с. 13. 5Там же, с. 53. 6Пекарский П. История Императорской Академии наук в Петербурге. Т. 1, СПб., 1870, с. 271. 7Мах Е. Механика. СПб., 1909, с. 383. 8Первоначально Гамильтон использовал вместо функция S функцию S*, называемую иногда укороченным действием, которая определяется соотношением 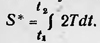 . Эта функция удовлетворяет уравнениям . Эта функция удовлетворяет уравнениям 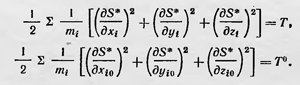
В данном случае аналогия с уравнением Эйконала еще более полная. 9Вариационные принципы механики, с. 433. 10Там же, с. 580. 11Вариационные принципы механики, с. 588. |
загрузка...
