§ 23. Законы сохранения в механике
|
Как уже отмечалось, первым был установлен закон сохранения количества движения. Он принадлежит Декарту, однако понимался им неверно. Вскоре ошибка Декарта была выяснена и этот закон стал общепризнанным. Его стали использовать при решении задач механики. В частности, он был применен для решения задачи об ударе тел.
Вторым был установлен в механике закон сохранения живых сил, или (в современном понимании) закон сохранения энергии. Этот закон был открыт не сразу. Как уже отмечалось, Гюйгенс, а еще раньше Галилей использовали частный случай закона сохранения энергии. Позже Лейбниц сформулировал уже в общей форме закон сохранения живых сил и противопоставил его закону сохранения количества движения. Он применял этот закон при решении конкретных задач механики. И Декарт, и Лейбниц исходили из общего положения, что движение в природе не может исчезать и возникать. Однако они по-разному устанавливали количественную меру движения. Если, по Декарту, мера движения — произведение массы на скорость, то Лейбниц считал, что движение измеряется его «силой», мерой же последней является произведение квадрата скорости на массу. Таким образом, получается, что движение, или его «сила» имеет две меры и соответственно имеют место два закона сохранения. Однако предположение о том, что движение может иметь две меры, многим показалось недопустимым; разгорелся спор о мере движения, или о «силе» движения. Одни ученые полагали, что мерой движения нужно считать произведение массы на скорость, т. е. следовали Декарту, другие, отстаивая точку зрения Лейбница, утверждали, что мерой движения, его «силой», является произведение массы на квадрат скорости. В 1743 г. французский ученый Даламбер называет этот спор пустым метафизическим спором о словах, не имеющих научного смысла. По Даламберу, и меру Декарта, и меру Лейбница с одинаковым успехом можно рассматривать в качестве меры движения, или «силы». Все зависит от того, какой смысл вкладывать в понятие «силы» движения. Вообще же, считает Даламбер, это понятие не играет в науке никакой роли. Нужно решить, говорит Даламбер, что понимать под силой движущегося тела и чем ее измерять. Если ее измерять «абсолютной величиной препятствий» (которая равна, по Даламберу, ΣFΔS, где F — сила, а ΔS—элемент пути), то прав Лейбниц. Если же ее измерять «суммой сопротивлений препятствию» (которая, по Даламберу, равна ΣFΔt или ΣΔmv), то правы картезианцы. Если помнить это, то никакой путаницы не возникнет и оба лагеря будут правы. Даламбер писал: «Поскольку в слове «сила» не содержится никакого ясного и точного смысла помимо соответствующего ей действия, я полагаю, что нужно каждому предоставить свободу решать данный вопрос по его усмотрению. К тому же затронутый вопрос представляет собой не более, как совершенно бесплодный метафизический спор о словах, недостойный внимания философов»1. Конечно, в рамках механики этот спор не мог быть решен. Учитывая последующее развитие физики, можно сказать, что прав был Лейбниц, гак как выяснилось, что механическое движение способно превращаться в другие виды движения в определенных количественных соотношениях, т. е. был установлен закон сохранения и превращения энергии. И механическая энергия определяется не произведением массы на скорость, а произведением массы на квадрат скорости. На это обстоятельство обратил внимание Энгельс, который дал полный анализ этого спора, уже опираясь на закон сохранения и превращения энергии2. Как уже говорилось, Лейбниц положил закон сохранения живых сил в основу механики и применял его для решения некоторых механических задач. В этом вопросе последователем Лейбница был Иоганн Бернулли (1667—1748). Критикуя Ньютона, который в «Оптике» выразил сомнение в сохранении движения в природе и говорил о необходимости поддерживать это движение активными началами, Бернулли писал: «... совершенно исчезает страх перед тем, что когда-нибудь в природе исчезнет движение и весь мир погрузится в страшный неподвижный хаос. Будем же спать спокойно, дело обстоит благополучно»3. 
Даниил Бернулли Защищая положение о сохранении живых сил в природе, И. Бернулли широко использовал это положение для решения механических задач. В 1723 г. он написал «Рассуждение о законах передачи движения». В этом сочинении он применил закон сохранения живых сил для упругого удара, успешно решив ряд задач об упругом ударе шаров, в том числе и нецентральном. В других трудах, также применяя этот закон, Бернулли решал другие задачи механики, в том числе задачу колебаний физического маятника, а также применил этот закон для исследования колебания струн. Широко использовал закон сохранения живых сил Даниил Бернулли (1700—1782). С помощью этого закона он вывел известное уравнение гидродинамики, носящее его имя. Бернулли рассмотрел вопрос о применимости закона сохранения живых сил для случая системы материальных точек, между которыми действуют центральные силы. В работе «Замечания об общем понимании закона сохранения живых сил» (1748) Бернулли доказал, что для системы материальных точек, которые находятся под действием сил притяжения, зависящих обратно пропорционально квадратам расстояния между ними, изменение живой силы этой системы зависит только от начальных и конечных положений точек и что если эти точки возвращаются в начальное положение, то живая сила принимает прежнее значение. Бернулли подчеркнул, что это положение справедливо и для случая центральных сил, действующих по любому закону. Он писал: «Общий закон (закон сохранения живых сил.— Б. С.) справедлив для любого гравитационного закона. Только с целью облегчения формул и уменьшения интегралов я ограничился законом обратной пропорциональности квадратам расстояния. Но природа никогда не отказывается от великого закона сохранения живых сил, это я и хотел показать4. Закон сохранения живых сил для общего случая системы материальных точек, находящихся под действием центральных сил, был затем получен Лагранжем и опубликован в 1788 I. в «Аналитической механике». Если Хi, уi и zi — координаты материальных точек системы, а mi — массы этих точек, то для данного случая справедливо соотношение 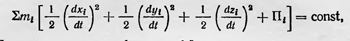
где Пi — потенциальная функция i-й частицы, отнесенная к единице массы (Лагранж этот термин не использовал). В отличие от своих предшественников Лагранж уже не придает принципиального значения закону сохранения живых сил и рассматривает его как следствие общих положений механики. Третий закон сохранения — закон сохранения момента количества движения — был установлен в 1746 г. почти одновременно Эйлером и Д. Бернулли при разработке теории вращательного движения. Согласно их формулировке, как указывает Лагранж, «...при движении нескольких тел вокруг неподвижного центра сумма произведений массы каждого тела на его скорость вращения вокруг центра и на расстояние его от того же центра является всегда независимой от взаимного действия, которое тела могут производить друг на друга, и должна всегда оставаться неизменной, если не имеется какого-либо внешнего действия или препятствия»5. Французский ученый Дарси в 1747 г. сформулировал закон сохранения момента количества движения для системы тел: сумма произведений масс тел на площади, описываемой радиуса-векторами, проведенными из любой точки к этим телам за определенный промежуток времени и спроектированными на любую плоскость, пропорциональна этому промежутку времени. В дальнейшем Дарси сформулировал этот закон как закон сохранения суммы произведений масс тел, их скоростей и перпендикуляров, опущенных из точки на направление движения. В такой формулировке этот закон Дарси назвал законом сохранения действия и, считая его общим принципом природы, противопоставил принципу наименьшего действия, высказанным к тому времени Мопертюи. Законы сохранения (закон сохранения живых сил, а также законы сохранения количества движения и момента количества движения) первоначально выдвигались как всеобщие законы природы, в последующем же были сведены до ранга следствий общих законов механики или принципов, следствий, не имеющих уже фундаментального, универсального значения. Однако по мере развития науки эти законы вновь приобрели принципиальное значение и получили окончательный смысл общих законов природы. Не говоря уже о законе сохранения энергии — одном из самых общих законов природы, законы сохранения количества и момента количества движения также являются общими законами физики, применимыми, как известно, и к немеханическим формам движения материи, например к электромагнитному полю. Наконец, в еще более позднее время рассмотренные законы сохранения (в связи с теоремой Неттер) приобрели смысл законов, выражающих общие свойства пространства и времени. 1Даламбер Ж. Динамика. М. — Л., Гостехиздат, 1950, с. 27. 2Энгельс Ф. Мера движения — работа. — Диалектика природы. (Маркс К., Энгельс Ф. Соч. Изд. 2-е. Т. 20, с. 408.) 3Бернулли И. Избранные сочинения по механике. М.— Л., Гостехиздат, 1937, с. 247. 4!> Abhandlungen iiber jene Grundsatze der Mechanik, die Integrate der Differen-tialgleichungen liefern von Isaak Newton, Daniel Bernulli und Patrick d’Arcy. Ostwald’s klassiker. Leipzig und Berlin, 1914, s. 74—75. 5Лагранж Ж. Аналитическая механика. Т. I, с. 317. |
загрузка...
