XIX. Мемуары «Воображаемая геометрия» и «Применение воображаемой геометрии к некоторым интегралам»

Мемуар «О началах геометрии», как уже сказано, содержал все основные идеи Лобачевского. В расцвете лет, в период с 1823 до 1832 г., Лобачевский создал свою новую геометрию и так ее разработал, что по существу ее содержания немного оставалось к этому прибавить. Но напряженные размышления, с нею связанные, не покидали ее творца.

Его творение не было признано, было осмеяно. Лобачевский тяжело это пережил, но обескуражен этим не был. Обвинения, выдвинутые против созданной им геометрии, по существу были лишены основания; нужно было их опровергнуть. Остроградский находил, что работа Лобачевского была выполнена с малым старанием. Это было неверно; но, как уже выяснено, справедливо было то, что мемуар «О началах геометрии» был изложен слишком сжато, непонятно, не был достаточно развит. Во введении к другому мемуару, к которому мы теперь обращаемся, Лобачевский говорит об этом следующее:

«В тесных пределах повременного сочинения не мог изложить я моего предмета со всей подробностью. Много предложений, помещенных без доказательства, одни выводы из продолжительных и довольно запутанных вычислений заставляют меня подозревать, что мое сочинение, казавшись с первого взгляда темным, предупреждало охоту заняться им с некоторым вниманием и даже могло подать повод усумниться в строгости моего суждения и в верности выведенных заключений».

Но были и размышления другого рода, еще более серьезные, сомнения, которые проистекали из существа предмета и которые в некоторой степени не были чужды и самому Лобачевскому.

В своем заключении, которым заканчивается работа «О началах геометрии», Лобачевский старается убедить читателя, что созданная им геометрия не содержит противоречий, что ни к какому противоречию не может привести никакое дальнейшее ее развитие. Доводами, подтверждавшими такое заключение, служили, с одной стороны, цельность и законченность основ новой геометрии, допускающей такое же неограниченное развитие, как и обыкновенная геометрия, а с другой стороны, постоянное совпадение результатов вычислений, которые различными способами выполняются средствами этой геометрии. И действительно, всякий, кто проштудирует мемуар «0 началах геометрии», убеждением этим несомненно проникнется. Но сколь бы сильным это убеждение ни было, оно остается субъективным; действительно объективного, вполне убедительного доказательства, как теперь обыкновенно говорят, «непротиворечивости» воображаемой геометрии, строгого доказательства того, что противоречие в этой геометрии не может появиться, как бы далеко мы ее ни развивали, — его в рассуждении Лобачевского, конечно, не было, и он сам хорошо эго понимал. «Эта причина, — признается Лобачевский в том же предисловии к «Воображаемой геометрии», — понудила меня искать другого способа увериться самому в истине мной показанного и потом осмелиться еще раз представить мои исследования на суд ученых».

В 1834 г. по инициативе Лобачевского начинают выходить «Ученые записки Казанского университета». Первая книга открывается краткой вступительной статьей Лобачевского, о которой нам придется говорить ниже; за этим, в первой книжке за 1835 г. следует мемуар «Воображаемая геометрия». Собственно, этот мемуар был раньше составлен на французском языке и послан в журнал Крелля; но в этом журнале он появился только через два года¹. Причина задержки — заключалась ли она в очередности поступавших в редакцию статей или были колебания относительно его печатания — остается невыясненной. Во всяком случае Лобачевский перевел эту работу на русский язык, внес при этом некоторые изменения и в таком виде опубликовал ее в «Ученых записках», а также выпустил отдельным изданием. В следующем, 1836 г. в тех же «Ученых записках» появился мемуар, представлявший продолжение «Воображаемой геометрии» и носивший название «Применение воображаемой геометрии к некоторым интегралам». Он был предварительно составлен на французском языке для журнала Крелля².

Обе работы составляют одно целое. По существу они представляют лишь развитие идей, содержащихся в мемуаре «О началах геометрии». Желая отпарировать возражения, основывающиеся на геометрической несообразности выводов, Лобачевский становится теперь на другой путь, как он сам говорит, до некоторой степени противоположный тому, которым он шел в первом мемуаре.

Рассуждение начинается следующими соображениями. Пусть а — произвольное положительное число, которое можно рассматривать как длину некоторого отрезка; пусть а' — функция от а, именно угол, который определяется уравнением

ctg 1/2а'=e^{a (37)

Ясно, что это та же функция, которую Лобачевский обозначал через F(a) или П(а) (см. формулу (14) (стр. 219) в предположении, что постоянная k = 1. Теперь Лобачевский становится на странную, на первый взгляд, позицию. Приводим снова его подлинные слова:

«В прямолинейном прямоугольном треугольнике пусть r — гипотенуза, р и q — катеты, Р и Q — противоположные им углы. В предположении Р + Q < d, допускаем и посмотрим, к каким заключениям поведут далее такие уравнения».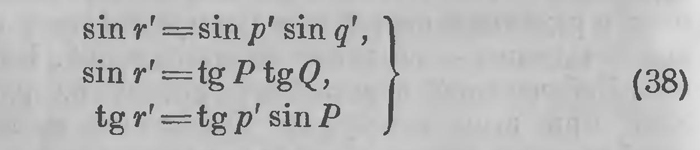

Лобачевский, таким образом, пишет уравнения прямоугольного треугольника в таком виде, как они должны иметь место в «воображаемой геометрии»; он ставит теперь себе целью показать, что возможна геометрия, в которой стороны и углы прямоугольного треугольника связаны этими наперед заданными уравнениями.

Титульный лист отдельного издания «Воображаемой геометрии».

Прежде всего Лобачевский доказывает, что из этих уравнений вытекает ряд других соотношений, именно те, которые в главе XV приведены под номерами (11а) — (11е). Из этих уравнений прямоугольного треугольника Лобачевский выводит соотношения, которые в силу сделанного предположения должны связывать стороны а, b, c и углы А, В, С любого треугольника. С большим искусством он выводит вслед за тем соотношение, которое — подчеркнем еще раз, в сделанных предположениях — определяет сумму углов S = А + В + С треугольника: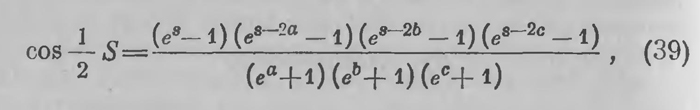

где s = а + b + с — периметр треугольника. Он устанавливает, далее, что правая часть есть положительное число, меньшее единицы, а следовательно сумма углов меньше двух прямых.

Теперь Лобачевский спрашивает, удовлетворяют ли уравнения, связывающие стороны и углы треугольника, выведенные в сделанных предположениях, тем условиям, при которых составление всякого треугольника возможно. «Таких условий, независимо от значения суммы трех углов, — говорит он дальше, — находится только два: составление треугольника всякий раз возможно, когда даны или три стороны, из которых сумма двух более третьей или две стороны и угол между ними произвольные».

Требование, чтобы сумма двух сторон всегда была больше третьей, теперь обыкновенно называется постулатом треугольника. Лобачевский дает утвердительный ответ на поставленный вопрос, основанный на следующих соображениях. Он показывает, что каковы бы ни были заданные две стороны и угол между ними, или три стороны, удовлетворяющие т. н. постулату треугольника, уравнения дают действительные значения остальных элементов треугольника; поэтому треугольник, имеющий заданные элементы, возможен.

Лобачевский показывает затем, так же как это было сделано в первом мемуаре, что уравнения треугольника сводятся к обычным уравнениям евклидовой геометрии, когда стороны треугольника весьма малы. Отсюда Лобачевский делает следующие выводы:

«1. В теории ничто не мешает сумму углов прямолинейного треугольника принимать менее двух прямых.

2. С таким предположением уравнения (13)³ заменяют уравнения (15)⁴ и не могут вести к ложным заключениям.

3. Воображаемая геометрия обнимает употребительную геометрию, как частный случай, к которому переходим, принимая линии бесконечно малыми: так что в этом отношении употребительная геометрия может быть названа Геометрия дифференциальная.

4. Значения для элементов линии, поверхности и объема тел в обеих геометриях одинаковы.

5. Предположение, что сумма углов треугольника менее двух прямых, может быть допущено только в применении к аналитике, потому что измерения в природе не открывают нам в этой сумме ни малейшего отклонения от половины окружности».

Можно ли считать эти соображения вполне убеди тельными? Конечно, нет. Не видно, что дает право на утверждение, содержащееся в основном положении 1. Верно то, что эти рассуждения пополняют те выводы, которые содержатся в мемуаре «О началах геометрии». Лобачевский чувствует себя на твердой почве с того момента, когда установлены основные тригонометрические уравнения (11а) — (11е). В мемуаре «О началах геометрии» установлено, что к этим уравнениям приводит постулат о параллельных в том виде, как он принят Лобачевским; в «Воображаемой геометрии» установлено обратное: из этих уравнений вытекает, что сумма углов треугольника меньше 2с?, а следовательно, вытекает и вся воображаемая геометрия. В этой постановке с особенной остротой стоит вопрос, что дает основание устанавливать a priori тригонометрические уравнения (38), совпадающие о прежними основными уравнениями (11а) — (11с). Этот вопрос тут же ставит и сам Лобачевский. «Может быть кому-нибудь покажется с первого взгляда предположение уравнений (1), (2), (3)⁵ столь произвольным, что его легко заменить другим; однакож этого сделать нельзя, как доказал я в моем сочинении «О началах геометрии». Лобачевский, таким образом, и сам стоит на том, что оба мемуара друг друга дополняют, но один другого не заменяет. И к сожалению, ни один из этих мемуаров не устанавливает твердо того основного факта, который так занимал Лобачевского, который действительно играет главную роль — не решает вопроса о непротиворечивости воображаемой геометрии. Нужно сказать, что Лобачевский был очень близок к решению этого вопроса. По существу, это решение у него собственно уже имеется; его нужно было иначе, точнее формулировать. Но это Лобачевским не было сделано; дать исчерпывающее решение вопроса составило уже удел его последователей.

По вопросу о том, какая же геометрия действительно имеет место в реальном пространстве, Лобачевский, как видно из положения 5, теперь склоняется в пользу геометрии Евклида; он мотивирует это результатами тех опытных данных, которые приведены в мемуаре «О началах геометрии». Он прибавляет к этому, что надо «вместе с тем быть убежден и в том, что независимо от опыта напрасно было бы искать доказательства на такую истину, которая еще не заключается в нашем понятии о телах».

Этим заканчивается первая часть мемуара — попытка с самого начала дать более убедительное доказательство того, что «воображаемая геометрия» не содержит в себе противоречий. Однако очень любопытные соображения, которые Лобачевский для этого приводит, все же нельзя считать вполне убедительными: Лобачевский и сам это понимал, как это видно из его высказываний, его исканий в других работах.

Вторую часть мемуара составляет вывод элементов длины, площади и объема; этот вывод мало чем отличается от того, который был дан в первом мемуаре.

Частью попутно, частью вслед за этим проводятся вычисления, имеющие своей основной задачей применение воображаемой геометрии к вычислению определенных интегралов. Основной замысел тот же: одна и та же геометрическая величина находится различными способами: либо путем расчленения на части, различным образом проводимого, либо интегральными вычислениями в различных координатах. В том и в другом случае сопоставление результатов приводит либо к установлению значения того или иного определенного интеграла, либо к преобразованию определенного интеграла в другой, более простой. Мемуар «Применения воображаемой геометрии к некоторым интегралам» заканчивается таблицей, содержащей 50 формул, которые выражают такого рода результаты. «Искусство, с которым Лобачевский выполняет отого рода преобразования, — замечает Либман, — вызывает удивление... это искусство носит печать гениальности». Вместе с тем, по словам того же Либмана, и эти мемуары больше, чем какая-либо другая из его работ, оправдывают замечание Гаусса, что работа Лобачевского напоминает непроходимый девственный лес. Как было указано выше (стр. 241), Либман выпустил немецкий перевод этих двух мемуаров с пояснительными комментариями. Он говорит в предисловии: «Не без большого труда, иногда только при помощи сильного специального приема, переводчику удалось произвести целесообразное разбиение материалов на части и выполнить вычисления. И здесь необходимо с определенностью сказать, что ему не везде удавалось проникнуть в цель, которую автор себе ставил». Значительное большинство вычислений посвящено разысканию объемов пирамид и прежде всего тетраэдров (трехгранных пирамид). И здесь автор развивает те же методы, которыми он пользовался в мемуаре «О началах геометрии». Этих методов собственно два. Один заключается в том, что пирамида разбивается на конические вырезки, дается выражение бесконечно малого вырезка, которое интегрируется по различным частям основания. Второй прием включается в том, что вычисляется объем конуса и пирамиды с бесконечно удаленной вершиной; это значит, что по отношению к конусу рассматривается случай, когда все образующие параллельны между собой (рис. 31); объем оказывается конечным, и вычисление его приводится к сравнительно простому интегралу. То же относится к пирамиде с параллельными боковыми ребрами (рис. 32). Когда найдены выражения для объема любой такой пирамиды, объем тетраэдра вычисляется как разность объемов таких предельных пирамид. Такое разбиение может быть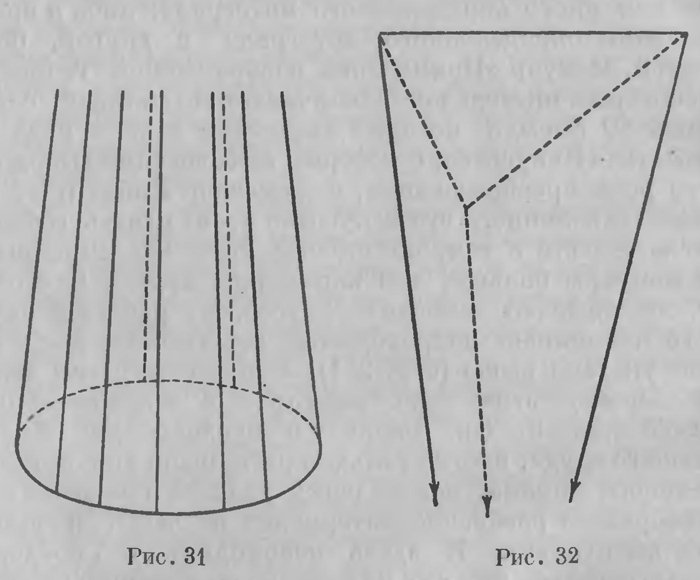

выполнено различными способами; это сопоставление вновь приводит к любопытным аналитическим результатам. Излагать здесь отдельные примеры таких результатов вряд ли целесообразно. Читателю, который этим интересуется, следует обратиться к подлинным работам Лобачевского, которые выпущены в настоящее время с обстоятельными комментариями. Здесь мы ограничимся только немногими указаниями.

Лобачевский имел в своем распоряжении сборник задач на вычисление определенных интегралов, составленный Лежандром⁶. Лобачевский получает значение ряда этих интегралов, два из которых он находит особенно удачно. Он находит ряд интегралов, по отношению к которым некоторые интегралы Лежандра составляют только частные случаи. Он получает значение определенного интеграла, которым занимался Лагранж, нашедший его значение только для частного случая. Вычисление объема пирамиды часто приводит к функции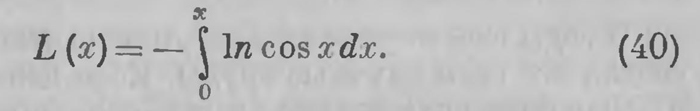

Преобразования же интегралов, которыми эти объемы выражаются, приводят к линейным соотношениям между значениями функции (40) для различных значений аргумента. При помощи функций (40) Лобачевский дает здесь общее выражение интеграла, который вызвал возражения Остроградского; оно содержится в формуле XXXIII его таблицы.

Нужно иметь в виду, что это было время, когда традиции Эйлера были очень сильны и формальные выводы ценились высоко. Лобачевский с удовлетворением констатирует, что ему удалось привести некоторые интегралы к эллиптическим интегралам того или иного рода или к функциям, которые просто развертываются в тригонометрические ряды. Эти результаты сохранили значение и по настоящее время. В современных справочниках по определенным интегралам имя Лобачевского встречается очень часто. Еще в 1858 г. Д. Биренс (D. Bierens de Haan) выпустил обширные таблицы определенных интегралов с подробными библиографическими указаниями. В эти таблицы вошли интегралы Лобачевского.

Все эти результаты весьма интересны сами по себе; они несомненно утверждают субъективную уверенность в полной логической правильности воображаемой геометрии, но объективного доказательства ее непротиворечивости они, конечно, не дают; самый этот метод к такому результату привести не может. Это сознание не покидало Лобачевского до конца его жизни.

¹N. I. Lobatschefskij. Geometrie imaginaire. Journal fur reine und angewandte Mathematik. 1837, Band 17.

²«Application de la g£om6trie imaginaire Si quelques integrates».

³Тригонометрические уравнения воображаемой геометрии

⁴Тригонометрические уравнения евклидовой геометрии.

⁵Т. е. трех основных уравнений (38) прямоугольного треугольника.

⁶А. М. Legendre. Exercises de calcul integral, I partie. 1’aris, 1811. К нему добавление в 50 страниц «Supplement & la pre-inifere partie», выпущено без указания даты. В нем дана таблица Table g6n6rale des formules. Этот первый сборник определенных интегралов до некоторой степени служит для Лобачевского образцом.}