Астрономия
|
В астрономии, как и в математике, два столетия, последовавшие за смертью Гиппарха, были весьма не плодотворным периодом, не выдвинувшим ни одного значительного имени. Нельзя, впрочем, сказать, что астрономией в это время перестали заниматься; наоборот, она продолжала оставаться одной из самых популярных наук. Мы знаем, что в это время энциклопедист Посидоний, не будучи астрономом-профессионалом, производил расчеты по определению сравнительных размеров Земли, Луны и Солнца и расстояний между ними, следуя в этом отношении Аристарху и Гиппарху.
В это же время процветали астрономы-популяризаторы, такие, как Гемин (I в. до н. э.) и Клеомед (I в. н. э.), в сохранившихся сочинениях которых можно найти многоценной историко-астрономической информации. Об интересе к астрономии в эту эпоху свидетельствует, в частности, широкая популярность дидактической поэмы Арата «Явлеция», о которой мы упоминали выше. Любопытно, что эту поэму перелагали на латинский язык такие лица, как Варрон, Цицерон и Цезарь Германик. Но имел ли место в это время хоть какой-либо прогресс в настоящей астрономической науке? На этот вопрос мы не можем ответить утвердительно. Новая информация, позволяющая думать, что астрономические изыскания не прекратились полностью, относится лишь к концу I в. п. э. В этот период — период стабилизации Римской империи — астрономическая наука начинает возрождаться. Но это была уже другая астрономия, существенным образом отличавшаяся от астрономии эпохи расцвета александрийской пауки. Отличительные черты этой поздней античной астрономии состояли в следующем. 1. Происходит окончательное усвоение достижений вавилонской астрономии. Это выражается не только в использовании данных вавилонских наблюдений, не только в усвоении шестидесятеричной системы счисления, но и в том, что в греческую науку проникают вычислительные методы вавилонян, основанные на операциях с. линейными числовыми разностями. Будучи значительно более "Примитивными по сравнению с геометрическими методами греков, эти числовые методы сосуществуют рядом с ними, с течением времени находя все более широкое применение. 2. Чистые струи астрономической науки, созданной трудами Евдокса, Аристарха и других гениев той эпохи загрязняются текущим с Востока мутным потоком астрологии. Особый успех астрология имеет у римлян, склонных ко всякого рода суевериям и предрассудкам. При этом астрология в греко-римском мире приобретает существенно иные функции по сравнению с той ролью, какую она играла в странах Древнего Востока. Там наблюдения за такими небесными явлениями, как затмения, появления комет, необычные сочетания планет, имели целью предугадать счастливые или, чаще, пагубные события, предвестием которых эти явления считались (победа или поражение в войне, голод, наводнение, засуха и т. д.). Теперь же движение небесных светил стало связываться с индивидуальными судьбами людей. Основной и, в сущности, единственной задачей астрологии становится составление гороскопов, причем этим делом вынуждены заниматься самые крупные ученые. Более того, интерес к астрологии был важнейшим фактором, обусловившим новый подъем астрономической науки. Выдающимся астрономом конца I в. н. э. был Менелай Александрийский, о котором мы уже писали в разделе математики. Имеются сообщения, что во время своего пребывания в Риме Менелай изучал покрытия звезд Луной. Аналогичные наблюдения производил примерно в то же время некий Агриппа в Вифинии. Эти наблюдения были использованы Птолемеем, который, сравнивая их с наблюдениями, полученными в свое время Тимохарисом и позже Гиппархом, а также со своими собственными данными, вычислил па их основании величину смещения равноденствия (прецессии). Показательным для характеристики астрономических представлений у образованных людей того времени был трактат Плутарха «О лике, видимом на диске Луны» (начало II в. н. э.). Луна описывалась Плутархом как тело, подобное Земле (хотя и меньшей величины), на котором имеются горы, отбрасывающие глубокие тени. Эти представления имели уже существенно иной характер по сравнению с воззрениями, господствовавшими в эпоху Платона и Аристотеля. Высшей точкой развития античной астрономии и одновременно ее последним крупным достижением следует считать основной труд Клавдия Птолемея «Математическая система» (по-гречески «Mathematike syntaxis»), получивший впоследствии известность под арабизированным названием «Альмагест». В этом сочинении Птолемей до конца осуществил программу Гиппарха, состоявшую в создании геоцентрической системы мира, в которой видимое движение Луны, Солнца и пяти планет объяснялось бы с помощью эксцентрических кругов и эпициклов. О жизни величайшего астронома древности мы ровно ничего не знаем — за исключением того, что первое наблюдение, включенное им в «Альмагест», было произведено в 125 г., а последнее — в 151 г. Все это время он жил и работал в Александрии; там же он, по-видимому, и умер (около 170 г.). Из астрономических сочинений Птолемея, кроме «Альмагеста», нам известны два: две книги «О планетах», в которых птолемеевская теория движения планет излагается в сокращенном виде, и книга о положениях звезд, содержащая таблицы восхода и захода звезд для пяти точек, находящихся на разных широтах от Черного моря до Сиены (Ассуапа). О его астрологическом сочинении «Тетрабиблос» будет сказано ниже. Для построения теории движения планет Птолемей должен был решить две задачи. 1. Определить движение центра эпицикла по эксцентрическому кругу (так называемому «деференту»); 2. Определить движение планеты по эпициклу. Для решения первой задачи нужно было наблюдать планету в те моменты времени, когда она лежит на прямой, соединяющей центр эпицикла с Землей. Согласно основному принципу теории эпициклов, радиус эпицикла, на конце которого находится планета, всегда направлен в ту же сторону, что и радиус солнечной орбиты, на конце которого находится Солнце. Сложность задачи состояла в том, что Полете предполагалось движущимся по круговой орбите не вокруг Земли, а вокруг эпицентра (рис. 15), поэтому момент, когда планета оказывалась как рае против центра эпицикла, не совпадал с моментом, когда она находилась в противостоянии с Солнцем. Все это требовало проведения очень большого числа наблюдений, которые Птолемей выполнил с помощью инструмента с градуированными кругами, названного им «астролябон» и описанного в пятой книге «Альмагеста». При этом выяснилась еще дополнительная трудность. Мы уже знаем, что центр эпицикла планеты должен описывать эксцентрический круг, центр которого находится вне Земли. И вот оказалось, что теория будет соответствовать наблюдениям только в том случае, когда движение центра эпицикла будет выглядеть равномерным не из центра его орбиты, а из другой точки — так называемого «экванта»,— расположенного на таком же расстоянии от центра орбиты, на каком, но только с другой стороны, находится от него Земля (рис. 16). Это означало, что фактически центр эпицикла движется по своей орбите не равномерно: в перигее, т. е. вдали от экванта, он движется быстрее, а в апогее (вблизи экванта) — медленнее. Следует заметить, что Птолемей вынужден был допустить наличие экванта также и для движения Луны. Он не объясняет, каким образом он пришел к идее экванта. Он только пишет: «...мы нашли, что...» 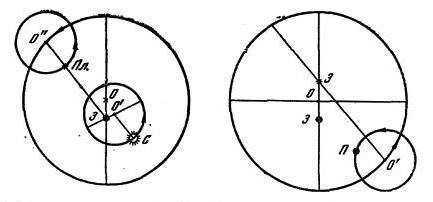
Рис. 15. Соотношение движения Солнца и планеты по Птолемею: С — Солнце, 3 — Земля, Пл — планета, О — центр деферента, О’ — центр солнечной орбиты, О’’ — центр эпицикла Рис. 16. Движение центра эпицикла О’ кажется равномерным, если наблюдать его не из центра деферента О, а из экванта Э Вторая из указанных выше задач состояла в определении размеров эпицикла. Для этого нужно было проводить наблюдения планет, когда они удалены от точки противостояния с Солнцем. И здесь требовалось большое число наблюдений для каждой планеты. При этом для трех внешних планет — Марса, Юпитера и Сатурна — теория эпициклов оказалась очень точно воспроизводящей видимые движения этих планет. Гораздо хуже обстояло дело с Меркурием и Венерой. Чтобы спасти положение, Птолемею пришлось допустить периодические изменения наклона плоскостей эпициклов этих планет по отношению к плоскостям их деферентов (не говоря о том, что для всех планет — как внешних, так и внутренних — допускалась возможность наклона плоскости деферента по отношению к плоскости эклиптики). Эти «качания» делали картину совсем запутанной. Птолемей, видимо, сам чувствовал принципиальную неудовлетворительность столь сложной теории, потому что в тринадцатой (последней) книге «Альмагеста» он высказывает следующие соображения: «Пусть никто, глядя на несовершенство наших человеческих изобретений, не считает предложенные здесь гипотезы слишком искусственными. Мы не должны сравнивать человеческое с божественным... Просто небесные явления нельзя рассматривать с точки зрения того, что мы называем простым и сложным, так как у нас — все произвольно и переменно, а у небесных существ — все строго и неизменно, так что их движения по орбитам нельзя представлять себе вынужденными и трудными». В своей теории эпициклов Птолемей наряду с собственными наблюдениями и данными Гиппарха и других своих предшественников использовал богатейшие материалы многовековой работы вавилонских астрономов, на которых он сам прямо и многократно ссылается. Таким образом, в «Альмагесте» произошло органическое слияние греческой теоретической астрономии с достижениями восточной науки. В то же время нельзя недооценивать вклада самого Птолемея в методы астрономических наблюдений и расчетов. Если раньше (в том числе и у вавилонян) движение планет изучалось только по отношению к долготе, то Птолемей начал учитывать их перемещения по широте; созданная им методика впоследствии была почти целиком принята Коперником. В пределах точности наблюдений, производимых невооруженным глазом, эта методика давала достаточно хорошие результаты. Но Птолемей был сыном своего времени. Наряду с научной астрономией он много занимался астрологией и написал по этому вопросу фундаментальное сочинение — так наз. «Тетрабиблос» («Четырехкнижие»). Этот факт в большей степени, чем что либо другое, характеризует то противоречивое положение, в котором оказалась античная паука в период своего заката. |
загрузка...
