Математика
|
В предыдущей главе мы уже указывали па тот странный факт, что после Аполлония Пергского в эллинистической математике не появилось ни одного большого имени. Примерно около столетия длилась эпоха «эпигонов», затем наступил двухвековой перерыв — как если бы математикой в это время вообще никто не занимался. Новый подъем намечается лишь к концу I в. н. э., т. е. уже в эпоху Римской империи. Двумя выдающимися математиками этого времени были Герон и Менелай — оба из Александрии.
Герон более известен как талантливый инженер и изобретатель, но эта сторона его деятельности будет освещена ниже. Об его интересе к математике свидетельствует прежде всего тот факт, что он написал комментарий к «Началам» Евклида. Однако математика прежде всего была для него важна своими прикладными аспектами. До нас дошла «Метрика» Герона — сочинение, в котором собраны всевозможные формулы, использовавшиеся для измерения и для вычисления фигур. Среди них приводится и доказывается Формула, служащая для определения площади треугольника по трем его сторонам и приводимая в наше время в любом учебнике геометрии под именем «Формулы Герона» (имеются, впрочем, указания, что эта формула была известна еще Архимеду). Помимо точных формул, Герон приводит ряд приближенных правил; так, для извлечения квадратного корня он применяет правило, взятое, по-видимому, из вавилонской математики: 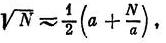
где а2 — наибольший целый квадрат, меньший N. Есть у него правило и для извлечения кубического• корня. Эти и многие другие правила он формулирует без доказательств, лишь поясняя их числовыми примерами. Менелай Александрийский был математиком совсем иного рода. В области тригонометрии он был продолжателем Гиппарха и написал книгу, ныне утерянную, о вычислении хорд (что эквивалентно вычислению синусов). Кроме того он заложил основы новой науки — сферической тригонометрии. В арабском переводе до нас дошла его «Сферика», состоящая из трех книг. В двух первых книгах доказываются различные теоремы о сферических треугольниках (между прочим, • теорема о равенстве). 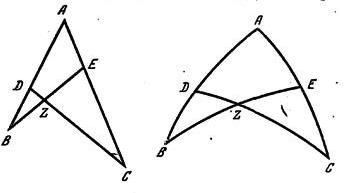
Рис. 13. К «теореме о трансверсалях» Мснелая на плоскости Рис. 14. К «теореме на трансверсалях» Менелая на сфере Третья книга начинается с «теоремы о трансверсалях», состоящей в следующем. Пусть даны две прямые АВ и АС и на них взяты две произвольные точки D и Е, и пусть CD и BE пересекаются в точке Z (рис. 13). Тогда можно доказать, что между отрезками, получившимся на чертеже, существуют такие соотношения: 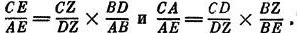
Посредством проектирования из центра Менелай переводит эти отношения на сферу (рис. 14) и, если ADB, АЕС, CZD и BZE будут большими кругами сфер, получает отношение для хорд: 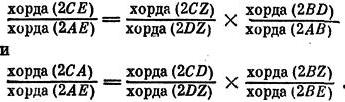
Из теоремы о трансверсалях Менелай получает ряд формул сферической тригонометрии. Доказанная Менелаем «теорема о трансверсалях» нашла потом широкое применение у Птолемея. Вообще вся эта область математики разрабатывалась тогда в качестве математического аппарата для астрономии; тем не менее книга Менелая представляла собой значительное достижение и с чисто математической точки зрения. Клавдий Птолемей был также несомненно прекрасным математиком, хотя математика интересовала его главным образом лишь как средство для решения астрономических и картографических задач. Но он не чуждался и чисто математической проблематики, о чем свидетельствует то, что им было написано сочинение о параллельных линиях и о пятом постулате Евклида (о чем сообщает Прокл). Текст этого сочинения утрачен и сколько-нибудь детальными сведениями о его содержании мы не располагаем (неоплатоник Прокл приводит якобы птоломеево доказательство пятого постулата Евклида, содержащее грубую ошибку). Следует отметить, что в «Альмагесте» Птолемеи широко пользуется заимствованной у вавилонян шестидесятеричной системой нумерации, применяя ее не только для дуг круга, но также для отрезков и площадей. Таким образом, «минуты», «секунды» и т. д. становятся у него отвлеченными числами, не связанными с каким-либо определенным видом величины. Любопытно, что в его записи дробей существовал символ о («омикрон»), служивший для обозначения отсутствия одного из шестидесятеричных разрядов. Это — первое появление нуля в европейской математической литературе. В лице Диофанта, величайшего математика III века н. э., мы встречаемся с представителем нового, алгебраического направления в античной математике, которое не находилось пи в какой связи с традиционной греческой геометрией. В свете новейших открытий в области ориенталистики можно считать вероятным, что корни алгебры Диофанта (так же, как и приближенных формул Герона) восходят к вавилонской математике. К сожалению, мы не располагаем никакими промежуточными звеньями, которые позволили бы нам проследить процесс переноса вавилонских алгебраических методов на эллинистическую почву. О жизни и личности Диофанта у нас нет никаких сведений, если не считать стихотворной эпиграммы-задачи, из которой следует, что Диофант прожил 84 года. Основное сочинение Диофанта — «Арифметика» — посвящено «достопочтеннейшему Дионисию». Мы знаем, что в середине III в. п. э. епископом Александрии был Дионисий; если в посвящении речь идет именно о нем, то это почти единственное указание на время жизни Диофанта, которым мы располагаем. «Арифметика» состояла из тринадцати книг, из которых до нас дошли только шесть. Уже само построение «Арифметики» существенно отличается от дедуктивно-аксиоматического способа изложения, принятого в классической греческой математике. «Арифметика» представляет собой собрание задач, которые решаются независимо друг от друга; эти решения подчас бывают очень остроумны, хотя, по видимости, не претендуют на всеобщность. Было бы, однако, неправильно считать, что Диофант не владел общими методами или недооценивал их значения. В первой книге Диофант рассматривает задачи, приводящие к определенным квадратным уравнениям. Судя по всему, он умел решать эти задачи не хуже вавилонян и индийцев, причем в эпоху Диофанта, по-видимому, уже существовала устойчивая традиция решения таких задач. Начиная со второй книги, Диофант рассматривает главным образом неопределенные уравнения — сначала второго, а потом и более высоких порядков. В Европе нового времени «Арифметика» стала известна в XVI в.; развитые Диофантом методы решения неопределенных уравнений оказали огромное влияние на Виета и Ферма. Эти методы находятся в таком же отношении к позднейшей алгебре и теории чисел, в каком архимедовы методы вычисления площадей и объемов находятся к анализу бесконечно малых. Для обозначения алгебраических выражений Диофант впервые ввел буквенную символику, сделав тем самым важный шаг вперед как по сравнению с числовой алгеброй вавилонян, так и по сравнению с греческой геометрической алгеброй классического периода. В его сочинении алгебра впервые находит свой собственный, присущий ей язык; правда, этот язык очень отличается от алгебраической символики нашего времени. Так, например, у Диофанте еще нет знака +; если нужно сложить несколько членов, он просто пишет их друг за другом. Для вычитания же у него существует особый символ 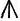 (можно ли рассматривать этот символ как обозначение отрицательного числа, остается неясным). В качестве примера укажем, что выражение (можно ли рассматривать этот символ как обозначение отрицательного числа, остается неясным). В качестве примера укажем, что выражение
x3+8x-(5x2+1) выглядит в записи Диофанта следующим образом: 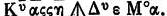
Последним выдающимся математиком александрийской школы был Папп, живший в конце III — начале IV вв. Он составил комментарий к «Началам» Евклида, к «Альмагесту» Птолемея и к некоторым другим сочинениям, но его важнейшим трудом был «Математический сборник» («Synagogc»), состоявший из восьми книг, из которых большая часть до нас дошла. В этом сочинении Папп собрал все, что он нашел интересного в трудах свои предшественников; по этой причине «Сборник» является бесценным источником сведений о содержании утерянных книг Евклида, Аполлония и других греческих математиков. Кроме того, в ряде случаев Папп приводит свои собственные результаты, показывающие, что он был не только компетентным компилятором, но и творческим исследователем высокого класса. Наибольшее значение имеют доказанные им теоремы, относящиеся к изучению кривых на торе и других поверхностях. Некоторые теоремы Паппа, вновь доказанные в XVII в. Дезаргом и Паскалем, положили начало проективной геометрии как особой ветви математической науки. В конце IV в. в Александрии жил математик Теон, написавший комментарий к «Альмагесту» и заново издавший «Начала» Евклида. Он известен главным образом как отец знаменитой Гипатии, трагическая гибель которой в 418 г. символизировала конец александрийской научной школы. Гипатия была единственной женщиной в истории античной науки; о ее собственных трудах известно только то, что она занималась платоновской философией и писала комментарии к Аполлонию и Диофанту. В V в. математическая мысль еще продолжает теплиться в Афинах. Так, неоплатоник Прокл написал комментарий к первой книге «Начал» Евклида, интересный тем, что в нем дается краткий очерк истории геометрии от Фалеса до Евклида. Заслуживает также упоминания Евтокий (VI в.), выдающийся комментатор Архимеда и Аполлония; труды этих ученых до сих пор издаются с его комментариями. |
загрузка...
