«Малые» математики эпохи эллинизма
|
Наряду с гигантскими фигурами Евклида, Архимеда и Аполлония в Александрии и в других культурных центрах III—II вв. до н. э. жили и работали математики меньшего калибра, не давшие новых идей и не разработавшие принципиально новых теорий. И все же некоторые из них заслуживают того, чтобы их имена не были преданы забвению.
О Кононе Самосском, старшем друге Архимеда, мы уже упоминали выше. О его собственных математических достижениях нам ничего не известно; впрочем, он был, по-видимому, скорее астрономом, чем математиком. Математические труды другого друга Архимеда — Эратосфена Киренского — были не столь значительны, как его работы в области географии и хронологии, но они все же свидетельствовали об оригинальном и творческом уме их автора. Так, Эратосфен дал механическое решение знаменитой задачи об удвоении куба; это решение было высечено на стене одного из александрийских храмов. Он занимался теорией чисел и предложил оригинальный способ выделить простые числа из последовательности всех нечетных чисел (так называемое «решето Эратосфена»). В диалоге «Платоник» он изложил основы античной арифметики, где, в частности, были сформулированы правила образования различных пропорций. 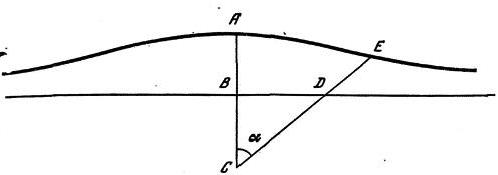
Рис. 9. Конхоида (или кохлоида) Никомеда. При любом А (меньше 90°) AB=DE Старший современник Аполлония, Никомед, известен главным образом тем, что открыл новую алгебраическую кривую — конхоиду. Она определяется как геометрическое место точек, образуемое концами лучей, исходящих из точки О и пересекающих прямую, причем расстояние от этой прямой до конца луча остается всегда равным а (рис 9). В полярных координатах уравнение этой кривой имеет вид: 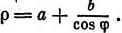
Как рассказывают источники, Никомед очень гордился этой кривой и построил прибор для ее черчения. Он применил свою кривую для решения задач об удвоении куба и трисекции угла. Ко второй половине II в. до н. э. относится творчество Диокла, изучавшего другую алгебраическую кривую — циссоиду. Она строится следующим образом. Даны два взаимно перпендикулярных диаметра круга АВ и CD. Пусть точки К и L удаляются от B в обе стороны, все время, однако, оставаясь на равном расстоянии от диаметра АВ. Из точки L опустим на диаметр CD перпендикуляр. Пересечение этого перпендикуляра с прямой KD даст нам точку, которая, по мере удаления К и L от В, будет описывать циссоиду (рис. 10). С помощью этой кривой Диокл также решил задачу об удвоении куба. Кроме того, он предложил свое решение задачи Архимеда о делении шара в заданном отношении; это решение, однако, было утеряно еще в древности. 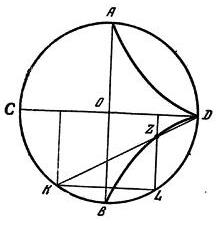
Рис. 10. Построение циссоиды Между III в. до н. э. и па-чалом нашей эры жил Зенодор — автор трактата «Об изопериметрических фигурах», где в частности, было показано: 1) что из двух правильных многоугольников с равными периметрами большую площадь будет иметь прямоугольник с большим числом сторон; 2) что если окружность круга и периметр правильного многоугольника равны, то площадь круга будет всегда больше правильного многоугольника; 3) что из всех многоугольников равного периметра и с равным числом сторон наибольшую площадь будет иметь правильный многоугольник. Следствие этих теорем состоит в том, что из всех изопериметрических фигур круг будет иметь наибольшую площадь. Зенодор также утверждал, что из всех пространственных тел с одинаковой поверхностью наибольшим объемом будет обладать шар. Это, вообще говоря, правильное предложение, им не было доказано; он сумел доказать лишь следующие теоремы (которые в его сочинения шли под номерами 13 и 14): 1) Если правильный многоугольник с четным числом сторон вращать вокруг самой длинной его диагонали, то получится тело, ограниченное коническими поверхностями, которое будет меньше шара с такой же поверхностью. 2) Каждый из пяти правильных многогранников будет меньше шара с той же поверхностью. Наконец, следует назвать Гипсикла, живущего в Александрии во II в. до н. э. Он написал сочинение о правильных многогранниках, по своему содержанию примыкавшее к XIII книге «Начал» Евклида; вероятно, именно поэтому оно было позднее включено в «Начала» в качестве XIV книги и таким образом дошло до нашего времени. В этом сочинении Гипсикл рассматривает додекаэдр и икосаэдр, вписанные в один и тот же шар, и показывает, что объемы этих двух фигур относятся друг к другу так же, как их поверхности. Кроме того, он доказывает, что указанное отношение будет равно отношению ребра вписанного куба к ребру икосаэдра. Других чисто математических работ Гипсикла мы не знаем; впрочем, в источниках имеется указание на то, что он писал о многоугольных числах, примыкая, таким образом, к пифагорейской традиции. Диокл, Зенодор и Гипсикл (и вообще все математики эллинистической эпохи, жившие после Аполлония) обычно именуются «эпигонами». Они действительно были эпигонами — в том смысле, что к основному богатству античной математики, накопленному гениями IV—III вв. до н. э., они добавили лишь мелочи, не выходившие за рамки уже существовавших идей и теорий. |
загрузка...
