3. Картографическая технология

Более полувека, прошедшего с момента зарождения геногеографической идеи до её современного воплощения, -срок достаточно большой, чтобы раскрылись те её стороны, которые первоначально оставались в тени, и принципиальная важность которых в начале не была определена. Мы имеем в виду карту как инструмент геногеографического исследования. Перефразируя утверждение академика Д. Н. Анучина, можно сказать, что степень геногеографического познания генофонда страны определяется степенью совершенства имеющейся для него карты. Современная геногеография уже немыслима без компьютерной картографии как её основы. Картографический анализ не только обеспечивает создание математически строгих, объективных и унифицированных карт, но и создаёт совершенно новые возможности для анализа явлений, моделируемых геногеографическими картами. По мысли А. С. Серебровского, геногеография способна обнаруживать главнейшие процессы, происходящие в генофонде. И лучше всего она это делает с помощью карт. На современном этапе развития геногеография имеет многообразный картографический инструментарий для корректного решения сложных задач. Именно картографическое исследование географической архитектоники генофонда позволяет анализировать географию и историю процессов, формирующих основные свойства генофонда.

Вся сложность ситуации заключалась в том. что вопрос о карте как инструменте геногеографии не был поставлен А. С. Серебровским, создававшим науку геногеографию. Именно поэтому в дальнейшем на долгое время возобладал чисто статистический анализ популяций, изъятых из географического пространства. Карты географического распространения генов, особенно генов и фенотипов человека, создавались, а чаше — рисовались и до, и после постановки А. С. Серебровским проблем геногеографии. Некоторые прекрасные работы, основанные на строгом картографическом методе, остались малоизвестны и незаслуженно забыты [Чепурковский, 1913]. Другие, представляющие результат иллюстрирования, а не картографического анализа распределения генов, широко известны [Mourant et al., 1976].

КОМПЬЮТЕРНОЕ КАРТОГРАФИРОВАНИЕ

Лишь с 70х годов XX века начал формироваться картографический подход к геногеографии - как на путях создания цифровых моделей карт, так и на путях математического анализа и точного отображения трендовых явлений на карте [Cavalli-Sforza, Bodmer, 1971; Ward, Neel, 1976; Rychkov, Sheremetyeva, 1977, 1979]. На рубеже 80х годов, благодаря органическому соединению с картографией и с созданием компьютерных банков данных о частотах генов в населении, начался принципиально новый этап в развитии геногеографии - компьютерное генетическое картографирование [Menozzi et al., 1978; Piazza et al., 1981a, 19816, Ammerman, Cavalli-Sforza.1984]. Геногеография популяций человека пережила и в переносном, и в буквальном смысле второе рождение: возник журнал Gene Geography (1987 г.). Как ни печально, его учредители не догадывались ни о происхождении и долгой предыстории геногеографии, ни о её связи с исследованием генофонда, и полагали, что созданием журнала оформили те идеи, что витали в европейской науке в 60 х годах нашего столетия [Terrenato, личное сообщение]. Возможно, именно поэтому журнал был ориентирован исключительно на публикацию данных о частотах генов в населении мира, оставляя за рамками своих публикаций проблемы не только генофонда, но и генетической картографии.
Как бы то ни было, началась эпоха компьютерной геногеографии и создания электронных карт географического распределения генетической информации. Это означает, что появилась практическая возможность от географии генов человека перейти к географии генофондов населения мира, регионов, отдельных стран и этнических групп. Появилась возможность исследовать генофонд не только общими генетико-статистическими методами, но и собственными уникальными методами геногеографии -картографическими.
Широкие возможности компьютерных карт и заставили нас взяться за их создание. При этом мы прошли долгий путь, причём полностью независимо от коллектива L. L. Cavalli-Sforza. Их «синтетические» карты мы увидели тогда, когда уже были созданы наши «обобщённые» карты. Тем более впечатляюще и закономерно, что оба коллектива независимо шли параллельными путями. Эти пути ни в чем не повторяли друг друга, однако при этом все общие инструменты картографирования оказались очень похожи. Поэтому мы не будем в этой книге останавливаться на анализе сходства и различий в технологиях - достаточно того, что получаемые карты обоих коллективов полностью сопоставимы.

ТРИАНГУЛЯЦИОННЫЕ КАРТЫ

На рубеже 80х годов - ещё до эпохи персональных компьютеров - один из авторов этой книги вместе с профессором Ю. Г. Рычковым и известными специалистами в области математического моделирования А. Т. Терехиным и Е. В. Будиловой начали разрабатывать первый вариант программного обеспечения для компьютерного картографирования. К сожалению, этот вариант так и не был опубликован. В его основе лежала триангуляционная процедура, использующая метод ближайшего соседа. Она позволяла строить и в целом корректные карты частот отдельных генов, и «обобщённые» карты - главных компонент изменчивости генофонда в целом. Иными словами, этот вариант программного обеспечения позволял создавать все те карты, которые примерно в это же время независимо разрабатывал коллектив под руководством L. L. Cavalli-Sforza [Menozzi et al., 1978; Piazza et al., 1981а]. Однако триангуляционная процедура построения карт приводила к трудно устранимому недостатку - на границах ареала значения признака были неустойчивыми. Были ещё несколько особенностей этой процедуры. Основную проблему составляло то, что такую карту было сложно «накрыть» равномерной сеткой и создать полностью сравнимые числовые матрицы разных карт. Эти особенности не позволяли решить сверхзадачу - сделать любую карту не только результатом, но и объектом следующего вида анализа.

АНАЛОГОВЫЕ КАРТЫ

Это заставило нас приступить к созданию нового программного пакета, реализованного программистом А. В. Рычковым [Рычков и др., 1990; Балановская и др., 1990]. В нем был использован принцип интерполяции, моделирующий распространение генов из изученных популяций на все промежуточные области. Эту процедуру мы называли технологией «чернильных пятен». Ее можно представить как «растекание» разноцветных чернильных пятен. На первом шаге - в каждую точку карты, где имеется изученная популяция, наносится такое «пятно», цвет которого соответствует концентрации частоты гена. На следующем шаге - пятна начинают расплываться во всех направлениях. На каком-то шаге итерации - соседние пятна начинаются смешиваться, реализуя некие промежуточные значения. Чем больше шагов итерационной процедуры - тем сильнее взаимовлияние даже самых отдалённых популяций и тем более «усреднённая» карта возникает перед нами. При этом сохранялась географическая локализация исходных частот генов - благодаря «маскированию» исходного значения частоты в фиксированной точке пространства. Важнейшим достоинством этого метода построения карт было то, что значения частот генов в обследованных географических точках (взаимное расположение которых могло быть сколь угодно нерегулярным) интерполировалось на узлы регулярной сетки. В результате мы получали двумерную цифровую матрицу, с которой можно было проводить любые операции одно- и многомерной статистики. Иными словами, решали нашу сверхзадачу - любая карта могла стать объектом следующего вида анализа. С помощью этого программного пакета были построены различные типы «синтетических» карт - и главных компонент, и генетических расстояний [Балановская и др., 1990] для популяций Центральной Азии и Кавказа.
У этого программного пакета было неоценимое достоинство перед всеми остальными (в том числе, и ныне широко используемыми) технологиями - он создавал как бы аналоговую модель миграции генов. Но все же и он не полностью удовлетворял нашим требованиям. Например, надо было волевым решением выбирать шаг, на котором останавливалась итерация. А основной недостаток заключался в том, что метод не позволял разделить две процедуры - создания карт только на основе исходных данных и «сглаживания» этих карт, то есть устранения случайных флуктуаций для выявления основных паттернов изменчивости. Эти обе процедуры протекали как бы одновременно - в процессе построения карты с числом итераций возрастало и «сглаживание» карты. В результате создавались сразу карты трендов (как и в технологии коллектива L. L. Cavalli-Sforza), а исходная «несглаженная» карта оставалась неизвестной. Этот серьезный недостаток заставил нас искать иные принципы создания карт.

КАРТЫ СРЕДНЕВЗВЕШЕННОЙ ИНТЕРПОЛЯЦИИ

Поэтому в 1990 г. было начато создание третьего варианта программного пакета, который и лег в основу всех последующих компьютерных карт, в том числе и приведённых в данной книге. Он создавался в долгой совместной работе с сотрудниками кафедры картографии МГУ, которыми руководил С. М. Кошель. Пакет использовал известную библиотеку программ MAG; проблемы визуализации цифровых матриц были решены с помощью оригинального пакета «Metacopy», а статистические разделы программы сначала разрабатывались нами совместно с сотрудниками кафедры картографии МГУ (С. М. Кошель. Д. Б. Патрикеев, А. В. Асриев, О. Р. Мусин, В. В. Иванов), а затем с помощью своих программистов (И. А. Краснов, В. Е. Папков, Т. П. Папкова, А. В. Рычков, С. Д. Нурбаев и др.).

Путь по созданию программного пакета необходимо было пройти вместе географам и генетикам. Ведь геногеография имеет собственный предмет исследования - пространственную структуру генофонда. При этом генофонд, с одной стороны, является объектом популяционной генетики, другой стороны - выступает как один из множества объектов тематической картографии [Берлянт, 1986; Трофимов, Панасюк. 1987]. Поэтому компьютерная технология геногеографического анализа генофонда не могла быть просто перенесена из географии, не имеющей дела с генетической информацией. Она создавалась в сотрудничестве с географами, картографами и математиками специально для геногеографического изучения генофонда.
В результате в технологии картографического изучения генофонда максимально учтены и использованы методы картографической науки: методы построения интерполяционных карт, правила оформления карт, принцип анализа фоновых поверхностей. Однако сама технология картографо-статистического моделирования и анализа направлена на решение задач популяционной генетики [Балановская и др.. 1990; 1994а,б; 1995; 1997 и др.]. Созданный многообразный арсенал средств целиком задан принципами и логикой анализа генофондов. Корреляционный анализ и анализ показателей генетического разнообразия. картографирование главных компонент и размещение популяций в их пространстве, техника «меняющегося» окна и анализ генетических расстояний, оценка надёжности картографического прогноза и многие другие методы статистического анализа карт разрабатывались специально для задач изучения генофонда.
Совокупность этих методических разработок трудно определить однозначно. В целом они относятся к тематической картографии, по классификации методов - к нескольким разделам математико-картографического моделирования [Берлянт, 1986; Трофимов, Панасюк, 1987]. Наиболее корректно их обозначить как картографо-статистические методы. Их общая цель: дать количественное выражение информации, содержащейся в геноге-ографической карте; выявить и выразить ту информацию, которая находится в неявном виде (закономерности, тренды, связи и т. д.); провести одно- и многомерный статистический анализ карт для выявления важнейших характеристик генофонда. Вся процедура картографо-статистического анализа генофонда основана на оригинальном программном обеспечении, что позволило создать своего рода компьютерную технологию геногеографического скрининга генофонда.
На основе созданной технологии были построены картографические модели различных параметров не только генофонда, но и целого спектра иных признаков, имеющих отношение к пространственной структуре популяций. Это и характеристики среды - как природные (климатические), так и антропогенные факторы (техногенные нагрузки); и характеристики материальной культуры; и частоты фамилий; и особенности размера популяций и инбридинга; и картографический анализ моногенной патологии [Балановская и др., 1996, 1997, 2000; Грехова и др., 1996; Перепелов и др., 1996; Евсюков и др., 1996, 1997; Петрин и др., 1997; Почешхова, 1998; Почешхова и др., 1998; Spitsyn et al., 1998; Гинтер и др., 1998].

ЗАРУБЕЖНЫЕ ПРОГРАММНЫЕ ПАКЕТЫ

Кроме трех перечисленных отечественных картографических пакетов, существует и ряд иных программ, используемых в зарубежных работах по геногеографии.
Наибольшее значение для геногеографии имел пакет программ, используемых группой L. L. Cavalli-Sforza. Этот пакет позволяет проводить как картографирование отдельного гена, так и расчёт синтетических карт главных компонент, хотя и не предусматривает другие виды статистического анализа и трансформации карт. Похожие, хотя и ешс менее мощные программы разрабатывались и некоторыми другими коллективами популяционных генетиков [например, Sokal, 1999а,б].
А в последние годы определенную популярность приобрела программа Surfer (Golden Software Surfer 7.0). Этот картографический пакет не является геногеографическим, а предназначен для картографирования любых, в первую очередь климатических параметров. Но он позволяет быстро построить интерполяционные карты любых признаков - в том числе и распространения генов, и поэтому нередко используется в современных работах для картографирования распространения гаплогрупп митохондриальной ДНК и Y хромосомы [Semino et al., 2000; Rootsi et al., 2004]. Но у программы Surfer есть очень крупный недостаток, отличающий её от остальных картографических программ, используемых в геногеографии. Это отличие состоит в том, что карты, построенные Surfer, являются только изображениями. Программа нацелена только на графический результат, а не на создание цифровой модели карты. То есть для каждой точки карты нельзя получить точные численные значения признака, а значит, нельзя проводить никакие виды картографо-статистического анализа, нельзя рассчитать карты главных компонент и так далее. Программа Surfer, таким образом, оказывается весьма эффективной для иллюстрации, для изображения распространённости отдельных признаков, но не позволяет проводить статистический анализ карт и строить все множество производных карт, в том числе синтетических. Иными словами, она позволяет картографировать распространённость отдельных генов, но не позволяет изучать генофонд.
Наибольшее значение для геногеографии имел пакет программ, используемых группой L. L. Cavalli-Sforza. Этот пакет позволяет проводить как картографирование отдельного гена, так и расчёт синтетических карт главных компонент, хотя и не предусматривает другие виды статистического анализа и трансформации карт. Похожие, хотя и ешс менее мощные программы разрабатывались и некоторыми другими коллективами популяционных генетиков [например, Sokal, 1999а,б].

А в последние годы определенную популярность приобрела программа Surfer (Golden Software Surfer 7.0). Этот картографический пакет не является геногеографическим, а предназначен для картографирования любых, в первую очередь климатических параметров. Но он позволяет быстро построить интерполяционные карты любых признаков - в том числе и распространения генов, и поэтому нередко используется в современных работах для картографирования распространения гаплогрупп митохондриальной ДНК и Y хромосомы [Semino et al., 2000; Rootsi et al., 2004]. Но у программы Surfer есть очень крупный недостаток, отличающий её от остальных картографических программ, используемых в геногеографии. Это отличие состоит в том, что карты, построенные Surfer, являются только изображениями. Программа нацелена только на графический результат, а не на создание цифровой модели карты. То есть для каждой точки карты нельзя получить точные численные значения признака, а значит, нельзя проводить никакие виды картографо-статистического анализа, нельзя рассчитать карты главных компонент и так далее. Программа Surfer, таким образом, оказывается весьма эффективной для иллюстрации, для изображения распространённости отдельных признаков, но не позволяет проводить статистический анализ карт и строить все множество производных карт, в том числе синтетических. Иными словами, она позволяет картографировать распространённость отдельных генов, но не позволяет изучать генофонд.
Процедуры построения и анализа компьютерных карт пакетом GGMAG подробно описаны в целом ряде специальных публикаций [Балановская и др., 1994а,б, 1995, 1997, 1998; Сербенюк и др., 1990. 1991; Нурбаев, Балановская, 1998; Балановский и др. 1999]. Поскольку описание картографической технологии - тема будущей книги, мы укажем здесь лишь на ключевые моменты технологии. Для вдумчивого читателя мы постараемся называть разделы, посвященные тому или иному методу, в соответствии с терминологией картографического арсенала (§3 предыдущего раздела 2). Иные пояснения даются в других местах книги по мере необходимости.

ОТ РАЗБРОСАННЫХ ПОПУЛЯЦИЙ К РЕГУЛЯРНОЙ КАРТЕ

Данные о генофондах обычно крайне нерегулярны. Достаточно взглянуть на любую таблицу, чтобы увидеть, как неравномерно изучены гены - по каждому генетическому маркёру изучен свой набор популяций. С другой стороны, достаточно взглянуть на любую карту, чтобы увидеть, как неравномерно разбросаны изученные популяции. В этом проявилось не только «бесплановость» изучения генофонда, но и объективный фактор: резкие различия в численности и плотности коренного населения в разных регионах. Однако для геногеографического анализа, в отличие от чисто статистического, обе эти неравномерности не являются серьёзным препятствием, поскольку предметом анализа становится карта, а не первичный популяционно-генетический материал.

ПОДХОДЫ К СОЗДАНИЮ КАРТЫ

Все геногеографические карты основаны на единых методических подходах:
1. Единицей геногеографического наблюдения является популяция, характеризующаяся частотой гена и ареалом.
2. Для геногеографического изучения региона выбираются популяции, находящиеся на одном уровне популяционной структуры, вне зависимости от размеров их ареала.
3. Геногеографическая карта должна обладать не только географическим, но и генетическим масштабом: например, мировой диапазон изменчивости частоты гена, континентальный, региональный, этнический. Выбор генетического масштаба диктуется задачами исследования.
4. В генетически изученных популяциях (опорных точках карты) размещается исходная (табличная) частота гена. В популяционных ареалах проводится интерполяция -то есть для всех точек ареала популяции рассчитывается частота признака на основе данных об опорных точках (изученных популяциях).
5. Мы стремились к методу интерполяции, требующему минимума исходных предпосылок и позволяющему изменять любые параметры построения карты. Это позволяет вместо одной карты признака создать множество её моделей. Совокупность таких моделей выявляет наиболее устойчивые черты географического распределения признака, не зависящие от параметров построения карты.
6. В основе метода интерполяции лежит принцип генетической проницаемости пространственных барьеров за достаточно длительный промежуток времени, то есть ненулевой вероятности генных миграций в любую точку пространства. Эта вероятность генных миграций для разных точек различна и зависит от географического расстояния между популяциями.
7. В анализе генофонда отдельные признаки играют служебную роль - они должны помочь выявить генетическую неоднородность пространства и пространственную неоднородность генофонда. Лишь игнорируя - в процессе построения карты - природные и социальные барьеры, можно рассчитывать, что созданные карты сами обнаружат существование в пространстве генетически значимых барьеров.
8. Для простоты чтения карты все непрерывное множество значений признака подразделяется на несколько групп - интервалов признака. Число и размер интервалов выбираются в зависимости от задачи исследования. Но для каждой карты размеры всех её интервалов одинаковы (равноинтервальная шкала). Размер интервалов зависит от генетических расстояний между популяциями, тогда как площадь, занимаемая тем или иным интервалом, зависит ещё и от размеров ареалов разных популяций.
9. Основная задача при построении карты - интерполяция значений частот признака в опорных точках (взаимное расположение которых может быть сколь угодно нерегулярным) на узлы регулярной картографической сетки.

ИЗОТРОПНОСТЬ ПРОСТРАНСТВА

Принципиально важно, что при построении карты географическое пространство предполагается изотропным. Это означает, в процессе создания карты не учитываются ни природные, ни историко-культурные факторы, безусловно, влияющие на распространение генов. Любой учет этих факторов субъективен - он всегда связан с экспертной оценкой значимости фактора для генофонда. Такая оценка порой больше зависит от эксперта, чем от фактора, и её учет вводил бы в строгую математическую модель карты субъективный фактор научного мировоззрения эксперта. Сама карта может объективнее эксперта учесть и отразить реальное воздействие как природных, так и историко-культурных факторов на генофонд. Если анизотропность физического и культурного пространства нашла отражение в самих наблюдаемых частотах генов, то она проявится и при картографировании: барьеры, препятствующие свободному потоку генов, создадут перепад частоты гена; и чем мощнее барьер, тем более резкий перепад частот мы обнаружим на карте.

§3. Простые карты

ИНТЕРПОЛЯЦИЯ

Как мы уже говорили, принципиально важно, что при создании карты можно из целого спектра предусмотренных вариантов выбрать наиболее корректный вариант
интерполяционной процедуры. В результате любой интерполяции по нерегулярно расположенным опорным точкам создается цифровая модель (ЦМ) генетического рельефа: рассчитываются значения признака в узлах регулярной сетки, покрывающей картографируемое пространство.
Полагая, что распределение признака на обширной и гетерогенной в природном и историческом отношениях территории не может определяться действием какого-либо единственного фактора микроэволюции, нами использован метод двумерной средневзвешенной интерполяции. Такая интерполяция более чувствительна к локальной геометрии распределения значений признака в опорных точках. Она может быть распространена не на всю территорию, а на область, ограничиваемую задаваемым радиусом действия весовой функции. Как и в модели изоляции расстоянием, такая интерполяция может использовать степенную зависимость значения признака от расстояния «узел сетки - опорная точка». Использована гипотеза линейного изменения частоты гена вдоль геодезической кривой, кратчайшим образом соединяющей две соседние точки карты. При этом длина каждой геодезической вычислялась на основе моделирования геоида Земли равновеликой сферой (по Красовскому).

ЦИФРОВАЯ МОДЕЛЬ

Итак, в основе компьютерных карт лежат их цифровые модели (ЦМ) - двумерные численные матрицы с прогнозируемыми частотами признака для каждого узла сетки карты. Это позволяет работать с картой как с обычной матрицей, осуществляя любые виды арифметических и алгебраических преобразований, используя любые методы одномерной и многомерной статистики, применяя методы иных разделов математической науки (например, теории надёжности).

Компьютерное картографирование, независимо от конкретной интерполяционной процедуры, всегда представляет собой создание цифровой модели карты. Значения цифровой модели (ЦМ) картографируемого признака рассчитываются для узлов регулярной сетки ЦМ по эмпирическим значениям признака в опорных точках - генетически изученных популяциях. Выражение «опорные точки» - не образ, а конкретный термин, поскольку исходные значения признака в изученных популяциях действительно служат опорой изображенной на карте поверхности распределения признака: поверхность как бы сетью «натянута» на ординаты значений картографируемого признака в этих точках, преобразуя несвязно разбросанные опоры в изгибы, вершины и впадины генетического рельефа. В узлах регулярной сети ЦМ находятся значения картографируемого признака, рассчитанные с помощью интерполяционной процедуры: ортогональных полиномов на основе информации обо всех исходных генетически изученных популяциях в пределах заданного радиуса. При расчёте полинома значение признака в каждой популяции берется с весом, обратным расстоянию от популяции до узла сетки; по совокупности всех изученных популяций рассчитывается среднее значение в каждом узле сетки: в результате проведения этой процедуры для каждого узла создается ЦМ карты [Сербенюк и др., 1990, 1991; Берлянт и др. 1991а,б; Koshel et al., 1991; Koshel, Musin. 1991. 1994; Koshel. 1992; Berlyant et al., 1992]. Таким образом расчёт ортогональных полиномов проводится согласно [Сербенюк и др., 1990].

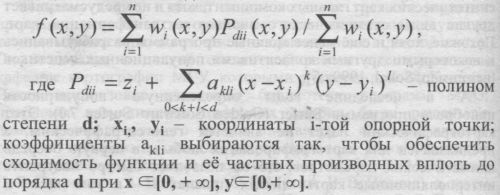
Например, для создания ЦМ карт русского генофонда, пространство карты было покрыто густой равномерной сетью, состоящей из 9000 узлов. Для каждого узла сетки с помощью интерполяционной процедуры рассчитано значение частоты гена: в расчёт входили все изученные популяции в пределах заданного радиуса, взятые с весом, обратным расстоянию от данного узла сетки до конкретной изученной популяции. В данном случае была использована нулевая степень полинома, шестая степень весовой функции и учитывалась информация об исходных популяциях в радиусе 2000 км от данного узла сетки. Такой расчёт проводился независимо для каждого узла сетки. Это означает, что для каждого из 9000 узлов сетки учитывались почти одни и те же изученные популяции, но расстояния до каждой популяции и, следовательно, её «вес» при определении частоты гена в данном узле сетки - менялись. Еще раз подчеркнём, что рассчитанные значения в каких-либо узлах сетки никак не влияют на определение частоты гена в других её узлах. И поэтому все равно, с какой именно точки начнётся построение карты.
После того, как для каждого узла сетки получен независимый прогноз частоты гена, можно считать, что цифровая модель (ЦМ) карты создана: у нас имеется двумерная матрица, в каждой ячейке которой (для каждого узла равномерной сетки) хранится прогнозируемое значение признака. Далее с ЦМ (как с обычными матрицами) проводим все дальнейшие преобразования и статистические расчёты - корреляций, трендов, расстояний, главных компонент, - получая количественные оценки связей и закономерностей. При этом карта становится не иллюстрацией, а математической моделью пространственной изменчивости. Она служит инструментом количественного анализа генофонда: то есть становится не «графическим», а «алгебраическим» объектом.
Возникает закономерный вопрос: как меняются статистические характеристики (средняя частота признака, дисперсия и т. д.) в результате картографирования? Иными словами, насколько и как различаются характеристики опорных точек и ЦМ карты, созданной на их основе? Ответ на этот вопрос подробно рассмотрен в главе 5 (раздел 5.1., §5).

КАК ЗАВИСИТ КАРТА ОТ ПАРАМЕТРОВ ЕЕ ИНТЕРПОЛЯЦИИ?

Итак, построение простой карты можно представить себе следующим образом. Сначала создается картографическая основа, напоминающая контурную карту (со своими картографической проекцией, морями, реками и границами). На нее наносятся исходные точки - популяции, изученные по данному гену. А сверху накладывается как бы листок в клетку - равномерная прямоугольная сеть. И для каждого узла этой сетки рассчитывается новое, интерполированное значение частоты гена. В каждом узле такое значение определяется всей совокупностью исходных точек в пределах заданного радиуса, но исходные значения частот гена берутся с весом, обратно пропорциональным расстоянию dj: чем дальше исходная популяция от узла сетки, тем меньше её вес. После того, как расчёт проведён для каждого узла сетки и как бы занесён в каждую клетку, этот «листок в клеточку» становится цифровой матрицей (ЦМ) частоты гена. Для следующего гена повторяем ту же самую процедуру. И если для всех генов мы использовали строго одни и те же картографическую основу и равномерную сетку, то в результате получаем серию ЦМ всех генов - полностью сопоставимых и унифицированных.
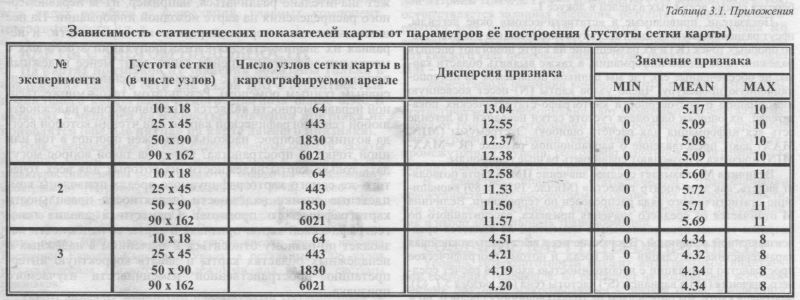
Параметры интерполяционной процедуры выбираются в соответствии с оптимальным значением дисперсии признака (по всем узлам карты). Например, в таблице 3.1. приведены значения статистических показателей карты в экспериментальной ситуации

ВИЗУАЛИЗАЦИЯ КАРТЫ

Итак, при статистическом анализе ЦМ предстает как двумерная матрица значений признака. При этом каждому узлу сети ЦМ соответствуют точные значения географических координат местности. Это позволяет перейти от матрицы к собственно картографическому образу.
Для формирования собственно карты как зрительного картографического образа создается электронная картографическая основа: контуры территории в заданных географических проекции и масштабе, гидрографическая сеть, внутренние водоёмы и омывающие моря, административные границы, опорные точки, градусная сеть; программно обеспечивается создание легенды карты. Пространственное распределение признака изображается на картографической основе с помощью группировки значений ЦМ в интервалы шкалы изменчивости признака. Интервалы на карте разграничиваются изолиниями.
При визуализации карты мы группируем значения признака в те или иные интервалы и окрашиваем их по аналогии с физической картой. На цветных картах наиболее низкие значения признака окрашиваются синими тонами морских впадин, средние - зелёным цветом равнин, высокие значения признака - красно-коричневыми оттенками гор. На черно-белых картах - повышение частоты признака выражается в большей интенсивности окраски. Основной принцип наших карт - использование равномерной шкалы интервалов.
При переходе от ЦМ к карте значения признака объединяются в интервалы, указанные в легенде карты, и послойно окрашиваются. Благодаря интервалам шкалы не только создается образ карты, но и косвенно учитывается доверительный интервал самих значений признака. Области, окрашенные одним цветом, читаются как области, характеризуемые значением признака, варьирующим в пределах, указанных в легенде шкалы интервалов. Изолинии, соединяющие точки с одинаковым значением признака, рассматриваются как вспомогательные линии при чтении карты, а не как области точных значений.

Итак, при визуализации карты отображается не только её основное содержание, то есть значения признака и разделяющие их изолинии, но и ряд географических объектов на картографируемой территории, помогающие читателю соотнести карту с известным ему географическим пространством. Практически на каждой геногеографической для одного из регионов. Проведены три эксперимента. В каждом из них географические координаты популяций карте отображаются моря (береговая линия), озера и реки, государственные и этнические границы, города, а на некоторых картах могут отображаться и дополнительные объекты (ледники, горы и другие). Также показывается расположение исходных изученных популяций (опорных точек), отображаемых ромбиками или кружками. Для облегчения чтения карт мы обычно приводим не только гидрографическую сеть, но и названия нескольких крупных городов (независимо от того, были они изучены по данному признаку или нет). Легенда карты не только помогает понять её содержание, но и несет большой объём статистической информации.

ЛЕГЕНДА КАРТЫ

Каждая карта сопровождается легендой, которая может включать до четырех окон: статистическое окно, гистограмму картографированных значений, гистограмму исходных значений, гистограмму со стандартными граничными значениями.

ГИСТОГРАММЫ. Вариационно-статистическое распределение признака на карте (гистограмма) дается в одном из окон легенды в виде гистограммы, имеющей, как указывает Г. Ф. Лакин, «не только иллюстративное, но и аналитическое значение» [Лакин, 1980, с. 293]. Штриховка гистограммы соответствует штриховке интервалов на карте. Над столбцами гистограммы указана в % доля площади, занятая данным интервалом частот.
При необходимости на картах приводятся также две других гистограммы: а) вариационно-статистическое распределение исходных значений признака (в опорных точках), построенное в тех же интервалах, что и карта в целом. Сравнение гистограмм исходных и картографированных значений признака позволяет оценить новую информацию, которую вносит учет ареала при картографировании признака; б) вариационно-статистическое распределение картографированных значений признака в универсальной шкале: например, для частот генов - от 0 до 1. Это дает возможность сохранять единый генетический масштаб при сравнении распределений различных генов.

СТАТИСТИЧЕСКОЕ ОКНО ЛЕГЕНДЫ содержит, как правило, следующие показатели:

К - число опорных точек (их географическое положение приведено на карте);
N - число узлов регулярной сетки (число значений матрицы ЦМ);и значения картографируемого признака задавались случайным образом. В каждом эксперименте изменялся только один параметр - густота сети (от 64 до 6021 узлов). Таблица 3.1. демонстрирует, что даже при увеличении в 100 раз густоты сетки ЦМ, изменения в оценке средних и дисперсий картографируемого признака невелики. Та густота сетки, которой соответствует «перегиб» кривой значений дисперсий (минимум), принята оптимальной.

MIN, MAX, M, S² - экстремумы, средняя и варианса признака, где M = Σp_ij/N; S² = Σ(p_ij - M)²/N, p_ij - значение признака в узле матрицы ЦМ с координатами i и j.

H_T, H_S, G_ST - характеристики общего, внутри- и межпопуляционного генного разнообразия [Nei, 1975] (в качестве популяций выступают узлы сетки): H_T = M(1-M); H_S = H_T - D_ST; G_ST = D_ST/H_T ≈ F_ST; D_ST = S². Приведённые значения показывают вклад картографируемого аллеля в генное разнообразие локуса (L): H_T(L) = ΣH_T(i); D_ST(L) = ΣD_ST(i); H_S(L) = ΣH_S(i); G_ST(L) = ΣD_ST(i)/ΣH_T(i); берётся сумма всех i-тых аллелей в локусе L.

Показатели, приводимые в «статистическом» окне легенды, несут разнообразную вспомогательную информацию о карте. Число опорных точек (К) и их размещение на карте помогают оценить надёжность исходной информации, а также выявить области карты. не обеспеченные ею, где мы целиком полагаемся на интерполяционную процедуру. Число узлов карты (N) несет косвенную информацию о достоверности картографо-статистических показателей: их ошибки благодаря густоте сетки невелики (в легенде есть вся информация для расчёта ошибок). Экстремумы (MIN, МАХ) дают представление о вариационном размахе (R =МАХ-MIN) признака и позволяют сравнивать разные генофонды.
Величина М указывает среднее значение ЦМ, а карта позволяет видеть, как этот «центр тяжести» [Миллс, 1958, с. 89] вариационно-статистического ряда распределён по территории. Величина М отличается от среднего значения признака, рассчитанного по опорным точкам принципиальным моментом: М является средневзвешенной величиной. В качестве веса выступает важнейшая характеристика популяции — её ареал, и потому географическое пространство популяции с необходимостью входит в расчёт среднего значения (М) и вариансы (S2) частоты гена (см. раздел 5.1, §5). Благодаря карте, мы определяем не только величину средней, но и занятые ею области картографируемого пространства.

§4. Надёжность картографического прогноза

Компьютеры ненадёжны, но люди ещё ненадёжнее.
Законы ненадежности Джилба

Карта каждого гена сопровождается специальной картой надёжности, которая для каждого узла сетки указывает достоверность рассчитанного значения частоты гена.

ЧТО ТАКОЕ «НАДЁЖНОСТЬ» КАРТЫ

При решении задачи математического моделирования сушеструют два аспекта: 1) адекватность (то есть соответствие) предлагаемой математической модели анализируемым данным; 2) надёжность (то есть статистическая достоверность) результатов математического моделирования.
Если вопросы адекватности математических моделей геногеографии (их соответствия картографируемым данным, прогностической ценности и т. д.) анализировались целым рядом авторов, то работы по решению проблемы надёжности результатов картографирования в мировой литературе отсутствуют. Нерешённость проблемы надёжности картографирования не позволяет проводить строго объективную интерпретацию геногеографических карт, является основным мотивом справедливой критики и тормозит широкое использование геногеографических методов. Поэтому наша компьютерная технология геногеографического изучения генофонда уже несколько лет включает в себя оценку надёжности (достоверности) картографического прогноза - построение карт надёжности картографических моделей генофонда.
Новая характеристика «надёжность карты» количественно характеризует степень устойчивости анализируемых значений картографической модели. Надёжность измеряется вероятностью осуществления прогноза карты в каждой её точке и оценивает статистическую достоверность каждого картографированного значения.
Любая геногеографическая карта предлагает модель распространения признака (например, частоты гена) в географическом пространстве. Поскольку любое значение карты, полученное в результате интерполяционной процедуры картографического моделирования, является прогнозом, важно оценить, какова надёжность такого прогноза, какова вероятность его осуществления. Оценка надёжности дает ответ на вопрос: если в данной (любой) точке пространства провести изучение генофонда, то какова вероятность получить значение частоты гена, достаточно близкое к прогнозу, показанному на его карте?
Надёжность карты в разных частях её пространства может значительно различаться, например, из-за неравномерного распределения на карте исходной информации. На нее накладывается и неравномерность их изученности, и неравная их значимость для карты (популяции в регионах с мощными эффектами дрейфа генов дают менее надёжный прогноз, чем популяции с большой численностью и интенсивным генным обменом). Результатом такой множественной неравномерности является и неравномерная надёжность любой геногеографической карты, при чтении которой всегда возникает вопрос: насколько надёжен прогноз в той или иной точке её пространства? Ответ на такой вопрос могут дать только карты надёжности, на которых для всех точек того же самого картографируемого ареала приведены комплексные оценки надёжности (вероятности правильности картографического прогноза). Совместный анализ геногеографической карты признака и карты её надёжности позволяет по-разному относиться к значениям в надёжных и ненадёжных областях карты и давать корректную интерпретацию пространственной изменчивости изучаемого признака.
Карты надёжности создаются, исходя из основных положений математической теории надёжности. В биологических науках также используются приложения этой теории - при изучении экологических систем, генетических систем, клеток, клеточных популяций и тканей, процессов старения, репарации и др. При этом теория надёжности «рассматривается как важный эвристический метод исследования биологических объектов. Подобный подход возможен на любом уровне интеграции» [Кутлахмедов, 1985, стр. 7].

Из теории надёжности в геногеографию вводятся два понятия: уровень строгости (достоверности) α и вероятность прогноза Р [Нурбаев, Балановская, 1997, 1998; Балановская, Нурбаев, 1999].

1) УРОВЕНЬ СТРОГОСТИ (α). Уровень строгости служит постоянным коэффициентом при интегрировании дифференциального уравнения, описывающего надёжность анализируемой системы. Он задаётся в соответствии с требованиями надёжности к данной системе. Уровень строгости (обычно от α=0.3 до α=0.7) исследователь выбирается, исходя из требований к степени надёжности результатов, масштаба картографируемой территории, объёма доступной исходной информации.

2) ОЦЕНКА НАДЁЖНОСТИ ПРОГНОЗА В ТЕРМИНАХ ВЕРОЯТНОСТИ (Р). Значение надёжности прогноза является решением дифференциального уравнения надёжности. При любом заданном уровне строгости оценка надёжности (вероятность осуществления прогноза Р) варьирует от Р=0 (абсолютно ненадёжные области) до Р=1 (такой высокой надёжностью прогноза могут обладать лишь исходные популяции). Оценка надёжности меняется при изменении уровня строгости α: те объекты, надёжность которых приближается к максимальной (P≈1) при уровне строгости α=0.50. при переходе к более высокому уровню строгости α=0.90 будут оценены как менее надёжные (Р<<1).

КАРТЫ НАДЁЖНОСТИ

На картах надёжности интенсивность окраски соответствует степени достоверности картографического прогноза. Первый интервал (белый цвет) соответствует самой низкой оценке надёжности (Р<0.90). Второй интервал (0.90<Р<0.95) окрашен на черно-белых картах в светло-серые тона - надёжность приближается к достоверной, но не достигает традиционного для биологических исследований требования 95% уровня вероятности. Третий интервал (0.95<Р<0.975)- уже удовлетворительная оценка, поскольку вероятность выше 0.95; он окрашен в интенсивно серый цвет. Четвертый интервал (0.975<Р<0.99), окрашенный в темно-серый цвет, указывает на географическое положение высоко достоверных районов карты. Пятый балл (Р>0.99) соответствует наивысшей оценке надёжности (области исходных популяций) и окрашен на карте в самые интенсивные тона. Таким образом, повышение интенсивности цвета на карте надёжности соответствует увеличению надёжности картографирования.
При дальнейшем картографо-статистическом анализе надёжными считаются только те области карты, где вероятность правильного прогноза выше 95% (Р>0.95): только эти области распространения данного гена (или другой характеристики генофонда) учитываются при всех видах расчётов - корреляций, главных компонент, гетерозиготности и т. д.

КАРТЫ С УЧЕТОМ НАДЁЖНОСТИ

На картах признаков их значения показаны только в «надёжной» зоне, то есть для узлов ЦМ с вероятностью правильного картографического прогноза выше 0.95. В областях с меньшей надёжностью значения признака не приводятся («белые пятна» на карте данного признака).
Итак, «ненадёжные», то есть слабоизученные области, залиты на картах белым цветом и не используются в анализе, а все характеристики карты рассчитываются только по её надёжному пространству [Нурбаев, Балановская, 1997, 1998]. Число узлов карты (N), вошедших в «надёжное пространство» данного гена, указано в легенде каждой карты. Например, для ряда обобщённых карт русского генофонда N=1294. Это означает, что из 9000 узлов карты около 5000 узлов соответствуют ареалу других народов Восточной Европы, Кавказа и Урала, а остальные 2706 узлов русского ареала являются ненадёжными для данной системы признаков.
Таким образом, входными параметрами математической модели надёжности являются исходная геногеографическая карта (размещение опорных точек) и уровень строгости (а), выбранный для надёжности этой карты. Выходным параметром является вероятность прогноза (Р) значения признака в каждом узле исходной карты. Карты надёжности служат для отбора лишь тех точек картографического пространства, которые удовлетворяют требованиям надёжности.

§5. Простые преобразования простой карты

Мы уже говорили о том, что самые простые преобразования карты - это операции с отдельным узлом карты. Их проще всего представить, потому что такие операции проводятся с каждым узлом независимо.

СПЕКТР ПРОСТЫХ ПРЕОБРАЗОВАНИЙ

Статистическая трансформация отдельной карты осуществляется на уровне цифровой модели: с каждым значением матрицы ЦМ производятся операции, заданные тем или иным алгоритмом. В результате замены всех исходных значений матрицы преобразованными значениями создается новая - результирующая - ЦМ новой карты. К основным операциям по трансформации отдельной карты отнесены следующие: арифметические операции с константой (увеличение или уменьшение значений ЦМ на константу, умножение или деление на нее); возведение значений ЦМ в степень (положительную, отрицательную, целую, дробную); тригонометрические функции; логарифмические функции; перевод в абсолютные значения (взятие по модулю); дополнение до единицы. Эти операции комбинируются в любые сочетания, образуя цепочки многоступенчатых преобразований.
Трансформация отдельной карты широко используется при решении различных задач. Обычно такие преобразования являются промежуточными при сложных расчётах, однако они могут иметь и самостоятельное значение, например: при создании карты распределения частоты гена на основе карты альтернативного аллеля путем «вычитания карты» из единицы (1-q); при создании карты распределения гомозиготного генотипа на основе карты частоты аллеля путем возведения карты в степень (q²); при картографировании гетерозиготности и генетических расстояний двухаллель-ного локуса на основании карты частоты гена одного из аллелей; для различных нормализующих преобразований карты признака:

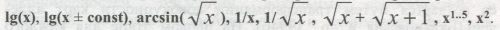
Статистическая трансформация совокупности карт проводится путем трансформации их ЦМ. Все трансформируемые карты обязательно должны быть построены на единой картографической основе и иметь одинаковое число узлов сетки с идентичной географической привязкой. Процедура преобразования состоит в следующем. Последовательно с Rij элементом каждой матрицы ЦМ (где i и j — координаты узла равномерной сетки) осуществляется заданная операция, результат которой после обработки всех исходных ЦМ заносится в соответствующий Rij элемент результирующей ЦМ. После повторения этой процедуры для каждого узла цифровой модели будет получена новая матрица ЦМ - результирующей карты.

Элементарные операции комбинируются в любые алгоритмы, включающие также трансформации отдельной карты. Методы статистической трансформации карт позволяют осуществлять переход от географии отдельного гена к основной цели и проблеме геногеографии - географии генофонда. Этот путь пролегает через промежуточные ступени: географию генотипов и географию важнейших показателей генетического разнообразия.

В качестве примера статистической трансформации совокупности карт рассмотрим создание карт гетерозиготности. что отчасти иллюстрирует как спектр возможных приложений, так и набор элементарных трансформаций.

СОЗДАНИЕ КАРТ ГЕТЕРОЗИГОТНОСТИ

Уровень гетерозиготности служит интегральным индикатором состояния генофонда: он реагирует на воздействия всех важнейших факторов микроэволюции - дрейфа генов, инбридинга, миграций, давления отбора, служит генетической компонентой продолжительности жизни [Алтухов, 1984, 1995, 1996, 1999; Livshits, Kobyliansky, 1984а,b; Kobyliansky, Livshits, 1983, 1986; Comuzzie, Crawford, 1990; Алтухов. Курбатова, 1990. 1993: Дуброва и др., 1988. 1990; Курбатова, 1996; Спицын и др., 19$6]. Величина среднего уровня гетерозиготности является важной характеристикой генофонда - есть основания полагать, что снижение или повышение гетерозиготности за пределы естественных флуктуации несет угрозу для генофонда. Однако при картографировании гетерозиготности возникают методические сложности: для нее нельзя прямо использовать интерполяционную процедуру, так как функциональная связь гетерозиготности популяций с их географическим ареалом сложнее, чем в случае частот генов.

Поясним это на примере. Пусть на картографируемой территории наблюдается тренд (градиент) частот генов, так что опорные популяции А1 и А5, территориально удалённые друг от друга, характеризуются следующими частотами гена: q_A1= 0.1; q_A5= 0.9. Тогда на карте в промежуточных точках А2, A3 и А4, лежащих на трансекте, проходящей через А1 и А5, интерполяционной процедурой задаются промежуточные значения частоты гена: _A2=0.3, _A3=05 и _A4=07

Поскольку гетерозиготность Н определяется через q: H=2q(l-q), то H_A1=0.18; H_A2=0.42; H_A3=0.50; H_A4=0.42; H_A5=0.18. Т.е. при ярко выраженном линейном градиенте частоты гена (q_A1=0.1; q_A3,=0.5; q_A5=0.9), значения гетерозиготности меняются нелинейно: в крайних точках они одинаково низки (H_A1=H_A5=0.18), а на промежуточной территории карты наблюдается повышение гетерозиготности до максимальных для двуаллельного локуса значений (H_A3=0.50). Если бы мы для получения карты гетерозиготности воспользовались непосредственно интерполяционной процедурой, то не сумели бы восстановить истинный рельеф гетерозиготности. В этом случае, поскольку в опорных популяциях А1 и А5 значения гетерозиготности одинаковы (H_A1=H_A5=0.18), вся карта гетерозиготности представляла бы собой унылую равнину: H_A1=0.18; H_A2=0.18 H_A3=0.18; H_A4=0.18; H_A5=0.18

Этот пример показывает, что геногеографические карты признаков, нелинейно-связанных с частотой гена и географическим пространством, нельзя получить прямым путем, интерполируя значения этих признаков: в этих случаях необходимо использовать трансформацию карт исходных признаков. Таким образом, единственный путь создания карт гетерозиготности - это трансформация карт частот генов.

Карта ожидаемой гетерозиготности полиаллельного локуса создается путем трансформации совокупности карт аллелей [Балановская и др., 19946]. На первом этапе для каждого аллеля создаются карты географического распределения его частоты (для всех аллелей - в одном и том же ареале, с одними параметрами построения карты и т. д.). Затем для каждого локуса рассчитываются карты гетерозиготности (Н) путем статистической трансформации карт аллелей локуса по алгоритму:

Согласно этому алгоритму с картами аллелей каждого локуса проводятся следующие трансформации: 1) значения ЦМ карты каждого аллеля возводятся в квадрат (карты распространения гомозиготных генотипов); 2) полученные карты суммируются в пределах локуса (карта гомозиготности локуса): 3) дополнение этой карты до 1 дает искомую карту ожидаемой гетерозиготности.
В результате такой многоступенчатой трансформации создаются карты пространственного распределения гетерозиготности для каждого локуса. Карта средней гетерозиготности по совокупности локусов получается с помощью двух последовательных трансформаций: 1) сложение карт гетерозиготности всех локусов; 2) деление суммарной карты на число локусов.
С помощью приведённых алгоритмов статистической трансформации можно получить геногеографические карты гетерозиготности любого генного локуса, карты средней гетерозиготности нескольких локусов или же генофонда в целом.
Важно подчеркнуть, что для систем сцепленных генов карты интегральной гетерозиготности могут отличаться от карт средней гетерозиготности не только по величине показателей, но и по их географии. Отметим, что обоснование преимуществ трансформации карт относится не только к гетерозиготам, но и в целом к картографированию генотипов.

§6. Карты корреляций и трендов

Карты корреляций и трендов относятся к следующему шагу по сложности преобразования - это операции, проводимые не с отдельным узлом карты, а с заданной группой узлов. Такие операции проводятся благодаря разработанной нами технике «плывущего окна». Эта техника позволяет решать многие сложные задачи анализа генофонда. Одним из многих, но наиболее часто используемым приложением метода «плывущего окна» является задача выявления трендов. Однако тренды можно выявлять и иным методом - моделирования с учетом всех узлов карты. Это уже третий шаг по сложности - операции со всеми узлами карты сразу. В этом разделе на примере карт трендов мы рассмотрим оба типа операций - и с группой узлов, и со всеми узлами карты. Так их будет проще сравнить.

ЧТО ТАКОЕ ТРЕНДЫ?

Геногеографическая карта отдельного гена может дать ответы на конкретные вопросы о распределении частоты гена по ареалу популяции, может служить для прогнозирования значений признака в генетически неизученных областях ареала, для планирования полевых исследований или же для решения других, не менее важных, но все же частных вопросов. Однако основное назначение геногеографической карты - выявление пространственных закономерностей. Такими закономерностями (трендами) могут быть и клинальная изменчивость (градиент значений признака), пронизывающая весь ареал генофонда; и некое ядро - центр влияния с расходящимися кругами убывающей интенсивности; и взаимопроникновение влияний нескольких центров; и пространственная динамика колебательного типа; или иные более сложные и комбинированные пространственные закономерности.
Они могут быть различны для разных признаков в одном и том же регионе. Но отличительными чертами пространственных закономерностей являются их объективность и устойчивость во времени и пространстве. Масштаб пространства и масштаб времени в общем случае соизмеримы. Чем крупнее ранг историко-географического региона, охваченного геногеографическим анализом, тем более глубокие и древние закономерности мы надеемся выявить. Однако карта доносит их до нас с наложившимися влияниями и воздействиями более поздних эпох.
Если представить географическую карту современного генофонда как совокупность наложенных друг на друга карт различных генетических эпох, тогда перед исследователем встает задача вычленения серии таких карт из суммарной, построенной на данных о ныне наблюдаемой генетической изменчивости. Наиболее простые способы решения этой задачи - для отдельной геногеографической карты -возможны в терминах вычленения трендовых (фоновых) поверхностей геногеографических карт, представленных в данном разделе.

КАК ОБНАРУЖИТЬ ТРЕНД?

Картографическое распределение (Z) признаков любой природы - экономических, геологических, демографических, биологических - можно рассматривать как картографическое воплощение совместного действия совокупности факторов. Одна их группа представляет основные, наиболее значимые и устойчивые факторы, обозначаемые как фоновые (Z_F), другая группа включает остаточные (Z_O), второстепенные воздействия. Они накладываются таким образом, что Z=Z_F+Z_O [Берлянт. 1986].

Если такую операцию подразделения Z на Z=Z_F и Z_O провести для каждого узла сетки ЦМ. то в результате получим две ЦМ новых карт: 1) фоновую ЦМ (Z_F), отражающую географию воздействия ведущих и длительно действующих факторов, сформировавших генетический рельеф; 2) остаточную ЦМ (Z_O), отражающую эфемерные явления. Эта ЦМ дополняет фоновую поверхность до исходной Z_O=Z-Z_F) и потому содержит как положительные, так и отрицательные значения.

Меняя параметры алгоритма, можно для одной и той же исходной карты получить серию фоновых поверхностей (Z_F1, Z_F2, Z_F3... Z_Fn), отражающих различные комплексы ведущих факторов. Построенная серия фоновых карт и будет представлять собою решение поставленной задачи: вычленения из суммарной карты (ныне наблюдаемой генетической изменчивости) её составляющих, отражающих разные эпохи и события. Каждая из карт этой серии несет информацию о тренде - основных пространственных закономерностях - определенного «стратиграфического пласта» генофонда. Глубина залегания этого пласта, степень его древности задаются параметрами построения фоновой картографической поверхности.
Мы приведем два наиболее универсальных способа получения фоновых карт - с помощью осреднения в «плывущем окне» (операции с группой узлов) и с помощью аппроксимирующей функции (операции со всеми узлами карты).

ТРЕНД В «ПЛЫВУЩЕМ ОКНЕ»

Вариантов получения фоновой карты методом осреднения немало - оно может проводиться вдоль определённых направлений или линий (например, параллелей или меридианов, рек или границ акваторий) или же для нескольких точек по границам ячейки определённых размеров (обычно по вершинам шестиугольника). Такие методы традиционны в картографии [Берлянт, 1969, 1986; Салищев, 1990]. Имея возможность получить компьютерное решение этой задачи, мы сочли более информативным осреднение не по линиям и точкам, а по площадям равномерно перемещающегося окна [Балановская, Нурбаев, 1995].

Разработанный метод получения трендовой поверхности с помощью осреднения в «плывущем окне» сводится к следующей процедуре. С помощью выбранного алгоритма вычисляется среднее значение для всех узлов ЦМ, находящихся на площади прямоугольника заданного размера. Результат осреднения присваивается центральной точке (узлу сетки ЦМ) прямоугольника. Затем прямоугольник перемещается на один шаг, равный расстоянию между узлами ЦМ, его центром становится соседний узел сетки ЦМ, и такая же процедура осреднения повторяется для него. После того, как для каждого узла сетки ЦМ повторена эта процедура и каждому узлу присвоены значения, средние по площади заданного прямоугольника, построение цифровой модели фоновой поверхности ЦМ (Z_F) окончено.
Остаточная поверхность вычисляется как разность между исходной и фоновой картами: ЦМ (Z_O)=ЦМ(Z)- ЦМ (Z_F).

«ПЛЫВУЩЕЕ ОКНО» ПОСТОЯННОГО РАЗМЕРА

Наиболее очевидным вариантом метода плывущего окна является осреднение в окне с размером, постоянным по всему ареалу генофонда [Балановская. Нурбаев, 1995]. В этом случае царит полное равноправие - все узлы фоновой карты в любой части ареала получают информацию от одинакового числа узлов исходной карты и в одинаковой мере стирают флуктуации, наслоившиеся на трендовую поверхность.
Основная задача, стоящая здесь перед исследователем, -подобрать такой размер окна, который отвечал бы цели работы: необходимости сохранения локальных особенностей процесса, сформировавшего генетический рельеф, или же воспроизведения лишь самых общих его тенденций. С увеличением размера окна - меняя масштаб осреднения - мы вскрываем всё более глубокие подстилающие пласты «генетической коры» и более устойчивые тенденции генетического процесса. Однако платой за это является потеря фоновой картой информации обо всех локальных особенностях генофонда.

Наиболее универсальным является размер окна, соответствующий среднему ареалу популяции при избранном масштабе исследования. Например, если нас интересуют закономерности, наиболее близкие к современности, или же мы исследуем внутреннюю структуру генофонда отдельного этноса, то целесообразно избрать окно осреднения, равное среднему ареалу элементарной популяции. При изучении генофондов крупных многонациональных регионов, при исследовании общих закономерностей их формирования, как бы снимающих отдельные события истории этноса, целесообразно использовать окно, равное среднему этническому ареалу. При изучении ведущих, глобальных закономерностей, сформировавших основные, подстилающие слои генофонда, можно использовать окна много больших размеров, соответствующих тем или иным надэтническим уровням популяционной иерархии.
В работе [Балановская. Нурбаев, 1995] для иллюстрации разных масштабов осреднения приведено исходное распределение частоты гена НР*1 в Северной Евразии и три фоновые поверхности, полученные из исходной с помощью плывущего окна постоянного - для узлов каждой карты размера. Окна осреднения соответствует площадям: «а» - 300x300 км: «б» - 900x900 км: «в» - 1500x1500 км. Различия между картами по степени обобщения генетической поверхности таковы. Карта с окном «а» в целом повторяет исходную карту, стирая «случайные черты» и облегчая её прочтение. При увеличении окна осреднения до «б» уже проявляются более глубоко лежащие закономерности. В основе генетического рельефа этой карты выявляется гряда высоких значений, широтно простирающаяся через весь субконтинент от запада до северо-востока и связанная с тремя пиками значений: северо-восточным; западносибирским: европейским. Как на север, так и на юг от гряды идет постепенное понижение генетического рельефа. В целом карта демонстрирует двухвекторный широтный тренд значений признака. Такое своеобразное широтное направление изолиний, возможно, отражает особенности разнонаправленного взаимодействия этого гена с факторами природной среды в северных и южных широтах.
При дальнейшем увеличении размеров плывущего окна - до «в» - сквозь широтную изменчивость начинает проявляться наиболее глубинная тенденция: долготный градиент значений частоты гена в направлении «запад - восток». Эта пространственная закономерность - долготного тренда - является ведущей при формировании генофонда Северной Евразии (с палеолитической эпохи). Она может рассматриваться как базисная при формировании и генетического рельефа гена НР*1. По аналогии с геологическими процессами её можно представить как направление наклона основной «глубинной» геологической платформы, на которую накладывается воздействие вторичных факторов, формирующих рельеф местности.
Выделить основные и вторичные факторы и тем более локализовать их географически, глядя на исходную карту, практически невозможно. Однако после их выявления методами фоновых карт, прочтение исходной карты приобретает большую научную глубину и объективность, позволяет обсуждать пространственную изменчивость признака в терминах закономерностей, тенденций, локальных особенностей и аномалий, позволяет подойти ближе к пониманию факторов, сформировавших структуру генетического рельефа.

Для большой наглядности для карт любых признаков обычно приводятся карты трендов, полученные при небольшом окне сглаживания случайных колебаний в частоте признака. В этом случае легенды самих трендовых карт обычно несут информацию о сглаженном рельефе, характеристики исходного генетического рельефа можно найти в таблицах.

«ПЛЫВУЩЕЕ ОКНО» МЕНЯЮЩЕГОСЯ РАЗМЕРА

Однако способ осреднения в постоянном окне имеет свои ограничения. Он эффективен при соблюдении двух условий - во-первых, равномерной изученности признака во всем картографируемом пространстве и. во-вторых, малой изменчивости размеров популяционных ареалов. Если нарушено хотя бы одно из этих условий, то осреднение в разных частях картографируемого пространства осуществляется как бы на разных уровнях обобщения.

Например, при использовании окна с размером, равным среднему этническому ареалу народов Северной Евразии, резкие различия в размерах этнических ареалов народов Сибири и народов Кавказа приведут к тому, что генетический рельеф Кавказа окажется в значительной мере стёртым. Осреднение для популяций Кавказа будет происходить не на уровне этносов, а на уровне лингвистических семей или даже более крупном, поскольку окно осреднения намного превышает этнический ареал народов Кавказа. В Сибири то же самое окно осреднения окажется меньше этнического ареала и недостаточным для устранения флуктуаций, возникающих в результате дрейфа генов и локальных миграций, поскольку осреднение будет происходить на субэтническом уровне организации. Подобная неравномерность осреднения приводит к неоднородности фоновой карты, поскольку в разных её частях оказываются отражёнными пласты различной древности, закономерности разных уровней обобщения.

Для устранения этих искажений нами специально разработан метод осреднения в «меняющемся окне» («Changing Window»): плывущее окно осреднения в разных частях картографируемого пространства принимает разные размеры в зависимости или от изученности признака, или от размера ареала популяции, или иных заданных параметров [Балановская, Нурбаев, 1995].

Чаще всего используется окно осреднения, меняющееся по картографируемому пространству в зависимости от числа опорных точек карты (популяций с исходной информацией), попадающих в окно осреднения. При построении фоновой поверхности распределения алгоритм осреднения учитывает следующие параметры [Балановская, Нурбаев, 1995]:

W_MIN - минимальный размер окна, с заранее заданным наименьшим числом узлов сетки карты.

W_MAX - максимальный размер окна. Размер окна (измеряемый в числе узлов сетки карты) не увеличивается больше W_MAX даже если в него не попало ни одной опорной точки.
К_OPT - заданное оптимальное число опорных точек, служащее пределом для увеличения окна.
f_K - функция зависимости веса значений признака от числа опорных точек в каждом из квадрантов окна (для этого окно подразделяется на четыре равных части - 4 квадранта). Эта функция определяет степень участия узлов сетки квадранта (в зависимости от их числа) при расчёте средней величины.
Процедура осреднения производится в следующем порядке. Начиная с минимального размера
W_MIN. окно осреднения увеличивается до тех пор, пока в него не попадает число опорных точек равное К_OPT. Если окно увеличилось до W_MAX, то даже если число опорных точек, попавших в окно, ещё не достигло К_OPT. окно перестает увеличиваться и проводится расчёт.

Затем проверяется, сколько опорных точек находится в каждом из квадрантов окна - чем больше точек в квадранте, тем больший вес придаётся значениям узлов сетки этого квадранта (в соответствии с функцией f_K) при расчёте среднего значения, которое присваивается центральной точке окна. Благодаря такой процедуре осреднения (повторенной для каждого узла сетки ЦМ), окно осреднения пропорционально популяционным ареалам и изученности картографируемого гена в различных областях картографируемого пространства. Благодаря различному весу квадрантов окна значения средних формируются по наиболее точным (наиболее обеспеченным опорными точками) областям окна.

В эффективности такого алгоритма легко убедиться при сравнении карты, полученной на его основе, с картами, полученными при плывущем окне постоянного размера. Это сравнение удобно тем, что оптимальное окно ожидается равным «б». W_MIN соответствует фоновой поверхности с окном «а». W_MAX соответствует фоновой поверхности с окном «в». В таблице 3.2. приведены статистические параметры сравниваемых карт: исходной карты распределения гена НР*1, трех карт с постоянным окном и карты с меняющимся окном (далее называемой CW -сокращенно от «Changing Window»).

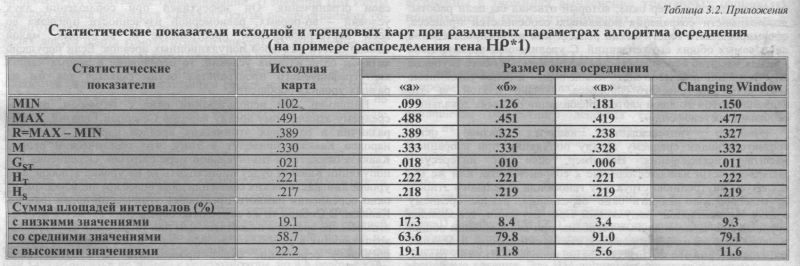
Практически по всем статистическим параметрам (табл. 3.2.) карты с CW наиболее близки к карте с постоянным окном осреднения «б», причём особенно важна близость показателей G_ST (G_ST(CW) = 0.11, G_STб = 0.010). Однако при практически одинаковом размахе изменчивости (R_CW = R_б = 0.33) минимальные значения частоты гена НР*1 на карте с меняющимся окном приближаются к значениям карты с окном «в», а максимальные - к показателям карты с окном «а». Это связано с различной обеспеченностью областей экстремумов исходными данными: области минимальных значений оказались слабо обеспечены исходными данными и потому менее надёжны и более интенсивно осредняются, чем области максимальных значений, надёжно обеспеченные для данного гена опорными данными и потому сохраняющиеся при методе меняющегося окна.

Генетический рельеф карты с CW в целом также наиболее близок к карте с постоянным окном осреднения «б». Однако карта с CW географически и исторически более точно воспроизводит границы ареалов тех или иных частот, поскольку ориентирована на фактический размер популяционного ареала и генетическую изученность народов. Карта CW отражает масштаб осреднения, связанный не с аморфным физическим пространством, а с историческим пространством, освоенным этносом.

Таким образом, метод «Changing Window» - осреднения в плывущем окне, размер которого меняется в зависимости от реального масштаба популяционного ареала и обеспеченности исходной информацией - позволяет даже в чрезвычайно гетерогенном регионе проводить осреднение во всех его частях на заданном уровне обобщения. Благодаря этому методу географическое пространство, вмещающее генофонд, перестает быть аморфным, однородным и нейтральным по отношению к структуре генофонда: при ориентации на реальный размер популяционного ареала в неявном виде учитываются природные и социальные барьеры на пути распространения генов. Возможность гибко изменять все четыре параметра окна осреднения (W_MIN, W_MAX, K_OPT, f_K) позволяет создавать серии картографических версий заданного уровня обобщения и тем самым как бы объемно моделировать генетический рельеф тех или иных исторических эпох.

ВЫЯВЛЕНИЕ ТРЕНДА АППРОКСИМИРУЮЩЕЙ ФУНКЦИЕЙ

Однако методы осреднения в окне - постоянного или меняющегося размера - «носят эмпирический характер и содержат элементы субъективизма» [Берлянт, 1986, с. 169]. Альтернативными считаются методы аппроксимации той или иной функцией, поскольку их модели опираются на строгий математический аппарат. При использовании аппроксимирующих функций фоновая и остаточная составляющие выделяются строго формально: аппроксимирующая функция описывает фоновую поверхность карты, отражающую искомые закономерности, а неучтенная часть соответствует остаточной компоненте [Берлянт, 1986]:

Z =f(u,v +Eps=Z_F+Z_O; f(u, v)=Z_F; Eps=Z_O.

Поставленной задаче - разделения фоновой и остаточной поверхностей - с математической точки зрения полностью соответствует математический аппарат разложения в ряды, в частности, ортогональные многочлены (полиномы) Чебышева. При их использовании фоновая поверхность представляет собой графическое изображение аппроксимирующего многочлена, сумма квадратов отклонений которого от фактической поверхности минимальна [Берлянт, 1986]. Но у математических моделей есть общий недостаток - простоте и четкости математического аппарата не всегда соответствует простота и ясность интерпретации.

В картографии, геологии, физике для аппроксимации принято использовать 1-й, 2-й и 3-й порядки ортогональных многочленов Чебышева, содержательная интерпретация которых наиболее очевидна. Согласно [Берлянт, 1986], каждой из этих моделей соответствуют определённые классы явлений, для которых они оптимальны. Аппроксимация многочленом 1-го порядка (Z_F1) моделирует моноклинальные поверхности, выявляющие направление сквозного градиента частот в распределении картографируемого признака и пронизывающие в едином направлении весь картографируемый ареал. Многочлены 2-го порядка (Z_F2) служат адекватной моделью для явлений, распространяющихся из единого центра с уменьшением градиента плотности признака во все стороны по мере удаления от центра. Многочленом 3-го порядка (_F3) наиболее оптимально аппроксимируется наложение двух различно ориентированных факторов или поверхности интерференции, создаваемой двумя центрами.

Фоновые поверхности, полученные из исходной поверхности рассмотренного выше распределения гена НР*1 с помощью ортогональных многочленов Чебышева, дали следующие результаты (эти же закономерности характерны практически для всех геногеографических карт) [Балановская, Нурбаев, 1995]. Аппроксимация многочленом:

1) 1-го порядка - моноклинальная изменчивость - позволяет определить направление общего наклона картографической поверхности данного гена. Эту карту можно интерпретировать как основной тренд гена, преобладающее направление общерегионального градиента частот.

2) 2-го порядка указывает расположение гипотетического центра распространения гена согласно модели эволюции из единого центра. Пик прогнозируемых значений значительно превосходит реально наблюдаемые пределы вариации аллеля.

3) 3-го порядка, т. е. в предположении наложения влияния двух центров, практически не отличается от предыдущей: ядро лишь несколько смещается в том или ином направлении.

4) более высоких порядков в географии, как правило, не используется. Объясняется это тем, что «содержательная интерпретация фоновых поверхностей, описываемых уравнениями четвертой и более высоких степеней, встречает затруднения» [Берлянт, 1986, с.173]. Видимо, это справедливо по отношению к несложным поверхностям, которые удовлетворительно описываются уже многочленом 2-го порядка [Берлянт, 1986]. Однако для геногеографических карт со сложным рельефом, сформировавшимся под действием многих, часто разнонаправленных и локальных факторов, использование более высоких степеней не только оправдано, но и необходимо. Компьютеризация процедур расчёта, усложняющихся пропорционально степени многочлена, позволяет построить аппроксимирующие поверхности любого порядка (необходимо лишь оборудование достаточно высокого класса, иначе построение карты высокой степени многочлена может занять несколько суток непрерывной работы компьютера).

В работе [Балановская, Нурбаев, 1995] приведены карты динамики прогнозируемого рельефа с ростом степени многочлена. Картина как бы постепенно уточняется, начинает учитывать локальные центры в изменчивости гена и от абстрактного указания на расположение источника распространения генов переходит к моделированию реального процесса его распространения. Поскольку величина порядка многочлена на единицу больше числа локальных экстремумов ряда, то можно предложить математически строгий критерий определения оптимальной степени многочлена. Его можно сформулировать следующим образом: степень оптимальной аппроксимирующей поверхности ортогонального многочлена Чебышева должна быть на единицу больше наблюдаемого числа локальных экстремумов исходной (аппроксимируемой) картографической поверхности. Многие особенности результирующей карты восстанавливают при этом реалии исходной карты распространения гена. Однако при этом карта моделирует потоки распространения гена из центров, независимых от внешних воздействий.
Таким образом, метод аппроксимации многочленами Чебышева позволяет подразделить фактическую поверхность и выделить её составляющие, различающиеся по происхождению. Первая составляющая (аппроксимируемая 1-й степенью многочлена и по определению не учитывающая локальные экстремумы) - это общий сквозной тренд моноклинальной изменчивости, пронизывающий весь ареал и объединяющий внешние воздействия на генофонд

- как природной, так и социальной среды. Вторая составляющая - это реконструкция центров, путей и направлений собственного саморазвития, независимого от внешнего мира: причём при высоких степенях многочлена эта составляющая реконструирует не только первичные, но и вторичные центры независимого развития.

ОСТАТОЧНАЯ ПОВЕРХНОСТЬ

Интересные результаты может дать и исследование остаточных поверхностей. Если остаточная поверхность отражает лишь случайные воздействия на генофонд, она мозаична и, как правило, малоинтересна. Однако она может зафиксировать и локальные аномалии в воздействии обших факторов, которые порой представляют не меньший интерес, чем сами закономерности. Сопоставляя фоновую и остаточную поверхности, можно обнаруживать области, отклоняющиеся от выявляемого тренда, и анализировать причины возникновения и важность тех или иных локальных особенностей в распределении того или иного гена. При обобщении остаточных поверхностей большой совокупности генов исчезает мозаичность случайных всплесков карты и появляется уникальная возможность обнаружить области аномалий в пространственной динамике генофонда в целом, указывающих на особенности его эволюции.
Таким образом, технология вычленения трендов позволяет на основе исходной геногеографической карты создавать серии трендовых (фоновых) карт и выявлять закономерности в пространственном распределении картографированного признака.

КОРРЕЛЯЦИОННЫЕ КАРТЫ

При исследовании пространственной изменчивости генофонда одной из важнейших задач является анализ связей между различными генами, между общими характеристиками генофонда (гетерозиготность, главные компоненты, дифференциация и т. д.), между параметрами генофонда и параметрами среды, культуры и т. д. Картографические технологии геногеографии создают целый спектр возможностей для количественного анализа пространственных связей.
Одним из инструментов является корреляционно-регрессионный анализ. В методы статистической трансформации карт входят алгоритмы расчёта различных показателей связей между геногеографическими картами: парной, ранговой, частной и множественной корреляции, коэффициентов регрессии. Для оценки связи между признаками рассчитываются корреляции между цифровыми моделями (ЦМ) карт соответствующих признаков. Чаще всего в геногеографии используются два показателя связи - коэффициент ранговой корреляции Спирмена и коэффициент частной корреляции [Айвазян и др., 1989]. Оба этих показателя, в отличие от наиболее известного коэффициента парной корреляции Пирсона, используются в тех случаях, когда необходимо определить взаимозависимость между рядами, распределенными не по нормальному закону (распределение частот аллелей в большинстве случаев отличается от нормального).
Для многих разделов, например, экологической генетики, чрезвычайно важно получить не общую на весь ареал оценку связи, а карту, которая позволяет видеть географию связи. Такая карта, показывающая тесноту связи на разных территориях, является уникальным инструментом для оценки пространственной изменчивости самих связей [Балановская. Нурбаев, 1999].
Традиционно исследователь использует для анализа единственный коэффициент корреляции на весь ареал. Такие «валовые» коэффициенты корреляции позволяют оценить степень связи в анализируемой системе в целом (например, степень связи между частотой гена и климатическими факторами среды, широтой и долготой местности [Spitsyn et al., 1998: Кравчук и др., 1998]). Однако гетерогенность среды и генофонда приводят к тому, что такая связь может различаться в различных частях ареала, причём не только по величине, но даже и по знаку. Поэтому наиболее полный и корректный анализ можно провести при картографировании самих корреляций, когда карта демонстрирует степень связи между анализируемыми параметрами в различных частях ареала.

Использование технологии «плывущего окна» позволяет создавать принципиально новые карты связей и зависимостей. В общем виде подход реализован нами следующим образом. На одной картографической основе строятся компьютерные интерполяционные карты всех анализируемых признаков (например, карта одного гена и карта средового параметра). Пункты изучения признаков не обязательно должны совпадать в пространстве, поскольку при переходе от исходных значений к карте интерполяция будет проведена на узлы густой равномерной сети. А уже сами картографические основы, сами сети карт должны быть идентичны. Далее используется процедура «плывущего окна»: в пределах части ареала («окна» заданного размера -постоянного или меняющегося) рассчитывается коэффициент корреляции (непараметрический), значение которого заносится в центральный узел «окна». Далее окно скользит на один узел, и вся процедура повторяется до тех пор, пока в каждый узел карты не будет занесено соответствующее ему значение корреляции. В результате этой процедуры получаем карту корреляций, демонстрирующую их гетерогенность в пространстве ареала. Размер окна (выбираемый в зависимости от задачи и масштаба исследований) может быть постоянным в пространстве карты, либо меняющимся, например, в зависимости от изученности частей ареала. Расчёт можно провести с учетом надёжности картографирования: части ареала с низкой достоверностью картографического прогноза не включаются в анализ корреляций.

Карта демонстрирует интенсивность связи в каждой точке пространства и позволяет анализировать пространственную изменчивость связей. Приведём распространённый пример. Коэффициент корреляции между картами двух признаков близок к 0. из чего делается вывод об отсутствии связи между признаками. Карта корреляций обнаруживает ошибочность этого вывода: половина ареала занята значениями корреляций r≈-1, другая половина - значениями r≈+1. и лишь узкий коридор между ними - промежуточными значениями r≈0. То есть карта обнаруживает не только высокую связь между признаками, но и её пространственную изменчивость: наличие двух областей с противоположным направлением связи, что позволяет искать факторы, определяющие взаимодействие признаков, формулировать гипотезы, которые можно проверять с помощью дальнейшего картографо-статистического анализа.
Таким образом, карты корреляций позволяют корректно анализировать связь как между параметрами среды и структурой популяции, так и между любыми другими признаками, гетерогенными в пространстве.
Корреляционные карты подразделяются на два основных типа: 1) картографирование связей между геногеографическими картами; 2) картографирование корреляций между картой частоты признака и географическими координатами местности - широтой и долготой.
В целом, в результате картографо-статистического корреляционного анализа создаются новые геногеографические карты закономерностей и связей, которые являются чрезвычайно чувствительным инструментом с большой разрешающей силой [Балановская, Нурбаев, 1999].

§7. «Синтетические» карты генетических расстояний

Карты изменчивости не одного признака, а сразу всей совокупности признаков, наиболее информативны при изучении закономерностей генофонда. Такие карты называют «синтетическими» или обобщёнными, поскольку они обобщают (синтезируют воедино) изменчивость многих отдельных признаков. Наиболее известны «синтетические» карты главных компонент - они служат основным инструментом изучения генофонда для коллектива Л. Л. Кавалли-Сфорца [Cavalli-Sforza et al., 1994]. В нашей картографической технологии реализован не один, а несколько подходов к созданию «синтетических» карт - не только главных компонент, но и карт общего генетического разнообразия, карт межпопуляционных генетических различий, карт гетерозиготности, а также карт генетических расстояний.
Наш опыт показывает, что наиболее объективным, мощным и вместе с тем наглядным вариантом «синтетических» карт являются карты генетических расстояний. Они позволяют формулировать и проверять гипотезы сходства и различий популяций. Ведь мы можем построить для одного и того же генофонда целую серию карт расстояний от самых разных популяций, как реальных (например, того или иного района, выделяющегося своеобразием, если мы хотим обнаружить генетические близкие ему популяции), так и обобщённых (начиная от обобщённых характеристик всего генофонда до характеристик самых разных его частей). В совокупности, вся серия карт генетических расстояний создаёт удивительно яркий и объёмный образ генофонда. При этом мы не являемся только созерцателями «портрета», а активно используем инструмент генетических расстояний, чтобы задавать генофонду все новые вопросы, получая всё более полные ответы.

ЧТО ТАКОЕ «КАРТА ГЕНЕТИЧЕСКИХ РАССТОЯНИЙ»?

Это карта, рассчитанная по совокупности множества карт разных генов. В каждом узле такой карты находятся не частота гена, а величина средней генетической удаленности данного узла сетки от той популяции, которая нас интересовала при создании данной карты генетических расстояний. Для этого рассчитываются многомерные расстояния (показатели генетических различий) от каждой популяции на изучаемой территории до генетических характеристик популяции, интересующей исследователя (так называемой «реперной» популяции). Соответственно, на карте каждая популяция присущим ей значением расстояний говорит о себе, насколько она генетически сходна с реперной популяцией. Например, если за реперную точку отсчёта взять обобщённую русскую популяцию, придав ей средние - по всем русским популяциям - значения частот признаков, то карта генетических расстояний покажет, насколько все русские популяции сходны или же отличны от среднеэтнических характеристик. Затем мы можем задать вопрос, а какие русские популяции и насколько близки к татарскому этносу? И тогда для тех же русских популяций мы рассчитаем их генетические расстояния до татар, а карта наглядно даст ответ на поставленный вопрос. Если в следующие карты мы включим не только русские, но и соседние популяции Восточной Европы, то значения расстояний будут показаны и для популяций иных народов. Тогда по карте можно сразу же увидеть, какие из них генетически наиболее близки к русскому или к татарскому генофонду.

АЛГОРИТМЫ

Для построения карт генетических расстояний наряду с традиционной и общеизвестной оценкой генетических расстояний по М. Nei [1975], нами используется алгоритм расчёта угловых расстояний Ѳ [Cavalli-Sforza, Edwards, 1967], где для локуса / с А аллелями:

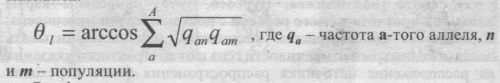
Эта функция привлекательна тем. что её квадрат пропорционален времени, потребовавшемуся на формирование генетического расстояния. Картографирование квадратов расстояний, таким образом, связывает географию генофонда со временем его развития. Для совокупности L локусов:

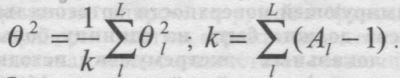
Этот несложный алгоритм позволяет создать карту с принципиально новым генетическим рельефом, обнаруживающим в терминах генетических расстояний близость либо отдалённость любых районов от заданных (реперных) значений: близости соответствуют низины, отдалённости - поднятия генетического рельефа, в какой бы части ареала они ни встречались. Для создания такой карты достаточно для каждого из аллелей локуса вместо q>m использовать реперную (например, средне региональную) частоту аллеля q, и провести для каждого узла сетки карты расчёт расстояний от локального значения признака в узле до средне-регионального:

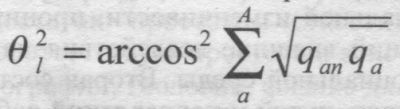
где q_a - константа, соответствующая заданному средне региональному значению частоты гена a; q_an - значение частоты гена а в п-ном узле (с координатами i,j) сетки карты, где п принимает значения от 1 до N (общего числа узлов карты).

Помещая каждое из полученных значений Θ² в соответствующий n-ный узел новой карты, мы картографируем генетические расстояния и получаем искомую карту генетической удаленности каждой из точек карты от реперных частот. Усреднением карт по всем анализируемым генам получаются средние карты генетических расстояний, которые и используются как окончательный результат анализа.

Располагая достаточно большой выборкой генов и популяций, можно с помощью описанного инструментария - картографирования генетических расстояний - исследовать историю генофонда в целом, обнаруживать генетические следы исторических событий [Рычков, Батсуурь, 1987; Рычков, Балановская, 1988; Балановская и др., 1997, 1998; Кравчук и др., 1998, Почешхова, 1998]. Принципиально важно, что, создавая серии карт генетических расстояний, мы можем последовательно формулировать и проверять гипотезы о сходстве и генетических различиях между любыми группами народонаселения. Это позволяет перейти от картографического моделирования к картографическому эксперименту и открывает чрезвычайно широкие перспективы для геногеографии. В целом, инструментарий генетических расстояний является много более мощным и перспективным, чем методы главных компонент, автокорреляций, «womblingw-анализа и другие, используемые ныне мировым научным сообществом для описания генофондов.

§8. «Синтетические» карты главных компонент

Карты главных компонент представлять не надо, как и их аналог для признаков с внутригрупповой корреляцией - канонические переменные. Эти методы уже давно стали традиционными как в антропологии, так и в генетике.

СУТЬ МЕТОДА ГЛАВНЫХ КОМПОНЕНТ

Метод главных компонент относится к группе методов снижения размерности, наряду с многомерным шкалированием, факторным анализом, анализом канонических переменных, методом экстремальной группировки признаков и другими [Айвазян и др., 1989]. Снижение размерности представляет собой переход от исходного набора многих показателей к небольшому числу вспомогательных переменных, на основании которых можно достаточно точно воспроизвести свойства анализируемого массива данных [Айвазян и др.. 1989].

Первой главной компонентой исследуемой системы показателей называется такая нормированно-центрированная линейная комбинация этих показателей, которая среди всех прочих нормированно-центрированных линейных комбинаций обладает наибольшей дисперсией. Любой k-той главной компонентой называется такая нормированно-центрированная линейная комбинация, которая некоррелирована с предыдущими главными компонентами и среди всех прочих нормированно-центрированных и некоррелированных с предыдущими линейными комбинациями обладает наибольшей дисперсией [Айвазян и др., 1989].

Главные компоненты обладают следующими основными свойствами [Айвазян и др., 1989; Дерябин, 2001]:
1. Первые главные компоненты характеризуются наибольшей информативностью, которая определяется величиной их дисперсии (долей от общей суммарной дисперсии всех исходных признаков).
2. Все главные компоненты нескоррелированы и поэтому представляют собой независимые признаки.

КАРТОГРАФИРОВАНИЕ ГЛАВНЫХ КОМПОНЕНТ

Геногеография позволяет не только провести стандартную процедуру анализа главных компонент, но и увидеть их распределение в географическом пространстве. Каждая из карт главных компонент отражает динамику новых обобщённых признаков генофонда, имеет свой генетический ландшафт и выдвигает на первый план особый исторический сценарий [Cavalli-Sforza, Piazza. 1993] развития генофонда. Карты главных компонент уже не раз публиковались и демонстрировались для самых разных генофондов - Восточной Европы, Европы, Евразии, мира [Menozzi et al., 1978: Ammerman, Cavalli-Sforza, 1984; Rendine et al., 1986; Рычков, Балановская 1992: Cavalli-Sforza et al.. 1995; Балановская, Нурбаев. 1997; Рычков и др.. 1997, 1998].

Основным стимулом для развития всей компьютерной геногеографии (как для зарубежной, так и для отечественной геногеографических школ) явилось именно стремление построить географические карты главных компонент. По мнению Л. Л. Кавалли-Сфорца [Cavalli-Sforza et al., 1994], построение карт главных компонент может облегчить визуализацию древних миграций, а также иные факторы, однотипно влияющие одновременно на целый ряд генов. Впервые карты главных компонент были созданы коллективом под руководством L. L. Cavalli-Sforza [Menozzi et al., 1978], причём для этого коллектива карты главных компонент («синтетические» карты) являются основным методом картографического обобщения [Menozzi et al., 1978; Piazza et al.. 1981 a,b; Ammerman, Cavalli-Sforza, 1984; Cavalli-Sforza et al.. 1995]. Независимо собственная технология картографирования главных компонент разрабатывалась одним из авторов (Е. В. Ба-лановской) в сотрудничестве с Ю. Г. Рычковым. С. М. Кошелем. Д. Б. Патрикеевым, Т. П. Папковой, С. Д. Нурбаевым. Последняя версия включает нормировку исходных данных, нормировку дисперсии, расчёт по корреляционной матрице и оптимизацию решения (упорядочивание собственных векторов и собственных чисел для обеспечения инвариантности решения). Основное отличие наших карт от создаваемых коллективом L. L. Cavalli-Sforza - в том, что наши карты обладают большей точностью и разработанностью деталей рельефа главных компонент (это связано с особенностями построения исходных карт генов). Однако по самой сути подхода и те, и другие карты главных компонент чрезвычайно сходны и могут сопоставляться без дополнительной коррекции.

Расчёт главных компонент осуществляется следующим образом. По значениям признаков (частот аллелей) в популяциях рассчитывается матрица корреляций всех аллелей друг с другом. Значения главных компонент для данной популяции вычисляются по значениям исходных признаков, умноженных на соответствующие коэффициенты. В качестве коэффициентов выступают собственные векторы ковариационной матрицы отдельных признаков, при условии некоррелированности получаемых на их основе главных компонент. Поэтому первым шагом является расчёт коэффициентов ковариации, затем производится решение соответствующего уравнения, корнями которого являются собственные вектора ковариационной матрицы, и, наконец, перемножением этих коэффициентов и значений частот аллелей находятся величины главных компонент.

Этот алгоритм расчёта главных компонент заложен практически во всех статистических программных пакетах. Поскольку в геногеографии необходимо провести расчёт карт главных компонент не по исходным данным, а по картам отдельных признаков, то для этого созданы оригинальные программы картографического пакета GGMAG. Так как цифровая модель карты представляет собой числовую матрицу со значениями частоты аллеля в каждом узле, то задача расчёта главных компонент сводится к получению значений главных компонент в каждом узле цифровой модели. При расчёте с использованием картографического пакета последовательность значений во всех узлах ЦМ выступает в том же качестве, как последовательность значений в одной строке таблицы данных при расчёте в обычном статистическом пакете. По данным во всех узлах ЦМ рассчитывается матрица корреляций всех ЦМ друг с другом. По корреляционной матрице вычисляются значения главных компонент для каждого из аналогов популяций (узлов равномерной сетки карты). Полученные значения главных компонент вновь присваиваются каждому узлу ЦМ. В результате создается ЦМ карт 1 главной компоненты, 2, 3 ... N главной компоненты, где N - число исходных карт отдельных признаков [Cavalli-Sforza et al., 1994; Балановская, Нурбаев. 1997]. Число результирующих карт главных компонент равняется числу исходных признаков, однако обычно рассматриваются карты только первых двух-трех компонент, описывающих основную часть изменчивости всех исходных признаков.

Таким образом, при расчёте карт главных компонент используется тот же алгоритм, что и при обычных статистических расчётах. Единственное отличие состоит в том. что получаемые значения главных компонент в популяциях (узлах сетки карты) имеют координатную привязку и поэтому представляются не в табличном формате, а в формате цифровой модели. Как указывалось, эта функция расчёта по значениям, привязанным к узлам ЦМ, реализована в программном пакете GGMAG.

ЗАЧЕМ НАДО СТРОИТЬ КАРТЫ ГЛАВНЫХ КОМПОНЕНТ?

Этот вопрос кажется простым - конечно, чтобы своими глазами увидеть невидимое - главные закономерности в изменчивости генофонда. Но на самом деле вопрос не так прост. Он подразумевает иное - а зачем надо разрабатывать сложные специальные программы? Почему геногео-графикам так важно строить карты главных компонент по исходным картам генов? Почему бы не рассчитать главные компоненты с помощью обычных статистических пакетов, а затем уже построить карты по полученным значениям главных компонент, как мы строим простые карты отдельных признаков? Иными словами, зачем так стараться создавать сложные карты, если можно построить простые? Особое значение, которое приобретает именно картографический, а не чисто статистический анализ главных компонент, объясняется в первую очередь неравномерностью исходных данных.

Неравномерность состоит в том, что по аутосомным генетическим маркёрам практически каждый локус изучен по собственному, отличающемуся от других, набору популяций. Это делает исходную информацию о генах несопоставимой и недоступной для прямого анализа главных компонент генофонда. Анализ главных компонент генофонда по исходным популяциям просто невозможен: большинство ячеек в матрице «популяции на гены» оказываются незаполненными, причём столь случайным образом, что из нее нельзя выбрать информацию, достаточно полно представляющую генофонд.

При изучении генофондов использование традиционного инструментария главных компонент наталкивается на почти непреодолимые трудности: необходимо, чтобы все популяции были изучены по одному и тому же набору генных маркёров. Однако (в отличие, например, от антропологии) программа генетических исследований не стандартизирована: практически каждый маркёр изучен по особому набору популяций. Требование унифицированности данных чрезвычайно сужает и набор популяций, и набор маркёров. Остаются два выхода: 1) ограничить число анализируемых популяций; 2) ограничить набор маркёров. Однако как несколько популяций не могут надёжно представлять всю популяционную систему, так и малый набор маркёров не может служить характеристикой генома в целом. При малом наборе популяций и маркёров анализ генофонда невозможен: анализируется случайный ряд популяций по нескольким генам, но не генофонд того или иного масшта- -ба. Именно поэтому, как правило, исходная информация о генах не позволяет широко использовать классический анализ главных компонент.

Выход из этой ситуации дает геногеография. Картографическая интерполяция помогает найти наиболее вероятные значения признака для тех точек карты и популяций, по которым исходная информация отсутствует. В результате заполняются «пробелы» вырожденной матрицы и появляется возможность включить в анализ главных компонент генофонда все изученные популяции и полный репрезентативный набор генных маркёров, в своей совокупности отражающие основные свойства и историю генофондов. Карты «надёжности» [Нурбаев, Балановская, 1997, 1998] позволяют выбрать из всей совокупности интерполированных значений лишь те, которые обладают высокой надёжностью. (Карты надёжности несут информацию о достоверности интерполированных значений признака в каждой точке картографируемого ареала, поэтому те области карты, которые не были обеспечены исходной информацией, не участвуют в анализе главных компонент.)

Например, изучение генофонда Восточной Европы опирается на генетическую информацию о 1586 популяциях, однако ни одна (!) из популяций не изучена по всему набору 30 локусов (100 аллелей). Практически каждый ген изучен по собственному, отличающемуся от других, набору популяций. Это делает исходную информацию о генах несопоставимой и недоступной для прямого анализа главных компонент генофонда.

Итак, единственный выход - это выход геногеографический: создать серию унифицированных карт. Причём карты каждого гена должны одновременно удовлетворять двум противоположным требованиям: с одной стороны, полностью учитывать всю исходную информацию о гене; а с другой стороны - быть полностью сопоставимыми с картами всех других генов.

На этих картах каждый узел их равномерной сетки является аналогом популяции. Для всей совокупности таких новых популяций (на картах генофонда Восточной Европы их около 9000) и по всей совокупности генов (карты 100 генов) рассчитываются главные компоненты - по стандартной по процедуре, описанной выше. Полученные значения главных компонент вновь присваиваются каждой из 9000 узлов сетки. Эта процедура стандартна и полностью соответствует привычному - не картографическому - анализу главных компонент. На основе 100 карт генов рассчитывается корреляционная матрица. Значения главных компонент рассчитываются для каждого узла равномерной сетки карты. В результате создается ЦМ карт 1, 2, 3 ... 100 компонент; благодаря нормировке и оптимизации решения среднее значение соответствующей компоненты равно нулю, дисперсия - единице, корреляция между картами компонент равна нулю. В результате анализа мы характеризуем аналоги популяций новыми признаками - главными компонентами, обобщающими информацию обо всех исходных признаках.

Отличие картографического анализа лишь в том, что самих популяций (узлов сетки) очень много, и они имеют строго упорядоченную географическую привязку. Благодаря этому мы можем, объединив значения главных компонент в интервалы и окрасив их (отрицательные значения - в светлые тона, положительные значения - в темные) увидеть своими глазами, как значения главных компонент распределены в пространстве. Таким образом, карты главных компонент представляют собой отображение трехмерного пространства: два измерения -географические, третье измерение - это генетический ландшафт главной компоненты. Обычно первые три компоненты вбирают в себя наибольшую часть общей дисперсии и как бы конденсируют в себе информацию об основных параметрах изменчивости наибольшей части генов.

КАК АНАЛИЗИРОВАТЬ КАРТЫ ГЛАВНЫХ КОМПОНЕНТ?

Далее можно изучать полученный генетический ландшафт главных компонент разными методами.

Во-первых, можно чисто качественно интерпретировать пространственные закономерности в терминах экологии или истории [Cavalli-Sforza et al.,, 1994; Рычков и др., 1997, 1999]. Но интерпретации могут быть разными. Главное в ином - мы выявляем объективно существующие пространственные закономерности всего генофонда, обнаруживаем «главные сценарии» в его изменчивости. Далее эти объективные закономерности могут поддаваться (или не поддаваться) той или иной интерпретации того или иного автора - важно, что есть реальный объект для обсуждения и выдвижения гипотез.

Во-вторых, выявленные картами главных компонент географические закономерности можно изучать количественно. Примером количественного изучения могут служить корреляции между картами главных компонент генофонда Европы и картами расселения земледельческого населения, материальной культуры палеолита, гетерозиготности, заболеваемости [Ammerman, Cavalli-Sforza, 1984; Cavalli-Sforza et al.,, 1994; Балановская и др., 1997; Рычков и др., 1998].

В-третьих, можно перейти к пространству главных компонент. Ведь на карте мы видим распределение аналогов популяций с определенными значениями главных компонент в географическом пространстве. Наша задача увидеть, как распределены эти популяции в самом пространстве главных компонент.

ПРОСТРАНСТВО ГЛАВНЫХ КОМПОНЕНТ

Мы говорили, что метод главных компонент может использоваться как в обычном статистическом, так и в картографическом обличье. И эти два подхода не изолированы: существует переход от карт главных компонент к обычному, статистическому представлению тех же результатов на графике.

Обычное представление главных компонент - двумерный график, по осям которого отложены значения главных компонент, а каждая изученная популяция представляется как точка на графике. Положение точки задаётся её координатами - значениями главных компонент в этой популяции. На таком двумерном графике популяции расположены в собственном пространстве - пространстве главных компонент. А на карте - эти же популяции представлены в реальном географическом пространстве. При картографическом представлении популяцией является узел цифровой модели, и для этой «картографической популяции» известно значение главной компоненты и её положение в географических координатах.

И обычное, и картографическое представление результатов являются двумерными, но в первом случае популяция характеризуется одновременно по значениям двух главных компонент и без указания географического положения, а во втором случае одна карта показывает значения только одной компоненты, зато представлена география. Итак, на двух картах представлена та же информация, что и на одном графике, плюс географическое измерение. И мы можем при желании отказаться от этого дополнительного измерения и «свернуть» две карты в один двумерный график.

Сделать это очень легко. Поскольку из карты первой компоненты известно значение компоненты для каждого узла карты, а из второй карты известны значения второй компоненты для тех же узлов, то каждый узел карты можно представить на обычном двумерном графике. Отличие такого графика пространства главных компонент, полученного через карты, от графика, полученного обычным статистическим путем, состоит только в числе и в географической равномерности точек-популяций: на картографическом графике их обычно сотни и тысячи - столько, сколько узлов в цифровой модели карты, в равномерной сети, покрывающей карту.

Несмотря на простоту такого графика, в процессе визуального анализа взаиморасположения изученных групп создается образ, несущий новую информацию о группах. В результате пространство главных компонент [Балановская, Нурбаев, 1997] становится важным инструментом для осмысления результатов, их критической интерпретации и сопоставления с информацией об истории и экологии изучаемых групп.

ЭТНИЧЕСКИЕ ОБЛАКА

При работе с картами возникает одна сложность. При обычном представлении мы опознаем каждую точку-популяцию по её номеру или названию, подписанному рядом с ней на графике. Но как назвать тысячи популяций, единственным «именем» которых являются их географические координаты? Для этого карта подразделяется на несколько зон, и узлы обозначаются особым значком в зависимости от того, в какую зону они входят. Этими зонами могут быть, например, ареалы народов, и такой приём позволяет обогатить график главных компонент новым содержанием. Если мы анализируем данные по нескольким народам, то на обычном графике главных компонент каждый народ будет представлен одной или немногими точками (изученными популяциями), а на графике, полученном через карты, каждый народ будет представлен целым облаком точек (узлов карты). Причём число точек в этническом облаке будет прямо соответствовать размеру этнического ареала. А компактность или же размытость этнического облака будет свидетельствовать соответственно о сходстве или же различиях разных популяций этого народа, то есть о большей или меньшей внутриэтнической гетерогенности.

Тем самым график главных компонент, построенный через карты главных компонент, показывает не только взаимное генетическое сходство изученных народов, но и степень популяционных различий внутри этих народов.

Как осуществить это технически? Процедуры и примеры их применения подробно описаны в [Балановская. Нурбаев, 1997]. Выделим на картах компонент ареалы интересующих нас этносов. А затем осуществим переход от географического пространства к пространству главных компонент следующим образом. Обозначим аналоги популяций - узлы сетки карты - в ареале каждого этноса значками единого цвета и формы. То есть цвет или значки будут выступать маркёрами этнической принадлежности популяций. Для каждого узла сетки считаем значения 1 и 2 компонент соответственно с ЦМ - цифровых матриц карт 1 и 2 компонент. Подчеркнём, что значения компонент считываются с ЦМ, а не с визуализированных карт: в ЦМ карты каждый аналог популяции -узел сетки - имеет математически строго определённое значение картографированного признака и не зависит от заданной шкалы интервалов. Разместим каждую популяцию в пространстве 1 и 2 главных компонент.

Количество точек - популяций - прямо пропорционально ареалу этноса. Популяции каждого этноса образуют как бы «этническое облако», причём «этническое облако» отражает межпопуляционную изменчивость этноса в пространстве главных компонент. «Центры тяжести» этнического облака соответствуют результатам традиционного - не картографического - анализа главных компонент, если бы этот анализ проводился по средним этническим частотам генов.

Важно отметить, насколько большую информацию мы получаем, используя всю картографическую информацию о разнообразии этноса, а не только положение в пространстве главных компонент этнических центров: различие в информативности «этнических облаков» (их размеров, положения, конфигурации, плотности и т. д.) и их «центров тяжести» соответствуют различиям в информативности картографического и традиционного анализа.

Этнические облака могут частично перекрываться. Такое перекрывание этнических облаков можно интерпретировать как генетическую близость. Возможны ситуации, когда этнические облака не перекрываются вовсе или же генофонд одного этноса размещён в пределах этнического облака другого этноса. К одним из наиболее важных преимуществ картографо-статистического анализа главных компонент следует отнести то, что этнос представлен в пространстве главных компонент не точкой, а всеми вариациями популяций в пределах этнического ареала. Компактность «этнического облака» свидетельствует о генетической однородности этноса, размытость границ - о неоднородности его генофонда. Поэтому для одних этносов «этническое облако» может сгущаться до состояния грозовой тучи, а для других - рассеиваться как перистые облака.

Важно подчеркнуть, что пространство главных компонент является не иллюстрацией, а важным элементом количественного анализа, поскольку положение популяций в этом пространстве адекватно отражает расстояния между популяциями. Причём «... геометрическое расстояние между любой парой популяций представляет собой «истинное» многомерное генетическое расстояние с наименьшей возможной ошибкой» [Cavalli-Sforza, Piazza, 1993, с.13]. (Хотя эта формулировка лучше соответствует другому методу снижения размерности - многомерного шкалирования -но в первом приближении может применяться и к графику главных компонент). Таким образом, благодаря пространству главных компонент, мы можем оценивать взаиморасположение популяций различных этносов, степень сходства и различий их генофондов, причём выражать эти сходство и различия в точных терминах генетических расстояний. Такая возможность - очень важное достоинство пространства главных компонент. Это означает, что визуальный образ, создаваемый пространством главных компонент, основан на математически точных пропорциях и соотношениях популяций.

Последнее замечание касается набора популяций. Поскольку в их качестве выступают узлы равномерной сетки, то весь ареал этноса представлен в пространстве главных компонент полностью и равномерно. Однако изученность этноса никогда не бывает равномерной: одни территории исследованы подробно, другие представляют собой белые пятна. Оценки частот генов для малоизученных территорий - лишь прогноз с определённой степенью надёжности. Это означает, что и значения главных компонент в разных частях ареала определены с разной степенью надёжности: для одних частей - они высоко достоверны, для других - имеют чисто прогностическое значение. Если у нас есть инструмент для оценки надёжности картографической информации, то мы можем оставить в «этническом облаке» лишь те популяции, в отношении которых информация достаточно достоверна. Эти диаграммы отражают «надёжное» пространство главных компонент в отличие от исходных диаграмм, отражающих «прогнозируемое» пространство главных компонент.

Сравнение «прогнозируемого» и «надёжного» пространства демонстрирует, какие популяции каждого из этнических облаков можно интерпретировать уверенно, а в отношении каких следует соблюдать осторожность. Важным выводом из сопоставления этих двух видов диаграмм является высокая устойчивость «центров тяжести» - средних этнических оценок главных компонент. В общих чертах все выводы, сделанные нами в отношении центров тяжести этнических генофондов и этнических облаков в целом при анализе прогнозируемого пространства, сохраняют свое значение при рассмотрении «надёжного» пространства главных компонент [см. Балановская, Нурбаев, 1997]. Лучше всего использовать одновременно обе диаграммы - «прогнозируемого» и «надёжного» пространства главных компонент: «прогнозируемое» пространство позволяет видеть этнос как целое в многообразии составляющих его популяций; «надёжное» пространство позволяет оставлять лишь те заключения, которые опираются на надёжно определённые популяции.

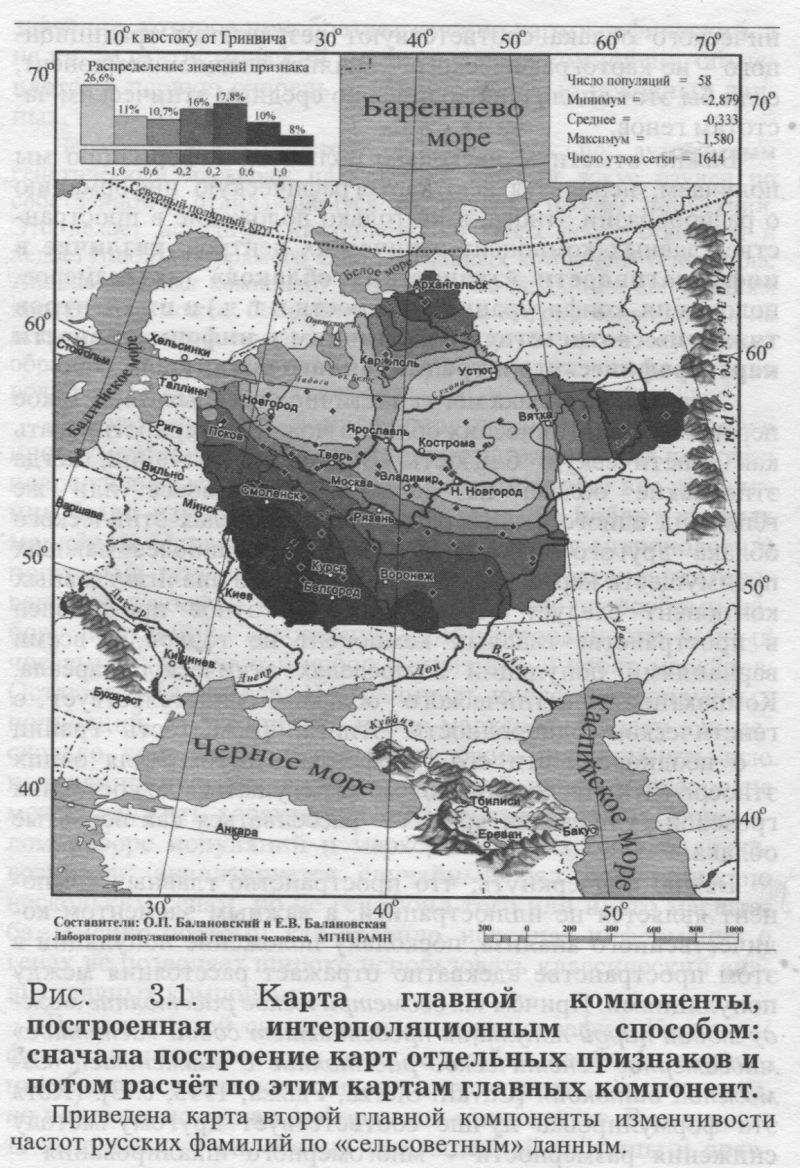
Карта главной компоненты, построенная интерполяционным способом: сначала построение карт отдельных признаков и потом расчёт по этим картам главных компонент.

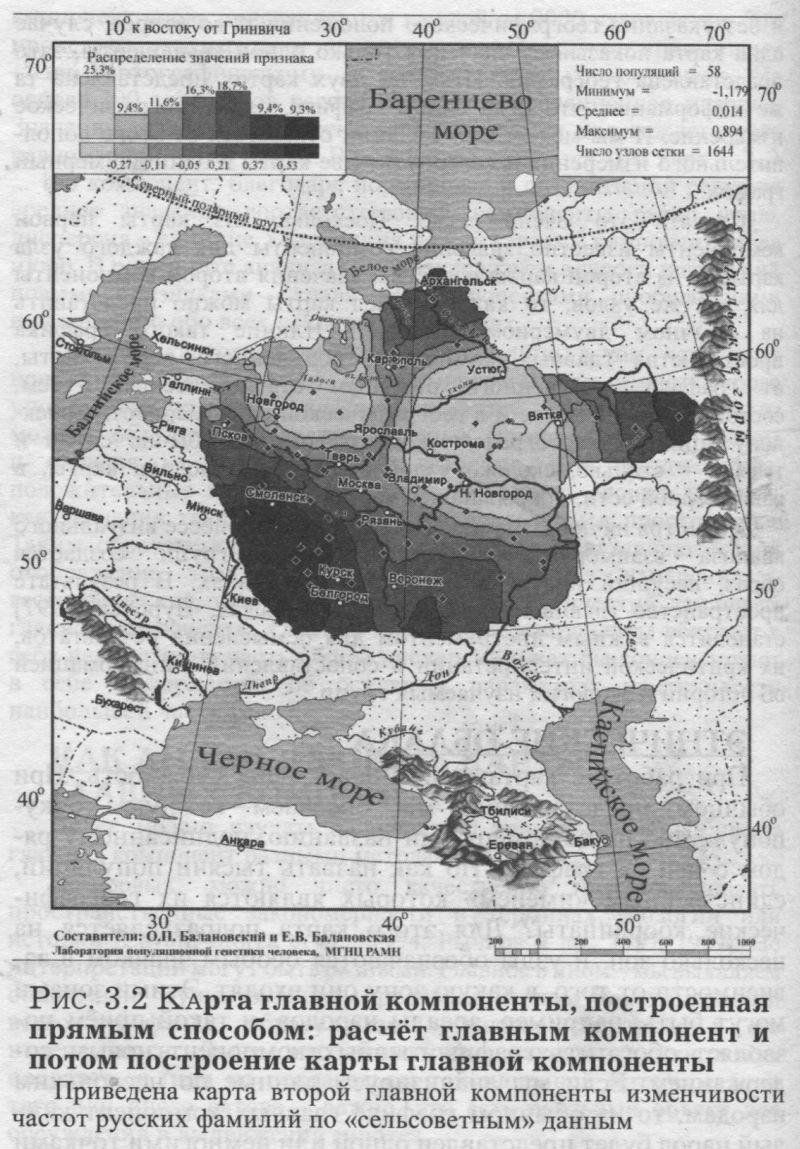
Карта главной компоненты, построенная прямым способом: расчёт главным компонент и потом построение карты главной компоненты

§9. Проблема ложных корреляций

В заключение коснемся важного методического вопроса, относящегося к картографированию главных компонент. Этот вопрос был очень остро поставлен в дискуссии между R. Sokal и L. L. Cavalli-Sforza об эффекте ложных корреляций, вносимых интерполяционной процедурой картографирования [Sokal et al., 1999ab; Rendine et al., 1999].

В чем же проблема? Поскольку число изученных популяций всегда много меньше числа узлов карты, при создании картографической модели необходимо использовать процедуру интерполяции данных. R. Sokal указывает, что это может привести к возникновению ложных корреляций между картами. Дело в том, что на территории промежуточной между изученными популяциями интерполяция прогнозирует постепенные изменения. И даже если в действительности картина более сложна, мы не сможем её выявить, пока не изучим промежуточные популяции, и наша карта будет «гладкой», с постепенными изменениями. Если теперь предположить, что постепенные изменения в данной области карты появятся на нескольких картах, то эти карты будут коррелировать друг с другом в данной области. Очевидно, что эта корреляция «индуцирована» интерполяцией и может иметь, а может и не иметь оснований в реальном распределении двух признаков. А так как главные компоненты вычисляются по матрице корреляций между картами, то и главные компоненты должны нести те или иные искажения вследствие ошибки таких ложных корреляций. Если же значения главных компонент были бы рассчитаны «прямым способом», то есть по исходным данным (без всяких карт), а уже потом по результатам такого расчёта построена карта главных компонент, то в этом случае, как указывает R. Sokal, мы избежали бы ошибки ложных корреляций. Вместе с тем R. Sokal согласен, что подобный способ расчёта (сначала рассчитать значения главных компонент, а потом уже картографировать «готовые» значения) возможен лишь в тех чрезвычайно редких случаях, когда весь ряд популяций изучен по всему набору признаков.

В целом, соглашаясь с логикой R. Sokal, мы считаем, что предложенный им выход - отказ от карт главных компонент -является мерой крайней и поспешной. Следует, по-видимому, провести более тщательное изучение этого вопроса - как теоретическое, так и путем прямого эксперимента. По аутосомным генетическим маркёрам провести такой эксперимент нельзя, так как нельзя построить карту главных компонент «прямым способом», поскольку популяции изучены по разному набору маркёров (в таблице «все популяции на все маркёры» многие ячейки пустуют). Однако квазигенетические маркёры (фамилии) и однородительские ДНК маркёры изучены обычно во всех популяциях (см. главы 6 и 7). Это позволило нам провести экспериментальную проверку значимости эффекта ложных корреляций.

ЭФФЕКТА ЛОЖНЫХ КОРРЕЛЯЦИЙ - НЕТ!

Итак, мы решили напрямую проверить - есть ли в действительности, а не в теории, эффект ложных корреляций?

РУССКИЕ ФАМИЛИИ. Для этого нами были построены карты главных компонент изменчивости русских фамилий в двух вариантах - расчёт «по картам» и расчёт «прямым способом». Во избежание всяких сомнений, эти карты были построены по популяциям строго одного уровня - по данным о частотах фамилий в сельсоветах. Рис. 3.1. демонстрирует результат первого способа расчёта («по картам»), вызвавшего сомнения R. Sokal (построение карт отдельных признаков и потом расчёт по этим картам главных компонент). На рис. 3.2. приведена карта этой же компоненты, но рассчитанная «прямым способом» и рассматриваемая как эталон правильности (расчёт главных компонент по исходным данным).
При сопоставлении этих карт становится очевидным их полное сходство. Коэффициент корреляции составил г=0.963. Это значит, что расчёт главных компонент «по картам» и «прямым способом» дал идентичные результаты.

ГАПЛОГРУППЫ Y ХРОМОСОМЫ В РУССКОМ ГЕНОФОНДЕ. Но, может быть, только фамилии обнаруживают столь полное совпадение? Нет. Мы провели полностью аналогичный анализ и для ДНК маркёров -изменчивости гаплогрупп Y хромосомы в историческом русском ареале. И вновь расчёт главных компонент «по картам» и «прямым способом» дал идентичные результаты: коэффициент корреляции составил r=0.997 [Balanovsky et al., 2008].

АДЫГЕЙСКИЕ ФАМИЛИИ. Такое же полное сходство (коэффициент корреляции составил r=0.98) мы обнаружили при сравнении расчёта главных компонент «по картам» и «прямым способом», проведённым по фамилиям иного народа - адыгейцев. Здесь важно не только то, что фамилии этого народа «говорят» на языке совсем другой лингвистической семьи и имеют много более древнюю историю и устойчивость. Для картографирования важнее иное - сам ареал адыгейцев имеет конфигурацию, альтернативную русскому ареалу. Если русский ареал един и компактен, то ареал адыгейцев он состоит из двух самостоятельных частей, разделённых Большим Кавказским хребтом. И, тем не менее, оба столь полярно различающиеся ареалы русского и адыгейского народа продемонстровали высочайшую степень сходства между картами главных компонент, полученными «по картам» и «прямым способом».

ВЫВОД Проведённые эксперименты показали, что метод вычисления главных компонент по интерполированным данным не приводит к ошибке «ложных корреляций».
Важно подчеркнуть, что при расчёте компонент учитывались лишь области с высокой достоверностью прогноза (р>0.95), полученные благодаря специальной технологии оценивания надёжности карт. Можно полагать, что именно включение в анализ только областей с высокой надёжностью важно для избавления от ложных корреляций.
Разумеется, требуются многочисленные исследования, чтобы выяснить границы применимости метода главных компонент в общем случае. Однако практически полное совпадение результатов, полученных «по картам» и «прямым способом» во всех трех случаях - русских фамилий, адыгейских фамилий и гаплогрупп Y хромосомы в русском ареале - указывает, что (при учете надёжности информации) результирующие карты главных компонент не содержат ошибки ложных корреляций.
Это позволяет утверждать, что обсуждаемые в данной книге карты главных компонент правомочны и отражают реальную картину пространственной изменчивости русского генофонда.

<<Назад Вперёд>>

Просмотров: 7284

загрузка...

Другие книги по данной тематике