§ 69. Начало развития теории строения атома; теория атома Бора

Имеет ли атом структуру или нет, состоит ли он из более мелких частиц материи или нет, является ли он истинно неделимым и т.д.,— эти вопросы спорадически возникали в истории науки и философии уже давно. Для многих ученых и философов прошлых веков атом представлялся действительно неделимым, не имеющим внутреннего строения. Однако были и такие, которые предлагали различные гипотезы о его строении. Уже Декарт и его последователи картезианцы атом рассматривали как частицу, образованную из материи, которая делится до бесконечности. Атомы, по Декарту, или, лучше сказать, частицы, из которых составлено вещество, могли изменяться по форме и по величине. Однако эта гипотеза вместе с общими представлениями Декарта о физических явлениях сравнительно быстро сошла со сцены.

В начале XIX в. мысль о сложном строении атомов высказал английский ученый Праут. Он исходил из результатов измерений, которые показали, что атомные веса элементов кратны атомному весу водорода. На основе этого Праут и высказал гипотезу, согласно которой атомы всех элементов состоят из атомов водорода.

В середине XIX в. с возрождением картезианских идей возникает гипотеза о том, что все атомы представляют собой особые образования в эфире. Такую гипотезу высказывал В. Томсон, который предлагает рассматривать атомы как вихревые кольца в эфире. Эти кольца, если рассматривать эфир как идеальную жидкость, не исчезают, они неделимы, между ними действуют силы, подобные молекулярным силам, и т. д.

Новый толчок для развития идеи о сложном строении атома дало открытие Дмитрием Ивановичем Менделеевым (1834—1907) периодического закона. Уже одно это открытие наталкивало на мысль о том, что атомы не являются неделимыми, что они обладают структурой и их нельзя считать первичными материальными образованиями. И действительно, вскоре появились новые гипотезы о строении атома. Так, например, английский химик и физик Крукс, опираясь на открытие Менделеева, высказал гипотезу о том, что все элементы образуются из некоего первоначального вещества, «протила», в результате его конденсации¹.

Дмитрий Иванович Менделеев

Открытие периодического закона Менделеева натолкнуло на идею о сложном строении атома Николая Александровича Морозова (1854—1946). Находясь в царской тюрьме, куда он был заключен за революционную деятельность в период 1886—1905 гг., не имея связи с внешним миром, Морозов разработал эту идею. Результаты своих исследований он смог опубликовать только после выхода из тюрьмы в 1907 г. Все атомы химических элементов, по Морозову, состоят из пяти основных частиц: трех частиц с атомными весами 1, 2, 4 (структурного водорода, протогелия и архония) и двух частиц электричества: отрицательной — «катодия» и положительной — «анодия». Все химические элементы в соответствии с его теорией являются сочетанием этих, как бы мы теперь сказали, элементарных частиц. Морозов предвосхитил ряд открытий в области химии и физики. Так, в его «катодии» нельзя не видеть прообраз электрона, об открытии которого он, конечно, не мог знать, находясь в заключении. Он писал:

«Когда я вводил «атомикулы» Катодия — К и Анодия — Аn в свои структурные формулы атомов, я делал это исключительно по теоретическим соображениям... В то время мне и в голову не приходило, что опытная физика уже стоит накануне одного из величайших открытий, которое должно было сразу преобразовать прежние представления об электрических явлениях как раз в том смысле, какой указывала для них моя теория.

Действительно, что такое мои Катодвй и Анодий? — Те самые отрицательные и положительные электроны, или электрические атомы, о которых теперь все говорят и пишут...»².

Попытка построить теорию строения атома на основе открытия Менделеева была предпринята также профессором Московского универснтета Б. Н. Чичериным в конце 80-х годов³. Анализируя свойства элементов с точки зрения периодического закона Менделеева, он выдвинул гипотезу о сложном строении атома. Атом, по Чичерину, подобен солнечной системе. Он состоит из центральной массы — ядра, вокруг которого вращаются периферические массы; между массами и ядром действуют силы притяжения, подобные силам тяготения.

«Каждый атом,— писал Чичерин,— представляет таким образом в бесконечно малом подобие солнечной системы, с центральною массою и обращающимися около нее телами. Самый закон тяготения в обоих случаях одинакий»⁴.

Теория строения атома, однако, начала по-настоящему развиваться только после открытия электрона и радиоактивности. Эти открытия совершенно определенно свидетельствовали о том, что атом нельзя считать неделимым и не имеющим внутреннего строения.

Первая гипотеза, первая модель атома, на основе новых открытий была разработана В. Томсоном и Дж. Дж. Томсоном. В наиболее законченном виде она была изложена последним в 1903 г. в книге «Электричество и материя»⁵.

Согласно этой модели, атом состоит из положительного заряда, равномерно заполняющего сферу, размеры которой имеют тот же порядок, что и атом. Внутри сферы находятся отрицательные заряды — «корпускулы» (термин «электрон» Томсон в данной работе еще не использовал), размеры которых гораздо меньше размеров сферы. Число корпускул в атоме велико. Так, по Томсону, самый малый атом, атом водорода, содержит около 1000 корпускул. Корпускулы внутри атома могут двигаться, например, вращаясь вокруг его центра, или находиться в покое. Дж. Дж. Томсон использовал оба представления при объяснении различных физических явлений, полагая, как и его знаменитый однофамилец В. Томсон, возможным пользоваться разными моделями одного и того же объекта. С помощью своей модели Дж. Дж. Томсон пытался объяснить многие физические и химические явления. Прежде всего Дж. Дж. Томсон показал, что его модель позволяет объяснить периодичность химических свойств элементов, выражаемую периодическим законом Менделеева. Оказывается, что при устойчивом состоянии атома электроны в нем должны располагаться концентрическими слоями с определенным числом электронов в каждом слое. С помощью предложенной модели Томсон объяснял линейчатый характер атомных структур, хотя спектральные закономерности ему объяснить не удалось. Он также объяснял проводимость металлов, считая, что атомы металлов легко теряют внешние электроны, которые становятся электронами проводимости. Дж. Дж. Томсон предполагал объяснить и явление радиоактивности, рассматривая атомы радиоактивных элементов как атомы, содержащие очень большое число электронов, которые вследствие постоянной потери энергии на излучение становятся неустойчивыми и распадаются (при этом выделяется энергия) и т. д.

Несмотря на то что уже вскоре была обнаружена ограниченность модели Томсона, она сыграла положительную роль в развитии теории строения атома. Из теории Томсона был заимствован ряд идей, и прежде всего идея о слоистом расположении электронов в атоме и объяснение на ее основании периодической системы элементов. Бор отмечал:

«... со времени знаменитой попытки Дж. Дж. Томсона истолковать периодическую систему на основании исследования 1 устойчивости различных электронных конфигураций идея о разделении электронов в атоме на группы стала исходным пунктом и более новых воззрений. Предположение Томсона о распределении положительного заряда в атоме оказалось несовместимым с опытными результатами, полученными на основании изучения радиоактивных веществ. Тем не менее эта работа содержит много оригинальных мыслей и оказала большое влияние на дальнейшее развитие атомной теории»⁶.

Эрнест Резерфорд

Японский физик Нагаока в 1904 г. предложил планетарную модель атома⁷. По этой модели атом состоит из положительного ядра, вокруг которого вращается кольцо, состоящее из большого числа электронов. Однако такая гипотеза не привлекла серьезного внимания.

В 1905 г. в докладе на 77-м съезде немецких естествоиспытателей и врачей вопроса о планетарной модели атома коснулся Вин⁸. Он высказался против такой модели, поскольку атом, построенный согласно ей, не может быть устойчивым, вследствие того что электроны в таком атоме должны излучать и быстро терять энергию.

В 1909—1910 гг. сотрудниками лаборатории английского физика Эрнеста Резерфорда (1871—1937) были проведены экспериментальные исследования рассеяния α-частиц тонким слоем вещества. Эти исследования показали, что для большинства α-частиц, пронизывающих тонкий слой вещества, можно принять, что они рассеиваются силовыми центрами, которые действуют на них с силой, обратно пропорциональной квадрату расстояния. Для некоторых же сравнительно немногих частиц, отклонение которых составляло угол 90° и больше, нужно было принять, что они встретились с очень сильными электрическими полями (в результате они даже отбрасываются назад).

Анализируя данные эксперимента, Резерфорд был вынужден в 1911 г. в работе «Рассеяние α- и β-частиц веществом и строение атома» высказаться за планетарную модель атома. По теории Резерфорда⁹, атом состоит из положительного ядра, гораздо меньших размеров, нежели атом, порядка 10^-13 см. Вокруг ядра вращаются электроны. Общий заряд атома равен нулю, поэтому заряд ядра по абсолютной величине равен ne, где n — число электронов в атоме, е — заряд электрона. Резерфорд полагает в согласии с мнением ван ден Брука, высказанным ранее, что число электронов в атоме должно быть равно порядковому номеру элемента в периодической системе Менделеева.

Модель атома Резерфорда, казалось, совершенно определенно следовала непосредственно из экспериментов. Однако несмотря на это, против нее можно было выдвинуть те же возражения, которые были высказаны Вином против планетарной модели. Кроме того, данная модель не могла объяснить вид атомных спектров, при изучении которых уже была установлена определенная закономерность в распределении спектральных линий. Уже в 1885 г. Бальмер установил, что длина волн спектра водорода в видимой части в трубке Гейсслера выражается простым законом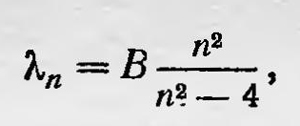

где В — некоторая постоянная; n — целое число, большее двух.

Через несколько лет Ридберг установил, что подобный закон существует и для атомных спектров некоторых других элементов. На основании экспериментальных исследований он показал, что в спектрах этих элементов существуют серии, длины волн которых определяются формулой

1/λ = А — R/(n + α)²,

где А и α — определенные постоянные, характерные для каждой серии; R — постоянная, названная постоянной Ридберга.

В дальнейшем было исследовано распределение спектральных линий водорода в ультрафиолетовой и инфракрасной областях и получена общая формула для спектра водорода:

1/λ = R (1/n² — 1/m²),

где m и n — целые числа.

Наконец, Ридберг и Ритц, обобщая результаты исследований спектров, пришли к выводу, что длина волн спектральных линий атомов различных элементов может быть представлена формулой

1/λ = Т'(n) — Т"(m).

Таким образом, определенным сочетаниям Т’(n) и Т"(m) соответствует определенная спектральная линия. Это положение получило название комбинационного принципа Ритца. Но модель атома Резерфорда никак не могла объяснить такой характер атомных спектральных закономерностей. Таким образом, проблему строения атома нельзя было считать решенной.

В 1913 г. Томсон, учтя экспериментальные данные по рассеянию α-частиц и соображения Резерфорда, разработал новую модель атома¹⁰. Теперь он предположил, что атом состоит из ядра малых размеров, вокруг которого расположены электроны. Но сила взаимодействия между электронами и ядром уже не является кулоновской, а зависит от расстояния по следующему закону: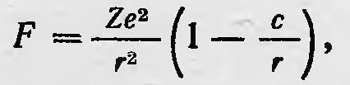

тде с — постоянная (по порядку величины она равна 10^-8 см).

В случае действия такой силы электроны в атоме могут находиться в равновесии, будучи неподвижными. Так, например, если в атоме один электрон, то он находится в равновесии на расстоянии ∼10^-8см от ядра. В случае многих электронов условие устойчивого равновесия усложняется. В этом случае электроны при равновесии должны располагаться вокруг ядра в виде колец, аналогично тому, как это было в первой модели Томсона. Будучи выведен из положения равновесия, какой-нибудь электрон начинает совершать внутри атома периодическое движение, если полученная им энергия не превышает определенной величины. Если же эта энергия превышает некоторую критическую величину то электрон покинет атом. В последующем Томсон усложнил свою модель. Он предположил, что сила взаимодействия между электроном и ядром зависит не только от расстояния, но и от ориентации электрона относительно ядра в пространстве, т. е. что она не обладает сферической симметрией. С помощью новой модели Томсон пытался объяснить не только опыты Резерфорда, но и спектральные закономерности, и дискретный характер излучения и поглощения энергии атомом, и целый ряд других физических, а также химических явлений. Томсон довольно долго придерживался своей новой гипотезы строения атома. Даже в 1923 г., когда уже общепризнанный среди физиков стал ас теория Бора, Томсон в своих лекциях излагал указанную модель и применял ее для объяснения многих физических и химических явлений¹¹.

Появились и другие работы, в которых высказывались новые гипотезы о строении атома, отличные и от гипотез Резерфорда и Томсона. В этих работах, например, предполагалось, что атомное ядро обладает магнитным моментом, вводились гипотезы о том, что внутри атома пространство обладает отрицательной кривизной, и т. д. Однако все эти гипотезы носили искусственный характер¹² и не имели успеха.

Успеха в построении теории атома добился в 1913 г. молодой датский физик Нильс Бор (1885—1962), работавший в лаборатории Резерфорда. Бор понял, что для построения теории, которая объясняла бы и результаты опытов по рассеянию α-частиц, и устойчивость атома, и сериальные закономерности, и ряд других экспериментальных данных, нужно отказаться от некоторых принципов классической физики.

Нильс Бор

Можно взять за основу модель атома Резерфорда, но дополнить ее новыми гипотезами, которые не следуют или даже противоречат классическим представлениям. Эти гипотезы известны как постулаты Бора. Они сводятся к следующему. Каждый электрон в атоме может совершать устойчивое орбитальное движение по определенным орбитам, с определенным значением энергии, не испуская и не поглощая электромагнитного излучения. Электрон способен перескакивать с одной стационарной орбиты на другую, и только в этом случае он испускает или поглощает определенную порцию энергии монохроматического излучения определенной частоты. Эта частота определяется величиной изменения энергии атома при таком перескоке в согласии с теорией Планка. Именно, если при переходе электрона с орбиты т на орбиту п энергия атома изменяется от Е_m до Е_n, то испускаемая или поглощаемая частота определяется условием

hv_mn=E_m-E_n,

Эти гипотезы (постулаты) Бор использует для расчета простейшего атома (атома водорода), рассматривая первоначально наиболее простую его модель: неподвижное ядро, вокруг которого вращается по круговой орбите электрон. Возникает вопрос, какие же орбиты атома водорода стационарные? Для его решения Бор выдвигает предположение, что стационарными являются орбиты, для которых удовлетворяется соотношение Е =hn ω/2, где E — абсолютное значение энергии электрона на данной орбите, ω — частота обращения электрона на ней, a k — целое число. Как сам позже писал Бор¹³, эта гипотеза возникла по аналогии с гипотезой Планка о том, что энергия осциллятора В может иметь значение Е = khv. Но у осциллятора средние значения кинетической и потенциальной энергии равны. Таким образом, на средние значения только кинетической энергии приходится Е_K=1/2 khv. Отсюда Бор предположил, что для кинетической энергии (и энергии вообще) электрона в атоме водорода должно существовать соотношение E=k½hω. Приняв эту гипотезу, Бор подсчитал выражение энергии электрона в атоме водорода для стационарных орбит: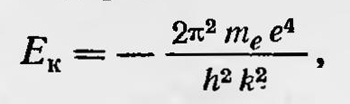

где m_e — масса электрона, е — его заряд.

Для частот, излучаемых атомом водорода, получаем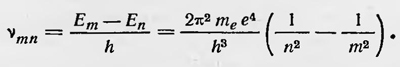

Полученное выражение совпадает с приведенной выше эмпирической формулой, и вычисленное значение ѵ_mn хорошо подтверждается данными измерений.

Объяснение спектра водорода было большим успехом теории Бора. Прямым ее подтверждением были результаты опытов Франка и Герца по исследованию возбуждения и ионизации паров ртути ударами электронов, проделанных в 1914 г. В опытах Франка и Герца было показано, что удары электронов об атомы ртути, если энергия первых меньше некоторого критического значения Е_n являются упругими. Когда же их энергия достигает этого значения, то удары становятся неупругими, энергия электронов полностью передается атомам ртути, они возбуждаются и начинают излучать. Частота излучения равна E₁/h. При дальнейшем увеличении энергии электронов удары опять становятся упругими, и только при достижении определенных значений Е₂, Е₃, ... энергия во время соударения вновь целиком передается атомам ртути, которые, возбуждаясь, излучают определенные спектральные частоты. Опыты, проведенные с другими элементами, показали, что и для них наблюдалась такая же закономерность. При соударении электронов с атомами последние способны воспринимать только определенные количества энергии Е и излучать определенные частоты.

Таким образом,опыты Франка и Герца непосредственно подтверждали и предположение Бора о существовании особых стационарных состояний атома, и предположение о том, что частота электромагнитного излучения атома определяется изменением его энергии при переходе из одного стационарного состояния в другое в соответствии с условием

hv_mn=E_m-E_n.

Дальнейшее развитие теории Бора происходило прежде всего в направлении поисков более общих условий, определяющих стационарные состояния атомов. Как мы видели, сначала Бор принял орбиты электрона круговыми и ввел для определения энергии, а также радиуса стационарных круговых орбит условие E_k = k½hω, которое можно записать иначе. Если ввесви в рассмотрение момент импульса электрона М, то получим πМ=Т/ω, где Т — кинетическая энергия электрона. В случае круговых орбит, для которых абсолютное значение Е = Т, имеем

M=k h/2π,

ли М = kM₀, если ввести постоянную величину M₀=h/2π. Это условие можно распространить не только на круговые орбиты, оно явилось первым обобщением квантового условия.

В 1915 г. независимо друг от друга Зоммерфельд и Вильсон ввели более общие квантовые условия, которые были применены к атому водорода. Дальнейшее обобщение этих условий было проведено Шварцшильдом и Эпштейном. Условия эти относились к системам со многими степенями свободы, совершающим такие движения, когда можно выбрать обобщенные координаты q_i, периодически изменяющиеся в интервалах между постоянными значениями q'_i и q"_i. Для таких систем условием стационарности является условие кратности интегралов ɸ p_i dq_i постоянной Планка h, где p_i — обобщенные импульсы, т. е. условие

ɸP_i dq_i — kh,

где k — целое число.

Использование более общих условий квантования позволило более точно рассчитать энергетические уровни атома водорода с учетом эллиптических орбит электрона и даже релятивистских поправок, а также рассчитать энергетический спектр атома водорода в магнитном и электрических полях, т. е. эффект Зеемана и эффект Штарка.

В общем случае электрон в атоме водорода обладает тремя степенями свободы, поэтому для определения орбит электрона нужно принять во внимание три квантовых условия. Если положить, что ядро атома покоится, и ввести сферические координаты, то эти три условия можно записать в виде

ɸp_r=n_rh, ɸp_ϑdϑ=n_ϑh, ɸp_ψdψ=n_ψh

где r, ϑ, ψ — сферические координаты, p_r, p_ϑ, p_ψ — соответствующие импульсы, а n_r, n_ϑ и n_ψ — целые числа.

Однако если внешние магнитное и электрическое поля отсутствуют, то можно ограничиться двумя условиями квантования, рассматривая движение электрона как движение с двумя степенями свободы. В этом случае можно ввести полярную систему координат (r, φ). Тогда условия квантования следующие:

ɸp_rdr=n_rh, ɸp_φdr=n_φh.

Расчеты показали, что энергия Е и момент количества движения электрона для стационарных орбит выражаются так: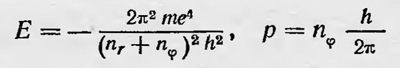

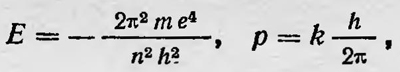
где п=n_r + n_φ — главное квантовое число, определяющее значение энергии электрона на соответствующей орбите; k — азимутальное квантовое число, определяющее его момент импульса или вид эллипса данной орбиты. Отсюда видно, что при данном главном квантовом числе п азимутальное квантовое число может принимать n значений k = 1, 2, 3, ..., n.

Более строгая теория атома водорода для нерелятивистского случая мало что добавляет к теории Бора, изложенной им в первой работе. Она давала те же значения, энергии для стационарных состояний атома, а значит указывала на те же спектральные линии, что и последняя. Для более сложных случаев, однако, теория Зоммерфельда приводила к новым результатам и являлась дальнейшим шагом в развитии теории атома. Во-первых, Зоммерфельд применил эту теорию для расчета возможных энергетических состояний атома водорода, учитывая релятивистские эффекты, т. е. зависимость массы электрона от скорости движения по орбите. В этом случае орбита электрона не является строго эллиптической, а имеет вид розетки, образованной вращающимся эллипсом, у которого большая полуось совершает медленный поворот в плоскости орбиты. Возможные значения энергии атома водорода в данном случае в первом приближении равны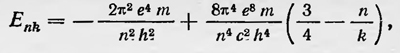

т. е. определяются не только главным квантовым числом n, но и квантовым числом k. Следовательно, спектральные линии водорода должны представлять собой группы близких линий (так как второй член в выражении для E_nk гораздо меньше первого), образуя так называемую тонкую структуру. Экспериментальные исследования подтверждали наличие тонкой структуры в спектре водорода.

В 1916 г. Зоммерфельд, а также Дебай применили квантовые условия для теории эффекта Зеемана. В этом случае нужно использовать сферические координаты и все три условия квантования.

Расчет показывает, что энергия атома водорода, помещенного в магнитное поле, определяется двумя квантовыми числами n и m равна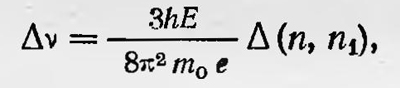

где Н — напряженность магнитного поля; m₀ — масса электрона, а n и m — квантовые числа; n — по-прежнему главное квантовое число, которое полностью определяет энергию атома при отсутствии магнитного поля; m — новое квантовое число, которое появляется в результате квантового условия для координаты ψ:

ɸp_ψdψ=n_ψh=mh.

Здесь p_ψ является моментом импульса, соответствующего координате ψ, и имеет простой смысл. Именно: p_ψ, — проекция момента импульса электрона на направление напряженности магнитного поля. Таким образом, общая энергия электрона в данном случае зависит от ориентации его орбиты в пространстве относительно направления магнитного поля. Здесь имеет место случай так называемого пространственного квантования. Частота спектральных линии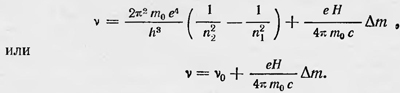

Полученный результат согласовался с экспериментом (для случая нормального эффекта Зеемана), если принять, что Δm= -1,0,+1, т. е. что m либо не изменяется, либо изменяется на единицу. Почему это так, было неясным, что указывало на какой-то недостаток теории, на необходимость новых ее дополнений.

Условия квантования были применены также для расчета открытого Штарком эффекта расщепления спектральных линий в электрическом поле. Этот расчет был сделан в том же 1916 г. Шварцшильдом и Эпштейном. Им пришлось ввести параболическую систему координат и записать выражение для условия квантования в этой системе, введя соответствующие квантовые числа.

Для энергии атома в электрическом поле они получили выражение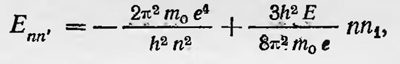

где Е — напряженность электрического поля, n — главное квантовое число, n₁ — новое квантовое число, Которое может принимать значения n — 1, ..., —1, 0, +1, ..., n — 1.

Таким образом, спектральные линии водорода расщепляются на ряд линий, отличающихся от первоначальных на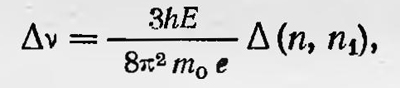

что подтверждается экспериментом.

После первых результатов, достигнутых в теории строения атома водорода и объяснения на основании этой теории спектров, были предприняты шаги в развитии теории строения более сложных атомов и объяснений структуры их спектров. В этом направлении были достигнуты некоторые успехи, однако исследователи встретились с большими трудностями. Помимо этого, встал вопрос о возможности расчета интенсивностей спектральных линий, а также задача дать объяснение, почему не все спектральные линии, предсказываемые теорией, в действительности наблюдаются в исследуемых спектрах. Почему, например, в эффекте Зеемана присутствуют спектральные линии, для которых квантовое число m либо совсем не меняется, либо изменяется только на ±1. Это так называемое правило отбора нужно было как-то оправдать. Появились и другие правила отбора, устанавливающие, какие энергетические переходы из всех мысленно возможных осуществляются в действительности. Как, например, объяснить установленный факт, что квантовое число k может изменяться на ±1 и т. д.? Для решения подобных вопросов Бор использовал так называемый принцип соответствия, который первоначально иногда называли также принципом аналогии. В основе этого принципа лежит представление о том, что хотя между квантовым и классическим представлениями о процессе излучения атома имеется коренное различие, тем не менее между ними можно усмотреть определенную математическую аналогию.

Первоначально Бор сформулировал принцип соответствия для простого случая атома водорода¹³. Пусть электрон в атоме водорода находится на стационарной орбите с главным квантовым числом n. Тогда число обращений электрона на орбите в одну секунду ѵ_кв = 2π²me⁴/(h³n³) или, вводя постоянную Ридберга R, ѵ_квв = 2R/n². По классической теории, этот атом должен излучать спектр частот ѵ_кл= ѵ, 2ѵ, Зѵ.....При этом интенсивность излучения частот можно определить, разложив движение электрона в ряд Фурье. Например, для одной из координат

где τ — целое положительное число.

Но согласно теории Бора атом, находящийся в этом состоянии, излучает не во время движения электрона по орбите, а при переходе его с орбиты n на другие орбиты с меньшим квантовым числом n^{1/sup>. При этом частота излучения

ѵ_кв=R(1/n^{1/sup>²-1/n²).

Пусть теперь n и n^{1/sup> — большие числа, а их разность n — n^{1/sup> мала по сравнению c их значениями; тогда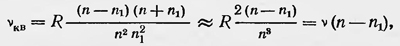

т. е. ѵ_кв = ѵ, 2ѵ, Зѵ.

Таким образом, для данного предельного случая квантовая и классическая теории приводят к одним и тем же результатам при расчете частот, излучаемых атомом водорода. Бор предполагает, что это приближенное равенство можно использовать и для определения интенсивности спектральных линий.

По классической теории, интенсивности главной частоты ѵ и обертонов 2ѵ, Зѵ, ... определяются коэффициентами разложения. По квантовой же теории, для определения интенсивностей соответствующих частот ѵ_кв = ѵ, 2ѵ, Зѵ, ... нужно знать вероятность переходов электрона с орбиты n на орбиты n— 1, n— 2, .... Бор и предполагает, что эти вероятности можно определять этими же коэффициентами. Таким образом, зная c^{1/sup>, c^{2/sup>, ..., можно сделать заключение и об интенсивности излучаемых частот. Это соответствие между классическим и квантовым рассмотрением для больших квантовых чисел справедливо и когда атом находится в магнитном или электрическом полях, а также и для более сложных атомов. Только в этих случаях в разложении Фурье для какой-либо из координат q электрона содержится уже не одна основная частота, а много частот и их гармоник. Тогда для больших квантовых чисел интенсивности излучаемых спектральных линий будут определяться соответствующими коэффициентами разложения.

Бор идет еще дальше. Он полагает, что аналогию между классическим и квантовым рассмотрением можно распространить и на небольшие квантовые числа, когда ѵкв нельзя даже приближенно считать равным какой-либо из ѵкл в разложении ряда Фурье. Но все же определенным ѵ_кв можно поставить в соответствие определенные частоты ѵ_кл в разложении Фурье. И в этом случае коэффициенты при определенной классической гармонике определяют соответствующие вероятности перехода, следовательно, и интенсивности соответствующих спектральных линий. Так, например, если какой-либо коэффициент в разложении Фурье равен нулю (данная частота отсутствует), то отсутствуют и соответствующий квантовый переход, а значит, и данная спектральная линия в рассматриваемом спектре. Существование такой аналогии или соответствия между квантовым и классическим рассмотрением Бор не объясняет. Этот принцип соответствия следует принять как факт, так же как и основные постулаты Бора. Принцип соответствия оказался очень полезным. Его использование дало возможность установить правила отбора для различных случаев.

Таким образом и были установлены правила отбора для квантовых чисел k и m. Оказалось, что квантовое число k, или введенное позднее азимутальное квантовое число l = k — 1, при квантовых переходах должны изменяться на ±1, а для квантового числа m существует правило: Δm = 0, ±1, поэтому не все спектральные линии, которые могли бы иметь место согласно вычислениям Зоммерфельда и Дебая, наблюдаются в действительности для нормального эффекта Зеемана. Получил обоснование и тот факт, что в том же явлении, а также в явлении Штарка определенные линии имеют определенную поляризацию и т. д.

Важным достижением квантовой теории Бора было также развитие им и другими исследователями представления о строении многоэлектронных атомов. При этом они опирались на периодический закон Менделеева и химические свойства элементов, а также использовали идею о слоистом строении атомов, заимствованную у Дж. Дж. Томсона. Впервые в развитом виде теорию строения атомов Бор изложил в 1921 г. в докладе «Строение атомов в связи с физическими и химическими свойствами элементов»¹⁴, прочитанном им в Копенгагене; затем она совершенствовалась в его последующих работах и работах других ученых. К этому времени уже было выяснено, что заряд ядра атома равен Ze, где Z — порядковый номер данного элемента в таблице Менделеева.

Таким образом, число электронов в атоме равно его порядковому номеру. Бор рассматривает атом как систему, образованную в результате последовательного присоединения электронов к ядру. Пусть имеется ядро с положительным зарядом, равным Ze. При захвате ядром одного электрона образуется система, подобная атому водорода, простейшим состоянием которого является состояние с энергией —2π²me⁴Z²/(h²n²) (n — главное квантовое число, равное единице).При этом и квантовое число k равно единице, т. е. мы получаем круговую орбиту. При Z = 1 имеем просто атом водорода в состоянии с наименьшей энергией. В результате прибавления к ядру второго электрона образуется система, подобная атому гелия, или просто гелий, если Z = 2. Исходя из ряда соображений о свойствах гелия, Бор полагает, что второй электрон в случае невозбужденного состояния имеет также круговую орбиту с теми же квантовыми числами пик, равными единице. Два электрона заполняют первую оболочку,названную K-оболочкой.Она представляет собой прочную систему, что выражается в химических свойствах гелия. Заполняя далее электронные оболочки, мы переходим к литию, атом которого имеет три электрона. На основании физических и химических свойств лития Бор заключает, что третий электрон должен находиться на орбите с n — 2 и k = 1, что говорит о том, что орбита третьего электрона является эллиптической. Конечно, такое представление об орбите третьего электрона приближенное, так как эта орбита проникает внутрь K-оболочки, в результате движение электрона более сложное. Однако для установления точной орбиты третьего электрона нужно было бы решать весьма трудную задачу движения многих тел.

Последующий захват электронов ядром приводит к последовательному заполнению новой оболочкой с n = 2, названной L-оболочкой. Орбиты этой оболочки различаются по виду и взаимной ориентации.

Десятый по счету электрон закончит заполнение К- и L-оболочек, и мы вновь получим устойчивую конфигурацию электронов, которая образует атом инертного газа неона. Подобным же образом образуется третья К-оболочка, которая содержит 8 электронов и также заканчивается инертным газом-аргоном. Затем следуют оболочки N и О, содержащие уже по 18 электронов, затем оболочка Р, имеющая 32 электрона, и, наконец, частично заполненная оболочка Q (рис. 32).

Естественно, что изложенные соображения Бора можно было рассматривать только лишь как начало теории строения сложных атомов. Развитие этой теории должно было заключаться в объяснении, почему электроны в атомах располагаются по оболочкам так, что в первой оболочке — два электрона, во второй — восемь и т. д. Такое расположение электронов в атоме не было объяснено Бором, а угадано на основании соображений полуэмпирического характера.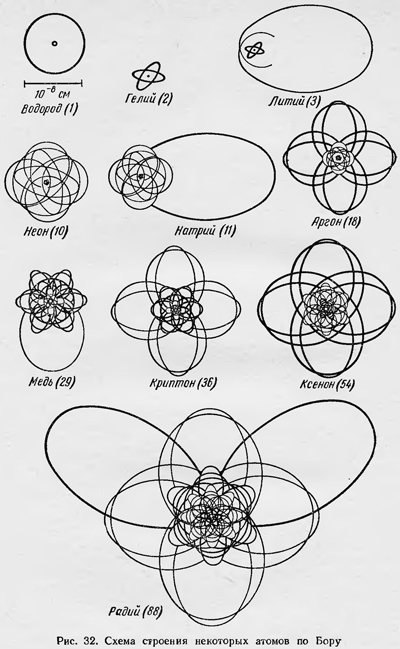

Дальнейшие исследования строения атома пошли по линии уточнения формы и взаимной ориентации электронных орбит и введения новых соответствующих квантовых чисел для состояний как отдельных электронов в атоме, так и состояния атома в целом. Еще в 1920 г. Зоммерфельд, изучая спектры щелочных металлов, их дублетный характер, ввел новое квантовое число j для характеристики состояния всего атома, которое назвал «внутренним квантовым числом». Это квантовое число определяло момент импульса всего атома, который является суммой моментов импульсов валентного электрона и заполненных оболочек, или «остова». После этого на основе ряда соображений вместо азимутального числа k было введено квантовое число l = k — 1, и выяснен странный факт, что электрон в состоянии с наименьшей энергией имеет момент импульса, равный нулю, а также что новое квантовое число j = l ± 1/2, откуда следует , что для случая отсутствия момента импульса l общий момент импульса всего атома не равен нулю, а равен ± 1/2 h/2π. В связи с этим он был приписан сначала «остову» атома, т. е. атому без валентного электрона. Далее оказалось, что для более сложных атомов, обладающих мультиплетным характером спектра, квантовое число j = 1 + s, где s — новое квантовое число, равное 0, ±1/2, ±1, ±3/2, ... .

В свою очередь, ряд физиков, в том числе и Бор, для систематики спектров многоэлектронных атомов вместо квантового числа k ввели два квантовых числа: k₁ и k₂. Одно из этих чисел должно было учитывать релятивистскую поправку, а другое — наличие экранировки орбит другими электронами. Вводились и другие системы квантовых чисел, характеризующие состояние или атома, или его отдельных электронов.

В 1925 г. немецкий физик Паули (1900—1958) сделал новый шаг в развитии как теории строения атома, так и квантовой теории вообще. Исследуя дублетный характер спектров щелочных металлов, а также аномальный эффект Зеемана, Паули высказал мысль, что их можно объяснить, если приписать самому электрону некоторую «двузначность», т. е. что электрон на орбите может находиться в двух состояниях. Он писал:

«Дублетная структура спектров щелочных металлов, а также нарушение теоремы Лармора согласно этой точке зрения объясняется своеобразной классически не описываемой двузначностью квантовотеоретических свойств излучающего электрона»¹⁵.

Что означает, однако, «двузначность» — этот вопрос Паули не был склонен рассматривать более подробно и предлагать для ее объяснения какую-либо модель. Но уже в том же 1925 г. американский физик Крониг, узнав об идеях Паули, высказал предположение, что эта «двузначность» является результатом того, что самому электрону нужно приписать момент импульса, равный 1/2 h/2π, и соответственный магнитный момент. Соображения Кронига не встретили поддержки ни у Паули, ни у ряда других ведущих теоретиков. Против гипотезы о вращении электрона можно было высказать много возражений, и она, казалось, не могла быть принята¹⁶.

Однако также в 1925 г. независимо от Кренига голландские физики Уленбек и Гаудсмит пришли к аналогичному заключению (и опубликовали его) о собственном моменте импульса электрона, который объяснялся вращением самого электрона вокруг своей оси¹⁷. Их работа вызвала интерес и хотя вскоре было выяснено, что представление о вращающемся электроне не может быть сохранено, тем не менее представление о спине электрона твердо вошло в физику.

Подтверждением гипотезы о собственном моменте импульса и магнитном моменте электрона свидетельствовали также опыты Штерна и Герлаха, проделанные ими еще в 1921 г. Штерн и Герлах пропускали узкий пучок атомов серебра через сильно неоднородное магнитное поле. При этом они обнаружили, что прошедший такое поле пучок атомов расщепляется на два. Результат этого опыта показывал, что атомы серебра обладают общим моментом импульса и магнитным моментом, который может принимать только две ориентации относительно направления магнитного поля. Атом серебра имеет один валентный электрон, который в невозбужденном состоянии характеризуется квантовым числом k = 1, и, как полагали сначала, моментом импульса электронной орбиты, который может принимать две ориентации. Поэтому первоначально ь результатах опыта Штерна и Герлаха видели подтверждение только пространственного квантования. Однако после того как выяснилось, что момент импульса электрона определяется квантовым числом l = k — 1 и что наименьшее значение этого числа l = О, указанная выше интерпретация результата опыта Штерна и Герлаха уже не годилась, так как момент импульса при движении валентного электрона по орбите равен нулю, соответственно и магнитный момент орбиты также должен быть равен нулю. С другой стороны, рассмотрение момента импульса атома серебра как момент импульса «остова» атома также встречало возражения. После того как была введена гипотеза спина электрона, опыт Штерна и Герлаха получил правильное толкование и стал рассматриваться как прямое подтверждение наличия спина у электрона.

Почти одновременно с гипотезой о «двузначности» электрона Паули высказал важное предположение, касающееся вопроса заполнения оболочек в атоме, известное как принцип Гіаули. Как выяснилось в конце концов, для характеристики состояния электрона в атоме необходимо четыре квантовых числа (одно из них появляется в результате существования спина) Согласно принципу Паули, в атоме не может быть двух или более электронов, для которых значения всех четырех квантовых чисел одинаковы. Он писал:

«Если в атоме есть электрон, для которого эти квантовые числа... имеют определенное значение, то это состояние «занято»¹⁸.

Принцип Паули проливал новый свет на теорию строения атома. Теперь стало понятным предположение Бора о последовательном заполнении электронных оболочек многоэлектроиных атомов. Действительно, для n = 1 возможны всего два различных состояния электрона в атоме на соответствующей орбите и оболочку К заполняют два электрона. Для n = 2 число различных состояний равно восьми и, действительно, вторую L-оболочку заполняет восемь электронов и т. д.

Вернер Гейзенберг

Введение четырех квантовых чисел, установление принципа Паули и объяснение периодической системы Менделеева — новые большие успехи теории атома Бора. Однако они по-прежнему не означали, что теорию можно считать удовлетворительной. Во-первых, сами постулаты Бора имели характер непонятных, ниоткуда не следуемых утверждений, которые должны были бы получить свое обоснование. Во-вторых, помимо основных постулатов теория содержала ряд других принципов: условия квантования, принцип соответствия, принцип Паули и т.д. Все они также нуждались в обосновании. Наконец, теория дала многое для выяснения строения атома и атомных спектров и т. д., однако ее применение часто встречало непреодолимые трудности уже в довольно простых случаях. Так, никакие попытки теоретически рассчитать даже такой, казалось бы, простой атом, как атом гелия, не привели к успеху. Неудовлетворительность теории атома ясно понималась самими физиками. Так, например, Паули в одном из своих писем в 1925 г. писал:

«Физика теперь снова зашла в тупик, во всяком случае для меня она слишком трудна, и я предпочел бы быть комиком в кино или кем-нибудь вроде этого и не слышать ничего о физике»¹⁹.

Такнм образом, перед физикой стояла задача нахождения новых путей развития теории атомных явлений. Эти пути потребовали отказа от целого ряда понятий и давно установленных принципов. Молодой немецкий ученый Гейзенберг установил основы так называемой матричной механики; французский физик де Бройль, а за ним австрийский физик Шредингер разработали волновую механику. Как вскоре оказалось, и матричная механика, и волновая механика — различные формы общей теории, получившей название квантовой механики.

¹Crookes W. Die Genesis der Elemente. Braunschweig, 1888.

²Морозов H. Периодические системы строения вещества. М., 1907, С, 399—400.

³Чичерин Б. Н. Система химических элементов.— ЖРФХО, вып. 3, 7, 1888; вып. 7, 8, 9, 1889. См, также: Чичерин Б. Н. Положительная философия и единство науки. М., 1892.

⁴Чичерин Б. Н. Положительная философия и единство науки, с. 120.

⁵Томсон Дж. Дж. Электричество и материя. М.—Л., Государств, изд-во. 1928

⁶Бор Н. Избранные научные труды. Т. I. М., «Наука», 1970, с. 325—326.

⁷Nagaoka H. Phil. Mag. (6), Vol. 7, 1904, p. 445.

⁸Wien W. Phys. Zs., В. 6, 1905, S. 806,

⁹Резерфорд Э. Избранные труды. М., «Наука», 1972, с. 238.

¹⁰Тhоmsоn J. J. Phil. Mag. (6). Vol. 26, 1913, p. 792.

¹¹Томсон Дж. Дж. Электрон в химии. М.—Л., 1927. Статическую модель атома для объяснения периодической системы элементов Менделеева применили также американские ученые: Льюис в 1916 г. (J. Amer. Chem. Soc. Vol. 38, 1916, p. 762) и Лэнгмюр в 1919 г. (J. Ашег. Chem. Soc. Vol. 41, 1919, p. 868).

¹²См. например: Фан-Левен Г. И. Гипотеза о строении атома. — ЖРФХО, т. 46, 1914, отд. 2, с. 153.

¹³Бор Н. Избранные научные труды. Т. I, с. 162—163.

¹³Бор Н. Избранные научные труды. Т. 1, с. 252.

¹⁴Бор Н. Избранные труды. Т. I, с. 318.

¹⁵Паули В. Труды по квантовой теории. М., «Наука», 1975, с. 644.

¹⁶Более подробно о введении понятия вращающегося электрона или о спине электрона см. в соответствующих статьях Р. Кренига и Б. Ван-дер-Вардена в кн.: Теоретическая физика XX века. М., ИЛ, 1962.

¹⁷Uhlenbeck G., Goudsmitt S. Naturwissenschaften Jahrg. 13, 1925, S. 953.

¹⁸Паули В. Труды по квантовой теории, с. 654.

¹⁹Теоретическая физика XX века М. ИЛ., 1962, с. 34.}}}}}}