§ 68. Развитие теории излучения и возникновение представлении о световых квантах
|
Работы Фраунгофера по изучению спектра Солнца, а затем и спектров земных источников света послужили началом развития спектроскопии. Спектроскопические исследования уже в 20-х годах прошлого столетия приводят к мысли о возможности спектрального анализа. Так, английский ученый Тальбот уже в 1826 г. высказывает идею спектрального анализа. Он говорил, что один «взгляд на спектр пламени показывает присутствие вещества, для определения которого в противном случае потребовался бы специальный химический анализ в лаборатории»1. Вместе с исследованием спектров излучения начинают обращать внимание и на спектры поглощения. При этом выясняется, что между излучением и поглощением тела существует простая связь. В спектрах поглощения отсутствуют или ослабляются те участки спектра которые испускаются данным телом. Важный шаг в развитии спектрального анализа был сделан Кирхгофом совместно с Бунзеном, которые разработали методику спектрального анализа.
Густав Кирхгоф (1824—1887) сформулировал новый закон, известный под именем закона Кирхгофа. В работе, опубликованной в 1860 г., и последующих работах он сформулировал и доказал этот закон, исходя из основных положений термодинамики. Он показал, что для лучей одной и той же длины волны при одной и той же температуре отношение испускательной и поглощательной способности для всех тел одно и то же. Или, другими словами, если ЕλТ и АλТ — соответственно испускательная и поглощательная способность тела, зависящие от длины волны λ и температуры Т, то 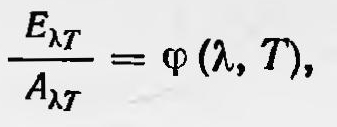
где φ(λ, Т) — некоторая универсальная функция λ и Т, одинаковая для всех тел. 
Густав Кирхгоф Кирхгоф ввел также понятие абсолютного черного тела как тела, поглощающего все падающие на него лучи, и дал известную его модель. Для такого тела, очевидно, АλТ=1 тогда универсальная функция Кирхгофа φ(λ, Т) равна испускательной способности абсолютно черного тела. Сам Кирхгоф не определил вид функции φ(λ, Т), а отметил только некоторые ее свойства. Встала задача определить вид этой функции. Функция φ(λ, Т) — универсальная, поэтому естественно было предполагать, что ее вид можно определить, исходя из теоретических соображений, а именно используя основные законы термодинамики. Однако задача определения вида функции Кирхгофа оказалась весьма трудной. Исследования в этом направлении, основанные на термодинамике и оптике, не привели к успеху. Удалось только выяснить особенности данной функции. Во-первых, удалось установить зависимость полного излучения абсолютно черного тела от температуры. Теоретически эта зависимость была найдена Больцманом в 1884 г. Но еще раньше эту формулу экспериментально установил Стефан. В связи с этим формула 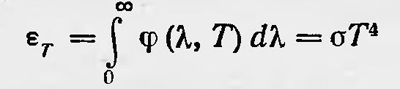
носит название закона Стефана—Больцмана. Здесь εТ — полная излучательная способность черного тела, σ — постоянная. В 1893 г. Вильгельм Вин (1864—1928) исследовал функцию Кирхгофа, опираясь на термодинамику и электродинамику или оптику. Он пришел к заключению, что она должна иметь вид 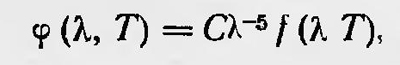
где f(λT) — новая функция λT. Отсюда следует, что λmT=const, т. е. что произведение температуры на длину волны, соответствующую максимальному значению излучаемой энергии, при этой температуре равна постоянной величине. Этот вывод известен в настоящее время как закон смещения Вина. Попытку определить вид функции Кирхгофа предпринял в 1887 г. Владимир Александрович Михельсон (1860—1927)2. Он понял, что для нахождения этой функции нельзя ограничиться рамками термодинамики и макроскопической электродинамики, а необходимо привлечь методы статистической физики, рассматривая излучающее тело как совокупность частиц, из которых каждая способна испускать и поглощать электромагнитную энергию. Рассматривая свою теорию как весьма приближенную, Михельсон использовал простую модель излучающего тела. Тело состоит из атомов, каждый из которых заключен в сферическую полость радиуса r, где движется со скоростью ѵ, испытывая упругие соударения со стенками полости. Хаотическое движение атома внутри полости можно представить в первом приближении как периодическое движение с периодом τ=4r/ѵ и принять, что атом излучает электромагнитную монохроматическую волну с таким же периодом. Чтобы определить интенсивность излучения в определенном интервале τ,τ+dτ, нужно знать число атомов nτ, период колебаний которых лежит в данном интервале и интенсивность излучения каждого такого атома іτ. Число атомов nτ Михельсон определяет с помощью закона распределения скоростей Максвелла, полагая, что скорости атомов ѵ распределяются поэтому закону. Учитывая, что ѵ=4r/τ и 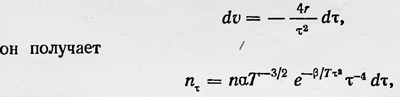
где n — общее число атомов в теле, Т — температура, α и β — постоянные. Для определения i Михельсон делает целый ряд предположений, используя которые находит, что 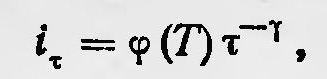
где γ — постоянная, φ(Т) — некоторая функция абсолютной температуры. Теперь удельную интенсивность излучения всего тела при температуре Т в интервале длин волн λ,λ + dλ, принимая во внимание, что τ= λ/с, можно записать в виде 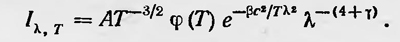
Далее, учитывая закон Стефана — Больцмана и введя некоторые дополнительные предположения, Михельсон окончательно получил 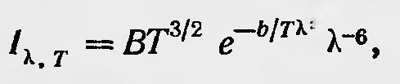
где B и b — новые постоянные. Он сравнивает этот результат с экспериментальными данными, полученными незадолго до этого, по измерению распределения энергии в спектре черного тела. Сравнение показывает, что теоретическая кривая, построенная по формуле Михельсона качественно соответствует экспериментальным кривым. В частности, из формулы Михельсона следует, что λ2mT=const, где λm — длина волны участка спектра, имеющая наибольшую интенсивность. Отсюда следует, что при увеличении температуры максимум кривой должен смещаться в коротковолновую часть спектра. Экспериментальные данные подтверждают этот вывод. Однако вскоре более точные измерения показали, что закон, полученный Михельсоном, неправильный. Кроме того, как отмечалось выше, Вин получил новый закон — закон смещения Вина, согласно которому не λ2mT= const, а λmT=const. В 1896 г. Вин вывел новую формулу для закона распределения энергии в спектре черного тела3. Он рассматривал совокупность молекул, помещенных внутри полости, испускающих и поглощающих излучение. В случае термодинамического равновесия скорость молекул должна быть распределена по закону распределения Максвелла. Далее, как и Михельсон, Вин предположил, что длины волн, испускаемых и поглощаемых молекулой, определяются ее скоростью. Однако Вин предложил другую зависимость λ от ѵ, нежели Михельсон. Если последний предположил, что ѵ ~ ѵ или ѵ ~ 1/λ, то Вин, исходя из закона смещения, который был им уже установлен, положил, что V2 ~ v или V2 ~ 1/λ. Затем Вин, подобно Михельсону, применил закон распределения скоростей Максвелла и получил, что число атомов, излучающих и поглощающих излучение в промежутке длин волн λ,λ + dλ, таково: 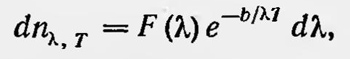
где F(λ) — пока неизвестная функция. Используя затем закон Стефана — Больцмана и проводя некоторые преобразования, он окончательно получил закон, известный как закон распределения Вина: 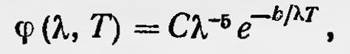
где С и b — постоянные. Формула, полученная Вином, оказалась приближенной. Экспериментальные исследования показали, что она непригодна при переходе в длинноволновую часть спектра, точнее, когда XT становится большим. Таким образом, перед физиками по-прежнему стояла задача нахождения закона распределения энергии в спектре излучения черного тела, пригодного и для коротких и для длинных волн. В 1900 г. в результате работ целого ряда физиков были предложены новые формулы. Прежде всего нужно отметить работу Релея4, который подошел к данной задаче с новых позиций. Он исходил из закона равномерного распределения энергии по степеням свободы. Релей представил излучение в замкнутом объеме как совокупность стоячих монохроматических волн и предположил, что каждой такой волне нужно приписать две степени свободы. Тогда для случая термодинамического равновесия на каждую монохроматическую волну должна приходиться в среднем энергия, равная kT. Руководствуясь этим положением, Релей получил новую формулу для распределения энергии в спектре черного тела: 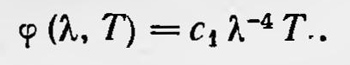
Впоследствии эту формулу, исходя из тех же представлений, более строго обосновал Джинс. Однако она оказалась справедливой только для длинных волн. Из нее следовало, что общая энергия, излучаемая телом при данной температуре, равна бесконечности, что абсурдно. 
Макс Планк Действительно, 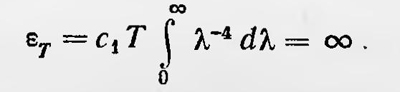
Несмотря на это, Джинс пытался отстаивать правильность основных положений, на основе которых была получена эта формула, и правильность конечного вывода. Он высказал предположение, что для установления термодинамического равновесия между излучением и веществом требуется бесконечно большое время, в результате термодинамическое равновесие никогда не устанавливается. Таким образом, наблюдаемое распределение энергии в спектре черного тела не является, строго говоря, равновесным в термодинамическом смысле. В 1900 г. в октябре на заседании Берлинского физического общества Макс Планк (1858—1947) предложил новую формулу для распределения энергии в спектре черного тела, полученную первоначально полуэмпирическим путем. Еще раньше, занимаясь вопросами теории излучения, Планк нашел ряд соотношений. При этом он использовал простую модель, рассматривая пространство, ограниченное зеркальными стенками и заполненное излучением, в котором находилась совокупность независимых гармонических осцилляторов, обладающих всевозможными собственными частотами. В этом пространстве в результате непрерывного поглощения и испускания излучения осцилляторами должно устанавливаться термодинамическое равновесие между осцилляторами и излучением. При этом излучение должно стать черным, т. е. распределение энергии по частотам должно быть таким, как и в спектре черного излучения. Пользуясь такой моделью, Планк нашел, что плотность ρv,T энергии излучения для интервала частот ѵ,ѵ+dv должна быть равна 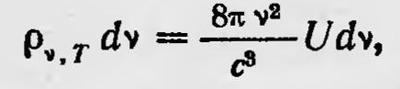
где U — средняя энергия осциллятора, имеющего собственную частоту v,. Полагая, что ρv,T выражается через закон Вина, и используя второй закон термодинамики, Планк определил, что между энтропией S, отнесенной к одному осциллятору, и его средней энергией существует простое соотношение 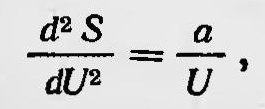
где а — постоянная. В простоте полученного соотношения Планк видел сначала подтверждение справедливости формулы Вина. В своей автобиографии он писал: «Эта связь была столь поразительно простой, что некоторое время я считал ее совершенно общей ...»5. Но, как уже говорилось выше, измерения показали, что формула Вина перестает быть справедливой для больших значений λТ. Следовательно, для этого случая неверно и соотношение, полученное Планком. Однако, как заметил Планк для этого случая, если исходить из известных экспериментальных данных, можно предположить также простое соотношение 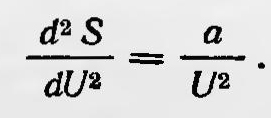
Это обстоятельство натолкнуло Планка на мысль, что истинное выражение для 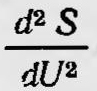 должно быть таким, чтобы для случая малых λТ оно было бы обратно пропорционально U, а для больших значений — U2. Наиболее простое выражение для должно быть таким, чтобы для случая малых λТ оно было бы обратно пропорционально U, а для больших значений — U2. Наиболее простое выражение для 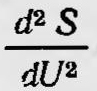 , удовлетворяющее этому условию, таково: , удовлетворяющее этому условию, таково:
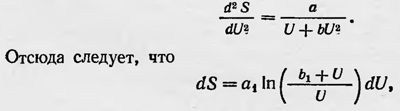
где а1 и b1 — новые постоянные. Принимая теперь во внимание, что при постоянном объеме dS=dU/T, и используя закон смещения Вина, Планк получил 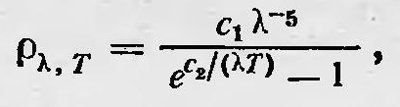
где с1 и с2 — постоянные. Формулу, предложенную Планком, сравнили с экспериментальными данными, которые прекрасно ее подтвердили. Таким образом, никаких сомнений в ее справедливости не могло возникнуть. Через несколько недель Планк дал этой формуле более строгое теоретическое обоснование, сообщив о результатах своей работы на заседании Берлинского физического общества6. В первой работе условием успеха Планка послужило то, что он сумел удачно подобрать соотношение между энтропией, отнесенной к одному осциллятору, и его средней энергией. В новой работе он старается решить эту задачу, исходя уже из теоретических соображений, обращаясь к статистическим представлениям Больцмана о связи между энтропией и вероятностью. Вероятность какого-либо макроскопического состояния идеального газа Больцман определял числом микросостояний, реализующих это макросостояние. Планк применяет этот метод для осцилляторов и полагает, что вероятность W определенного распределения энергии Е между N осцилляторами, обладающими собственной частотой ѵ, равна числу способов, с помощью которых эта энергия может распределяться между ними. Однако такая постановка вопроса имеет смысл только в том случае, если энергия Е распределяется между осцилляторами конечными порциями, кратными некоторой величине ε. В связи с этим Планк полагает, что Е = Рε, где Р — целое число. Если принять эту гипотезу, то вероятность W, равная числу способов, с помощью которых энергия Е может быть распределена между N осцилляторами, согласно правилам комбинаторики равна 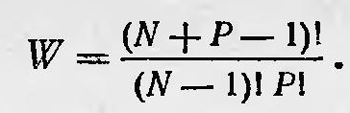
Применяя формулу Стирлинга, полагая, что Р — большое число в первом приближении, имеем 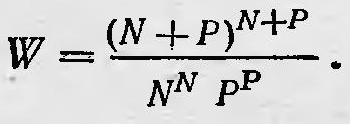
Но так как между вероятностью и энтропией, согласно основному положению статистической физики, существует соотношение S=kInW, то Планк получает для энтропии N осцилляторов выражение SN=k[(N + Р) ln (N + Р) —NInN — PInP]. 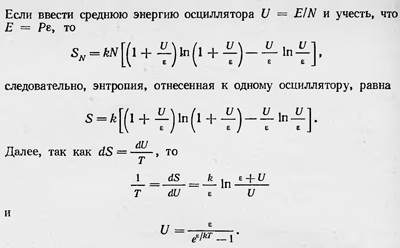
Применяя, наконец, закон смещения Вина и выражение, связывающее U и ρv,T, получим, во-первых, что ε=hѵ, где h — некоторая постоянная, и, во-вторых , 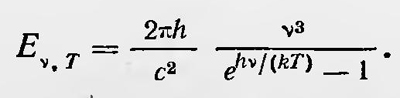
т. е. тот самый закон, который Планк ранее получил для распределения энергии в спектре черного излучения полуэмпирическим путем. Отсюда для излучательной способности черного тела справедлива формула 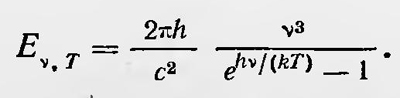
В формулы Планка входят постоянные k и h, которые он мог определить на основе экспериментальных данных, полученных при измерениях распределения энергии в спектре черного излучения. Планк находит, что k = 1,346•10-6 эрг•град и h = 6,55•10-27 эрг•с. (Постоянная k является постоянной Больцмана и равна R/N, где R — универсальная газовая постоянная, а N — число Авогадро. Зная k и R, можно определить число Авогадро. По данным Планка, N = = 6,175•1023, что, как известно, находится в согласии со значениями этого числа, вычисленными из совершенно других соображений. Смысл постоянной h был неясен. Первоначально разделение энергии на части, кратные ε, казалось просто математическим приемом, с помощью которого подсчитывалась термодинамическая вероятность различных распределений энергии по осцилляторам. Однако величина ε вошла в окончательный результат, причем так, что от нее нельзя было освободиться, устремляя ее к нулю, так как тогда получалась бы неверная формула. Больше того, ε не является любой величиной, а именно ε = hѵ, где h — совершенно определенная константа. Все это было неясным, так как вело к признанию наравне с атомизмом вещества атомизма энергии или действия, что не укладывалось в рамки основных представлений классической физики. Поэтому казалось естественным, что многие другие физики рассматривали введение конечных порций энергии только как рабочую гипотезу, как математический прием, полагая, что со временем формула Планка получит «нормальное» обоснование на основе общих представлений. Так расценивал теорию Планка, например, Лоренц, который писал: «В этой теории несомненно, заключается значительная доля истины. Конечно, она ни в коей мере не послужила для того, чтобы раскрыть механизм явлений; следует также признать, что весьма трудно найти оправдание для такого представления о распределении энергии порциями конечной величины, которые даже не равны друг другу...»7. Одновременно ряд ученых, в том числе и сам Планк, надеялись обосновать основную гипотезу о распределении энергии конечными порциями на основе представлений классической физики. Некоторые из них считали возможным использовать для этой цели модель атома Дж. Дж. Томсона, согласно которой атом состоит из сферы, равномерно заполненной положительным зарядом, внутри которой находятся отрицательно заряженные электроны. Электроны под действием падающего излучения приходят в движение. Но пока они находятся внутри сферы, их движение является упорядоченным и не связано с истинным поглощением лучистой энергии, а приводит лишь к рассеянию света и дисперсии. Иначе дело обстоит, если под влиянием падающего на атом излучения электрон покинет положительную сферу и начнет участвовать в хаотическом тепловом движении. В этом случае произойдет поглощение лучистой энергии, которая перейдет в тепловую энергию тела; для такого процесса требуется определенная конечная энергия, поэтому атом будет поглощать энергию конечными порциями. Обратный процесс, когда электрон, участвуя в тепловом движении, теряет энергию и захватывается атомом, соответствует излучению лучистой энергии. При этом излученная энергия опять-таки имеет определенное конечное значение и процесс излучения, как и процесс поглощения, происходит конечными порциями — квантами энергии. Предлагались и другие модели для обоснования основной гипотезы Планка. Однако все они, как и предыдущая, имели искусственный характер, и хотя с их помощью удавалось получить иногда даже правильные количественные соотношения, они не могли считаться удовлетворительными. Новые идеи по поводу квантовой гипотезы Планка были высказаны Н. А. Умовым в 1913 г.8. Рассматривая термодинамическое равновесие между излучением и веществом, он полагал, что излучение, или эфир, обладает ограниченной степенью чувствительности по отношению к хаотическому движению молекул вещества. Это означает, что только часть энергии молекул вещества, находящихся в тепловом движении, эфир воспринимает индивидуальными толчками от каждой молекулы. Остальная же часть энергии воспринимается эфиром как средняя энергия, подобно макроскопическому телу, и определяется средними величинами, в частности температурой. Если предположить, что чувствительность эфира выражается величиной 1/ε,где ε = hv, то из гипотезы Умова следовало, что при термодинамическом равновесии действует закон Планка. Сам Планк в течение довольно длительного времени пытался дать классическое обоснование закону черного излучения или, во всяком случае, приблизить его вывод к классическим представлениям. В 1911 г. он опубликовал работу9, в которой предполагал, что только процессы испускания электромагнитного излучения имеют прерывный квантовый характер, тогда как процессы поглощения происходят непрерывно. Такая гипотеза, по Планку, также приводит к закону излучения, аналогичному полученному в 1900 г. Только в этом случае средняя энергия осциллятора 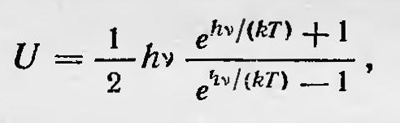
т. е. из новой теории следует, что осцилляторы обладают средней энергией и при температуре абсолютного нуля. Таким образом, впервые была высказана идея о существовании нулевой энергии, которая позже приобрела определенный смысл. В 1914 г. Планк выдвинул новую теорию10, согласно которой испускание и поглощение электромагнитного излучения осцилляторами происходят непрерывно. Зато при процессах столкновения осцилляторов с частицами, молекулами, ионами, электронами энергия осцилляторов изменяется скачком на величину, кратную hѵ. Эта теория была предложена Планком в связи с теорией Бора о дискретных состояниях атомов (Планк ссылался на известные опыты Франка и Герца). Используя данные представления, Планк получил правильный закон распределения энергии в спектре черного излучения. Однако вскоре выяснилось, что некоторые результаты этой теории не могут быть согласованы с рядом экспериментальных данных. Таким образом, все попытки каким бы то ни было образом дать классическое или «полуклассическое» обоснование основной гипотезе Планка или приблизиться к нему не приводили к положительным результатам. Становилось все более и более ясно, что эта гипотеза по своей сущности чужда классическим представлениям. Вспоминая о попытках дать классическое обоснование своей основной гипотеез, Планк писал: «Крушение всех попыток перебросить мост через возиищную пропасть вскоре уничтожило все сомнения: Или квант действия был фиктивной величиной — тогда весь вывод закона излучения был принципиально иллюзорным и представляет просто лишенную содержания игру в формулы, или при выводе этого закона в основу была положена правильная мысль — тогда квант действия должен был играть в физике фундаментальную роль, тогда появление его возвещало нечто дотоле неслыханное, что, казалось, требовало преобразования самих основ нашего физического мышления, покоившегося со времени обоснования бесконечно малых Ньютоном и Лейбницем на предположении о непрерывности всех причинных связей»11. В 1911 г. происходил первый Сольвеевский конгресс физиков. Руководил его работой Лоренц. В дискуссии участвовали Ланжевен, Пуанкаре, Планк, Нернст, Резерфорд, Эйнштейн, Вин, М. Кюри и некоторые другие. Конгресс был посвящен «теории излучения и квантам» — злободневной проблеме физиков в то время. И понималась она участниками конгресса в основном как проблема дать классическое толкование теории излучения Планка, а также новым вопросам, связанным с теорией кванта. Никаких разумных идей в этом направлении на конгрессе высказано не было. Сложившуюся в физике ситуацию очень четко и определенно выразил Пуанкаре. Он прямо заявил, что гипотеза Планка не может быть согласована с представлениями классической физики. Она является для нее совершенно чуждой. «Новые, обсужденные здесь исследования, кажется, ставят под вопрос не только основные принципы механики, но даже те основные понятия, которые до сих пор были связаны с представлением о естественнонаучном законе вообще»12. Конечно, если бы гипотеза Планка нужна была только для объяснения закона черного излучения, то возможно, что она не вызвала бы столь острой постановки вопроса. Дело обстояло сложнее. Эту гипотезу вскоре с большим успехом начали применять для объяснения других явлений, которые нельзя было объяснить на основе представлений классической физики. Одной из трудностей, с которыми столкнулась классическая физика, было объяснение теплоемкостей с точки зрения кинетической теории тепла. Классическая кинетическая теория приводила к выводу, что при статистическом равновесии на одну степень свободы должна приходиться в среднем энергия, равная — kT. Вычисленные на основе этого вывода теплоемкости тел часто оказывались правильными, но были известны и случаи, когда экспериментальные результаты противоречили теоретическим выводам. Это относилось, в частности, к теплоемкости твердых тел. В соответствии с классической теорией для всех этих тел молярная теплоемкость должна быть равна 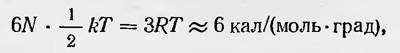
что соответствовало установленному еще в начале XIX в. закону Дюлонга и Пти. Однако было известно, что закон Дюлонга и Пти выполняется не всегда. Если для многих твердых тел при обычных температурах этот ѳакон справедлив, то при низких температурах он не действителен, так как с понижением температуры теплоемкость твердых тел уменьшается. Для некоторых же веществ этот закон не выполняется уже при обычных температурах. Несогласие теории и эксперимента не могло быть объяснено классической физикой. Эйнштейн в 1907 г. предложил13 объяснить зависимость теплоемкости от температуры, используя гипотезу квантов. Он предположил, что энергия осциллятора может изменяться только на конечную величину не только при взаимодействии его с излучением, но и в результате взаимодействия его с другим осциллятором или при соударении его с частицей и т. д. Тогда если представить себе твердое тело состоящим из правильно расположенных в узлах кристаллической решетки частиц-осцилляторов частоты ѵ, которые под влиянием взаимодействия друг с другом приходят в тепловое движение, то нужно учитывать, что их энергия может изменяться только на величину, кратную Лѵ. Такое предположение приводит к выражению для средней энергии, приходящейся на одну степень свободы, которое отлично от выражения, даваемого классической теорией. Эйнштейн получил, что средняя энергия, приходящаяся на одну степень свободы, в этом случае равна 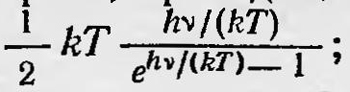 или на один грамм-моль: или на один грамм-моль: 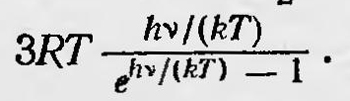
Отсюда теплоемкость твердого тела при постоянном объеме 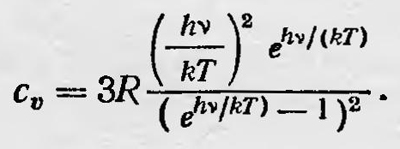
Формула, полученная Эйнштейном, в общем соответствовала экспериментальным данным. Для высоких температур она приводит к закону Дюлонга и Пти, при низких же температурах теплоемкости уменьшается и при Т→0 также стремится к нулю, что соответствует эксперименту. Однако полученную формулу для теплоемкости твердых тел нельзя было считать достаточно точной. При ее выводе предполагалось, что все частицы в узлах решетки представляют собой гармонические осцилляторы, обладающие одной и той же собственной частотой. В действительности же тепловые колебания молекул более сложные и их нельзя представить как гармонические с одинаковой частотой. Нернст и Линдеман несколько усложнили формулу для теплоемкости твердых тел, предположив, что частицы тела совершают колебания с частотами ѵ и ѵ/2. Однако и это предположение нельзя было считать вполне удовлетворительным. Следовало, как в последующем подчеркнул сам Эйнштейн, учесть всевозможные частоты колебаний частиц твердого тела. Однако для вычисления теплоемкости нужж> было бы знать набор частот ѵn, т. е. решить весьма трудную и сложную задачу. В 1912 г. Дебай14 предложил приближенный метод решения задачи нахождения теплоемкости твердого тела. Он рассматривал твердое тело как упругую сплошную среду. Исходя из этого, Дебай нашел выражение числа собственных колебаний Z в теле, имеющих частоту меньше некоторой заданной частоты ѵ: 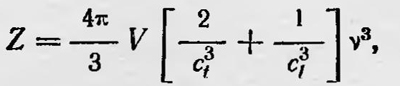
тде V — объем тела, ct и сl, — соответственно скорости распространения поперечных и продольных колебаний в теле. Отсюда число колебаний, соответствующих частотам от v до v + dv, равно 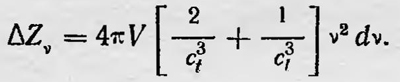
Но в сплошной упругой среде число всевозможных частот колебаний равно бесконечности, тогда как в действительности в твердом теле это число равно 3N, где N — число частиц, образующих тело. Поэтому Дебай предложил ограничить спектр частот и считать, что не существует колебаний с частотой, превосходящей максимальную частоту ѵтах, значение которой определяется из условия 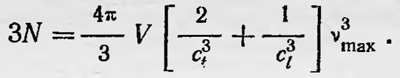
Следовательно, общее число колебаний, соответствующих интервалу частот ѵ,ѵ +dv, можно записать в виде 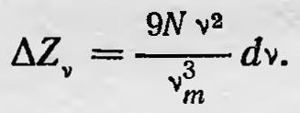
Применяя выражение Планка для среднего значения энергии осциллятора, получаем значение общей энергии: 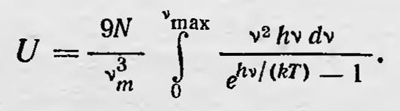
Отсюда, дифференцируя U по T, находим выражение для теплоемкости твердого тела. В принятых обозначениях для молярной теплоемкости при постоянном объеме имеем 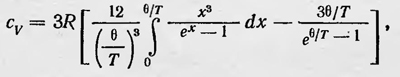
где 0 — так называемая характеристическая температура, введенная Дебаем: Ѳ = hvm/k. Для высоких температур сv = 3R, что находится в согласии с законом Дюлонга и Пти. В случае низких температур 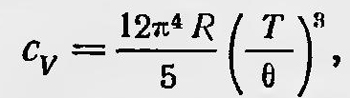
что также хорошо соответствует экспериментальным данным, полученным при исследовании зависимости теплоемкости от температуры. Теория теплоемкости твердого тела была далее разработана Борном и Карманом в том же 1912 г. В отличие от Дебая они рассматривали твердое тело как кристаллическую решетку, в узлах которой находятся частицы тела15. Существенно новым в развитии квантовой теории было введение понятия квантов света. Еще в 1903 г. Дж. Дж. Томсон высказал мысль об игольчатом строении светового излучения. Рассматривая прохождение рентгеновских лучей через газы и определяя их ионизирующую способность, он отметил, что обнаруженные при этом закономерности можно объяснить, если предположить, что рентгеновские лучи обладают, говоря современным языком, корпускулярными свойствами. Томсон писал, что трудности в объяснении явления прохождения рентгеновских лучей через газ отпадают: «Если вместо того, чтобы рассматривать фронт рентгеновской волны однообразным, мы предположим, что он состоит из очень ярких пятен, разделенных промежутками, где яркость очень мала, потому что в этом случае не только все молекулы, а вероятно даже разные части одной и той же молекулы, подвергаются различным условиям; этот случай аналогичен пучку катодных лучей, проходящих через газ; при этом число молекул, приходящих в столкновение с лучами, может быть очень малой частью всего числа молекул»16. Эта идея в более развитой форме уже под влиянием ги потезы Планка была разработана в 1905 г. Эйнштейном и применена им для объяснения оптических явлений и, в частности, фотоэффекта. К началу XX в. была открыта странная на первый взгляд закономерность, заключающаяся в том, что скорость фотоэлектронов не зависит от интенсивности света, а определяется только его частотой и что для каждого вещества существует определенная предельная частота, ниже которой фотоэффект не наблюдается. Эту закономерность нельзя было объяснить с точки зрения классической электродинамики, гипотеза же квантов, как показал Эйнштейн, объясняет ее очень просто. Эйнштейн предположил, что не только поглощение и испускание электромагнитного излучения происходят конечными порциями энергии, но что само излучение существует в виде отдельных дискретных объектов — квантов света. Он подчеркнул, что электромагнитная теория света встречается с трудностями при объяснении процессов, в которых происходит поглощение или испускание электромагнитного излучения. Эти явления можно объяснить, если принять, что световая энергия распределяется в пространстве не непрерывно. «Согласно этому сделанному здесь предположению,— писал Эйнштейн,— энергия пучка света, вышедшего из некоторой точки, не распределяеіся непрерывно во все возрастающем объеме пространства, а складывается из конечного числа локализованных в пространстве неделимых квантов энергии, поглощаемых или возникающих только целиком»17. Такую гипотезу Эйнштейн и принял, полагая величину квантов равной hv. Эйнштейн исходит из закона Вина, который справедлив для больших значений ѵ/Т в случае, когда плотность энергии излучения невелика, и подчеркивает, что его теория еправедлива только для этого случая. Принимая во внимание закон Вина 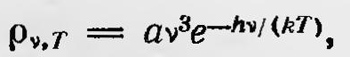 справедливый для этого случая, Эйнштейн находит выражение для энтропии монохроматического излучения S, помещенного в сосуд с идеально отражающими стенками, когда это излучение занимает только часть V всего объема сосуда Ѵ0: справедливый для этого случая, Эйнштейн находит выражение для энтропии монохроматического излучения S, помещенного в сосуд с идеально отражающими стенками, когда это излучение занимает только часть V всего объема сосуда Ѵ0:
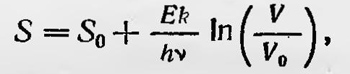
где Е — энергия излучения, S0 — энтропия, еели излучение распределено равномерно по всему объему Ѵ0. Далее, учитывая соотношение S = kInW, получаем, что относительная вероятность того, что все излучение содержится только в части V всего объема сосуда, равна 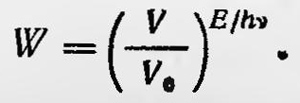
Но если теперь рассмотреть тот же сосуд, заполненный молекулами идеального газа, то вероятность того, что все эти n молекул находягея в объеме V, такова: 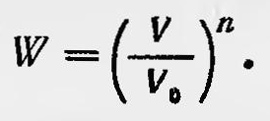
Таким образом, излучение частоты ѵ ведет себя аналогично идеальному газу с числом частиц, равным E/hv, и его можно рассматривать состоящим из дискретных образований квантов, величина которых hv. Принятая гипотеза позволила Эйнштейну легко объяснить ряд оптических явлений, относящихся к взаимодействию света и вещества, и, в частности, явление фотоэффекта. Эйнштейн получает известное уравнение, выражающее закон фотоэффекта: 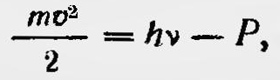
где mv2/2 — энергия фотоэлектрона; Р — энергия, затрачиваемая электроном при выходе из катода. Справедливость этого уравнения была проверена экспериментально. Получено хорошее совпадение теории с результатами опыта. Первоначально гипотезе световых квантов никто не был склонен придавать серьезного значения, сам Эйнштейн называл ее лишь эвристической гипотезой. Она никак не вязалась с представлениями о природе световых явлений, в основе которых лежала электромагнитная теория поля. Более того, гипотеза казалась возвращением к давно забытой корпускулярной теории света. Некоторые физики считали, что такая гипотеза является лишней даже и для объяснения фотоэффекта, полагая, что можно ограничиться гипотезой Планка о дискретности энергии, излучаемой и испускаемой осцилляторами, из которых состоит вещество. Само же излучение должно иметь непрерывный характер и подчиняться уравнениям Максвелла. Этого мнения придерживался и Планк, который неодобрительно отозвался о гипотезе световых квантов, считая ее излишней. Но постепенно у некоторых ученых зреет идея о том, что свет действительно обладает наряду с волновыми еще и корпускулярными свойствами и что на очередь встает задача объяснить этот дуализм и рассмотреть структуру распространяющихся световых возмущений. При этом пока еще предполагалось, что эта задача может быть решена с позиции обычных классических представлений. В 1909 г.18 Эйнштейн, продолжая исследования по теории излучения, признает, что свет обладает одновременно и волновыми и корпускулярными свойствами. В первой работе, в которой Эйнштейн высказал и применил впервые гипотезу о свойствах квантов, он исходил из закона Вина. Теперь он исследует вопрос о том, к каким результатам приведет теория, если исходить из закона Планка. Эйнштейн показывает, что если в полости, заполненной черным излучением, поместить идеально отражающую пластинку, то она должна испытывать флуктуации давления, подобно пластинке, помещенной внутри газа. Исходя из закона Планка, он рассчитывает величину среднего квадрата флуктуации давления на пластинку, приводя конечный результат. Если его видоизменить и записать выражение для флуктуации среднего значения квадрата энергии излучения в единице объема еа для интервала частот ѵ, ѵ + dv, то получаем 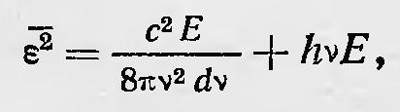
где Е — средняя энергия излучения, приходящаяся на единицу объема. Полученный результат можно интерпретировать следующим образом. Первый член в формуле для ε2 представляет собой выражение для флуктуации излучения, если исходить из волновой теории света. В этом случае флуктуации объясняются беспорядочным отражением волн от стенок полости, в которой заключено излучение, и от их интерференции. Второй член описывает флуктуации, подобные тем, которые имеют место в системе частиц при их хаотическом движении. При этом первый член полученного выражения играет основную роль в случае малых частот, когда справедлива формула Рэлея — Джинса и излучение проявляет волновые свойства. Наоборот, второй член играет основную роль в случае больших частот, для которых справедлива формула Вина, при этом излучение проявляет корпускулярные свойства. В общем же случае излучение обладает и корпускулярными и волновыми свойствами. Эйнштейн высказывает мысль, что этому можно в будущем дать объяснение, развивая теорию электромагнитного излучения или поля. Он пишет: «Все же мне кажется пока наиболее естественным, что появление вэлекгромагнитных полей света должно быть связано с особыми точками так же, как появление электростатических полей — с электронной теорией. Не исключено, что в такой теории всю энергию электромагнитного поля можно будет считать локализованной в этих особых точках, совсем как в старой теории дальнодействия. Я представляю себе каждую такую точку окруженной силовым полем, которое в основном имеет характер плоской волны ε амплитудой, уменьшающейся с удалением от особой точки. Если большое число таких особых точек находится на расстоянии, малом по сравнению с размерами силового поля одной особой точки, то силовые поля будут перекрываться и в целом дадут волновое силовое поле, быть может, очень мало отличающееся от волнового поля в смысле современной электромагнитной теории света. Вряд ли стоит подчеркивать, что до тех пор, пока такая картина не приведет к точной теории, ей не следует придавать особого значения. Я хотел только показать е ее помощью, что нельзя считать несовместимыми обе структуры (волновая и квантовая), которыми одновременно должно обладать излучение в соответствии с формулой Планка»19. Идея о том, как можно совместить корпускулярные и волновые свойства света, высказывалась другими физиками даже в более конкретной и развернутой форме. Например, обсуждалось предположение о том, что световое возмущение является совокупностью отдельных монохроматических волновых образований — квантов света, занимающих определенный объем в пространстве и распространяющихся как нечто целое. Однако все подобные интерпретации корпускулярно-волнового дуализма электромагнитного излучения встречались с большими трудностями при объяснении явлений интерференции и дифракции и даже простых явлений отражения и преломления света. Как можно объяснить, например, явление интерференции с точки зрения такой теории? Ведь интерферируют всегда только когерентные лучи света. Поэтому либо нужно было признать, что при образовании когерентных пучков света, например при отражении, разделяется один и тот же квант света или же что когерентны различные кванты света. Первое предположение противоречило известным уже в начале XX в. фактам наблюдения интерференции при большой разности хода (для видимой части спектра эта разность хода была порядка метра). Таким образом, нужно было признать существование фотонов соответствующих размеров, что представлялось совершенно неразумным. Как могли бы такие фотоны проникать, например, на сетчатку глаза через зрачок? Но и другая точка зрения, согласно которой кванты света в световом пучке образуют когерентный ансамбль, также встречала затруднения. Сейчас же возникает вопрос — почему при частичном отражении световых лучей на границе двух сред одни фотоны отражаются, а другие — преломляются? Каким образом фотоны, прошедшие на то место экрана, где наблюдаются темные полосы, уничтожают друг друга и т. д.? Возникали те же самые вопросы, перед которыми пасовала корпускулярная теория света Ньютона. Таким образом, перед квантовой теорией света, казалось, возникали непреодолимые трудности, поэтому многие физики отвергали представление о квантах света и рассматривали гипотезу Эйнштейна в лучшем случае как чисто эвристическую гипотезу, которая не отражает действительного существа светового излучения. В лекциях, прочитанных в Геттингене в 1910 г., Лоренц, проанализировав попытки объяснить гипотезу квантов света и показав их несостоятельность, определенно высказался против этой гипотезы. «Докладчик,— сказал он,— не хотел бы оспаривать эвристическую ценность этих гипотез; он лишь защищает старую теорию до тех пор, пока это возможно»20. Подобного рода взгляд на гипотезу Эйнштейна высказал и Милликен. В своей книге «Электрон», вышедшей в 1917 г., он писал: «... физическая теория, символическим выражением коей это уравнение должно было быть, оказалась столь неудачной, что сам Эйнштейн, как мне кажется, больше ее не поддерживает; мы находимся в таком положении, как если бы мы выстроили великолепное здание, а затем выбили все подпорки, не свалив самой постройки. Здание стоит целое, и, по-видимому, хорошо проверенное, но никаких подпорок не видно. Эти подпорки, очевидно, должны существовать, и самая увлекательная задача физики — найти их» 21. В 20-х годах были получены новые экспериментальные подтверждения теории световых квантов. Американский физик А. Комптон в 1922 г. обнаружил, что при рассеянии легкими элементами жестких рентгеновских лучей в рассеянном излучении появляются лучи с измененной длиной волны, причем длина волны этих лучей зависит от угла рассеяния. Классическая теория рассеяния электромагнитного излучения не объясняла это явление. С точки же зрения квантовой теории это явление, получившее название эффекта Комптона, легко объяснялось. Комптон, а также независимо от него Дебай дали теорию этого явления. Они рассматривали его как результат соударения фотонов с электронами атомов, на которых происходят рассеяние рентгеновских лучей. Элементарная теория эффекта Комптона, как известно, основывается на применении к процессу соударения фотона с электроном закона сохранения энергии и закона сохранения импульса. Полагая, что электрон до удара покоится, имеем два уравнения: 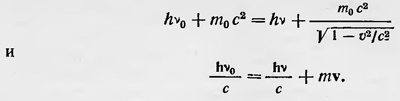
Здесь, как обычно, ѵ0 — частота падающих рентгеновских лучей; ѵ — частота рассеянных лучей; m0c2 — энергия покоящегося электрона; hѵ0 и hѵ — энергия и hѵ0/с и hѵ/с — соответственно импульс падающего и рассеянного фотонов. Из этих уравнений можно определить ѵ0— ѵ или λ— λ0 = Δλ. и получить, что 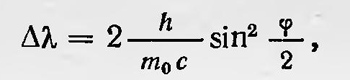
где φ — угол между направлением первоначального и рассеянного рентгеновского излучения. Выражение для Δλ хорошо соответствовало данным эксперимента, проведенного Комптоном. 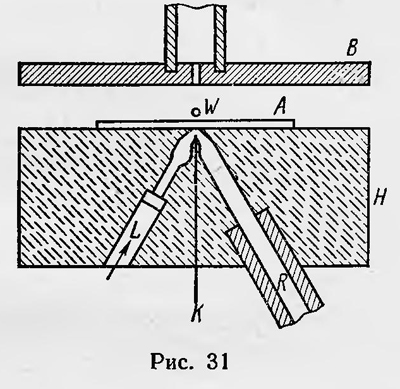
Существовали и другие экспериментальные подтверждения гипотезы квантов света. Это, например, опыт, проделанный в 20-х годах А. Ф. Иоффе и Н. И. Добронравовым22. Они наблюдали поведение маленькой висмутовой пылинки, помещенной внутри конденсатора и облучаемой рентгеновскими импульсами, которые исходили из почти точечного источника. Опыт осуществлялся следующим образом. В толстой эбонитовой пластинке Н (рис. 31) высверливались два отверстия: R и L. Отверстие R служило для откачки воздуха. Через отверстие L острие тонкой металлической проволочки К освещалось ультрафиолетовыми лучами, под действием которых освобождались фотоэлектроны. На острие подавался отрицательный потенциал (оно служило катодом). Напротив острия находилось маленькое отверстие, закрытое тонкой алюминиевой фольгой А, которая служила анодом и одновременно источником рентгеновских лучей, которые образовались в результате ударов о нее фотоэлектронов; фольга являлась также нижней пластиной конденсатора. Верхняя его пластина В имела окошко для наблюдения за висмутовой пылинкой W, помещенной в конденсаторе и находящейся в равновесии. Наблюдения показали, что при соответствующих условиях, когда число рентгеновских импульсов, испускаемых малым участком фольги А, было порядка 103 в секунду, пылинка теряла отдельные электроны через 20—40 мин. Такой результат нельзя было объяснить с точки зрения волновой теории света, согласно которой рентгеновские импульсы в данном случае должны излучаться в виде сферических волн. Невозможно предположить, что в течение 20— 40 мин электроны пылинки накапливали определенную энергию, которая затем сразу отдавалась одному из них, который и выбрасывался из пылинки. Наоборот, квантовая теория света легко объяснила этот опыт. Световые кванты летят по всем направлениям, и только часть из них случайным образом попадает на какой-либо электрон пылинки, который поглощает энергию данного кванта и выбрасывается из нее. Таким образом, в целом ряде исследований были получены новые подтверждения гипотезы Эйнштейна о квантовых свойствах света. Теперь всем было ясно, что световое излучение обладает и корпускулярными и волновыми свойствами. С другой стороны, становилось все более и более очевидно, что этот корпускулярно-волновой дуализм светового излучения нельзя объяснить с позиций классической физики. Требовались новые понятия, новые представления и новый язык, для того чтобы физики могли осмыслить этот дуализм. Этот язык появился несколько позже, вместе с открытием и развитием квантовой механики. 1Whittaker E. A. history of the theories of aether and electricity. The dassikal theories, 1951; p. 367—368 2Михельсон В. А. Собр. соч. Т. I, М., Изд-во «Новый агроном», 1930, с. 175. 3Wien W. Ann. Phys., В. 58, 1896, S. 662. 4Rау1еіgh J. Phil. Mag. (5), vol. 49, 1900, p. 539. 5Планк М. Избранные труды, с. 659. 6Планк М. Избранные труды, c. 258. 7Лоренц Г. Теория электронов и ее применение к явлениям света и теплового излучения. М., Гостехиздат, 1953, с. 127. 8Умов Н. А. Собр. соч. М.—Л., Гостехиздат, 1950, с. 503. 9Рlаnсk М, Verhandl. Deutsch, phys. Ges., В» J3, 1911, 8. 188. 10Планк М. Избранные труды, с. 325. 11Планк М. Избранные труды, с. 608. 12Die Theorie der Strahlung und der Quanten. Berlin, 1914, S. 94. 13Эйнштейн А. Собрание научных трудов. Т. III, с. 134. 14Debye P. Ann. Phys. В. 39, 1912, S. 789. 15Эта теория затем была изложена Борном в монографии «Динамика кристаллической решетки» (1915). См. русский перевод в кн.: Борн М. и Гепперг-Мейер М. Теория твердого тела. М.—Л., ОНТИ, 1938. 16Томсон Дж. Дж. Электричество и материя. М.—Л., 1928, с. 46—47. 17Эйнштейн А. Собрание научных трудов. Т. Ill, c. 93. 18Эйнштейн А. Собрание научных трудов. Т. III, с. 164. 19Эйнштейн А. Собрание научных трудов. Т. III, с. 194. 20Лоренц Г. А. Старые и новые проблемы физики. М., «Наука», 1970, с. 81. 21Милликен Р. Электрон, его изолирование, измерение и определение некоторых свойств. М., 1923, с. 182—183. 22Joffe A., DobronrawovN. Z. Phys., В. 34,1925, S. 889. |
загрузка...
