Р. А. Симонов. Учебные задачи для абака по пересчету натуры на деньги русской правды
|
Речь идет о дополнительных статьях 49—65 сельскохозяйственного содержания, встречающихся в Карамзинской группе списков Русской Правды Пространной редакции1. Б. А. Рыбаков первый верно поставил вопрос об их учебном назначении. Он обратил внимание на невероятность гигантского дохода, который должна была принести маленькая вотчина, если считать реальными данные статей-задач. В то же время последние имеют выраженный вычислительный характер, сводящийся к расчету стоимости приплода от скота, пчел, некоторых видов сельскохозяйственной продукции за 9, 10 или 12 лет, оплаты труда и пр. Все цены указаны в гривнах, ногатах и резанах, а итоговые суммы — в гривнах или в гривнах и резанах. Аналогичных текстов в литературе соседних народов не найдено. Б. А. Рыбаков высказал мнение, что статьи-задачи предназначались для обучения будущих тиунов, волостелей пересчету натуры на деньги2.
Точка зрения Б. А. Рыбакова расходится с принятой у историков математики. Так, известный советский ученый академик АН УССР Б. В. Гнеденко считает, что статьи-задачи Русской Правды «едва ли имели какое-либо практическое значение ... они удовлетворяли духовные потребности числолюбцев»3. Так думать заставляют огромные числа, порядка сотен тысяч, которые задавались условиями некоторых задач, а также необходимость производить действие деления при их решении. Делением, особенно многозначных чисел, в средние века овладевали немногие4. В древнерусских же задачах надо было, например, разделить число 360 446 на 50, чтобы получить стоимость шерсти, настригаемой с отары за 12 лет. Вот почему историки математики справедливо полагали, что тексты задач составлены выдающимся мастером в области древнерусской арифметики. Но если он это делал не для себя или себе подобных числолюбцев, а для обыкновенных учащихся, усваивавших навыки в пересчете натуры на деньги, то между ними и текстом задач должно было находиться какое-то вспомогательное средство, которое достаточно просто, как бы автоматически давало для заданного числа предметов сельскохозяйственного производства (овец, шерсти, меда, коров, масла и пр.) их денежную стоимость. Сейчас такого рода устройства имеются, это различного рода компьютеры. Для любого заданного числа ЭВМ по команде, соответствующей конкретной цене (1 гривна, 3 ногаты, 10 резан и пр.), молниеносно выдаст ответ о стоимости. Нужно только ввести в машину соответствующую программу (см. Приложение). Возможно ли было нечто подобное на Руси? «Как вычисляли авторы математических статей «Правды Русской», неизвестно»,—писал в 1968 г. один из ведущих советских историков математики А. П. Юшкевич5. Принятое в 1976 г. В. К. Кузаковым верное исходное положение, что для решения статей-задач «при всех математических операциях употреблялись специальные счеты», соседствовало с отрицательным заключением: «Все же мы не знаем, каким образом проводились тогда подобные операции»6. На такое неутешительное положение в решении проблемы указывал в 1978 г. В. В. Мавродин: «... В древней Руси люди производили сложные вычисления, но как производили счет, остается неизвестным, так как записывался только итог. Возможно, что существовали абаки или аналогичные приспособления для счета»7. Автор настоящей статьи примерно с 1970 г. работал над проблемой о древнерусском вычислительном средстве, для которого предназначались статьи-задачи Русской Правды8. Теперь эту проблему можно считать решенной, изложению чего посвящена настоящая статья. Прежде всего следовало выявить тип абака, в наибольшей степени соответствующий всей совокупности данных о наглядно-инструментальном счете, относящихся к русским и соседним землям. В результате было установлено, что с наибольшей вероятностью на Руси мог употребляться тип абака, описание которого дано Я. Накциановичем в 1759 г., по-видимому, на основе бытовавшего в народной среде славянского и литовского населения9. «Запись» чисел на таком абаке производилась на горизонтальных уровнях. На нижнем откладывались единицы, далее (снизу вверх) шли десятки, сотни, тысячи и т. д. На каждом уровне располагались пятерка и пять разрядных единиц. Я. Накцианович их обозначал одинаковыми кружочками, кружочек-пятерка находился слева на некотором расстоянии от кружочков-единиц. Из литературы известно, что при счете на архаических абаках использовались камешки, бобы, плодовые косточки и другие мелкие предметы, а также специальные жетоны. По данным иностранцев Г. Штадена (вторая половина XVI в.) и А. Олеария (первая половина XVII в.), в России применялись для счета вишневые и сливовые косточки в россыпи. Для удобства дальнейшего изложения будем считать, что в домонгольской Руси полуразряды (пятерки) откладывались сливовыми косточками, а единицы— вишневыми. Счет мог вестись на любой ровной поверхности: столе, лавке, полу, земле. Изложенные данные о структуре древнерусского абака получили одобрение в научной печати и стали предметом дальнейшего углубленного изучения10. Все виды архаического абака, как правило, программировались в определенной денежной системе. Судя по статьям-задачам Русской Правды, в древнерусском абаке должна быть запрограммирована древнейшая система: 1 гривна кун = 20 ногатам = 50 резанам, что могло быть сделано несколькими способами. Следовало установить, каким именно. Если исходить из того, что основной или базовой единицей счета выступала гривна кун, то вишневой косточкой (0) будет обозначаться одна гривна на самом нижнем уровне, десяток, сотня, тысяча и т. д. гривен на последующих уровнях, а сливовой (0) —пять гривен на нижнем уровне, 50, 500 и т. д. гривен на последующих уровнях. Как считали на таком абаке, покажем на примере задач Русской Правды, в которых цены указаны в одну гривну («третьячные» кобылы — задача № 54 и коровы — № 55, сено — № 64), две (взрослые коровы — № 56, оплата труда батрачек —№ 65) и три (взрослые кобылы — № 54,55) гривны. 
При цене в одну гривну достаточно записать исходное число в системе именованного абака. Например, по данным задачи 64, стоимость 60 стогов сена можно найти, отложив соответствующее число — одной сливовой (50) и одной вишневой (10) косточками — на втором уровне абака, получим 60 гривен (см. схему 2). При цене в две гривны достаточно удвоить исходное число. Например, по данным задачи № 65, две батрачки, получая каждая по гривне в год, за 12 лет заработали 24 гривны. Исходное число 12, отложенное одной вишневой косточкой на втором уровне и двумя на первом, при удвоении обозначится двумя вишневыми косточками на втором уровне (20) и четырьмя на первом (4), что в совокупности дает искомый результат — 24 гривны (см. схему 3). 
При цене в три гривны нужно утроить заданное число, т. е. к исходному значению прибавить удвоенное. Например, по данным задачи № 54, стоимость 32 лошадей можно найти, сложив исходное число с удвоенным 64, что даст 32+640 96 гривен (см. схему 4). При цене в половину гривны (свиньи — 51, 53, «лоньские» коровы и быки — 56, пчелиный рой с медом — 57) для получения искомого результата достаточно раздвоить исходное число. Например, по данным задачи № 56, стоимость четырех коров и быков можно найти, «записав» указанное число 4 на нижнем уровне абака и раздвоив его, получится 2 гривны (см. схему 5). Если исходное число четное, то при раздвоении число гривен будет целым, как в приведенной задаче. Если исходное число нечетное, то при раздвоении, помимо целого числа гривен, еще будет одна полугривна. Следовательно, основную часть абака необходимо дополнить еще одним уровнем для дробных долей гривны, где разрядной пятеркой будет полугривна, а единицами — пятки резан (5 резан X 5 = 25 резан = 1 полугривна) (см. схему 6). 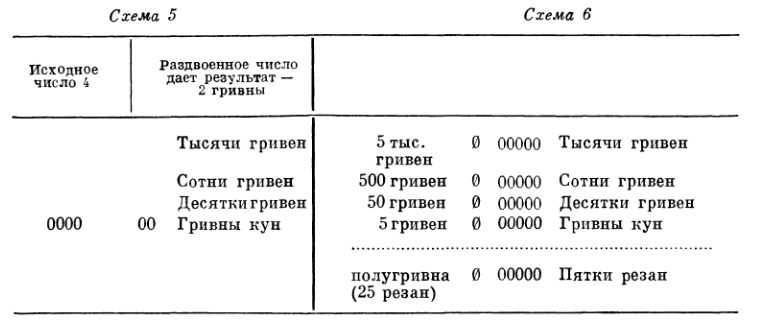
Необходимость такого дополнения подтверждается задачами, в которых цены указаны в 10 резан (бараны —49, козлы—50, масло —56), 6 ногат (овцы — 49, козы — 50, вепри — 52, 53, жеребята — 54) и 30 резан («лоньские» жеребцы —54 и кобылы —55). При цене в 10 резан исходное число достаточно «записать», удвоить и прочесть полученный результат в системе абака, дополненного новым уровнем (полугривна — пятки резан). Например, стоимость 90111 баранов , по цене 10 резан (задача № 49) можно найти, удвоив это число (см. схему 7)11. При цене в 6 ногат, т. е. 15 резан, стоимость 90112 овец (задача № 49) находится утроением, т. е. сложением указанного числа овец с его удвоенной величиной (см. схему 8). При цене в 30 резан результат, полученный для цены в 15 резан утроением, нужно еще и удвоить. 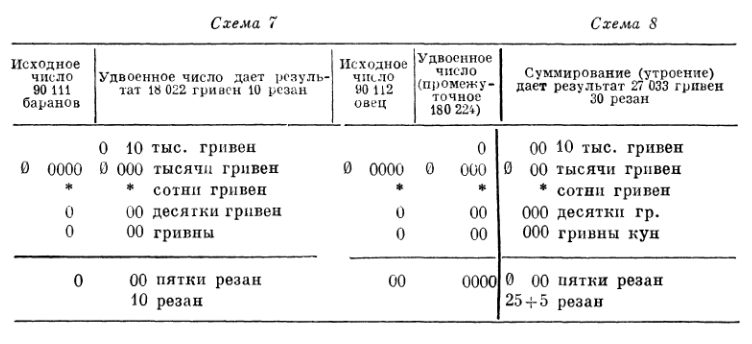
Остается нерассмотренным только один случай — определение стоимости натуры при цене в одну резану (руно — 49, сыр — 56). Для соответствующих вычислений абак требуется дополнить еще одним уровнем с пятеркой-ногатой и разрядными единицами, по величине равными половинам резан (см. схему 9). Тогда для получения, например, стоимости руна, состриженного с 360 446 овец и баранов, надо удвоить это число, записанное в системе абака, дополненного двумя уровнями, что дает искомое значение — 7208 гривен 46 резан (см. схему 10). Таким образом, древнерусский абак для пересчета натуры на деньги должен был иметь две части — основную (верхнюю) и дополнительную (нижнюю) (см. схему 9). Основная (верхняя) предназначалась для гривен (единиц, десятков, сотен и т. д.), дополнительная (нижняя) — для ее долей. Причем эти доли укладываются как в общую пятерично-десятеричную структуру абака, так и в существовавшие материальные (в виде монет) или счетные единицы древнерусской денежной системы. Полугривна это десять ногат, или 25 резан; ногата — первоначально куфический дирхем, вес которого равнялся 3,41 г; полурезана, равная 7юо гривны, совпадала с веверицей, выделенной Н. П. Бауером на основе данных Русской Правды Краткой редакции12. На таком абаке все задачи Русской Правды решаются однотипно: путем средневекового арифметического действия удвоения или утроения (сложения первоначального числа с удвоенным), а также действия раздвоения (в одном случае цены в полугривну). 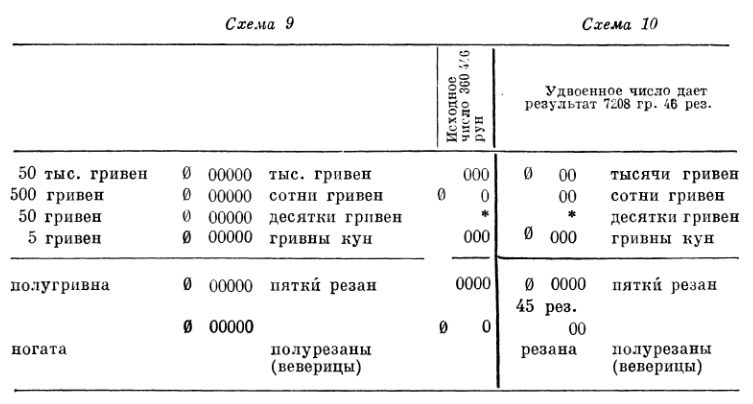
Основной учебной проблемой, которая вставала перед древнерусскими педагогами-математиками, было научить правильно выбирать базовый (нижний) уровень для записи исходного числа. В таком случае становится ясен методический смысл задач, в которых цена указана в одну гривну. Априори эти задачи вызывают недоумение, так как для их решения не нужен абак, ибо очевидно, что «а» предметов ценой в одну гривну будут стоить «а» гривен. Однако с учетом структуры абака, имеющего, кроме основной части, еще и дополнительные уровни, будет понятно, что необходимы задачи, отрабатывающие навык по различению уровней. Точнее, по распознаванию основной части абака, начинающейся уровнем, содержащим единицы и пятерку гривен. Таковыми и являются задачи с ценой в одну гривну. Методическими целями обусловлена номенклатура цен в целом, которые, как давно замечено учеными, не совпадали с реальными стоимостями натуры. Цены в две гривны, десять и одну резану необходимы для отыскания стоимости действием удвоения на основной части абака (см. схему 3), с одним (см. схему 7) и двумя (см. схему 10) дополнительными уровнями. Цены в 3 гривны и 6 ногат необходимы для отыскания стоимости действием утроения на основной части абака (см. схему 4) и с одним дополнительным уровнем (см. схему 8). Все итоговые значения получаются на том же уровне абака, на котором «записываются» исходные. В этом свете обращает на себя внимание указание только четных значений исходных чисел в задачах на раздвоение (при цене в полугривну). В этом случае обеспечивается соблюдение указанного правила. Если бы исходные числа были нечетными, то оно нарушалось: конечный результат располагался на один уровень ниже исходного числа. Задачи, кроме содержащих цену в 30 резан, связаны с выполнением одной элементарной вычислительной операции: удвоения, утроения, раздвоения. Цена в 30 резан позволяет показать, что путь к овладению более сложными приемами пересчета натуры на деньги связан с последовательным применением элементарных операций (в данном случае утроения и удвоения). Наличие огромных чисел в некоторых статьях-задачах также объясняется особенностями обучения счету на архаическом абаке. При обучении вычислениям на современных счетах максимальная величина чисел обусловлена конструкцией прибора: размерами рамы и количеством вделанных прутьев. Архаический абак лишен такого преимущества, о его «длине» учащиеся могут судить, упражняясь с максимальными числами. Последние показывают, что счет на древнерусском абаке в учебных целях велся до сотен тысяч. Профессиональные вычислители выполняли действия с еще большими числами, порядка нескольких десятков миллионов, о чем свидетельствует «Учение им же ведати человеку числа всех лет» Кирика Новгородца (1136 г.). Древнерусский абак становится такой же реальностью, какой стали берестяные грамоты, и, так же как они, абак служит важным дополнительным свидетельством высокого уровня грамотности на Руси, грамотности вычислительной. Такое заключение приобретает особую актуальность в свете предстоящей компьютеризации советской образовательной системы, рассматривающейся как «вторая грамотность». «Средневековая компьютеризация» в свое время, возможно, сыграла важную роль в развитии культуры Руси. Этот вопрос еще предстоит всесторонне исследовать. Однако уже сейчас несомненна перспективность изучения роли абака как рационализирующего фактора в формировании древнерусской денежной системы. Несмотря на известную изменяемость в зависимости от регионов функционирования и исторической эпохи, общенациональная русская денежная система, сложившаяся в XV в., сохранила пятерично-десятеричную основу, восходящую к денежной системе Русской Правды13. ПРИЛОЖЕНИЕ Программа на алгоритмическом языке ФОРТРАН-IV для ЕС ЭВМ (составлена канд. техн. наук Т. Г. Дацко) по пересчету натуры на деньги на материале статей- задач Русской Правды. Использована на практических занятиях по курсу «Машинная обработка экономической книготорговой информации» в Московском полиграфическом институте. 
1 Правда Русская/Под общ. ред. Б. Д. Грекова. Т. 1. Тексты. М., 1950. С. 352-354, 377-380; Т. 3. Факсимильное воспроизведение текстов. М., 1963. С. 401-406, 444- 450. 2 Рыбаков Б. А. Просвещение//Очерки русской культуры XIII-XIV вв. М., 1970. Ч. 2: Духовная культура. С. 180. 3 Гнеденко Б. В. Очерки по истории математики в России. М.; Л., 1945. С. 20. 4 «Тот, кто оказывался в состоянии понимать деление, признавался чуть ли не гением и ему давали почетный титул - «доктора абака», вроде нашего «доктора математики» или «доктора медицины». Нормальным, заурядным детям нечего было и мечтать о таком трудном, мудреном действии, и они скромно ограничивались сложением и вычитанием, с придачей таблицы умножения» (Беллюстин Б. [К]. Как постепенно дошли люди до настоящей арифметики. М., 1941. С. 99). 5 Юшкевич А. П. История математики в России до 1917 г. М., 1968. С. 17. 6 Кузаков В. К. Очерки развития естественнонаучных и технических представлений на Руси в X-XVII вв. М., 1976. С. 112. 7 Мавродин В. В. Научные знания//Советская историография Киевской Руси. Л., 1978. С. 259. 8 Симонов Р. А. О методологии изучения математики Древней Руси//СА. 1980. № 3. С. 254-257; Он же. Древнерусские математические знания и их значение для исторической науки: Автореф. дис. ... д-ра ист. наук. М., 1973. С. 16-20; Он же. О проблеме наглядно-инструментального счета в средневековой Руси // СА. 1975. № 3. С. 82-93; Он же. Математическая мысль древней Руси. М., 1977. С. 44-74; Он же. «Запись» чисел на древнерусском абаке // Древняя Русь и славяне. М., 1978. С. 413-420; Он же. О вычислительной арифметике // Естественнонаучные представления древней Руси. М., 1978. С. 63-73; Он же. Кирик Новгородец - ученый XII в. А., 1980. С. 58—74; Кузнецова В. С., Симонов Р. А. Об умножении на древнерусском абаке//Естественнонаучные знания в древней Руси. М., 1980. С. 12 — 15; Симонов Р. А. Древнерусский абак//Тез. докл. сов. делегации на V Междунар. конгр. славян, археологии. М., 1985. С. 165. 9 Nakcyanowicz J. Praelectiones mathematicae ex Wolfianis elementis adornatae. Yilnae, 1759. P. 149-151. 10 Виленчик Б. Я. Новые доказательства существования русского архаического абака//СА. 1984. № з. с. 59-65. 11 Звездочкой в схемах 7, 8, 10 обозначается пропуск десятичного разряда, соответствующий в современной числовой записи нуля. 12 Бауер Н. П. Денежный счет Русской Правды//Вспомогательные исторические дисциплины. М.; Л., 1937. С. 229; Янин В. Л. Денежно-весовые системы русского средневековья: Домонгольский период. М., 1956. 13 Это утверждение справедливо и для новгородской денежной системы XV в., несмотря на кажущееся ее отличие от денежной системы Русской Правды. См.: Янин В. Л. «Память, как торговали доселе новгородцы»: (К вопросу об эволюции новгородской денежной системы в XV в.) // Вспомогательные исторические дисциплины. Л., 1985. Вып. 16. С. 98-114; Симонов Р. А. Модель новгородского абака XV в.//Там же. С. 114-123. |
загрузка...
