X. Обзор сочинения «Геометрия»
|
К какому из воззрений на построение начал геометрии примыкал Лобачевский? Прежде всего нужно сказать, что Лобачевский никогда не благоговел перед Евклидом. Во введении к первому же опубликованному им сочинению — «О началах геометрии» — он говорит: «Кто не согласится, что никакая математическая наука не должна бы начинаться с таких темных понятий, с каких, повторяя Евклида, начинаем мы геометрию?»
Человек своеобразного, оригинального склада ума, Лобачевский всегда искал своих путей всюду, куда направлялась его мысль. И общая тенденция, отчетливо проходящая через все его небольшое первое сочинение, есть стремление порвать со старыми классическими традициями, искать других, собственных путей для построения основ геометрии. И, конечно, в этой сложной задаче построения всей системы геометрии молодой Лобачевский еще не добился большого успеха; но и здесь он шел тем путем напряженного искания, который потом привел его к замечательным открытиям. Однако именно это стремление освободиться от оков традиции, несомненно, было главной причиной того осуждения, которое встретила первая же его работа. Влияние Даламбера отчетливо проникает все сочинение; но Лобачевский идет дальше Даламбера, он гораздо глубже перестраивает геометрию, нежели это сделали Лежандр и Лакруа. Прежде всего влияние Даламбера сказывается на самом определении геометрии. В противоположность установке Евклида, он считал, что «Геометрия есть часть чистой математики, в которой предписываются способы измерять пространство». Эта метрическая точка зрения была прогрессивной для того времени: она была отчетливо направлена против обучения основам геометрии по чисто формальной системе Евклида, отрывающей геометрию от каких бы то ни было ее приложений, сводящей ее только к логической концепции. Не может быть сомнения в том, что это был уже переход от идеалистических тенденций верного ученика Платона к материалистической установке. Правда, это был еще явно узкий механический материализм, который и раньше имел немало сторонников. Ярким представителем его был Даламбер. Однако для студенческой аудитории в десятых годах прошлого столетия это был уже недостаточно широкий взгляд, не оставлявший в геометрии ничего, кроме метрики, и притом взгляд для той эпохи уже не вполне современный. Со времени опубликования плана Даламбера прошло уже 60 лет; в это время именно во Франции шло возрождение синтетических методов; Монжем уже была опубликована «изобразительная», или, как теперь говорят, «начертательная» геометрия, дисциплина, в которой метрические задачи играют доминирующую роль, но которая имеет уже существенно новые задачи. Еще раньше появилась «геометрия положения» Карно. Целая школа геометров развивала эти идеи в «Анналах» Жергона, а в 1822 г. появился знаменитый трактат Понселе; говорить в ту пору студентам, что геометрия занимается исключительно измерением пространственных протяжений, было односторонним и безусловно уже несовременным. Очевидно, в то время научные течения медленно докатывались до далекой Казани. Во всяком случае на этой метрической точке зрения Лобачевский стоит твердо. Вся книга разбивается на тринадцать глав, из которых десять как по названию, так и по содержанию посвящены измерению тех или иных геометрических величин (измерению линий, углов, телесных углов, треугольников, призм и т. д.), а остальные три подготовляют для этого необходимые средства (учение о перпендикулярных прямых, о равенстве треугольников, о параллельных линиях). И все содержание геометрии Лобачевский делит на лонгиметрию, планиметрию и «штереометрию» именно в том понимании этих терминов, на котором настаивает Даламбер (измерение длин, измерение площадей, измерение объемов), даже более решительно это отмечая. В этой своей метрической точке зрения Лобачевский идет так далеко, что угол он определяет только как численное значение дуги (в градусах или радианах), содержащейся между его сторонами; и эту точку зрения он сохраняет позже во всех своих сочинениях. Обращаясь теперь к общей системе изложения, нужно сказать, что «химерическая» схоластическая строгость Лобачевскому совершенно чужда. Следует ли он в этом отношении Даламберу или в воззрениях Даламбера он нашел опору для своих собственных взглядов на этот предмет, — но аксиом Лобачевский не приводит нигде, ни в «Геометрии», ни в последующих сочинениях. «Геометрические исследования» он начинает пятнадцатью предложениями, которые принимает за исходные или известные; большинство из них представляет собой теоремы, доказательства которых общеизвестны, другие обычно входят в определения или аксиомы; Лобачевский не делает между ними различия. Даже в «Новых началах», в этой фундаментальной попытке построения всей системы геометрии, Лобачевский не приводит аксиом. Он хорошо знает цену аксиоматике своего времени и решительно предпочитает вовсе не давать «химерического» обоснования геометрии; для подлинного же обоснования геометрии именно он позже и заложил надежный фундамент. Из основных понятий геометрии Лобачевский в «Новых началах» выдвигает на первый план «прикосновение тел» и делает это понятие точкой отправления при построении всей геометрии, развертывая эту идею в целую систему. Первый замысел этой системы мы видим уже здесь, в «Геометрии», в первых же строках; Лобачевский, таким образом, пришел к нему очень рано. Он еще не пытается сделать это понятие краеугольным камнем при построении всей геометрии; но он уже начинает изложение геометрии с этого понятия, которому, как увидим, он позже придает основное значение. Одним из коренных вопросов в деле построения элементарной геометрии является та роль, которая при этом должна принадлежать движению. Евклид отводит движению незначительное место: установив при помощи движения равенство треугольников по двум сторонам и углу между ними (предложение 4 книги I) и по трем сторонам (предложение 8 книги I), Евклид в дальнейшем тщательно избегает пользоваться движением, заменяя его формальными рассуждениями, основанными на условиях равенства треугольников. Даламбер, в противовес этому, предлагает пользоваться движением и, в частности, наложением, как основным методом геометрического доказательства. Лежандр в некоторой степени следует этому указанию. Лобачевский идет по этому пути решительнее, чем это делал кто-либо до него или даже в ближайшие годы после него. Всякое сопоставление в смысле установления условий равенства или неравенства Лобачевский проводит, сводя соответствующие фигуры в пространстве. Позднее Гельмгольцем, Софусом Ли и Клейном движение было признано основной характеристикой геометрии (см. главу XXXI). Правда, Лобачевский не формулирует законов движения; но, как уже сказано, он избегает всякой аксиоматики. Построение метрики в геометрии всегда связано с большей или меньшей ее арифметизацией, и такая арифметизация Лобачевским действительно проводится. Спор о геометрической или арифметической теории пропорций, таким образом, решается сам собою: отношение для Лобачевского всегда есть число. Так как измерение приводится к нахождению отношения двух значений величины (двух «коликих»), то Лобачевский в первой же главе приводит евклидов алгорифм для разыскания общей меры; получающееся в результате отношение он выражает непрерывной дробью, наиболее отражающей геометрический процесс. Случай несоизмеримости играет, как известно, в этой арифметизации, в этом стремлении выразить отношение двух отрезков числом особую роль. Его обработка как с теоретической, так и с педагогической стороны служила предметом многостороннего обсуждения и споров со времен Евклида и, можно сказать, вплоть до наших дней. Трудность заключается здесь в двух моментах: Во-первых, в самом определении несоизмеримого отношения, т. е. иррационального числа; во-вторых, в учении о пропорциональных величинах разного рода, т. е. в доказательстве равенства или неравенства иррациональных чисел или несоизмеримых отношений. Евклид сосредоточивает внимание на второй проблеме: он определяет не самое отношение, которое как число для него вовсе не существует, а только условия, при которых два отношения равны или не равны; для этого он и излагает своеобразную теорию пропорций. Даламбер также игнорирует первую проблему. Но он молчаливо всегда постулирует существование числа, выражающего отношение двух несоизмеримых значений одной и той же величины. Доказательство равенства несоизмеримых отношений он рекомендует всегда производить приведением к абсурду; Лежандр и Лакруа так это неизменно и выполняют. Лобачевский вообще не любит доказательств от противного; к этому приему он прибегает очень редко, скорее для сокращения рассуждения, чем для придания ему строгости. Его аналитический ум всегда ищет прямого доказательства каждой истины. В современной математике, в теории иррациональных чисел или несоизмеримых отношений внимание сосредоточивается на первой проблеме. В той или иной форме несоизмеримое отношение всегда определяется совокупностью его последовательных приближений, и тогда равенство несоизмеримых отношений заключается в постоянном совпадении соответствующих приближений. К этой последней точке зрения, по существу, приближается и Лобачевский. Строгий, неизменно последовательный эмпирик-материалист, он признает только, процессы, фактически выполнимые. Разыскивая отношение так называемым алгорифмом Евклида («Начала», VII2)> т. е. последовательным делением, он считает, что этот процесс заканчивается тогда, когда остаток перестает быть доступным нашим ощущениям. Он говорит (глава I): «Наконец не должно выходить остатку или, что все равно, быть так малу, что чувства не могут его давать знать, того менее орудие мерять». В этот момент процесс обрывается, отношение представляет собой рациональное число, выражаемое непрерывной дробью.. Для Лобачевского, таким образом, существуют только рациональные приближенные отношения, выражаемые с любой доступной нам точностью. Вопрос об иррациональных отношениях как бы отпадает; при установлении пропорциональности Лобачевский всегда доказывает, что соответствующие отношения будут равны, какова бы ни была доступная нам точность. По существу, это, конечно, лишь иное выражение той же идеи, лежащей в основе современной постановки вопроса; немногое нужно изменить в формулировках Лобачевского, чтобы к ним присоединился современный математик. Для измерения нужны единицы меры. Лобачевский вводит метрическую систему с ее децимальными подразделениями, сохраняя также центезимальное деление прямого угла. Как, может быть, никто другой в России того времени, оп понимал значение единого стандарта и упрощенной техники арифметических вычислений. И с первого же сочинения, предназначенного для печати, он выступает со своими своеобразными взглядами, не страшась «крика беотийцев». Очень характерно, что всюду он выступает борцом за несомненно прогрессивную точку зрения. Лобачевский с самого начала делит геометрию на лонгиметрию, планиметрию и стереометрию, однако в метрическом (даламберовом) понимании этих терминов (измерение длин, площадей и объемов). Но во всем, что не составляет предмета прямых измерений, Лобачевский не отделяет предложений плоской геометрии от аналогичных предложений, относящихся к пространству. Так, уже во II главе он рядом с кругом рассматривает шар и сферу. И здесь уже лежат зародыши той общей системы геометрии, которую он строит в «Новых началах». В III главе — «О перпендикулах» — он рассматривает взаимное расположение плоскостей, а в IV главе рядом с измерением прямолинейных углов рассматривает измерение телесных, рядом с многоугольниками рассматривает многогранники. Лобачевский, таким образом, уже в начале века стоял на позиции фузионизма, которую в конце века защищали многие математики и педагоги. Фузионистскую точку зрения при построении начал геометрии нельзя считать общепризнанной; она имеет много противников; в то время она была еще совершенно нова; мы не знаем автора, который до Лобачевского становился бы на эту точку зрения. Между тем, именно при повторном обзоре геометрии проводить эти сближения двумерных и трехмерных соотношений безусловно целесообразно. Но Лобачевский имеет при этом и своеобразную, очень характерную для его дальнейшего творчества цель, о которой скажем ниже. Во всяком случае, и в этом сказывается та оригинальность системы, которая так характерна для Лобачевского вообще, для этого сочинения в частности. Очень характерным для всякого курса геометрии является изложение вопроса об измерении длины окружности, площади круга, поверхностей и объемов круглых тел. По существу, есть три способа изложения этого вопроса. Первый заключается в том, что предложение формулируется и доказывается от противного: так Евклид доказывает, что треугольные пирамиды, имеющие равновеликие основания и равные высоты, равновелики; этого же метода придерживается единообразно и Лежандр. Второй способ заключается в применении принципа Кавальери в той или другой форме; так доказывают ту же теорему о равновеликости пирамид Безу и Фусс. Третий способ есть метод прямого вычисления переходом к пределу: это — метод исчерпывания, как его понимал еще Архимед; это — метод интегрирования, как его понимали Лейбниц и Ньютон. В этом последнем порядке идей всегда проводит вычисления Лобачевский, и притом обыкновенно методом, который ближе всего подходит к интегрированию; его вычисление объема шара есть элементарное вычисление интеграла 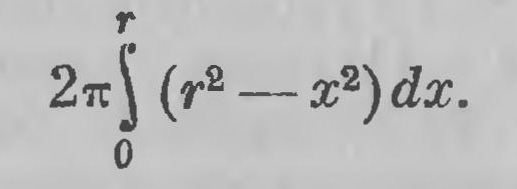
Очевидно, сделать ясным для своих слушателей, что здесь мы имеем дело с чистым интегрированием, и составляло задачу, которую ставил себе Лобачевский. Многие педагоги в наши дни особенно настойчиво отстаивают такое изложение учения об измерении площади круга и объема шара. Остановимся еще на том принципе, которому следует Лобачевский при расположении материала. Академик Гурьев в предисловии к своей книге говорит, что система изложения может быть расположена «либо соображенная с началами, или соображенная с предметами». Расположение, сообразованное с началами, восходит от простейших понятий и образов к более сложным, рассматривая прямые линии, углы, треугольники, четырехугольники, многоугольники, окружности и т. д. При изучении более сложного объекта в этой системе можно пользоваться заранее подготовленными установленными свойствами более простых объектов. Изложение, сообразованное с «предметами», заключается в том, что каждый раз в соответствии с основной задачей приводятся те подсобные предложения, которые здесь именно нужны. С точки зрения такого подразделения, если считать его правильным, система Евклида «сообразована с началами» (так Гурьев и утверждает), система Лобачевского «сообразована с предметами». Постоянно пользуясь непосредственно движением, Лобачевский отодвигает учение о равенстве треугольников до V главы и излагает даже учение о правильных многоугольниках и многогранниках без его помощи. Не всегда это дает хорошие результаты. Конечно, наложение делает многие доказательства более наглядными; но нередко это вызывает длинноты и повторения. К числу вопросов, значительно отодвинутых в изложении, принадлежит и учение о параллельных линиях. Кто знает дальнейшее направление работ Лобачевского, тому ясно, какую роль учение о параллельных линиях играет уже в «Геометрии»; мы к этому возвратимся ниже; здесь уже отчетливо намечаются установки, которые приведут в дальнейшем к отходу от геометрии Евклида. Учение об измерении прямолинейных фигур и многогранников без инфинитезимальных приемов составляет вторую часть геометрии; по существу, оно выполнено по плану Даламбера, но своеобразно (главы VI—IX). Наконец, третью часть книги составляют те измерения, которые выполняются при помощи интегрирования. И этим путем, прямым интегрированием, Лобачевский ведет вычисления, начиная с площади круга, с .объема пирамиды и кончая объемом шара. Таким образом, ясно, что Лобачевский при составлении «Геометрии» не считал систему Евклида пределом совершенства и искал путей построения основ геометрии на новых началах. И не только в этих общих чертах, не только в систематизации и расположении материала, но и в каждом рассуждении можно видеть оригинальную мысль, стремящуюся отойти от традиций и провести доказательство своеобразно, по-новому. И это не просто желание быть оригинальным во что бы то ни стало: всюду и всегда можно видеть те принципиальные мотивы, которые побуждали автора идти не традиционным, а своеобразным путем. Иногда его доказательства прерываются рассуждениями того или другого комментатора Евклида; не всегда они удачны, но всегда можно усмотреть ту цель, которая руководила автором при выборе системы, метода рассуждения. Наиболее характерная черта всего сочинения — это искание новых путей в построении начал геометрии, стремление по крайней мере в этом обзорном курсе отойти от укоренившихся, веками утвержденных традиций, которые выдающиеся французские геометры не счи> тали лучшими путями построения системы геометрии даже в учебной книге. Эти искания занимали Лобачевского уже давно; как мы знаем, в 1819 г. они сложились в форму сочинения «Основание геометрии». В 1823 г. они были оформлены в виде учебной книги, которую Лобачевский представил к напечатанию. Мы очень подробно остановились на обзоре «Геометрии» потому, что не разделяем того мнения, которое высказывалось об этом сочинении устно и печатно. Утверждают, что это сочинение слабое, и слышатся даже нотки колебания, не прав ли был до некоторой степени Фусс. Это совершенно неправильно. Сочинение имеет дефекты; оно еще недостаточно обработано. Но кто изучал работы Лобачевского, тот несомненно признает, что в этом первом его произведении он уже виден весь, со всем его своеобразием, упорным нежеланием итти по шаблонному пути, его исканиями и замыслами. Более того, печать тщательного размышления над теми вопросами, которые позднее привели Лобачевского к новой геометрии, явно лежит уже на этой его работе. Об этом речь будет идти ниже. Расхождение между Фуссом и Лобачевским в существе своем коренилось в том, что Фусс принадлежал к школе Эйлера, Лобачевский — к школе Коши и Гаусса. И Эйлер, и Коши, и Гаусс были гениальными математиками; но в методологии, в оценке математических рассуждений, которые можно считать убедительными, Коши и Гаусс оставили Эйлера далеко позади. Это умонастроение, эта глубина и тонкость мысли, эта склонность выяснить все сомнения без остатка, не оставаясь в оковах традиций, все это, а не прямые соображения, относящиеся к теории параллельных линий, Лобачевский через Бартельса действительно унаследовал от Гаусса. И наследие это можно выразить известным афоризмом: Мудрец отличен от глупца Тем, что он мыслит до конца. В заключение необходимо еще указать, что учебник Лобачевского, хотя и не был одобрен Фуссом, и не был напечатан, все же служил в Казанском университете пособием для студентов. Н. О. Юферов, состоявший с 1822 г. магистром математики и физики, по поручению факультета, читал начинающим студентам курс геометрии. В своих проспектах он неоднократно указывает, что курс этот он читал по книге Лобачевского. |
загрузка...
