Наряду с универсальными построениями, характерными для ранней греческой науки «о природе», в VI—V вв. до н. э. возникли и некоторые более частные дисциплине, либо с самого начала развивавшиеся самостоятельно, либо постепенно отделившиеся от основного физико-космологического направления.
Историко-географические описания. Особой ветвью ионийской науки, возникшей почти одновременно с наукой «о природе», были историко-географические описания, материалом для которых служили мифы, народные предания, собственные наблюдения, рассказы и записи путешественников. Авторы этих описаний получили позднее общее наименование логографов. В числе наиболее ранних логографов традиция называет двух милетцев — Кадма и Гекатея. О первом мы не знаем ничего, кроме имени, что же касается Гекатея, жившего во второй половине VI в. до н. э., то он написал два больших сочинения: «Генеалогия» и «Обозрение Земли», от которых до нас дошел ряд отрывков. Уже сами их заглавия показывают, что одно из них имело по преимуществу исторический характер, а второе, интересующее нас в первую очередь, содержало описание известной к тому времени ойкумены (обитаемой области Земли). Оно состояло из двух частей, посвященных соответственно Европе и Азии, Следуя почину Анаксимандра. Гекатей приложил к нему географическую карту, на которой поверхность Земли была представлена в виде диска, омываемого со всех сторон Океаном. Центр диска оказался где-то в районе Эгейского моря. В больший реки — Дунай, Нил, Фасис (Рион) — Гекатей считал вытекающими из Океана (рис. 1). Геометрический схематизм Гекатея был подвергнут критике позднейшими географами, но для целей первой ориентировки он представлял известные удобства.
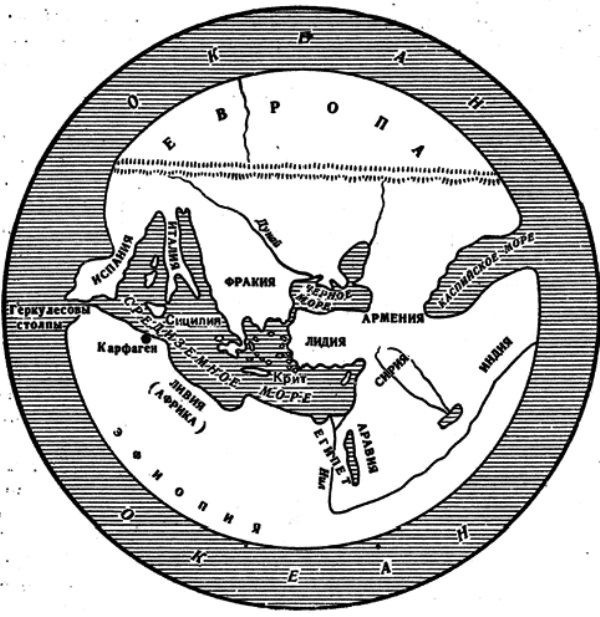
Рис.1. Карта мира по Гекатею
В V в. до н. э. во многих областях Эллады имелись логографы, описывавшие предания, обычаи и события соответствующего народа или государства. Из них наиболее известны имена Акусилая из Аргоса и Гелланика с острова Лесбос. Общую характеристику литературы этого рода дает Дионисий Галикарнасский (конец I в. до н. э.— начало I в. н. э.). Он сообщает, в частности, что в его время сочинения логографов еще не были утеряны и охотно читались. Причина их популярности заключалась, очевидно, в присущей им занимательности; многие из этих сочинений были, по-видимому, чем-то вроде сборников новелл, сравнительно слабо связанных друг с другом. Критикуя своих предшественников, историк Пелопоннесской войны Фукидид (конец V в. до н. э.) указывает, что они в своих сочинениях стремились скорее к тому, чтобы вызвать интерес у слушателей, чем к истине. Из этих слов, в частности, следует, что логографы имели обыкновение читать свои произведения перед более или менее многолюдной аудиторией, подобно тому
как рапсоды читали эпические поэмы.
Высшей точкой развития жанра историко-географической литературы явились знаменитые девять книг Геродота из Галикарнасса (ок. 480—425 гг. до н. э.). Геродот часто именуется «отцом истории», и, действительно, его монументальный труд стал первым классическим памятником исторической, науки. Однако наряду с чисто историческим материалом в его книгах содержатся описания многих стран, которые в большей или меньшей степени были известны грекам того времени. В этих описаниях мы находим массу ценной информации о природе этих стран, о населявших их народах, включая их образ жизни, обычаи, религиозные верования и т. д. В целом по книгам Геродота можно составить достаточно полное представление о географическом кругозоре греков середины V в. до н. э.
Геродот хорошо знал страны, непосредственно прилегавшие к Средиземному и Черному морям, но обо всем, что лежало за пределами этой области, он имел лишь весьма смутное представление. Например, ему было известно о существовании на востоке Индии, которая, согласно его описаниям, была полна диковин и изобиловала эолитом; за Индией же, по его словам, простираются пески и пустыня. Если о скифах Геродот сообщает достаточно полную и точную информацию, то сведения о странах и народах, находившихся к северу от Скифии (под которой подразумевалось северное Причерноморье между Дунаем и Доном), у него путаны и неправдоподобны. Почти все, что Геродот сообщает об Аравии, относится к области сказочных небылиц. С другой стороны, его описания Персии и Египта основаны па собственных наблюдениях и на информации, полученной им непосредственно на местах, поэтому долгое время они были важнейшим источником сведений об этих странах. Африканскую территорию к западу от Египта (Ливию) Геродот делил на две зоны: страну, населенную дикими зверями, а затем — бесплодную пустыню, о размерах которой у него не было определенного мнения.
После Геродота происходит обособление исторической науки и географии. Фукидид, Эфор и Феопомп (конец V—IV вв. до н. э.) выступают в качестве чистых историков. Что же касается дальнейшего развития географии, то о ней речь пойдет ниже.
Медицина. Медицину в силу ее сугубо прикладной направленности мы не можем считать наукой в собственном смысле слова. В древности она относилась скорее к разряду ремесел и была одной из самых старых профессий, первоначально сливавшейся с магией и колдовством. В рассматриваемую нами эпоху греческая медицина приняла уже вполне рациональный характер и, будучи тесно связана с опытом и наблюдением, оказала громадное влияние на развитие научных методов исследования.
Наиболее ранние сведения из области греческой медицины мы находим в поэмах Гомера. В «Илиаде» речь идет преимущественно о военной медицине, отличавшейся сравнительно высоким уровнем анатомических знаний и требовавшей, с одной стороны, хирургического искусства, а с другой — умения изготавливать и применять лекарственные снадобья (главным образом растительного происхождения), служившие как для облегчения болей, так и для заживления ран. Наряду с этим у Гомера (главным образом в «Одиссее») имеются места, свидетельствующие о наличии в ранней греческой медицине элементов первобытной магии, а также о ее связях с египетской медициной. Отметим, что термин «фюсис», рассмотренный в начале этой главы, впервые встречается также у Гомера («Одиссея», X, 103), причем, по всей видимости, он уже в то время имел отношение к медицинской терминологии...
В VI—V вв. до н. э. В Греции существовало несколько медицинских школ, пользовавшихся известностью. Представителем кротонской (италийской) школы был придворный врач персидского царя Демокед упоминаемый Геродотом; к ней же принадлежал и Алкмеон, о котором будет сказано ниже. Основателем сицилийской школы считался философ Эмпедокл; для нее была характерна тесная связь с религиозно-этнической доктриной пифагорийцев. Знаменитая книдская школа продолжала эмпирические египетских и вавилонских врачей детально описывая отдельные комплексы болезненных симптомов и для каждой болезни разрабатывая свою терапию, включавшую сложные рецепты, диетические предписания и широкое применение местных средств, на пример прижиганий. Сочинения врачей книдской школы до нас не дошли, но их отдельные фрагменты, по-видимому, вошли в состав некоторых трактатов свода Гиппократа. В источниках упоминаются также родосская и киренская школы, но о них мы практически ничего не знаем.
Особое место в истории ранней греческой науки занимает кротонский врач и философ Алкмеон (конец VI — начало V вв. до н. э.). Он был близок к пифагорейцам и развивал взгляды, лежавшие в русле физико-космологической традиции науки «о природе». Однако его значение состоит в другом, а именно в том, что он может в какой-то степени считаться предшественником экспериментальной физиологии и анатомии. По имеющимся сведениям, именно он был первым, кто начал практиковать вскрытие трупов животных в целях изучения строения в функций отдельных органов. Признав мозг важнейшим органом и местопребыванием души, Алкмеон дал исторически наиболее раннее учение об ощущениях, дошедшее до нас в изложении Феофраста. Ему приписывается также открытие нервов, ведущих от органов чувств к головному мозгу.
Большое влияние на медицинские концепции последующего времени оказало учение Алкмеона о здоровье, в основе которого лежала идея равновесия противоположных «сил» — теплого и холодного, сухого и влажного, сладкого и горького и т. д. Заболевание организма, по мнению Алкмеона, вызывается нарушением этого равновесия.
Наибольшую славу уже в древности приобрела косская медицинская школа, неразрывно связанная с именем Гиппократа, уроженца острова Кос, жившего во второй половине V в. до н. э. Гиппократу приписывалось свыше 70 медицинских книг, в своей совокупности составивших так называемый «Свод Гиппократа» («Corpus Hippocraticum»). Книги эти крайне разнородны, и ныне считают, что сам Гиппократ мог быть автором лишь некоторых из них, остальные же написаны в разное время его учениками и последователями. В целом Свод дает весьма полную картину, медицинской теории и практики рассматриваемой эпохи.
Основная черта гиппократовой медицины — строгий рационализм, выступающий здесь в качестве сознательно проводимой тенденции. В этой связи очень характерно сочинение «О священной болезни», в котором опровергается традиционное мнение об эпилепсии как особой болезни, имеющей божественное происхождение. По мнению автора этого трактата, все болезни — и эпилепсия в этом отношении не представляет исключения — вызываются естественными причинами, которые необходимо выяснить и исследовать, чтобы выработать правильные и эффективные методы лечения. В трактате содержится резкая полемика с теми, кто пользуется для излечения болезней заклинаниями и методами религиозно-мистического очищения. По мнению большинства исследователей, эта полемика направлена в первую очередь против врачей сицилийской школы, о которой было упомянуто выше.
Вторая особенность гиппократовой медицины состоит в требовании индивидуального подхода в каждом конкретном случае, определяемого особенностями как самого пациента, так и той естественной среды, в которой он находится. При этом гиппократики широко пользовались понятием «природы» (фюсис), которое у них приобретает поистине универсальное значение. Прежде всего в применении к пациенту «природа» означает совокупность особенностей его телесной и духовной конституции, обусловленных происхождением, наследственностью и действием окружающей среды. Чтобы вылечить больного, врач должен уяснить его «природу» и применить такие методы лечения и такие лекарства, которые не противоречат этой «природе», а согласуются с нею. При этом нужно учитывать «природу» не только организма в целом, но и отдельных его органов. Далее, у каждой болезни также есть своя «природа», которую врач должен знать, чтобы умело направить течение недуга в благоприятную для пациента сторону. Наконец, необходимо использовать «природу» естественной среды, в которой находится больной: особенности климата, характер ветров, свойства воды и т. д. В трактате «О воздухах, водах и местностях», считающимся одной из самых ранних книг Гиппократова свода, излагается влияние этих естественных факторов на «природу» местных жителей и на характер болезней, которым те подвержены. Основной совет, который дается в этой книге странствующему врачу (а таким был, по-видимому, и сам Гиппократ),— по прибытии на новое место первым делом изучить именно эти естественные факторы, чтобы знать их вредное влияние и уметь использовать их целительную силу.
Понятно, что в эпоху Гиппократа медицина еще не имела под собой твердой основы - научной физиологии. Представления гиппократиков о функционировании человеческого организма были весьма наивными и путанными. В то же время в отдельных книгах Свода обнаруживается тенденция нащупать более надежный фундамент, на который могла бы опереться врачебная практика. Так, автор трактата «О древней медицине» возражает против вторжения в медицину современных ему философских концепций (например, учения о четырех элементах Эмпедокла), противопоставляя им гуморальную патологию, которой будто бы придерживались древние врачи и которая объясняет заболевания нарушением равновесного состояния между «соками» (chymoi), определяющими жизнедеятельность организма. Однако по поводу числа и характера этих соков у гиппократиков не было единого мнения: в одних книгах такими соками признаются слизь в желчь, в других — кровь, слизь, вода и желчь, в третьих — кровь, слизь, желтая и черная желчь (точка зрения, которая в дальнейшем стала господствующей и легла в основу учения о четырех темпераментах). Наконец, в трактате «О ветрах» в качестве основного агента, определяющего состояние организма, называется пневма (т. е. воздух). В целом же для гиппократовой медицины характерно отрицание беспочвенного теоретизирования и выдвижение на первый план эмпирических методов исследования, основанных на наблюдении и опыте. И это — третья важнейшая особенность гиппократовой медицины, оказавшаяся особенно плодотворной для развития методов научного естествознания.
Описание конкретных клинических случаев, приводимое в некоторых трактатах Свода, поражает своей точностью и объективностью. В качестве примера приведем два описания, содержащиеся в III книге «Эпидемий» (каждое из них заканчивается лаконичным диагнозом):
«Женщина, жившая у Аристиона, была поражена ангиной. У нее она началась с языка; голос нечистый; язык красный, высыхал. 1-й день — мелкая дрожь, сопровождаемая жаром; на 3-й день — озноб, острая лихорадка; опухоль твердая и красного цвета распространилась на шею и на грудь с двух сторон; конечности холодные, сине-багровые; дыханье поверхностное; питье выливалось через ноздри; больная не могла глотать; стул и моча прекратились. На 4-й день все обострялось; на 5-й день она умерла. Ангина».
«Молодой человек, который жил на площади Лжецов, был охвачен сильной лихорадкой после усталости, тяжелого труда и непривычного бега. 1-й день: расстроенный желудок; выделения желчные, тонкие, обильные; моча тонкая, черноватая; не спал; жажда. На 2-й день все обострилось: стул более обильный, несвоевременный; совсем не спал; расстройство сознания; небольшой пот. На 3-й день тягостное состояние; жажда, тошнота; сильное беспокойство, тоска; галлюцинировал; конечности синие и холодные; напряжение подреберий с двух сторон, без большого вздутия. На 4-й день совсем нет сна; состояние больного ухудшилось. На 7-й день умер; ему было около двадцати лет. Острое заболевание».
Ничего подобного этим описаниям мы не находим в европейской медицинской литературе вплоть до XVI в. Каждое описание — сухой, бесстрастный перечень симптомов; лишь в редких случаях сообщается предписанное лечение. Характерно, что из 42 случаев, описанных в двух книгах «Эпидемий», 25 (т. е. около 60%) окончились смертью; таким образом, автор отнюдь не ставит целью рекламировать свое искусство.
В других книгах Свода сообщаются детальные лечебные предписания. В этом отношении интересен трактат «О внутренних страданиях» (написанный, как считают, под большим влиянием книдской медицинской школы). Каждая глава трактата содержит краткое описание причин и симптомов данной болезни, после чего следуют указания по ее лечению. Подробно описываются рекомендуемые лекарства, включая способы их приготовления и дозировки; даются предписания по доводу диеты и режима больного; в конце указывается прогноз.
Но особой славой как в древности, так и в Новое время пользовался трактат «О переломах», приписываемый большинством исследователей самому Гиппократу. Как и в других трактатах Свода, автор полемизирует против невежества и шарлатанства многих современных ему лекарей, а затем рассматривает различные виды костных переломов и вывихов, в каждом случае, приводя детальное описание приемов лечения. В изложении чувствуется громадный личный опыт автора. Теоретические спекуляции в этом трактате полностью отсутствуют.
Изучение отдельных сочинений Свода Гиппократа показывает, что анатомические знания в Греции поднялись к этому времени на более высокий уровень по сравнению со странами Древнего Востока или с эпохой Гомера. Особенно хорошо был изучен скелет. Основные внутренние органы также были известны, хотя о детальном их строении знали мало, что объясняется существовавшим в Древней Греции запрещением вскрывать трупы умерших. В отношении функций мозга в различных книгах Свода высказываются противоречивые мнения. В одних случаях мозг рассматривается как железа, освобождающая организм от излишней жидкости, в других как орган, вырабатывающий семя, и только в одном из трактатов («О священной болезни») содержится догадка о связи с мозгом не только мышления, ощущений, эмоций, сновидений (эта мысль высказывалась еще Алкмеоном Кротонским), но и психических заболеваний.
Об эмбриологических представлениях гиппократиков мы внаем по книге «О семени и природе ребенка». Принципиальные положения, выдвигаемые автором, не подымаются выше того, что писали по этому поводу досократики, в частности Демокрит: семя происходит из всех частей как отцовского, так и материнского тела; от «силы» и количественного преобладания мужского или женского семени зависит, будет ли ребенок мальчиком или девочкой, а также, на кого из родителей он будет больше похож. Наряду с этим в трактате содержатся интересные наблюдения над развитием раннего человеческого зародыша и проводятся аналогии между развитием человека, с одной стороны, растений и животных (цыпленка) — с другой.
В заключение укажем, что Гиппократу приписывается формулировка основных положений врачебной этики. Так называемая. «Клятва Гиппократа» в большей своей части. сохраняет значение и в наше время.
Математика V — начале IV до н. э. К моменту зарождения науки «о природе» греки, несомненно, уже обладали определенным запасом математических знании, в значительной мере заимствованных у египтян и вавилонян. Но эти знания имели чисто прикладной характер, были случайны, разрознены и потому не составляли науки. Они имели скорее ремесленный характер, ибо сводились к искусству счета, к умению более или менее точно определять площади, находить объемы и, может быть, решать еще какие-то задачи, с которыми грекам доводилось встречаться в их практической деятельности.
Согласно преданию, дошедшему до ученика Аристотеля Евдема, Фалес был первым, проявившим теоретический интерес к некоторым простейшим геометрическим соотношениям. Но даже если это было и так, Фалес, по-видимому, не имел в этом деле прямых продолжателей: ни о ком из последующих мыслителей-ионийцев не сообщается, что они сколько-нибудь серьезно занимались математикой. Следует поэтому согласиться с мнением древних авторов, утверждавших, что заслуга создания математики как теоретической дедуктивной дисциплины принадлежит в основном пифагорейской школе.
Разумеется, это произошло не сразу и не было делом одного лишь Пифагора, как бы он ни был гениален. На ранних этапах существования пифагорейской школы интерес к числу носил религиозно-мистическую окраску. Числам — особенно числам, находившимся в пределах первой десятки,— приписывались особые, сверхъестественные свойства. Эти числа были не просто числа: они составляли сущность окружающего мира, ибо все многообразие вещей и явлений сводилось в конечном счете к числовым соотношениям. Такое отношение к числу было чревато последствиями колоссальной важности. Числа, ранее принадлежавшие к сфере ремесла и практической деятельности, приобрели у пифагорейцев высший онтологический статус. Пифагорейцы начали изучать числа не потому, что это было им нужно для чего-то другого, а потому, что ничего более достойного изучения они не знали.

Рис. 2. Схемы получения рядов треугольных, квадратных и пятиугольных чисел
Отсутствие письменных документов не позволяет сколько-нибудь надежно восстановить последовательность открытий, которые делались в пифагорейской школе. Прежде всего они ввели противопоставления: единица — множество и чет—нечет. Разделению чисел на четные и нечетные придавалось у них особое значение. В связи с этим была тщательно изучена проблема делимости на два (соответствующая теория была воспроизведена Евклидом в IX книге «Начал»). Затем было обращено внимание на то, что некоторые числа (простые) делятся только на самих себя, другие же могут быть представлены в виде произведения двух или большего числа сомножителей. Простые числа пифагорейцы называли «линейными», числа, являвшиеся произведениями двух или трех простых сомножителей, соответственно с — «плоскими» или «телесными».
Далее из натурального ряда были выделены ряды из «треугольных», «квадратных», «пятиугольных» и т. д. чисел. Смысл этих обозначений становится ясным из рис. 2. на котором приведены геометрические построения, дающие получать соответствующие ряды.
Путем аналогичных пространственных построений пифагорейцы получали также «пирамидальные» и т. п. числа.
Дальнейшая разработка делимости целых чисел привела пифагорейцев к идее рациональной дроби. В V в. до н. э. греки научились оперировать, с дробями типа m/n, производя с ними все четыре действия,— с тем ограничением, что вычитать можно было лишь из большего меньшее число (заметим, что египтяне умели производить действия с дробями, но только выражая их в виде дробей типа 1/n). Историки математики предполагают, что к концу V в. до н. э. в Греции уже была построена общая теория делимости, содержавшая в качестве частного случая теорию делимости на 2. Позднее эта теория вошла в состав VII книги Евклида.
Параллельно с арифметикой развивалась также геометрия. Но здесь информация, которой мы располагаем, носит еще более скудный характер. Пифагорейцев прежде всего привлекали свойства фигур (треугольников, квадратов и т. д.), которые могут быть выражены числовыми отношениями. Нетрудно понять, что особый, интерес у них вызвало соотношение между сторонами прямоугольного треугольника, получившее наименование - теоремы Пифагора. Правда, мы не знаем, каким образом и когда было получено доказательство этой теоремы; то доказательство, которое приводится в «Началах» Евклида несомненно имеет более позднее происхождение.
Примерно около середины V в. до н. э. было обнаружено существование несоизмеримых отрезков, т. е. таких, отношение которых друг к другу не может быть выражено не только целым числом, но и любым отношением целых чисел. К их числу принадлежат, например, сторона квадрата и его диагональ. Имеются основания предполагать, что автором открытия был пифагореец Гиппас из Метапонта; с его именем связаны легенды, на которых мы не будем останавливаться. Мы не знаем, каким путем Гиппас пришел к своему открытию; по этому поводу исследователями античной математики выдвигались различные гипотезы.
Открытие несоизмеримости явилось поворотным пунктом в истории греческой математики; по своему значению для того времени оно может быть сопоставлено с открытием неевклидовых геометрий в XIX в. Оно означало крах ранних пифагорейских представлений о том, что соотношения любых величин могут быть выражены через отношения целых чисел. О том резонансе, который вызвало это открытие в образованных кругах греческого общества, свидетельствует ряд мест в сочинениях Платона и Аристотеля, где обсуждаются вопросы несоизмеримости. Вслед за простейшими случаями несоизмеримостей начали изучаться более сложные. Пифагореец Феодор из Кирены (вторая половина V в. до н. э.) показал, что стороны квадратов с площадями 3, 5, 6, 7,..., 17 несоизмеримы со стороной единичного квадрата. А ученик Феодора Теэтет, бывший современником и другом Платона, дал первое общее учение об иррациональных величинах (невыразимых как говорили греки).• Прежде всего он показал, что если площадь квадрата выражается целым числом Ν, которое не является второй степенью другого целого числа, то его сторона всегда будет несоизмерима со стороной единичного квадрата. Далее Теэтет распространил доказательство иррациональности на числа типа 3√N(где N не есть третья степень другого целого числа) √N+√M и M+√N (так называемые «биноминали»), √N-√M и √N-M («апотомы») и √√N√M («медиаль»). Изложение результатов Теэтета содержится в X книге «Начал» Евклида.
Обнаружение несоизмеримых отрезков и тем самым открытие иррациональных («невыразимых») величин поставило греческих математиков перед проблемой первостепенной важности. Каков мог быть выход из трудного положения, в котором оказалась математика в результате этого открытия? Одним из возможных был путь, по которому пошла математика Нового времени,— путь обобщения понятия числа и включения в него более широкого класса математических величин — как рациональных, так и иррациональных. При этом греки могли бы начать разработку чисто аналитических методов решения математических задач. Но они к этому еще не были подготовлены (заметим, кстати, что в греческой математике того времени отсутствовало как понятие нуля, так и понятие отрицательных величин). Поэтому греки избрали другой путь — путь геометризации математики. В результате возникла геометрическая алгебра, позволявшая на основе использования наглядных геометрических образов решать чисто алгебраические задачи; о ее характере мы можем судить по II книге Евклида и по произведениям Архимеда и Аполлония. Эта дисциплина, бывшая типичным детищем эллинского духа, начала закладываться во второй половине V в. до н. э.; она основывалась на античной планиметрии, представлявшей собой геометрию циркуля и линейки, и была приспособлена для решения квадратных уравнений и некоторых других классов алгебраических задач. Но ее возможности были ограничены, и в дальнейшем греческая геометрическая алгебра оказалась тормозом, препятствовавшим свободному развитию математической мысли в древности.
В процессе создания геометрической алгебры греческие математики разработали теорию пропорций, - приспособив ее для оперирования с несоизмеримыми отрезками. При этом было сформулировано новое определение пропорциональности, которое оказалось в равной степени применимым как для рациональных, так и для иррациональных величин. Теорией пропорций занимались Гиппас Meтапонтский, Гиппократ Хиосский, Архит Тарентский и другие математики V и начала IV вв. до н. э. Свое завершение теория пропорций нашла в общей теории отношений, разработанной величайшим математиком IV вв. до н. э. Евдоксом Книдским, о котором речь в следующей главе.
Что касается чистой геометрии, то к началу IV в. до н. э. было в основном завершено, логическое построение планиметрии, включавшей в себя теорию параллельных, определение сумм углов треугольника и площадей многоугольников, теорему Пифагора, теорию, дуг и хорд в круге построения правильных многоугольников и вычисление площади круга. Первое систематическое изложение геометрии было дано Гиппократом Хиосским. Из достижений самого Гиппократа широкую известность получила так называемая «теорема о луночках», изложение которой можно найти в любом курсе истории математики.
Наряду с планиметрией в V и до н. э. начала развиваться и стереометрия. Если ранним пифагорейцам были известны только три правильных многогранника — тетраэдр, куб и додекаэдр, то в дальнейшем к ним прибавились еще два — октаэдр и икосаэдр. А в IV в. до н. э. Теэтет уже дал общую теорию правильных многогранников. Выше уже было сказано о том, что Демокриту приписывалось открытие формул для объемов конуса и пирамиды. Следует также отметить, что в связи с развитием театральной техники возникла потребность в разработке теории перспективы. Автором первого сочинения (может быть, просто инструкции?) по этому вопросу источники называют художника Агафарха, вслед за которым о теории перспективы будто бы писали Анаксагор и Демокрит.
Большую популярность в V в. до н. э. приобрели три геометрические задачи, которые оказались неразрешимы средствами геометрии циркуля и линейки: 1) удвоение куба; 2) трисекция угла; 3) квадратура круга. Задачей об удвоение куба, получившей наименование «делосской задачи», занимались крупнейшие математики того времени — Гиппократ Хиосский и Архит Тарептский; в дальнейшем она явилась толчком к изучению конических сечений. Для решения задачи трисекции угла известный философ-софист Гиппий из Элиды изобрел кривую, впоследствии названную «квадратрисой». Третья задача — квадратура крута — была настолько популярна, что упоминание о ней содержится даже в «Птицах» Аристофана. По преданию, ею занимался в афинской тюрьме Анаксагор. Особый интерес в связи с этой задачей представляют рассуждения софиста Антифона, трактовавшего круг как многоугольник с очень большим числом сторон.
Подводя итоги развитию математики в рассматриваемый• период, мы не можем не поражаться тому гигантскому скачку, который был сделан этой наукой за какие-нибудь полтора столетия. В конце VI в. до н. э. основные математические понятия еще оставались объектом эзотерических спекуляций в пифагорейской школе, а о том, велись ли какие-либо исследования по математике, вне рамок этой школы, мы не имеем никаких сведений. К началу IV в. до н. э. превращается строгую и самостоятельную дисциплину; отвечающую всем критериям подлинной научности. При этом следует подчеркнуть два обстоятельства, сопутствовавших этому прогрессу.
Первое. Примерно в середине V в. до н. э. занятия математикой перестают быть прерогативой одних лишь пифагорейцев, становясь предметом профессиональной деятельности ученых, не примыкавших ни к какому философскому направлению. Бели Феодора из Кирены и Архита из Тарента еще называют пифагорейцами, то Гиппократ Хиосский был, по-видимому, уже чистым математиком-профессионалом. С другой стороны, теоретическая математика начинает привлекать внимание философов, не имеющих отношения к пифагорейской школе; об этом говорят сообщения о занятиях математикой Анаксагора, Гиппия, Антифона и о математических сочинениях Демокрита. Математика становится особой, выделенной наукой, наукой по преимуществу, и в качестве таковой она вскоре начнет рассматриваться как образец для всех прочих наук.
Вторым колоссальной важности обстоятельством следует считать создание дедуктивного математического метода. У нас нет возможности проследить историю возникновения этого метода. Был ли он выработан еще ранними пифагорейцами? Или, как считают некоторые, его рождение было стимулировано логическими рассуждениями Зенона? Или же, наконец, он оформился лишь в процессе творческой деятельности великих математиков конца V в. до н. э.— Гиппократа и Архита? Мы не знаем; нам известно только то, что в книге Гиппократа по геометрии весь материал излагался уже строго дедуктивно — путем логического вывода следствий из небольшого числа исходных положений. Таким образом, мы не сделаем, по-видимому, большой ошибки, приурочив рождение математической науки к моменту появления этой книги.
Астрономия, В отличие от математики греческая астрономия V в. до н. э. не может похвалиться столь же большими, успехами. Прежде всего обращает внимание скудость астрономических знаний у большинства философов-досократиков (вплоть до Демокрита). Их космологические спекуляции не обосновывались ни наблюдениями, ни расчетами; о планетах у них были еще очень смутные представления; даже объяснение солнечных и лунных затмений, данное Анаксагором, было лишь гениальной догадкой, не вытекавшей из космологических концепций самого клазоменца.
И здесь, согласно античным источникам, основные достижения принадлежат пифагорейской школе. Имеются основания предполагать, что гипотеза о шарообразности Земли была сформулирована впервые пифагорейцами (и уже от них заимствована Парменидом). Возможно, не без восточных влияний пифагорейцы научились различать пять планет, и начали наблюдать за их перемещениями. Имеется сообщение, что Алкмеон, который по своим научным воззрениям был близок к пифагорейцам, говорил о движении планет с запада на восток, противоположном движению неподвижных звезд. В дальнейшем в пифагорейской школе оформилась классическая модель космоса, в которой небесные светила располагались на семи кругах, или сферах, в следующем порядке (по мере удаления от Земли): Луна. Солнце. Меркурий. Венера Марс, Юпитер и Сатурн*. Расстояния между этими сферами уподоблялись пифагорейцами интервалам музыкальной гаммы, причем они предполагали, что при своем вращении сферы издают соответствующие тона, в совокупности образующие «небесную» гармонию, или музыку сфер, которая не воспринимается нами, потому что наши уши к ней привыкли.
О космологической системе пифагорейцев в том виде, в каком она сложилась к первой половине IV в. до н. э., можно составить представление по «Тимею» Платона. Однако к модели космоса, изложенной в «Тимее», пифагорейская наука пришла, по-видимому, не прямым путем. Наиболее интересное уклонение представляла собой система Филолая из Тарента — пифагорейца, жившего в конце V в. до н. э. Филолай отказался от традиционного представления о центральном положении Земли и поместил в центр мира огненный «очаг» (Гестию), вокруг которого движутся в порядке удаления от него — невидимая для нас «Противоземля», затем Земля, Луна, Солнце, пять планет и внешняя звездная сфера (рис. 3). Солнце, по Филолаю есть прозрачный шар, заимствующий свои свет и тепло, во-первых, от центрального «очага», а во-вторых, от огня, расположенного за пределами внешней сферы. Введение Противоземли было нужно Филолаю предположительно для того, чтобы сделать число небесных кругов равным десяти. Возможно, впрочем, что у него были и другие соображения, тем более что некоторые досократики (Анаксимен, Анаксагор) также допускали существование невидимых (темных) небесных тел, находящихся ниже Луны.
В источниках сообщаются имена и других ученых той эпохи, которые, не будучи философами, занимались астрономией. Первым из них называют Клеострата Тенедосского, жившего во второй половине VI в. до н. э. и который будто бы оборудовал наблюдательный пункт на горе Иде, откуда следил за движениями небесных светил. Он, вероятно, имел какие-то контакты с вавилонскими астрономами; в частности, ему приписывают установление наименований созвездий зодиака, хорошо известных вавилонянам. Клеострат написал поэму в стихах, называвшуюся «Астрология», от которой до нас дошел один коротенький фрагмент.
Деятельность греческих астрономов в VI—V вв. по н, а. в значительной степени имела практическую направленность, ее важной задачей было уточнение календаря, частности согласование лунного календаря (с которым было связано большинство религиозных ритуалов) с фактической длительностью солнечного года. Эта задача решалась путем установления многолетних циклов, между которыми требовалось вставлять дополнительные месяцы. В качестве первого такого цикла называют «октаэтериду» («восьмилетие»), введенную то ли Клеостратом, то ли его учеником Гарпалом; последнему приписывается также уточнение длительности солнечного года. Между прочим, имеется любопытное указание, что Гарпал был именно тем греком, который помог Ксерксу навести мосты через Геллеспонт.
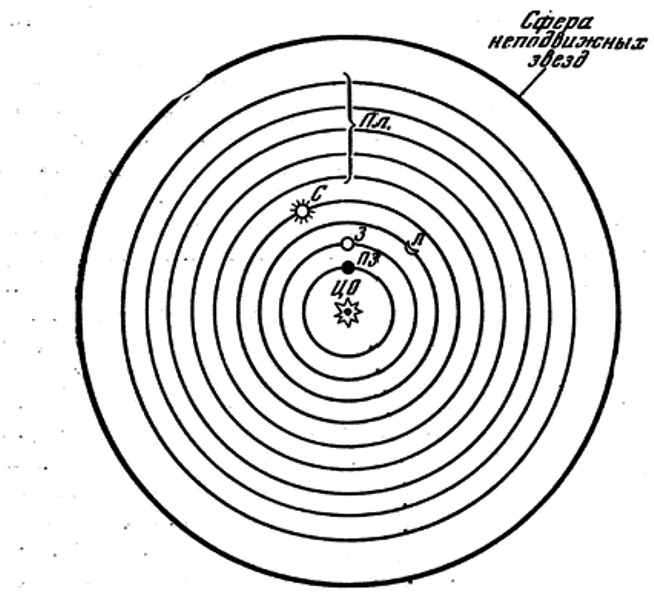
Рис. 3. Система мира по Филолаю:
ЦО — центральный огонь, ПЗ — противоземля, 3 — Земля, Л — Луна, С — Солнце, Пл — пять планет (последовательность которых источниками не засвидетельствована)
Более определенные сведения имеются о двух афинских астрономах второй половины V в. до н. э,— Метоне и Евктемоне. Свои наблюдения они проводили в разных местах — в Афинах, на Кикладах, в Македонии и Фракии. Оба они упоминаются в связи с полным солнечным затмением, имевшим место 27 июня 432 г. до н. э. Метой (кстати сказать, осмеянный Аристофаном в «Птицах») установил 19-ти летний лунно-солнечный цикл, состоявший из 235 месяцев, семь из которых были дополнительными; 110 месяцев этого цикла имели до 29 дней, 125 — по 30 дней. Солнечный год, по Метону содержал 365 5/19 (365,263) дней, что всего лишь на полчаса отличается от точного значения. Что касается Евктемоиа, то ему и присваивается обнаружение неодинаковой длительности времен года; согласно его наблюдениям, астрономические времена года равны соответственно 90, 90, 92 и 93 дням.
Примерно в гаже время жил Энопид Хиосский, который, как считают, был первым астрономом, измерившим наклон эклиптики по отношению к экватору. Он также предложил свой лунно-солнечный цикл, который равнялся 59 годам. Длительность солнечного года Энопид оценил в 365 22/59 дней.
Из всего сказанного явствует, что по сравнению с бурным взлетом математики достижения греческих астрономов в рассматриваемый период были более чем скромными. И все же было бы несправедливо недооценивать значение кропотливой работы, проводившейся такими людьми, как Энопид, Метон и Евктемон. Эта работа подготавливала фундамент, на котором впоследствии было воздвигнуто здание античной теоретической астрономии Евдокса—Гиппарха—Птолемея.
*В пифагорейской школе эти планеты имели, конечно, другие наименования.
|
