§ 71. Развитие интерпретации квантовой механики

Как было отмечено выше, математический аппарат квантоЕой механики был создан очень быстро. Однако он в значительней степени был разработан путем догадок, проведенных весьма нестрогих с логической точки зрения аналогий и т. д. И хотя этот аппарат весьма успешно применялся и позволял решать многие задачи атомной физики, тем не менее физический смысл ноеой теории казался неясным и противоречивым.

Матричный вариант квантовой механики вообще создавался при принципиальном отказе от использования какой-либо картины физических процессов, происходящих в атоме, и с самого начала имел чисто формальный характер; что же касается волнового варианта квантовой механики, то хотя де Бройль, а затем Шредингер и пытались опираться на некоторые конкретные физические представления, тем не менее эти представления были не вполне ясными и также противоречивыми. Представление Шредингера о частице как о волновом пакете было быстро подвергнуто существенной критике. Его же идея о том, что волновая функция представляет собой размазанный заряд электрона, также встречала серьезные возражения и не разделялась ни Бором, ни Гейзенбергом, ни другими физиками-теоретиками, работающими в области теории атома.

Решающий шаг на пути выяснения физического смысла квантовой теории был сделан Борном, который, как мы видели выше, указал на статистический смысл волновой функции. Эта точка зрения Борна скоро стала общепризнанной. Однако выяснение статистического характера волновой функции еще далеко не решало всех методологических вопросов квантовой механики. Оставались вопросы о смысле статистичности квантовой механики, проблема так называемого корпускулярно-волнового дуализма микрочастиц и т. д. Все эти вопросы стояли перед физиками, работающими в области теории атома, а также философами, которые занимались методологическими проблемами физики. В самом начале возникло два основных направления в интерпретации квантовой механики.Одно из них заключалось в попытке мыслить как реально существующие и частицы, и некие реальные волны, т. е. решить проблему корпускулярно-волнового дуализма как сосуществование и частицы, и волны. На этот путь первоначально встал де Бройль, однако он не смог получить положительных результатов.

Второе направление в интерпретации квантовой механики, возглавляемое Бором, Гейзенбергом и др., известно как интерпретация копенгагенской школы. Эта интерпретация получила довольно широкое распространение.

Остановимся сначала на интерпретации квантовой механики, которую пытался дать де Бройль в 1927 г.¹. Собственно говоря, де Бройль предположил сразу две интерпретации квантовой механики. Одной из них была теория двойного решения. Смысл ее заключался в следующем. Де Бройль рассматривал свободную частицу и в качестве волнового уравнения предлагал взять уравнение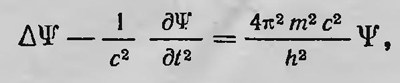

которое является в отличие от уравнения Шредингера релятивистски инвариантным². В качестве решения этого уравнения можно взять плоскую синусондальную волну, которая распространяется, например, в направлении оси z с амплитудой, зависящей и от х, у, z, и от t:

Ψ'=f (х, у, z, t) cos 2πν (t — vz/c² + φ₀).

При этом f(x, у, z, i) — функция, удовлетворяющая уравнению

Δf= 1/c² δ²f/δt².

В частности, f(x, у, z, t) может быть функцией, которая имеет особую точку (сингулярность), которая перемещается с постоянной скоростью ѵ вдоль оси z. Например, можно положить, что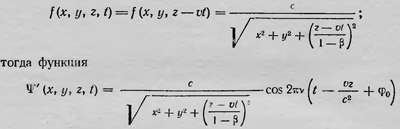

описывает синусоидальную волну, распространяющуюся вдоль оси z со скоростью с²/ѵ, имеющую сингулярность в точке х = у = 0 и z = vt, которая, в свою очередь, движется вдоль оси z со скоростью ѵ. Сингулярность, по мнению де Бройля, и представляет частицу,с которой связана волна Ψ'(x, y, z, t). Эта точка зрения напоминает идею Шредингера о волновом пакете, но она лишена ее недостатков. Де Бройль рассчитывал обобщить ее и на более общий случай, когда частица движется в силовом поле. Кроме того, де Бройль рассчитывал связать это толкование с обычным статистическим толкованием волновой функции. Он предлагает рассмотреть «облако», т. е. совокупность частиц, движущихся с одной и той же скоростью ѵ вдоль оси z. Образуем для этой совокупности функцию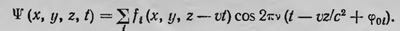

Примем, что все φ_0i равны между собой (например, все φ_0i=0); тогда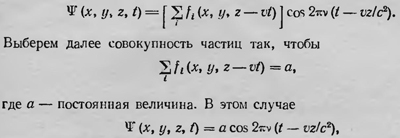

т. e. получена плоская волна, распространяющаяся вдоль оси z с той же скоростью, что и волна, связанная с частицами.

Очевидно, что Ψ(x, y, z, t) — также решение данного волнового уравнения. Но это решение имеет совсем другой смысл, нежели решение с сингулярностью Ψ'(x, y, z, t). Оно определяет уже не одну частицу, а целый ансамбль частиц, и функции Ψ(x, y, z, t) можно придать статистический смысл. Действительно, а² можно рассматривать как плотность частиц в данной точке пространства (в нашем простейшем случае эта плотность постоянна во всем пространстве), а вместе с этим как вероятность обнаружить частицу в этой точке. Таким образом, функция Ψ(x, y, z, t) не что иное, как обычная волновая функция, введенная Шредингером.

Полученный результат и выводы из него де Бройль пытался обобщить на случай нахождения частицы в силовом поле.Он предположил что и в общем случае волновое уравнение должно иметь два решения. Причем одно из них

Ψ'=f(x, y, z, t)cos 2π/h φ

имеет подвижную сингулярность и представляет одну частицу и соответствующая волна имеет определенный реальный физический смысл. Второе решение

Ψ(x, y, z, t)=ψ(x, y, z)cos 2π/h φ

определяет обычную волновую функцию, которая имеет вероятностный статистический характер. При этом фазы у Ψ и Ψ' одинаковы Де Бройль не смог провести эту идею. Он встретился с большими математическими трудностями и поэтому, хотя первоначально и рассчитывал с помощью теории двойного решения дать физическое толкование корпускулярно-волнового дуализма, тем не менее отказался на долгое время от разработки этой теории.

В этой же работе, а затем в докладе на пятом Сольвеевском конгрессе в 1927 г. де Бройль изложил несколько иную интерпретацию квантовой механики, названную им теорией «волны-пилота». Теперь он уже не рассматривал частицу как подвижную сингулярность некоего действительного волнового поля, а представлял ее как обычную материальную точку. Но движение этой материальной точки происходило так, что оно как бы управлялось волной Ψ, являющейся решением волнового уравнения. Волновая функция должна быть комплексной и может быть представлена в виде Ψ = Re^{2π/h iφ}, где R и φ — действительные функции координат и времени.

Если перейти к классическому приближению, то функция φ становится функцией действия Гамильтона S. Тогда скорость частицы u = 1/m grad S. Де Бройль полагает, что и в квантовой механике сохраняется аналогичное соотношение, а именно v=1/m gradφ.

Таким образом, если знать волновую функцию частицы для данной квантовомеханической задачи, то можно вычислить и скорость этой частицы в любой момент времени, а зная к тому же ее начальное положение,— определить и ее траекторию. Однако начальные положения частицы неизвестны и из решения уравнения Шредингера можно определить только вероятность нахождения частицы в каком-либо элементе объема dv в любой момент времени, которая равна |Ψ|² dv, т. е. мы будем знать статистический ансамбль материальных частиц и его изменение со временем, и волновая функция Ψ здесь играет уже роль необычного нематериального поля, описывающего плотность частиц в этом статистическом ансамбле. Она как бы управляет движением всего ансамбля и каждой его частицы.

Теория «волны-пилота» подверглась критике, против которой де Бройль не смог найти возражения. В результате этого он также отказался от этой теории. Таким образом, попытка де Бройля интерпретировать квантовую механику, основываясь на представлении о реальности особых волн, особой точкой которых является частица, или на представлении о классической частице, движением которой управляет волна вероятности, оказалась неудачной. Однако такие попытки и со стороны де Бройля, и других физиков возобновились гораздо позже, уже в 50-х годах.

Тем временем вызревала совершенно иная интерпретация квантовой механики, получившая название «копенгагенской». Ее основоположниками были Гейзенберг и Бор. Первоначально при построении квантовой теории в форме матричной механики Гейзенберг вообще отказался от каких-либо наглядных представлений и рассматривал свою теорию как некий вычислительный, чисто формальный аппарат. Однако, познакомившись с работами Шредингера, он пришел к заключению, что в новую теорию все же нужно вложить определенное наглядное физическое содержание. Это он сделал уже в 1927 г. в работе «О наглядном содержании квантовой кинематики и механики»³.

Так же как Эйнштейн при построении теории относительности, анализируя понятия пространства и времени, исходил из операции измерения, так и при интерпретации квантовой механики нужно провести анализ основных понятий механики применительно к микрообъектам, исходя из рассмотрения операции измерения. Так, для того чтобы определить, что следует понимать под словом «координата», нужно указать эксперимент, с помощью которого мы предполагаем ее измерять. «Никакого другого смысла это слово не имеет»⁴, полагает Гейзенберг. То же относится и к другим физическим понятиям и величинам. Они определяются операциями измерения.

Анализируя далее возможности измерения в квантовой механике, Гейзенберг приходит к важному принципиальному результату о невозможности одновременного точного измерения двух канонически сопряженных величин и устанавливает так называемое соотношение неопределенностей

Δq_iΔp_i~h,

где Δq_i — точность определения (измерения) какой-либо из координат частицы, Δp_i — точность одновременного определения (измерения) соответствующего импульса. В дальнейшем Гейзенберг и Бор разобрали ряд примеров мысленных экспериментов по измерению канонически сопряженных величин, координат и импульсов. Во всех случаях получался результат, согласный с принципом неопределенности. Принцип неопределенности, по Гейзенбергу, и служит наглядным выражением «таинственного» правила квантования или выражением перестановочного соотношения матричной формы квантовой механики. Одновременно этот принцип является основой наглядной физической интерпретации квантовой механики.

Бор, размышляя над задачей интерпретации квантовой механики, пришел к более общим идеям, положенным им в основу выдвинутого им принципа дополнительности, который включал в себя и принцип неопределенности Гейзенберга. Этот принцип дополнительности Бор и положил в основу интерпретации квантовой механики. Отправной точкой для Бора являлся установленный факт наличия корпускулярно-волнового дуализма как для света, так и для вещества («материи»). И свет и частицы проявляют в различных условиях противоречивые свойства, и в связи с этим о них возникает противоречивое представление. С одной стороны, они представляются нам в виде непрерывного поля, распределенного в пространстве, будь то световое поле или поле, которое описывается волновой функцией. С другой стороны, и свет и, например, электрон выступают как частицы, как материальные точки Эти два представления, являясь необходимыми, с другой стороны, исключают друг друга. Они, по Бору, являются дополнительными. Далее, при одном представлении микрообъекта используется причинное описание соответствующих процессов, в другом же случае пространственно — временное. В этом и заключается сущность принципа дополнительности.

Принцип дополнительности означает также, что в квантовой механике используется статистическое описание явлений, происходящих в микромире, и что строгое детерминистическое описание элементарных процессов исключается.

Причиной корпускулярно-волнового дуализма, по Бору, является то обстоятельство, что сам микрообъект не является ни волной, ни частицей в обычном понимании. Однако, вследствие того что сведения об этом объекте, о его характеристиках получают в результате его взаимодействия с классическим прибором, т. е. макроскопическим объектом, следует описывать этот микрообъект в классических понятиях, т. е. использовать классические представления о волне и частице. Мы как бы вынуждены говорить на классическом языке, хотя с его помощью нельзя выразить все особенности микрообъекта, который не является классическим. В своей интерпретации Бор затрагивал и общие философские, методологические вопросы, относящиеся к микроявлениям. Во-первых, он выступил за отказ от причинности в элементарных процессах. Во-вторых, он высказал идею о невозможности объективного представления о микрообъекте, о «невозможности приписать самостоятельную реальность в обычном физическом смысле ни явлениям, ни средствам наблюдения»⁵. Свои идеи о интерпретации квантовой механики Бор высказал в докладе на Международном конгрессе физиков в Италии осенью 1927 г. Доклад Бора произвел большое впечатление на участников конгресса, но вызвал и возражения. Особенно резко выступали Шредингер и Лауэ.

«Но почти все присутствующие,— пишет Р. Мур в биографии Бора,— единодушно сошлись на одном — отвергая принцип неопределенности, индетерминизм и статистику, они яростно настаивали на том, что физика должна оставаться на позициях «реальности». Даже самая незначительная часть Вселенной должна существовать так же объективно, как город или камень, независимо от того, доступна она наблюдению исследователя или нет»⁶.

На состоявшемся в том же году пятом Сольвеевском конгрессе развернулась дискуссия вокруг доклада де Бройля, в котором излагалась теория «волны-пилота», и докладов Бора, Борна и Гейзенберга, также посвященных интерпретации квантовой механики — копенгагенской интерпретации. Против копенгагенской интерпретации выступили Лоренц, Эйнштейн и Шредингер. Защищали же ее Бор, Гейзенберг, Дирак и Паули. Прежде всего вопрос коснулся причинности в элементарных процессах. Защитники этой интерпретации утверждали необходимость отказа от причинности в элементарных процессах. Дирак, например, высказывался за признание того, что в единичных микропроцессах «природа делает свободный выбор»⁷. Гейзенберг же, отстаивая точку зрения об недетерминированности атомных процессов, говорил, что «наблюдатель сам делает выбор»⁸. Лоренц категорически возражал против признания индетерминизма в элементарных процессах. Эйнштейн также не соглашался с такой постановкой вопроса. Он говорил, что не может допустить, что в атомных процессах «господь прибегает к помощи игральных костей»⁹.

Эйнштейн был не только противником вывода о том, что в элементарных процессах отсутствует причинность. Он активно выступил на конгрессе против основных положений копенгагенской интерпретации квантовой механики. Между Эйнштейном и Бором развернулась дискуссия по вопросу о понимании квантовомеханических закономерностей. Эйнштейн четко поставил вопрос о смысле интерпретации квантовой механики Бором и другими представителями копегагенской школы. На общей дискуссии он рассмотрел следующий пример. Пусть электроны проходят малое отверстие в экране, за которым в виде полусферы расположена фотопленка, фиксирующая место попадания каждого электрона. Вследствие дифракции каждый электрон может обнаружиться, вообще говоря, в любой точке фотопленки и согласно квантовой механике вероятность попадания определяется квадратом амплитуды волновой функции.

Возможны два различных подхода к рассмотрению данного явления. В первом случае полагаем, что частица в результате пока неизвестных причин, проходя отверстие в экране, отклоняется от прямолинейного пути, движется по какой-то траектории и затем попадает на фотопленку. Такой подход ничем принципиально не отличается от постановки вопроса в классической физике. Он указывает на неполноту квантовой механики в смысле описания поведения единичного микрообъекта и предполагает дальнейшее развитие теории микроявлений в направлении построения теории единичного процесса, основанной на принципе причинности. Эта точка зрения как раз соответствует первоначальным попыткам де Бройля построить причинную теорию микропроцессов, о которой говорилось выше.

Второй подход к пониманию данного эксперимента, характерный для копенгагенской интерпретации, заключается в следующем. Утверждается, что частица, проходя отверстие в экране, не находится в каких-либо определенных точках пространства и может локализоваться на фотопленке в любой точке с вероятностью, равной квадрату амплитуды соответствующей волновой функции ψ. Причем процесс ее локализации происходит мгновенно.

Эйнштейн был не согласен с последней точкой зрения. Он ищет внутренние противоречия в таком представлении. В частности, полагает, что мгновенная локализация частицы в какой-то точке «приводит к противоречию с постулатом относительности»¹⁰. Эйнштейн привел еще ряд соображений против копенгагенской интерпретации. В частности, он поставил вопрос: нельзя ли в указанном выше мысленном эксперименте, используя законы сохранения, получить более точные сведения о состоянии частицы после прохождения отверстия в экране, нежели это позволяет принцип неопределенности? Если это можно сделать, то следовало бы признать, что копенгагенская интерпретация содержит внутренние противоречия. Тогда были бы естественны поиски более общей теории, основанной уже на принципе причинности. Однако анализ этого вопроса привел к убеждению, что принцип неопределенности с необходимостью должен выполняться в данном эксперименте. Таким образом, это возражение Эйнштейна, так же как и другие, было снято. Однако Эйнштейн не признал копенгагенскую интерпретацию истинной. Он был убежден, что статистический характер квантовой механики связан с ее неполнотой, т. е. что эта теория имеет дело с неполным набором величин, необходимых для описания физических систем, и интерпретация Бора не является убедительной.

Пятый Сольвеевский конгресс подвел итог первому этапу развития квантовой механики. В результате дискуссии выкристаллизовались две основных точки зрения на квантовую механику как на теорию микропроцессов. Физики теперь разделились на два основных лагеря. В первом лагере находились Бор, Гейзенберг, Борн, Дирак, Паули и некоторые другие, которые следовали копенгагенской интерпретации и считали, что основой квантовой механики является принцип дополнительности. Они рассматривали квантовую механику как логически непротиворечивую замкнутую и полную теорию микроявлений, в которой описание микроявлений принципиально статистическое.

Вторая точка зрения заключалась в том, что, несмотря на то что квантовая механика — важнейшее достижение физической науки, она должна основываться на другой, более общей теории, которая позволяла бы давать не только статистическое описание элементарных процессов и с помощью которой можно было бы создать непротиворечивый образ микрообъекта. Эта более общая теория могла бы строиться на представлении о так называемых скрытых параметрах, т. е. на представлениях о существовании таких физических величин, относящихся к самим частицам или к каким-то другим, неизвестным пока микрообъектам, действия которых однозначно определяют поведение электрона или другого подобного физического объекта. В той или иной степени последней точки зрения придерживались физики более старшего поколения: Лоренц, Планк, Эйнштейн и другие. Однако, выдвигая различные возражения против копенгагенской интерпретации, они не могли предложить никакой конкретной теории, которую можно было бы противопоставить первой. Возникшая было теория де Бройля, о которой говорилось выше, была подвергнута критике, и он сам от нее отказался. Особенно активно против представлений Бора продолжал выступать Эйнштейн, который и после Сольвеевского конгресса неоднократно возражал против теории дополнительности, старался показать, что квантовая механика не является логически замкнутой, что она содержит внутреннее противоречие. Но прежде чем говорить о последующих возражениях Эйнштейна, нужно упомянуть о философской борьбе, которая развернулась вокруг понимания квантовой механики.

Квантовая механика затрагивала целый ряд общих философских вопросов: вопрос причинности, вопросы теоретико-познавательного характера, такие, как вопрос о возможности познания, о роли субъективного фактора в познании и т. д. Вполне естественно, что все эти вопросы подвергались философскому анализу, часто неразрывно связанному с анализом физического содержания самой теории. Прежде всего острая полемика разгорелась вокруг вопроса причинности в элементарных процессах. Здесь и физики и философы разделились на два противоположных лагеря. Одни из них встали на точку зрения отказа от причинности в элементарных процессах. Другие же продолжали оставаться на позициях детерминизма, надеясь на построение в будущем более общей «детерминистической» теории микроявлений, основанной на представлении о скрытых параметрах.

Второй философской проблемой, возникающей в связи с квантовой механикой, была проблема реальности микрообъектов и роли субъективного фактора в познании микроявлений. Остановимся сначала на втором вопросе (вопрос причинности рассмотрим позже).

Так же как положение об относительности размеров тел и промежутков времени в теории относительности породило идею о субъективном характере этих понятий и было использовано позитивизмом для подтверждения своей философии, так и основные идеи теории дополнительности были использованы для обоснования отказа от признания объективности микрообъектов. Согласно корпускулярно-волновому дуализму и принципу дополнительности свойства микрообъекта, его конкретный образ выступает перед нами всегда вместе с прибором и проявляется в состоянии этого макрообъекта — прибора. При этом вследствие принципа неопределенности этот образ принципиально различен в зависимости от того, какой прибор использует исследователь (наблюдатель). В связи с этим у ряда физиков и философов возникает вопрос: можно ли вообще говорить о существовании микрообъекта самого по себе, в то время когда он не взаимодействует с макрообъектом или с прибором? Ученые и философы, находящиеся в большей или меньшей степени под влиянием позитивизма или какого-либо другого идеалистического направления, начинают более или менее определенно склоняться к отрицательному ответу на этот вопрос, начиная с прямого отрицания объективного существования электрона или другого какого-либо микрообъекта и кончая мнением, что микрообъект сам по себе является чем-то неопределенным, подобно кантовской «вещи в себе». Так, например, Иордан в книге «Наглядная квантовая теория», вышедшей в 1937 г., сводя существо квантовой механики к теории дополнительности, утверждает, что в квантовой механике «то характерное для классического способа описания отделение акта наблюдения от объективного физического носителя вещей не проводимо и представление об объективной картине процессов теряет свою справедливость»¹¹. Иордан считает, что квантовая механика приводит к признанию невозможности разделения наблюдателя и наблюдаемого объекта, т. е. субъекта и объекта. Он прямо указывает, что теоретико-познавательная постановка вопроса в квантовой механике существенно не отличается от таковой в рамках позитивистской философии. В связи с этим он пишет:

«Для меня работы Эрнста Маха представляют не лишнюю основу для понимания новейшего квантово-физического способа описания и родство идей Маха с ним кажется мне гораздо существенней, нежели имеющееся между ними различие»¹².

Несколько иную философскую интерпретацию квантовой механики давал Гейзенберг. Смешивая идеи субъективного и объективного идеализма, он полагал, что квантовая механика ведет в известном смысле к возрождению идей Пифагора и Платона. Подобно атомам Платона, представляющим собой простые геометрические фигуры, атом современной физики также лишен каких-либо качеств и свойств, кроме чисто математических.

«Атом современной физики,— писал Гейзенберг в 1932 г.— может быть лишь символически представлен дифференциальным уравнением в частных производных и в абстрактном многомерном пространстве; только эксперименты наблюдателя вынуждают атом принимать известные положения, цвет и определенное количество теплоты. В современной физике для атома все качества являются производными; непосредственно он не обладает никакими материальными свойствами»¹³.

Более тонкую философскую интерпретацию квантовой механики дал Бор, в частности, в интересной полемике с Эйнштейном, введя так называемое понятие «физической реальности».

Как уже говорилось выше, Эйнштейн начиная с 1927 г. неоднократно выступал против копенгагенской интерпретации квантовой механики, стараясь показать ее неполноту и противоречивость. После пятого Сольвеевского конгресса, на котором имела место первая дискуссия с Бором, Эйнштейн выступает на шестом Сольвеевском конгрессе, состоявшемся в 1930г. Он опять приводит пример мысленного эксперимента, из которого как будто бы следует, что квантовая механика содержит внутренние противоречия. Однако Бор показал, что Эйнштейн не прав. Не имея возможности изложить эту дискуссию между Эйнштейном и Бором, перейдем к следующему выступлению Эйнштейна против копенгагенской интерпретации¹⁴. В 1935 г. Эйнштейн совместно с Подольским и Розеном опубликовал статью «Можно ли считать квантовомеханическое описание физической реальности полным»¹⁵. В статье рассмотрен следующий пример. Представим себе две частицы, которые взаимодействуют в течение некоторого времени и в это время представляют одну систему, так что их общее состояние описывается, например, волновой функцией Ψ(x₁, x₂), где x₁ и x₂ — координаты частиц. После определенного момента времени они разлетаются на большое расстояние и взаимодействие между ними прекращается. Их можно считать независимыми. Однако в результате того, что они представляли во время взаимодействия одну систему, их состояние после прекращения взаимодействия по-прежнему описывается общей функцией Ψ(x₁, x₂).

Пусть теперь a₁, а₂, а₃, ...— собственные значения некоторой величины A, относящейся к первой частице после прекращения взаимодействия, которой соответствует оператор А; u₁(х₁), u₂(x₂), ... — соответствующие собственные функции этого оператора. Тогда функцию Ψ(x₁, x₂), рассматриваемую как функцию от х₁, можно разложить в ряд по собственным функциям оператора А: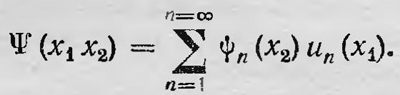

Если теперь измерить величину А у первой частицы, то мы получим одно из значений a₁, а₂, а_3k. Тогда вследствие того, что все u₁(х₁), u₂(x₂), ..., кроме u_k(х_i), равны нулю, получаем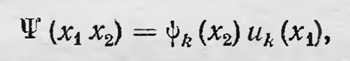

а это означает, что состояние второй частицы описывается функцией ψ_k(x₂). Таким образом, измерив величину А у первой частицы, можно определить волновую функцию, описывающую состояние второй частицы. Можно, однако, поступить иначе. Вместо величины А выберем какую-либо другую величину В, которая характеризуется оператором В и имеет собственные функции v₁(x₁), v₂(x₁), v₃(x₁) ... и соответствующие собственные значения b₁, b₂, b₃, ..., и разложим функцию по собственным функциям оператора В так, что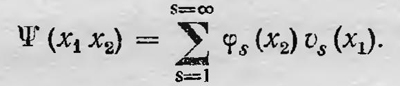

Измерим теперь величину В у первой частицы. Допустим, что получено значение b_r. Очевидно, что это одновременно означает, что вторая частица находится в состоянии, описываемом уже не функцией ψ_k(x₂), а функцией φ_r(x₂).

Таким образом, в результате двух различных измерений, проведенных над первой частицей, вторая частица может оказаться в двух различных состояниях, описываемых разными волновыми функциями, и это несмотря на то, что между ними нет уже никакой реальной связи, никакого взаимодействия. Может оказаться также, что волновые функции ψ_k(x₂) и φ_r(x₂) — функции двух некоммутирующих операторов Р и Q (например, они могут быть операторами координаты и соответствующего импульса второй частицы)¹⁶. Тогда мы приходим к выводу, что, не трогая вторую частицу и производя измерения только над первой, которая уже никак не связана со второй, можно определить значение одной из величин, изображающихся двумя некоммутирующими операторами, например, импульс и координату. Такого рода вывод, по мнению авторов, свидетельствует о неполноте квантовой механики. От полной теории, полагают авторы, нужно требовать следующее:

«... каждый элемент физической реальности должен иметь отражение в физической теории»¹⁷.

Под физической реальностью авторы понимают объективную реальность, существующую объективно и независимо от сознания. Эта реальность отражается в теории в понятиях, которые она использует в виде физических величин, каждой из которой должен соответствовать элемент физической реальности. Критерием того, что данной физической величине соответствует элемент физической реальности, является следующее:

«Если мы можем без какого бы то ни было возмущения системы предсказать с достоверностью (т. е. вероятностью, равной единице) значение некоторой физической величины, то существует элемент физической реальности, соответствующий этой физической величине»¹⁸.

Возвращаясь теперь к разобранному примеру и принимая во внимание критерий реальности, авторы приходят к заключению, что необходимо считать р и q второй частицы элементами физической реальности, поскольку они могут быть определены без какого-либо вмешательства в систему с любой степенью точности. Но, с другой стороны, квантовомеханическое описание данной частицы с помощью волновой функции исключает возможность одновременного существования этих двух величин у второй частицы. В этом авторы статьи во главе с Эйнштейном видят противоречие и приходят к выводу о том, что «квантовомеханическое описание физической реальности посредством волновых функций не является полным»¹⁹. В заключение они высказываются за возможность построения более общей (полной) теории микроявлений. Они пишут:

«Мы думаем, однако, что такая теория возможна»²⁰.

Бор немедленно ответил на критику статьей, имевшей то же название.Он показал, что с логической точки зрения никакого противоречия с теорией, основанной на принципе дополнительности, не возникает. Принцип дополнительности утверждает невозможность одновременного точного измерения координаты и соответствующего импульса. Это общее положение квантовой механики не зависит от конкретных особенностей экспериментальных установок, с помощью которых определяются канонически сопряженные величины. Эти величины можно измерять непосредственно или косвенным образом, как это имеет место в примере, рассмотренном Эйнштейном, Подольским и Розеном. Хотя в данном случае при измерении координаты и импульса у второй частицы она не испытывает никакого материального воздействия, тем не менее меняются условия эксперимента и условия, «определяющие возможные типы предсказаний будущего поведения системы»²¹. Противоречие, о котором говорят Эйнштейн и его соавторы, не является логическим противоречием квантовой механики, основанной на принципе дополнительности. Противоречие возникает, если придерживаться старого понятия реальности физического объекта как чисто объективной, независимой от того, как она наблюдается или проявляется при измерении ее макроприбором. По мнению Бора, квантовая механика требует отказа от такого понимания реальности. Основные понятия квантовой механики, утверждает Бор, влекут за собой «необходимость окончательного отказа от классического идеала причинности и радикальный пересмотр наших взглядов на проблему физической реальности»²². Таким образом, по существу, Бор понимает под реальностью (физической реальностью) не сами материальные объекты, а лишь сведения или, точнее, максимально полные сведения о них, лишь их образ, причем не охватывающий всех сторон этих объектов.

Фок в предисловии к переводу статьи Эйнштейна с соавторами и статьи Бора поясняет основную мысль Бора. Он пишет, что Эйнштейн неправильно толкует понятие «состояния» в квантовой механике. В квантовой механике понятие «состояния» сливается с понятием «сведения о состоянии», получаемые в результате определенного максимально точного опыта». Фок писал:

«Если считать вместе с Эйнштейном, что волновая функция описывает объективное состояние, то, конечно, его результат будет иметь характер парадокса. Ведь невозможно себе представить, чтобы объективное состояние системы (что бы мы под этим ни подразумевали) менялось в результате каких-либо операций, произведенных не над ней, а над другой системой, которая с ней вовсе не взаимодействует...». Но, продолжает Фок: «Все парадоксы исчезают, коль скоро мы откажемся от проводимого Эйнштейном неверного «объективного» толкования волновой функции и примем правильное толкование, т. е. будем считать, что она описывает «состояние в квантовом смысле» или «сведения о состоянии», получаемые в результате определенного максимально точного опыта»²³.

Так Фок толкует рассуждение Бора. Но если это так, то действительно Бор в этом рассуждении отдает дань субъективному идеализму, так как у него нет, по существу, разницы между понятиями «объективное состояние» и «сведения о состоянии». И ни о какой объективной реальности Бор не говорит, ставя, по существу, знак равенства между «объективной реальностью» и «физической реальностью», являющейся «сведением о состоянии». Так, собственно говоря, и была понята в свое время точка зрения Бора²⁴.

Дискуссия между Эйнштейном и Бором не закончилась с опубликованием указанных статей. И Эйнштейн, и Бор остались каждый при своем мнении. В дальнейшем Эйнштейн не раз возвращался к рассмотренному примеру²⁵, защищал положение о неполноте квантовой механики и считал, что признание возможности изменения состояния частицы или квантовой системы вообще без какого-либо материального воздействия на нее равносильно признанию наличия телепатии в физических процессах.

В статье «Физика и реальность»²⁶, последовавшей вскоре после опубликования рассмотренной дискуссии, Эйнштейн расценивал метод квантовой механики, основанный на использовании волновой функции, как метод, позволяющий описывать усредненное поведение большого числа атомных систем, а не метод описания отдельных индивидуальных процессов. В согласии с этим он и оценивал квантовую механику как неполную и считал возможным и даже необходимым создание другой, более общей теории. Позже Эйнштейн подчеркивал, что если считать функцию Чг описывающей статистическую совокупность систем, то указанный выше парадоксальный результат о зависимости состояний пространственно отделенных систем пропадает. Но это означает, что квантовомеханическое описание, по мнению Эйнштейна, не является полным. Он писал:

«Пытаясь рассматривать квантовотеоретическое описание как полное описание отдельных систем, мы приходим к неестественной интерпретации теории. Если принять точку зрения, согласно которой такое описание относится к ансамблю систем, а не к отдельным системам, то необходимость в таких неестественных интерпретациях отпадает... Существует, однако, простая психологическая причина, по которой эту почти очевидную интерпретацию до сих пор не принимали во внимание. Дело в том, что если статистическая квантовая теория не ставит перед собой задачи полного описания отдельной системы (и ее развития во времени), то такое описание, очевидно, приходится искать где-то еще. При этом с самого начала необходимо отдавать себе исный отчет в том, что элементы полного описания не содержатся среди фундаментальных идей статистической квантовой теории... В будущей физике (при условии, если попытки построить полное описание физической системы увенчаются успехом) статистическая квантовая теория будет занимать примерно такое же положение, какое занимает статистическая механика в рамках классической механики. Я твердо убежден, что развитие теоретической физики будет происходить именно так, но путь ее будет долгим и трудным»²⁷.

Против философских выводов из копенгагенской интерпретации квантовой механики, имевших в большей или меньшей степени идеалистический характер: или прямо отрицавших объективное существование микрообъектов, или утверждавших, так сказать, их неполную объективность, выступал, конечно, не один Эйнштейн. В многочисленных статьях и книгах содержались критические замечания по поводу таких выводов. При этом были предложены разнообразные толкования и принципа дополнительности и толкования волновой функции и т. д., не выходившие за рамки квантовой механики. Не имея возможности осветить всю дискуссию по этому вопросу, остановимся лишь на двух подходах к интерпретации квантовой механики, имевших методологический характер.

Одной из таких интерпретаций квантовой механики была интерпретация, основанная на понятии квантовых ансамблей. Теория квантовых ансамблей разрабатывалась первоначально К. В. Никольским²⁸, а затем Д. И. Блохинцевым²⁹. Согласно теории квантовых статистических ансамблей функция Ψ является характеристикой не одной частицы, а сразу большого коллектива невзаимодействующих частиц — квантового ансамбля. В этом отношении она аналогична функции распределения, рассматриваемой в классической статистике.

«... Когда говорят, что частица (или, в общем случае, система) находится в состоянии, характеризуемом волновой функцией Ψ, — пишет Блохинцев,—то следует представлять себе большое число (N>>1) таких частиц (или систем), которые независимо друг от друга находятся в том же состоянии и поэтому могут служить для воспроизведения большого числа тождественных опытов»³⁰.

Однако квантовый статистический ансамбль имеет принципиальное отличие от классического статистического ансамбля. Последний всегда можно разложить на подансамбли без дисперсии величин, характеризующих частицы. Например, можно составить такой ансамбль классических частиц, в котором координаты и импульсы частиц имеют определенное значение. Квантовый ансамбль нельзя разложить на подансамбли, в которых одновременно и координата, например х, и сопряженный импульс р_х имели бы определенное значение. Разложить ансамбль на подансамбль можно только с дисперсией так, что ΔpΔх ~ h, т. е. должно выполняться соотношение неопределенностей. Действие прибора заключается в том, что он разлагает квантовый ансамбль на подансамбли. Разные приборы разлагают ансамбли на подансамбли по разным признакам, причем всегда выполняется соотношение неопределенности. Здесь действие прибора аналогично действию спектрального аппарата в оптике, который разлагает в спектр согласно своему устройству падающее на него световое излучение. Такая интерпретация волновой функции и действия прибора, не изменяя конкретное содержание квантовой механики, исключает ее идеалистическое толкование. Здесь микрообъект существует сам по себе без воздействия на него прибора и тем более без измерения над ним. Его состояние определяется объективной волновой функцией. Действие же прибора заключается в том, что он отбирает из квантового ансамбля соответствующие подансамбли, которые он способен отобрать. С точки зрения теории ансамблей Д. И. Блохинцев разрешает и парадокс Эйнштейна, Подольского, Розена. Производя измерения над первой частицей, мы не воздействуем на вторую, которая уже не связана с первой, а просто отбираем соответствующий подансамбль, характеризующий первую частицу, и тем самым выбираем и соответствующий подансамбль для второй частицы. Первоначально при взаимодействии двух частиц имела место корреляция между ними, поэтому, измеряя, например, р_i у первой частицы, мы разлагаем ансамбль по данному признаку и одновременно выделяем подансамбль для второй частицы. Она оказывается принадлежащей подансамблю, характеризуемому по признаку q_i, с соответствующей волновой функцией.

Иначе интерпретировал квантовую механику Фок. Его интерпретация ближе к первоначальной интерпретации Бора, хотя он и отказался от рассмотрения волновой функции как «сведения о состоянии», полагая, что это вносит идеалистический момент в понимание квантовой механики. Фок полагает, что волновая функция характеризует состояние отдельного микрообъекта. Но эта характеристика является объективной, она определяет потенциальные возможности тех или иных проявлений микрообъекта при измерении в зависимости от того, какой прибор при этом используется. Частица может проявляться именно как частица (как материальная точка) или же как объект, обладающий определенной энергией и импульсом. Что же касается парадокса Эйнштейна, Подольского, Розена, то Фок высказал мысль, что в этом случае следует принять, что для микрообъектов существуют как силовые, так и несиловые взаимодействия, т. е., что хотя частицы после обычного взаимодействия и разлетаются на большое расстояние, взаимодействие между ними не прекращается, поэтому процесс измерения над одной частицей оказывает влияние на вторую частицу, меняя ее состояние, хотя никакого обычного взаимодействия между ними уже нет.

«Ошибка Эйнштейна заключается, по-нашему, именно в том, что Эйнштейн отрицает (объявляет телепатией ..) всякие взаимодействия, кроме силовых. Между тем можно привести из разных областей науки и жизни много разнообразных видов взаимодействия, которые все являются несиловыми». В качестве примера Фок приводит воздействие, испытываемое человеком со стороны коллектива, а также взаимодействие, выражаемое принципом Паули. В заключение он отмечает, что «существование несиловых взаимодействий не подлежит сомнению. Но если их признать, то отпадает и рассмотренная Эйнштейном дилемма..., а с нею падает и парадокс, приводящий его к мнению о неполноте квантовой механики»³¹.

Конечно, трудно себе представить, чтобы между частицами, между которыми имела место обычная силовая связь, существует еще какая-то связь, причем остающаяся при сколь угодно большом расстоянии. Сразу же возникают вопросы: что это за связь? какова ее природа? Правда, спустя два года Фок уже говорит о «логической связи»³². Но логическая связь между двумя частицами, находящимися сколь угодно далеко друг от друга, так же трудно себе представить, как и несиловую связь. Однако развитие современной науки уже приучило нас к самым неожиданным и парадоксальным выводам. Сейчас физики говорят уже и об отрицательных и даже мнимых массах и тому подобных вещах. Возможно, что и в идее несиловой или логической связи имеется рациональное зерно.

Перейдем к рассмотрению развития представления о причинности в элементарных процессах. При этом рассмотрим, как в процессе развития физики вообще развивалось представление об этой важной категории в физике.

¹L.de Broglie. Journ. d. Phys., ser. VI, t. VIII, № 5, 1927, p. 225.
²Это уравнение является частным случаем релятивистского уравнения, полученного помимо де Бройля в общем виде целым рядом физиков в 1926 г. Оно известно как уравнение Клейна—Фока—Гордона. Как выяснилось, данное уравнение пригодно только для частиц с нулевым спином. Релятивистское же уравнение для электрона было установлено Дираком в 1928г.
³Heisenberg W. Zeitschr. f. Phys., В. 43, 1927, S. 172.
⁴Heisenberg W. Zeitschr. f. Phys., В. 43, S. 174.
⁵Бор Н. Избранные научные труды. Т. II. М., «Наука», 1971, с. 31.
⁶Мур Р. Нильс Бор — человек и ученый. М., «Мир», 1969, с. 198.
⁷Electrons et Photons. Rapportset discussion du 5е Conseil de Physique. De l’institut international de physique Solvay. Paris, 1928, p. 262—263.
⁸Там жe, p. 264.
⁹Albert Einstein — Philosopher—Scientist. N. G., 1951, p. 218.
¹⁰Эйнштейн А. Собрание научных трудов. Т. III, с. 530.
¹¹Jоrdаn Р. Anschauliche Quantentheorie. Berlin, 1936, S. 308.
¹² Jordan Р. Anschauliche Quantentheorie, S. 308.
¹³Гейзенберг В. Философские проблемы атомной физики. М., ИЛ, 1953, с. 32
¹⁴Полемика Эйнштейна с Бором на шестом Сольвеевском конгрессе в 1930 г. изложена в статье Бора «Дискуссии с Эйнштейном о проблемах теории познания в атомной физике» (Бор Н. Избранные научные труды Т. П, с. 399).
¹⁵Статья Эйнштейна с соавторами, ответ на нее Бора, а также комментарии к этим статьям Фока помещены в журн. УФН, т. 16, 1936, вып. 4, с. 436.
¹⁶Что такой случай возможен, авторы показывают на конкретном примере.
¹⁷УФН, т. 16, 1936, с. 440. См. также: Эйнштейн А. Собрание научных трудов. Т. 111, с. 605.
¹⁸Там же, с. 440—441.
¹⁹Там же, с. 446.
²⁰Там же, с. 440—441.
²¹УФН, т. 16, 1933, с. 454.
²²Там же, с. 448.
²³Там же, с, 437—438.
²⁴Позиция Фока впоследствии изменилась. Он уже перестал считать волновую функцию простым «сведением о состоянии» (об этом будет сказано ниже).
²⁵Эйнштейн А. Автобиографические заметки. Замечание к статьям и др.— В кн.: Эйнштейн А, Собрание научных трудов. Т. IV.
²⁶Эйнштейн А. Собрание научных трудов. Т. IV, с. 200.
²⁷Там же, с. 300.
²⁸См.: Никольский К. В. Квантовые процессы. М.—Л.. Гостехиздат, 1940.
²⁹См. напр.: Блохинцев Д. И. Основы квантовой механики. М.—Л.» Гостехиздат, 1949 (и последующие издания).
³⁰Там же, с. 54.
³¹УФН, т. 59, 1956, вып. 1, с. 116.
³²УФН, т. 66, 1958, вып. 4, с. 592.

<<Назад Вперёд>>

Просмотров: 4232

загрузка...

Другие книги по данной тематике