§ 66. Создание общей теории относительности

После того как Эйнштейн установил основные положения специальной теории относительности, он начал задумываться над обобщением этой теории, а именно над распространением принципа относительности на случай неинерциальных систем. Такую возможность он увидел в расширении принципа эквивалентности сил инерции и сил тяготения на оптические явления.

Эквивалентность сил тяготения и сил инерции в классической механике была известна. Она следовала из факта равенства (как говорят сейчас) инертной и гравитационной масс. Еще Галилей установил, что все тела на Земле, если не учитывать сопротивление воздуха, падают с одним и тем же ускорением. Ньютон подтвердил этот вывод опытами с маятниками. В 1890 г. венгерский физик Этвеш проверил этот факт с большой степенью точности и подтвердил выводы Галилея и Ньютона. После открытия зависимости инертной массы от скорости вопрос о независимости ускорения силы тяжести от любых свойств тел и состояний, в которых они находятся, предстал в новом аспекте. Конечно, сразу нельзя было сказать, изменяются ли гравитационные свойства тел, если их инерционные свойства зависят от состояния движения.

В 1907 г. этот вопрос поставил Дж. Дж. Томсон. Он полагал, что инертная масса тела изменяется вместе с его движением вследствие изменения кинетической энергии эфира, связанного с телом. Но эфир, казалось бы, не должен был оказывать влияния на вес. Поэтому, предположил Томсон, отношение массы тела к его весу уже нельзя считать постоянным. Для проверки этой гипотезы Томсон решил сравнить период колебаний двух одинаковых маятников, чечевицы которых были изготовлены из радия и железа. Он полагал, что освобождаемая при распаде радия энергия имеет электромагнитное происхождение, поэтому часть массы радия нужно отнести за счет массы эфира, связанного сего атомами. Значит, инертная масса радия должна быть больше его гравитационной массы. Однако поставленный опыт был недостаточно точен для того, чтобы можно было сделать определенный вывод.

Позже (в 1910 г.) ученик Томсона Соутернс¹ проделал аналогичный опыт. Результаты его показали, что отношение массы к весу для радиоактивного тела такое же, как для нерадиоактивного.

В 1907 г. Планк² высказал мнение, что гравитационная и инертная массы всегда равны и имеют одну и ту же природу. Но так как согласно теории относительности энергия обладает инерцией, то она должна обладать и тяжестью.

В том же году этого вопроса коснулся Эйнштейн. В работе «О принципе относительности и его следствиях» он писал, что существование инертной массы у энергии «наводит на мысль о том, не обладает ли энергия также тяжелой (гравитирующей) массой. Далее напрашивается вопрос, ограничен ли принцип относительности системами, движущимися без ускорения»³. Ив этой работе, пока еще в предварительном, неразработанном, виде, Эйнштейн дает положительный ответ на эти вопросы.

В 1911 г. Эйнштейн уже подробно останавливается на данном вопросе и приходит к новым результатам и идеям, которые затем легли в основу общей теории относительности⁴. Эйнштейн подчеркивает, что две системы отсчета, одна из которой движется ускоренно, а другая хотя и покоится, но в ней действует однородное поле тяготения, в отношении механических явлений эквивалентны и неразличимы. В последующем этот факт Эйнштейн иллюстрирует примером, в котором наблюдатель, находящийся в закрытом лифте, не может определить, движется ли ускоренно лифт или внутри него действуют силы тяготения. Эквивалентность, существующую между ускорением и однородным полем тяготения, которая справедлива для механики, Эйнштейн считает возможным распространить на оптические и вообще любые физические явления. Этот расширенный принцип эквивалентности и был положен им в основу общей теории относительности. Но если распространить этот принцип эквивалентности на оптические явления даже для случая однородного поля тяготения, то мы уже придем к ряду следствий. Это явление красного смещения и отклонение светового луча под действием этого поля. Для того чтобы показать это и рассчитать соответствующие эффекты, Эйнштейн проводит простые, еще не достаточно строгие рассуждения; рассмотрим некоторые из них.

Представим инерциальную систему отсчета К⁰, которую можно считать находящейся в покое, и систему К', движущуюся относительно первой с постоянным ускорением j, направленным вдоль оси z (рис. 30). В начальный момент времени t = 0 системы совпадают друг с другом. Пусть в этот момент времени в системе К⁰ из точки S₂, находящейся на расстоянии h от начала координат S₁, начинает распространяться световое возмущение со скоростью с в направлении Пусть, далее, в тот момент времени, когда начала координат К⁰ и К' совпадают, скорость системы К' равна нулю. Тогда световое возмущение достигает точки S₁ в системе К⁰ за время t = h/c . За это же время система К’ приобретает скорость ѵ = jt. Если с>>v, то можно положить, что ѵ = jh/c.

Очевидно, что световое возмущение в инерциальной системе отсчета и в момент времени t=0, когда возмущение находится в точке S₂, и в момент времени t, когда оно приходит в точку S₁, имеет одну и ту же частоту,например ѵ₂. И паче обстоит дело в системе отсчета К'. В точку S₁ возмущение придет в момент времени t, когда система будет иметь скорость ѵ, следовательно, это излучение в системе К' уже имеет другую частоту ѵ₁.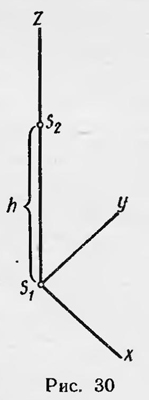

В первом приближении согласно принципу Доплера между этими частотами имеет место соотношение

ѵ₁= ѵ₂(1 + ѵ/с)=ѵ₂(1+hj/c²).

Введем теперь третью систему отсчета К, которая покоится относительно системы К⁰, по в которой действует однородное поле тяготения, и пусть гравитационный потенциал этого поля в точке S₂ на величину Ф = hj больше гравитационного потенциала в точке S₁. Тогда в силу принципа эквивалентности получим

v₁=v₂(1 +Ф/c₂).

Таким образом, если свет распространяется из точек с большим гравитационным потенциалом в точки с меньшим потенциалом, то его первоначальная частота увеличивается, и наоборот.

Этот вывод Эйнштейн обобщает на случай неоднородного гравитационного поля, сохраняя полученную формулу, и приходит к выводу о принципиальной возможности ее экспериментальной проверки.

Если, например, источник света, находясь на поверхности Солнца, излучает частоту ѵ₀, то это излучение придет на Землю c измененной частотой. Гравитационное поле Солнца гораздо больше, чем гравитационное поле Земли, поэтому разность потенциалов Ф имеет отрицательный знак и частота света, пришедшего на Землю, изменяется так, что соответствующие спектральные линии сместятся в направлении красной части спектра. Этот эффект красного смещения может быть проверен. Правда, Эйнштейн не уверен в практической возможности такой проверки.

Вывод об изменении частоты света при прохождении им поля тяготения приводит к заключению, что течение времени должно изменяться с изменением величины этого поля. Действительно, ведь при непрерывном излучении света источником, находящимся в пункте S₂, все исходящие гребни волн должны приходить в пункт S₁, при этом число гребней между этими пунктами не может изменяться. Это можно объяснить, говорит Эйнштейн, если принять, что ход часов и течение времени различны в этих пунктах. Там, где поле тяготения больше, часы идут медленнее в (1+Ф/с²) раз. Отсюда следует соответствующее изменение частоты света. Но если принять это утверждение, то из него следует, что скорость света уже не является постоянной величиной, а зависит от поля тяготения, в котором он распространяется. Если обозначить скорость света в начале координат через с₀, то скорость света с в некотором месте с гравитационным потенциалом Ф равна

с=с₀(1+Ф/с²).

Таким образом, получен новый фундаментальный результат: скорость света уже не является постоянной величиной, она изменяется, когда свет проходит поле тяготения, увеличиваясь или уменьшаясь в зависимости от взаимного направления распространения света и направления сил тяготения.

Отсюда, в частности, следует, что луч света, проходя мимо тела, обладающего сильным полем тяготения, должен искривляться, если его направление не совпадает с направлением силы тяготения. Этот эффект может быть обнаружен. При наблюдении солнечного затмения можно сравнить положение группы звезд, находящихся на небесной сфере вблизи Солнца во время его затмения (когда их можно наблюдать), с положением этой же группы звезд ночью. В первом случае световые лучи от этих звезд, проходя около поверхности Солнца, должны искривляться в его гравитационном поле, следовательно, наблюдаться смещенными относительно их обычного положения на небесной сфере.

«Было бы крайне желательным, чтобы астрономы заинтересовались поставленным здесь вопросом,—писал Эйнштейн,—даже и в том случае, если бы предыдущие рассуждения казались недостаточно обоснованными или фантастическими»⁵.

В последующие годы Эйнштейн, продолжая развивать изложенные идеи, создал новую теорию, которую назвал общей теорией относительности. Построение этой теории он закончил в 1916 г. При этом он использовал понятия и математический аппарат неевклидовых геометрий.

Рассмотрим в несколько произвольной форме самые общие и основные положения новой теории Эйнштейна. В основу общей теории относительности положен локальный принцип эквивалентности:

«Для бесконечно малых четырехмерных областей при подходящем выборе системы координат справедлива теория относительности в более узком смысле» (т. е. специальная теория относительности. — Б. С.).⁶

Это означает, что при наличии поля тяготения всегда можно выбрать такую систему отсчета К₀(х₁, х₂, х₃, х₄ = сt), относительно которой в бесконечно малой области пространства и времени движение материальной точки представляется свободным, т. е. прямолинейным и равномерным; свет распространяется относительно этой системы прямолинейно со скоростью с и т. д., т. е. все процессы протекают так же, как и в ннерциальной системе в случае отсутствия сил тяготения. В такой системе отсчета для данной бесконечно малой области пространства и времени «расстояние» между двумя бесконечно близкими точками выражается, как и в ннерциальной системе, свободной от поля тяготения:

dS² = dx²₁+dx²₂+dx²₃-dx²₄.

Однако во всякой другой системе отсчета К(х₁, х₂, х₃, х₄) элемент dS² определяется более сложно: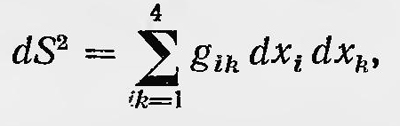

где g_ik — функции координат и времени — представляют собой компоненты так называемого фундаментального тензора G. При этом хотя выражение для dS имеет разный вид в разных системах отсчета, однако эта величина не зависит от их выбора, так что она является инвариантом для каждой точки пространства времени.

В отличие от системы отсчета Ко в любой другой системе координат К движение материальной точки, так же как и распространение светового луча, уже не является равномерным и прямолинейным, что воспринимается как результат действия поля тяготения.

Для разных точек пространства и времени dS определяют метрику четырехмерного многообразия (назовем его для краткости М-пространством). В отличие от четырехмерного пространства Минковского, введенного им при геометрической интерпретации специальной теории относительности, оно уже не обладает постоянной (нулевой) кривизной, Кривизна его меняется от точки к точке. Кривизна М-пространства определяется полем тяготения. Можно сказать больше: поле тяготения является не чем иным, как отклонением свойств М-пространства от свойств евклидова пространства и псевдоевклидова пространства Минковского. Величина поля тяготения в каждой точке определяется значением кривизны М-пространства в этой точке. Таким образом, движение материальной точки в поле тяготения можно рассматривать как свободное «инерциальное» движение, но происходящее уже не в евклидовом и не в псевдоевклидовом пространстве Минковского, а в М-пространстве G изменяющейся кривизной. В результате движение точки уже не является прямолинейным и равномерным, а происходит по геодезической линии М-пространства. Отсюда следует, что уравнение движения материальной точки, а также и луча света должно быть записано в виде уравнения геодезической линии М-пространства.

Для определения кривизны М-пространства необходимо и достаточно знать выражение для компонент фундаментального тензора G, который в теории Эйнштейна аналогичен потенциалу в теории тяготения Ньютона Задача, следовательно, заключается в том, чтобы, зная распределения тяготеющих масс в пространстве, определить g_ik тогда можно записать уравнение геодезической линии и решить проблему движения материальной точки, проблему распространения светового луча и т. д.

Эйнштейн решил эту задачу и нашел общее уравнение гравитационного поля, которое в классическом приближении переходило в закон тяготения Ньютона. Таким образом, проблема тяготения была решена им в общем виде. Рассматривая различные частные случаи, Эйнштейн вновь подтвердил, уточнил и исправил полученные им еще в 1911 г. результаты. Он получил более точное значение отклонения луча света при прохождении его около Солнца в поле тяготения последнего, а также подтвердил свой вывод о красном смещении спектров звезд по сравнению со спектрами земных источников света. Кроме того, решая задачу движения планет вокруг Солнца, он объяснил известные, но полностью не объясненные особенности движения перигелия Меркурия.

Новые идеи, высказанные Эйнштейном по мере создания общей теории относительности, вызывали дискуссии. Появляются работы, в которых подход к проблемам, которые рассматривал Эйнштейн, был иным. Некоторые теории имели полуклассический — полурелятивистский характер. Были ученые, которые на первых порах увидели в новых работах Эйнштейна отказ от основных, положений специальной теории относительности. Так, например, один из противников этой теории, Абрагам, усмотрел противоречие между общей теорией относительности, согласно которой скорость света не является постоянной, и прежним утверждением Эйнштейна о ее постоянстве, на основе которого был сформулирован специальный принцип относительности. Он писал с некоторым злорадством:

«... кто, подобно автору, неоднократно предостерегал от сиреноподобных песен этой теории (специальной теории относительности.— Б. С.), тот может с удовлетворением приветствовать, что сам основатель теории убедился в ее несостоятельности»⁷.

События первой империалистической войны в значительной степени ослабили дискуссию, разгоревшуюся вокруг общей теории относительности, так же как и вокруг специальной теории относительности. Только после окончания войны она развернулась с новой силой и вскоре приняла в силу целого ряда обстоятельств весьма острый характер.

Большое значение для широкого признания общей теории относительности, а вместе с ней и специальной теории относительности, имели опыты по измерению отклонения лучей света, проходящих около Солнца. Как уже говорилось, Эйнштейн еще в 1911 г. высказал пожелание проверить выводы теории, наблюдая положение группы звезд во время затмения Солнца. В 1914 г. немецкие астрономы направились для наблюдения полного солнечного затмения, рассчитывая проверить предсказанный Эйнштейном эффект отклонения лучей света в поле тяготения Солнца. Однако начавшаяся война помешала этому. В 1919 г. одна английская экспедиция направилась в Бразилию, а другая — на один из островов, расположенных возле африканского материка, для проверки этого эффекта. Наблюдения обеих экспедиций подтвердили существование эффекта Эйнштейна. Предполагаемое смещение группы звезд, видимых около Солнца во время затмения, действительно имело место, хотя точность измерений была невелика. Проведенные в 1922 г. измерения также подтвердили существование эффекта, предсказанного теорией Эйнштейна.

Подтверждение выводов теории Эйнштейна способствовало усилению интереса к этой теории. Теорией заинтересовались не только специалисты-ученые, но и философы, писатели, журналисты, духовенство и т. д. Публикуется огромное число статей, брошюр и книг, посвященных научному и научно-популярному изложению теории относительности. Появляются исследования, посвященные изложению философских выводов из этой теории. Зоммерфельд в 1920 г. писал:

«Никогда еще в памяти людей научная теория не обсуждалась таким» широкими кругами, как теория относительносги Эйнштейна»⁸.

То же самое отметил советский физик А. К. Тимирязев, который в одном из своих докладов сказал:

«Без всякого преувеличения можно сказать, что никогда еще за все время существования нашей науки ни одна из ее текущих задач, ни одна теория не привлекала к себе такого внимания, как теория относительности, разработанная Альбертом Эйнштейном; в наши дни об этой теории заговорили решительно везде: ею заинтересовались люди, стоящие совершенно в стороне от научной жизни и, быть может, до настоящего момента остававшиеся совершенно равнодушными к текущим задачам такой науки, как физика»⁹.

Однако всеобщий интерес к теорий относительности еще не означал всеобщего ее признания. По-прежнему среди ученых и философов имелись противники этой теории. Наиболее активные из них объявили результаты наблюдений солнечных затмений 1919 и 1922 гг. сомнительными. Высказывались предположения, что наблюдаемое смещение звезд обусловлено несовершенством приборов и погрешностями измерений. Некоторые сомневались в правильности полученных количественных данных. Существовало мнение, что результаты измерений противоречат теории Эйнштейна, но подтверждают теории, появившиеся ей в противовес, которые основывались на классических представлениях. Эти теории также приводили к выводу об искривлении световых лучей в поле тяготения, хотя и давали несколько иное количественное значение, нежели то, которое следовало из теории Эйнштейна¹⁰.

Противники теории относительности выступили с возражением против других подтверждений этой теории. Речь идет об объяснении, данном Эйнштейном на основании выводов из общей теории относительности, аномалий в движении Меркурия. Было известно, что орбита Меркурия с течением времени совершает поворот в своей плоскости, так что ее перигелий смещается за 100 лет на угол, равный 572,70”. Частично этот эффект объяснялся возмущающими действиями других планет, но оставался необъясненным поворот перигелия, равный 42,56"±0,5". Общая теория относительности объясняет этот факт. Она давала значение 43"±0,03", что, вообще говоря, хорошо соответствовало наблюдению. Однако в результате последующих уточнений движения Меркурия как будто указанная выше цифра была уменьшена до 29"—38", так что уже о полном совпадении теории с опытом говорить было нельзя¹¹.

Кроме того, поскольку аномалия в движении Меркурия была известна давно, то уже существовали теории, объясняющие эту аномалию. Они были основаны на совсем других гипотезах, нежели гипотеза Эйнштейна, и имели чисто классический характер.

Третий результат, полученный в теории Эйнштейна, — наличие красного смещения в спектрах небесных тел — был подтвержден Сент-Джоном в 1923—1926 гг. при наблюдении спектра Солнца. В 1925 г. Адамс подтвердил выводы теории, наблюдая спектр спутника Сириуса, обладающего чрезвычайно большим полем тяготения. Однако их тонкие и тщательные эксперименты подверглись сомнению противниками теории относительности. Кроме того, были предложены новые теории, объясняющие наличие красного смещения в спектрах небесных тел, которые были основаны на совершенно иных представлениях, не имеющих никакого отношения к теории относительности.

Помимо попыток опровергнуть экспериментальные результаты, подтверждающие теорию Эйнштейна, возникла мысль о необходимости проверить выводы опыта Майкельсона. Появились работы, в которых доказывалось, что теория опыта Майкельсона неправильна, что более правильная теория этого не противоречит выводу о наличии эфирного ветра на Землю. Кроме того, подверглись сомнению результаты этого опыта. Американский физик Миллер предпринял в 1921— 1925 гг. серию экспериментов, являющихся повторением опыта Майкельсона. Опыты Миллера как будто бы дали положительный эффект. Миллер писал, что они «приводят к заключению, что существует определенное смещение интерференционных полос, такое, какое было бы вызвано относительным движением Земли и эфира... со скоростью приблизительно 10 км/с»¹². Результаты, полученные Миллером, противоречили теории относительности. Однако они не могли быть объяснены и с точки зрения теории эфира. Больше того, эти результаты не объяснялись никакой существующей теорией и являлись, по-видимому, результатом каких-то дефектов в приборах или несовершенством методов измерений. Тем не мёнее противники теории относительности использовали результаты, полученные Миллером. Так, например, А. К. Тимирязев писал:

«Вопрос вступил в новую фазу — теперь уже ни Эйнштейн, ни кто другой не запугают тем, что «опыт принципиально не может дать положительного результата». Вера в догмат теории Эйнштейна подорвана»¹³.

В 1926 г. опыт Майкельсона был повторен Кеннеди. В том же году Пиккар и Стаэль провели опыт Майкельсона на воздушном шаре, а также в лабораторных условиях. В 1927 г. Иллингворт еще раз повторяет опыт Майкельсона. Все эти опыты дали прежний результат: никакого эфирного ветра на Земле не было обнаружено. Таким образом, надежда противников теории относительности получить в опыте Майкельсона какой-либо положительный эффект оказалась тщетной. Оставалась лишь возможность иного толкования результата опыта Майкельсона, и часть противников теории относительности пошла по этому пути. Однако с течением времени все большее и большее число физиков становилось на точку зрения теории относительности, как специальной, так и общей.

¹ Southerns L. Proc. Roy. Soc., (A), vol. 84, 1910, p. 385. См. также: «Новые идеи в физике». Сб, 2, 1916, с. 99.
²Планк М. Избранные труды. М., Изд-во АН СССР, 1975, с. 466.
³Эйнштейн А. Собрание научных трудов. Т. I, с. 67.
⁴Эйнштейн А. Собрание научных трудов. Т. I, с. 165.
⁵Эйнштейн А. Собрание научных трудов. Т. I, с. 174.
⁶Там же, с. 460.
⁷Лоренц Г.,Пуанкаре А.,Эйнштейн А.,Минковский Г. Принцип относительности. М., ОНТИ, 1935, с. 371.
⁸Sommerfeld A. iMünchener med. Wochenschr. Bd. 67, 1920, S. 1268.
⁹Тимирязев A. K. Естествознание и диалектический материализм. М., 1925, с. 46.
¹⁰Впоследствии эффект Эйнштейна проверялся еще несколько раз (в 1929, 1936, 1952 гг.). О результатах всех подобных наблюдений высказывались разные мнения. Так, например, в 1924 г. астроном Эсклангон, говоря о первых измерениях эффекта Эйнштейна, писал:
«...наблюдения не подтверждают и не опровергают закон отклонения Эйнштейна. Они Щшь указывают, если отбросить всякие предположения о систематических ошибках, на существование отклонений около Солнца, но без определения закона и без точной величины отклонения у солнечного края».
В 1956 г. советский астроном А. А. Михайлов, обсуждая результаты измерений, имевших целью проверить эффект Эйнштейна, приведя эту цитату, указывал:
«Эти слова, быть может в смягченной форме, остаются справедливыми н поныне, несмотря на ряд наблюдений, произведенных в последующие годы» (Михайлов А. А. Наблюдения эффекта Эйнштейна во время солнечного затемнения.— В кн.: Эйнштейн и современная физика. М.—Л., Гостехиздат, 1955, е. 157—158).
В совсем недавно вышедшей работе «Физические принципы общей теорі и относительности» Сиама пишет:
«По иронии судьбы предсказание Эйнштейна отнюдь не было подтверждено столь убедительно, как это считалось» (Сиама Д. Физические принципы общей теории относительности. М., «Мир», 1971, с 74).
С другой стороны, еще в 1928 г. С. И. Вавилов считал, что:
«Смещение звезд около Солнца, предсказанное общей теорией относительности, подтверждается как с качественной, так и с количественной стороны» (Вавилов С. И. Экспериментальные основания теории относительности. М.—Л., Госиздат, 1928, с. 134).
Уже в 1956 г. В. Л. Гинзбург пишет:
«Наблюдения во время полных затмений привели к обнаружению отклонения световых лучей, проходящих вблизи Солнца, причем предсказания теории подтвердились в пределах достигнутой точности эксперимента, которая равна примерно 10%.» (Гинзбург В. Л. Экспериментальная проверка общей теории относительности.— В кн. Эйнштейн и современная физика, с. 137).
¹¹См.: ВавиловС. И. Экспериментальные основания теории относительности, с. 141. В этой книге он писал:
«Временно вопрос о строгой количественной стороне дела остается открытым, и можно сказать только, что в отношении порядка величины теория Эйнштейна удовлетворительно объясняет аномалию движения Меркурия».
Однако в последующем было показано, что существует хорошее совпадение теории с результатами наблюдения в данном вопросе (см., например: Гинзбург В. Л. Экспериментальная проверка общей теории относительности. — В кн.: Эйнштейн и современная физика, с. 99).
¹²Миллер Д. К. Эфирный ветер.— УФН, т. 5, 1925, с. 185.
¹³Тимирязев А. К. Теория относительности Эйнштейна и диалектический материализм.— «Под знаменем марксизма», 1924, № 8—9, с. 151.

<<Назад Вперёд>>

Просмотров: 3776

загрузка...

Другие книги по данной тематике