§ 59. Развитие классической электродинамики после Максвелла

Развитие классической электродинамики после Максвелла шло по нескольким направлениям, из которых отметим два основных. Во-первых, совершенствовалась математическая сторона теории Максвелла и были получены некоторые новые результаты. Во-вторых, произошло объединение теории электромагнитного поля с основными идеями теории строения вещества. Последнее направление привело к созданию электронной теории. Рассмотрим развитие этих направлений.

Систематизацией уравнений Максвелла и приведением их к современному виду занимались в первую очередь Герц и английский ученый Хевисайд. Герц в 1884 г., еще не будучи уверенным в истинности теории Максвелла, выделил из всей системы его уравнений два основных и записал их для напряженностей электрического и магнитного полей так, как их пишут и сейчас в случае отсутствия токов и для пустого пространства. Правда, Герц еще не пользовался векторным обозначением, а писал уравнение в координатной форме. В современных обозначениях они имеют вид:

Одновременно с этими основными уравнениями Герц также использует два других уравнения Максвелла применительно к пустому пространству, а именно:

divH = 0, divE=0.

Герц, как отмечено выше, еще не уверен в правоте теории Максвелла, однако все же отдает ей предпочтение по сравнению с электродинамикой, разработанной Вебером и Нейманом. Нужно подчеркнуть, что Герц в данной работе не просто систематизирует уравнения Максвелла, но и обосновывает их. При этом он не строит моделей и не основывается на гипотезе о токе смещения и т. п., как это делал Максвелл. Герц получает уравнение Максвелла, исходя из задачи усовершенствования электродинамики. Он указывает, что ее нельзя считать полной. Существующая теория устанавливает наличие пондеромоторных сил между токами в зависимости только от сил токов и конфигурации проводников, тогда как они должны зависеть и от скорости изменения сил токов, следовательно, и от производных этих сил токов по времени. Действительно, в результате изменения силы тока в одном из проводников, согласно явлению электромагнитной индукции, в других проводниках возникают индукционные токи, т. е. движение электрических зарядов. Однако это движение возникает и под действием «электростатического» заряда, поэтому в каждый данный момент действие переменного тока на проводник эквивалентно в известной степени действию электрической силы, создаваемой некоторым распределением в пространстве электрических зарядов. Отсюда, учитывая закон равенства действия противодействию, можно сделать вывод, что должно существовать и обратное действие электрического заряда или электрических зарядов на проводник, по которому течет переменный электрический ток, и, наконец, прийти к заключению, что между переменными токами должны действовать силы, помимо тех, о которых говорит закон Ампера. Но такого рода силы не принимались во внимание существующей теорией и Герц старается их учесть. При этом он и приходит к уравнениям Максвелла. Мы не имеем возможности остановиться на соображениях Герца, следуя которым он приходит к уравнениям Максвелла, и отсылаем интересующихся к его оригинальной работе¹. Укажем только, что определенную роль в соображениях Герца играл принцип симметрии между вектором напряженности электрического и магнитного полей.

В 1889 г., уже после обнаружения электромагнитных волн, Герц создает теорию излучения «вибратора Герца». При этом он использует уравнения Максвелла в том же виде, что и в упомянутой выше работе, и опять для пустого пространства. Наконец, в 1890 г. в работе, посвященной электродинамике покоящихся тел, Герц вновь пишет четыре уравнения Максвелла в случае пустого пространства для напряженности полей, а затем обобщает их на неподвижные среды. Он вводит диэлектрическую и магнитную проницаемость, векторы электрической и магнитной индукции и т.д. Эта работа Герца носит методический характер. В ней он записывает уравнения Максвелла близко к современной форме.

Систематикой уравнений Максвелла занимался параллельно с Герцем, как отмечалось, также Хевисайд. Он также выделяет два основных уравнения и исключает в одном из них вектор-потенциал. Однако в отличие от Герца Хевисайд в первой же работе, посвященной теории Максвелла (1885), записывает уравнения Максвелла для общего случая. В компактной форме эти уравнения Хевисайд приводит в 1888 г. К системе уравнений Хевисайд относит следующие уравнения (если их записать в порядке, наиболее соответствующем порядку написания этих уравнений в настоящее время):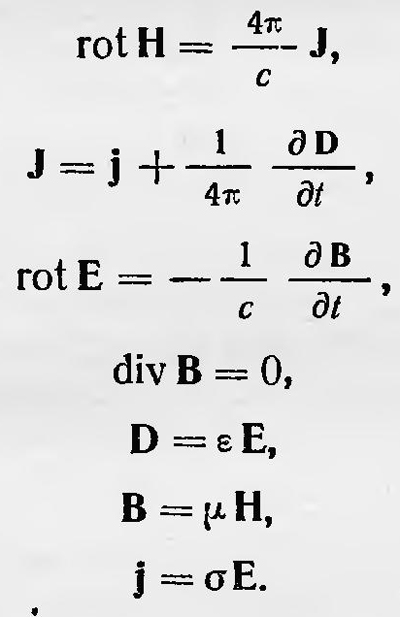

Как мы видим, система уравнений Максвелла, написанная Хевисайдом, имеет почти современный вид, только в ней отсутствует уравнение divD = 4πρ.

Более принципиальное значение для развития теории Максвелла имели работы англичанина Пойнтинга (1884) и Хевисайда (1885). В них был рассмотрен вопрос о движении энергии электромагнитного поля и получено выражение для вектора потока энергии электромагнитного поля. Следует отметить, что исследования Пойнтинга и Хевисайда являлись развитием, или, точнее, конкретизацией, работ Умова о движении энергии, в которых он впервые в общей форме исследовал вопрос локализации и движения энергии. В связи с этим в нашей литературе нередко вектор потока энергии электромагнитного поля называют вектором Умова — Пойнтинга². Однако Пойнтинг и Хевисайд нигде не ссылаются на Умова. То же можно сказать и о ряде последующих зарубежных работ, в которых ставился вопрос и о движении энергии в общем виде. Причем в этих работах, считающихся нередко обобщением идеи Пойнтинга, не учитывается, что общая теория о движении энергии была разработана Умовым³.

Позже, уже в конце XIX в., наряду с вектором потока энергии электромагнитного поля возникло и представление об импульсе электромагнитного поля. Впервые мысль о существовании импульса электромагнитного поля высказал Дж. Дж. Томсон, исходя из построенной им механической модели электромагнитного поля. Он указал, что одновременно с переносом энергии в электромагнитном поле должен иметь место и перенос импульса. При этом вектор импульса g связан с вектором Умова — Пойнтинга Р соотношением

q=P/c².

В 1900 г. Пуанкаре указал, что, для того чтобы сохранить третий закон Ньютона в электродинамике в случае наличия электромагнитного поля, необходимо ввести количество движения эфира (электромагнитного поля), которое должно быть пропорционально вектору потока энергии этого поля. Более подробно этот вопрос был исследован немецким физиком М. Абрагамом в 1902 г. Наконец, в 1898 г. русский физик А И. Садовский теоретически показал, что эллиптически поляризованный свет должен обладать вращательным моментом. Так, например, если кристалл преобразует эллиптически поляризованный свет в плоскополяризованный, то на этот кристалл должен действовать вращательный момент.

Экспериментальным подтверждением существования количества движения у электромагнитного поля явились опыты П. Н. Лебедева по измерению светового давления на твердые тела, повторенные позже другими физиками. Опытное подтверждение существования момента импульса у эллиптически поляризованного света было получено позже. Только в 1935 г. впервые американец Бет экспериментально обнаружил эффект Садовского.

Перейдем теперь к истории развития электронной теории, которая начинается с зарождения гипотезы о том, что с частицами вещества связаны электрические заряды. Впервые эта идея зародилась в процессе изучения электролиза. Шведский химик И. Берцелиус в начале XIX в., изучая явление электролиза, пришел к мысли о том, что атомы химических элементов несут электрический заряд. Эту гипотезу он положил в основу своей теории химического сродства.

Фарадей, занимавшийся изучением электролиза и открывший его основные законы, отметил, что с каждым атомом вещества должен быть связан определенный электрический заряд. Это следует из закона, согласно которому существует постоянное соотношение между величиной прошедшего заряда и количеством перенесенного к электродам вещества. Он писал:

«... если принять атомную теорию и соответствующие ей выражения, то атомы тел, эквивалентные друг другу в отношении их обычного химического действия, содержат равное количество электричества, естественно связанное с ними. Но я должен сознаться, что с некоторым подозрением отношусь к термину атом, так как хотя об атомах очень легко говорить, но весьма трудно составить себе ясное представление об их природе, особенно когда дело идет о сложных веществах»⁴.

Последнее добавление связано с общими взглядами на природу материи Фарадея, о которых говорилось выше. Это добавление никак не отрицает гипотезу о том, что с атомом вещества связано определенное количество электричества. Нужно только учитывать, что такое атом в понимании Фарадея.

Независимо от Фарадея на основании совсем других соображений к идее об элементарном электрическом заряде, пришел Вебер, который в начале 70-х годов высказал идею о том, что с каждым весомым атомом связан электрический атом (о взглядах Вебера мы скажем ниже).

Идеи, высказанной Фарадеем, коснулся Максвелл. Он писал:

«Для удобства описания мы можем называть этот постоянный молекулярный заряд (обнаруженный опытами Фарадея) одной молекулой электричества». Однако далее добавляет: «Крайне невероятно, чтобы мы удержали в той или иной форме теорию молекулярных зарядов, если нам удастся понять истинную природу электролиза, так как тогда у нас будет надежная основа, на которой можно построить правильную теорию электрических токов и таким образом освободиться от этих временных гипотез»⁵.

Иначе об идее Фарадея отозвался Гельмгольц. В 1881 г. он в речи, посвященной памяти Фарадея, сказал:

«Если применить эту гипотезу к электрическим процессам, то она, в соединении с законом Фарадея, приводит к поразительным следствиям. Если мы допускаем существование химических атомов, то мы принуждены заключить отсюда далее, что также и электричество, как положительное, так и отрицательное, разделяется на определенные элементарные количества, которые играют роль атомов электричества»⁶.

На высказывание Фарадея обратил также внимание англичанин Дж. Стоней в докладе, прочитанном в 1874 г., Но опубликованном в 1881 г. Этот доклад был посвящен вопросу выбора основных физических единиц. В качестве универсальной основной системы единиц Стоней предложил принять «естественную» систему, а именно: скорость света, постоянную тяготения и электрический элементарный заряд. Существование электрического элементарного заряда, по мнению Стонея, следует из законов электролиза и основных положений молекулярной теории. Пользуясь ими, можно не только прийти к мысли о возможном выборе естественной единицы электричества, но и определить ее значение. Стоней произвел простой расчет. Зная величину электрохимического эквивалента водорода (количество водорода, выделяемого при электролизе зарядом в один кулон), удельный вес водорода и, наконец, число атомов водорода в 1 см³ при нормальных условиях (число Лошмидта), Стоней определил, что один атом водорода при прохождении тока через электролит несет заряд, равный приблизительно 10^-20 СГСМ (по современным данным, заряд электрона равен 1,602033 10^-20 СГСМ). Через несколько лет, в 1891 г., Стоней вновь вернулся к вопросу об элементарном электрическом заряде и предложил назвать его электроном. Он писал, что «эти заряды, которые удобно назвать «электронами», не могут быть отделены от атомов»⁷.

На мысль о корпускулярном строении электричества наводили также результаты, полученные при изучении электрических явлений в газах. Прохождение электричества через газы и связанные с этим процессом явления наблюдали в лабораторных условиях еще в середине XVIII в. Однако систематически эти явления начали изучать значительно позже, в середине XIX в.

В 1838 г. Фарадей, рассматривая прохождение электричества через разреженный газ, установил, что свечение, сопровождающее такой разряд, имеет определенную структуру. Теорию этого явления Фарадей не разработал, но указал, что результаты таких наблюдений в будущем «окажут на теорию учения об электричестве значительно большее влияние, чем мы можем себе представить в настоящее время»⁸.

Начиная с 50-х годов, после того как немецкий стеклодув Гейслер стал изготовлять газоразрядные трубки (носящие его имя), изучение разрядов в газах пошло интенсивнее. В 1858—1859 гг. Плюккер, исследуя электрический разряд в таких трубках, открыл существование катодных лучей. Он заметил, что если катод сделан в виде острия, то свечение имеет форму шнура, отходящего от катода. Этот «шнур» отклонялся магнитным полем. Плюккер пришел к заключению, что это поток заряженных частиц, летящих от катода к аноду. Он заметил также, что стекло возле катода начинало светиться.

Исследования ряда физиков подтвердили установленные Плюккером факты и дополнили их новыми; лучи, наблюдавшиеся Плюккером, получили название катодных лучей. Многие физики, так же как и Плюккер, полагали, что катодные лучи - это поток заряженных частиц. О природе этих частиц единого мнения не существовало. Так, например, Крукс, занимавшийся в 70-х годах исследованием катодных лучей, пришел к мнению, что катодные лучи являются потоком особых отрицательно заряженных частиц и представляют собой некое четвертое состояние материи. Другие же считали, что катодные лучи — это поток обычных частиц (атомов или молекул), несущих электрический заряд. Были и такие физики, которые считали катодные лучи возмущением, распространяющимся в эфире подобно световым волнам. Так, например, Герц, который находился еще под влиянием теории Гельмгольца, допускавшей существование не только поперечных, но и продольных электромагнитных волн, считал катодные лучи продольными волнами в эфире. В 1883 г. Герц проделал эксперимент, имевший целью определить, обладают ли катодные лучи магнитным и электрическим действием, и получил отрицательный результат. Скоро, однако, было обнаружено что, эти результаты ошибочны.

К 80-м годам было окончательно выяснено, что газы не являются абсолютными изоляторами и, хотя и слабо, проводят электрический ток; проводимость их можно увеличить, подвергнув, например, нагреванию. Было высказано мнение, что, подобно проводимости электролитов, проводимость газов объясняется наличием заряженных частиц ионов. Такую точку зрения подробно развил в 1882 г. Гизе. Согласно его теории, в газах всегда имеется некоторое количество заряженных частичек, образующихся в результате деления молекул на положительные и отрицательные частицы-ионы, которые, так же как и в жидкостях, проводят электричество. Однако в обычных условиях таких ионов в газах очень мало. При более высоких температурах их число увеличивается и проводимость повышается. К этой теории присоединился и английский физик Шустер, который считал, что частицы газов — ионы — всегда несут определенный электрический заряд. Продолжая свои исследования, Шустер попробовал проверить эту теорию на опыте и одновременно определить отношения заряда к массе таких ионов. Для этого он решил использовать явление отклонения катодных лучей в магнитном поле. Если частица массы m, имеющая заряд е, движется со скоростью ѵ, то, попадая в магнитное поле, напряженность которого Я перпендикулярна направлению скорости этой частицы, она должна изменить свою прямолинейную траекторию и двигаться по дуге окружности, радиус которой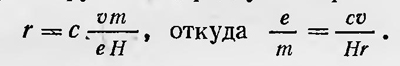

Предположим, что вся скорость, полученная частицей в катодных лучах, определяется разностью потенциалов <р на аноде и катоде, тогда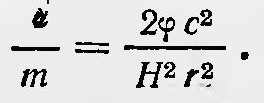

Таким образом, зная напряженность магнитного поля Н, разность потенциалов φ, измерив отклонение катодных лучей в магнитном поле и определив r, можно вычислить отношение заряда к массе для катодных частиц. Такой эксперимент и проделал Шустер, получивший, что е/m ≈ 0,3*10²СГСМ. Этот результат показался Шустеру сомнительным. Он полагал, что отношение е/т в катодных лучах должно быть по порядку величины равно отношению е/m для иона водорода, подсчитанному из данных электролиза, т. е. более 2000 СГСМ.

«... Я мог отсюда заключить,— пишет Шустер,— что или количество электричества, переносимое при разряде в газах, значительно больше переносимого ионами при электролизе, или что масса его «носителя» гораздо меньше»⁹.

Однако Шустер такого заключения в свое время не сделал, его исследования были опубликованы в 1890 г., но не обратили на себя внимания.

Гендрик Антон Лоренц

Наконец, была высказана и гипотеза о том, что ток проводимости осуществляется в результате движения дискретных зарядов. Эта идея принадлежала Фехнеру, а затем была развита Вебером, о работах которого уже упоминалось. Первоначально Вебер не обсуждал вопрос о связи «атомов электричества» с атомами веществ, но затем ему пришлось приписать электрическим частицам массу. Это было сделано в период дискуссии с Гельмгольцем об отношении его теории к закону сохранения энергии. В 1871 г. он писал, что с «каждым весомым ионом связан электрический атом». Применяя указанную гипотезу, Вебер пытался объяснить ряд явлений, связанных с электрическим током, в том числе выделение током тепла в проводниках, термоэлектричество, явление Пельтье и др. При этом ему удалось предвосхитить ряд положений, установленных позже в электронной теории.

Начиная с 70-х годов XIX в. разработкой электронной теории занялся Гендрик Антон Лоренц (1853—1928), объяснивший с ее помощью электромагнитные и оптические явления. Он исходил из того, что теория Максвелла нуждается в дополнении, так как в ней не учитывается структура вещества. Вспоминая причины, побудившие его к разработке теории электронов, Лоренц впоследствии писал:

«... действительно, ведь в этой общей теории (т. е. в теории Максвелла.— Б. С.) мы, чтобы выразить особенные свойства различных весомых іел, просто приписываем каждому из них специальные значения диэлектрической постоянной«, проводимости а и магнитной проницаемости μ. Если мы хотим понять, каким образом электрические и магнитные свойства зависят от температуры, плотности, химического строения или кристаллического состояния вещества, то мы не можем удовлетвориться простым введением для каждого вещества этих коэффициентов, значения которых должны определяться из опыта; мы будем принуждены обратиться к какой-нибудь гипотезе относительно механизма, лежащего в основе всех этих явлений.

Эта необходимость и привела к представлению об электронах, т. е. малых электрически заряженных частичках, которые в громадном количестве присутствуют во всех весомых телах...»¹⁰.

С самого начала научной деятельности Лоренц уделяет особенно большое внимание исследованиям по оптике, в том числе и молекулярной оптике.

Как мы видели выше, уже в период создания волновой теории света было выяснено, что для объяснения явления дисперсии света нужно признать, что среда, в которой распространяется свет, имеет атомистическое строение. Уже тогда начинает зарождаться молекулярная теория дисперсии. Частицы вещества начинают рассматривать как элементарные осцилляторы, которые под действием проходящих световых волн совершают колебательные движения.

Эту теорию развивает уже в 1878 г. Лоренц. При этом он уже пользуется электромагнитной теорией света и считает молекулы вещества состоящими из электрических зарядов, которые могут поляризоваться и совершать колебания под влиянием проходящей электромагнитной волны. Лоренц получает формулу для показателя преломления света n: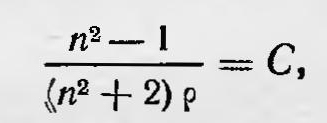

известную под названием формулы Лоренц—Лоренца. Это название объясняется тем, что формула была получена одновременно однофамильцем Лоренца Л. Лоренцем, который исходил из несколько иных соображений.

В первой половине 90-х годов Лоренц уже выступает в печати1¹¹ с общей теорией электромагнитных и оптических явлений, опирающейся, с одной стороны, на теорию Максвелла, а с другой стороны, на представление о существовании элементарных электрических зарядов, связанных с частицами вещества. Эта теория впоследствии (после открытия электрона) получила название электронной теории.

Заряженные частицы вещества, называемые Лоренцем ионами, вызывают в окружающей их среде, т. е. в эфире, особое состояние, которое определяется значениями напряженности электрического е и магнитного h полей. Величина и изменение этих полей со временем определяются уравнениями Максвелла, которые, учитывая, что электрический ток является движением электрических зарядов, можно записать для эфира и находящихся в нем ионов следующим образом:

Здесь v — скорость движения частиц, ρ — плотность электрического заряда.

Заряженная частица (ион, находящийся в электрическом и магнитном полях) должна испытывать действие силы, которая зависит от значений е и h в точке ее нахождения, а также и от скорости ее движения. Эта сила — сила Лоренца, действующая на единицу заряда — равна

F = е + 1/с [ѵh].

Непосредственно применять уравнение Лоренца для описания электромагнитных процессов в макроскопических масштабах в случае наличия среды нельзя (в вакууме же они совпадают с уравнениями Максвелла). Величины е и h изменяют свои значения уже на расстоянии атомных размеров и притом чрезвычайно быстро, так что доступные измерению значения электрических и магнитных полей представляют собой средние значения этих величин. Поэтому, чтобы иметь возможность применять уравнения Лоренца для макроскопических полей, их нужно усреднить. Учитывая, что е = Е и h = В, получаем для немагнитных сред из уравнений Лоренца следующие уравнения: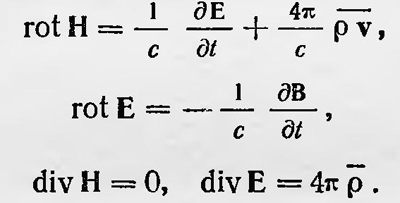

Если теперь определить значения ρѵ и ρ для случая неподвижных сред, то получим обычные уравнения Максвелла. В случае, когда среда обладает магнитными свойствами, усреднение уравнений Лоренца более сложно, но и тогда для неподвижных сред приходим к уравнениям Максвелла.

Для случая же, когда среда движется как целое, усреднение уравнений Лоренца приводит к новым уравнениям, их Лоренц считает уравнениями для движущихся сред. Нужно отметить, что разработка Лоренцем электронной теории в значительной степени была обусловлена попыткой создать электродинамику движущихся сред. Этим и обусловлено название его главного труда «Опыт теории электрических и оптических явлений в движущихся телах». Электродинамике движущихся сред посвящена специальная глава, в которой рассмотрена роль Лоренца в развитии этой области физики. Сейчас же ограничимся только рассмотрением развития электронной теории для неподвижных сред.

Первым серьезным успехом новой теории было объяснение открытого в 1896 г. учеником Лоренца Зееманом явления расщепления спектральных линий в магнитном поле. Первоначальная установка Зеемана не была снабжена достаточно точной аппаратурой, и Зееман заметил, только, что спектральные линии расширяются, если источник света помещен в магнитное поле. Узнав результаты первого опыта Зеемана, Лоренц объяснил их, исходя из теории электронов. При этом он предсказал, что спектральные линии в опыте Зеемана должны не просто расширяться, но разделяться на две или на три в зависимости от направления, в котором производится наблюдение по отношению к направлению магнитного поля. Лоренц также определил, что эти линии должны быть определенным образом поляризованы. Последующие экспериментальные исследования подтвердили выводы Лоренца и, таким образом, явились подтверждением электронной теории.

Вскоре после создания электронной теории была развита электронная теория металлов. Немецкий физик Друде полагал, что электроны, находящиеся в металле, являются свободными и ведут себя подобно атомам идеального газа. Эта гипотеза дала ему возможность, применив методы кинетической теории газов к электронам внутри металла, построить электронную теорию металлов, которая была далее разработана Лоренцем в 1904—1907 гг.

Новые результаты были получены также при применении электронной теории для объяснения магнитных свойств тел. Магнитные свойства парамагнетиков объяснились еще старой теорией, согласно которой молекулы парамагнетиков имеют постоянный магнитный момент, т. е. представляют собой маленькие магниты. При отсутствии магнитного поля магнитные моменты молекул расположены хаотически, так что общий магнитный момент всего тела равен нулю. В случае же магнитного поля молекулы принимают преимущественную ориентацию и тело приобретает магнитный момент.

О диамагнетизме были высказаны идеи Вебером, а затем Максвеллом. Максвелл полагал, что в молекулах диамагнетиков при возникновении магнитного поля согласно закону электромагнитной индукции возникают электрические токи. При этом магнитный момент возникших токов имеет направление, противоположное направлению напряженности магнитного поля.

Развитие представлений об электронах поставило на очередь задачу рассмотреть явление парамагнетизма и диамагнетизма с точки зрения этой теории. Впервые электронную теорию диамагнетизма начал разрабатывать английский ученый Лармор, который одновременно с Лоренцем участвовал в построении общей теории электронов. Лармор объяснил явления диамагнетизма, рассматривая движение электронов в веществе, учитывая при этом действие внешнего магнитного поля (прецессия Лармора).

В 1905 г. Ланжевен развил более подробную и строгую электронную теорию диамагнетизма и парамагнетизма. Электронная теория ферромагнетизма была разработана Вейсом (1907).

¹Hertz H. Gesamelte Werke. В. S. Leipzig, 1895, S. 295. См. также: Григорьян А. Т., Вяльцев А. Н. Генрих Герц. М., «Наука», 1968, с. 35.
²О См., например: Калашников С Г. Электричество. М., «Наука», 1970, с. 609.
³Подробно по этому вопросу см. в ки.: Гуло Д. Д. Николай Алексеевич Умов. М., «Наука», 1971.
⁴>) Фарадей М. Экспериментальные исследования по электричеству. Т. I. М., Изд-во АН СССР, 1947, с. 344.
⁵Миллике Р. Электроны, протоны, фотоны, нейтроны и космические лучи. М. —Л., ГОНТИ, 1939, с. 23—24.
⁶Гельмгольц Г. Популярные речи. Т. I. Изд. 2. СПб., 1898, с. 124
⁷Stопеу G. Sei. Trans. Roy. Dublin (2). Vol. 4, 1891, p. 563.
⁸Фарадей М. Экспериментальные исследования no электричеству. Т. I, с. 638.
⁹Шустер А. Прогресс физики. Пг., 1915, с. 70.
¹⁰Лоренц Г. Теория электронов и ее применение к явлениям света и теплового излучения. М., Гостехиздат, 1953, с. 28—29.
¹¹Наиболее известной работой Лоренца этого периода является: «Versuch einer Theorie der electrischen und optischen Erscheinungen in bewegten Körpern*. Leiden, 1895.

<<Назад Вперёд>>

Просмотров: 5086

загрузка...

Другие книги по данной тематике