§ 57. Возникновение теории электромагнитного поля
|
К середине XIX в. физика электрических и магнитных явлений достигла известного завершения. Был открыт ряд важнейших законов: закон Кулона, закон Ампера, закон электромагнитной индукции, законы постоянного тока и др. Теоретические представления также развились в стройную общую концепцию, основанную на представлении о дальнодействии. Вершиной развития теории электрических и магнитных явлений, основанной на этой концепции, была теория Вебера, которая объединила и электростатику, и электромагнетизм того времени. Не существовало, казалось, никаких оснований для революционного переворота в физике электрических и магнитных явлений. Правда, полного единства во взглядах физиков на электрические и магнитные явления не было. Была еще концепция Фарадея, которая резко отличалась от взглядов остальных физиков, но на взгляды Фарадея смотрели как на странное заблуждение и если их и не подвергали критике и обходили в основном молчанием, то только потому, что слишком велики были заслуги Фарадея в развитии физики электрических и магнитных явлений. Нельзя указать ни одного из его современников, которому наука об электричестве и магнетизме была бы обязана таким обилием открытий первостепенной важности.
Таково было положение в физике электрических и магнитных явлений к середине XIX в. Однако это спокойствие скоро начало нарушаться. Появляются отдельные высказывания, теории, основанные на представлении о близкодействии в электрических и магнитных явлениях. Одной из таких теорий была теория Максвелла, которая в последующем произвела революционный переворот в электродинамике и в физике вообще. В чем же заключался источник этих взглядов и теорий, в том числе и теории Максвелла? Во-первых, конечно, идеи Фарадея хотя и не принимались большинством физиков, тем не менее играли революционизирующую роль. Но дело не только в этих идеях. Для их постепенного принятия нужна была соответствующая почва, объективные причины для распространения и развития идей близкодействия. Этими объективными причинами были сами характерные особенности развития физики в первой половине и в середине XIX в. Как было показано, общая тенденция развития физики и представления о физических процессах вообще заключалась в возрождении ряда картезианских идей в новой форме (на более высоком уровне). Это были идеи, которые приводили к стремлению объяснить физические явления движением различных материальных объектов. В этом смысле картезианские идеи возродились в оптике, где возникла волновая теория света, основанная на представлении о волновом движении эфира, которая заменила ньютоновскую оптику. Картезианские идеи возродились и в теории теплоты. Возникла и начала развиваться кинетическая теория тепла, рассматривающая теплоту как движение материальных частиц, из которых построено обычное вещество. Развитие механики сплошных сред в первой половине XIX в. также способствовало возрождению и распространению картезианских идей. Во всяком случае, оптика и теория теплоты — два крупных раздела физики — отошли от ньютонианских и перешли на картезианские позиции. Только теория электрических и магнитных явлений, и, конечно, теория тяготения продолжали следовать ньютонианским принципам. Но и в теории электрических и магнитных явлений произошли изменения, которые способствовали проникновению картезианских идей. Изменения заключались в необходимости учитывать не только положение проводников, заряженных электричеством, но и движение электрических зарядов и, более того, движение самих проводников. Таким образом, «движение» также вошло в теорию электричества и магнетизма, а магнитные явления вообще оказались не чем иным, как результатом движения электричества. Все это, конечно, не гармонировало с ньютонианскими представлениями. И хотя на первых порах открытия в электродинамике и получали ньютонианское толкование, тем не менее они вступали в конфликт с общими представлениями ньютонианской физики и концепции невесомых. Все это не могло не наталкивать ученых на попытки пересмотра основных взглядов на электрические и магнитные явления. С середины XIX в. у некоторых учёных (помимо Фарадея) появляются сомнения в правильности основных принципов, на которых строилась физика этих явлений. Так, например, Гаусс в письме к Веберу еще в 1845 г. писал, что он «... рассматривал как подлинный ключ электродинамики, а именно, вы» ведение силы, действующей между движущимися электрическими частицами, рассматривая эту силу не в качестве мгновенного действия на расстоянии, ио действия, распространяющегося во времени таким же образом, как распространяется свет»1. Позже (1858) ученик Гаусса Риман представил для опубликования (но затем взял обратно) работу «По поводу электродинамики». В этой работе Риман опирался на идею, что между электрическими и магнитными явлениями, с одной стороны, и явлениями распространения света и тепла — с другой, существует тесная связь. «Я установил, — писал он, — что электродинамические действия гальванических токов могут быть объяснены, если исходить из допущения, что действие электрической массы на другие совершается не мгновенно, а распространяется по направлению к ним с постоянной скоростью (в пределах возможных ошибок наблюдений равной скорости света)»2. Руководствуясь этой идеей, Римаи изменил уравнение Пуассона для потенциала, дополнив его членом, зависящим от времени, и таким образом получил уравнение для запаздывающих потенциалов, решение которого приводит к выводу о конечности распространения электрического действия. Эта работа была опубликована только после его смерти. Помимо отмеченных выше обстоятельств, толкавших ученых на пересмотр основных положений физики электрических и магнитных явлений, было еще одно обстоятельство, которое сыграло существенную роль в развитии работ Максвелла. По мере развития волновой оптики, теории теплоты и теории упругости создавался их математический аппарат. Это аппарат дифференциальных уравнений в частных производных. Уравнения описывали распределение и распространение в пространстве какой-либо физической величины, будь то световое возмущение, температура или упругие возмущения и потоки этих величин в пространстве. Следовательно, эти уравнения были пригодны для описания явлений на основе принципа близкодействия. Но, с другой стороны, уравнения для электрического потенциала являлись также дифференциальными уравнениями в частных производных. В них электрический потенциал рассматривался как функция точек пространства. Правда, использование потенциала как функции точки рассматривали как математический прием, тем не менее использовали и уравнение Лапласа и определяли выражение для потенциала как функции точек пространства. Таким образом, хотя теория потенциала основывалась на принципе дальнодействия, а теория теплопроводности — на принципе близкодействия, тем не менее и в той и в другой теории использовали дифференциальные уравнения в частных производных. Более того, некоторые уравнения для электрического потенциала и уравнения, например, в теории теплопроводности были совершенно идентичны. Это обстоятельство не могло остаться незамеченным. В. Томсон еще в 1842 г. отметил математическую аналогию между задачей распределения электрического заряда на проводниках и задачей распространения теплоты в среде. Он подчеркнул, что эквипотенциальные поверхности соответствуют в данных задачах поверхностям равной температуры, а электрический заряд — источнику теплоты. В 1846 г. Томсон установил наличие математической аналогии между задачей распределения электрического заряда и задачей распределения натяжений в упругой среде. Продолжая исследования в этом направлении, Томсон рассмотрел различные аналогии между электромагнитными явлениями, с одной стороны, и механическими и тепловыми — с другой. Он высказал мысль, что эти аналогии, возможно, не являются чисто формальными математическими аналогиями. В 1856 г. он писал: «Объяснение всех явлений электромагнитного притяжения или отталкивания, или электромагнитной индукции можно видеть для простоты в инерции или в давлении материи, которая является теплотой. Является ли эта материя электричеством или нет, является ли она непрерывной жидкостью (флюидом), заключенной между молекулами, или сама образовалась из молекул; является ли вся материя непрерывной и молекулы образованы конечными вихрями или другими движениями соприкасающихся частей тела. Это решить невозможно с помощью спекуляций при настоящем состоянии науки»3. На аналогию между гидродинамическими и электрическими явлениями указал также в 1858 г. Гельмгольц в работе, посвященной гидродинамике. Так, он отметил аналогию между магнитными силовыми линиями электрического тока и линиями тока в жидкости для случая вихревого течения. При этом направление «магнитной силы» соответствует направлению скорости движения жидкости, а электрический ток соответствует вихревой нити и т. д. Обратимся теперь к исследованиям Максвелла. Еще совсем молодым он занялся исследованием электромагнитных явлений. В 1854 г. он окончил Кембриджский университет и был оставлен при нем для подготовки к профессорскому званию. В Кембридже Максвелл пробыл два года. В это время он и начал свои исследования по электричеству и магнетизму. Его первая работа «О фарадеевских силовых линиях» была опубликована в 1855—1856 гг. На взгляды Максвелла, относящиеся к электрическим и магнитным явлениям, решающее влияние оказали работы Фарадея и В. Томсона. Максвелл впоследствии писал: «... прежде чем начать изучение электричества, я решил не читать никаких математических работ по этому предмету до окончательного прочтения мною «Экспериментальных исследований в области электричества» Фарадея»4. Изучив работы Фарадея, Максвелл понял, что для торжества и дальнейшего развития этих идей необходимо переложить их на строгий математический язык. Ведь к тому времени уже существовали количественные теории электрических и магнитных явлений, развитые Кулоном, Пуассоном, Грином, Ампером, Нейманом и др. Законы различных электрических и магнитных явлений, установленные этими учеными, не вызывали возражений. С другой стороны, построенная Фарадеем общая концепция электрических и магнитных явлений не была математически оформлена, и заранее нельзя было утверждать о такой возможности. Можно ли, основываясь на представлениях Фарадея, построить такую же строгую математическую теорию, получить уравнения, выражающие закон Кулона, закон Ампера и т. д.? Максвелл и поставил перед собой задачу перевести идеи и взгляды Фарадея на математический язык, или, говоря другими словами, интерпретировать известные законы электрических и магнитных явлений с точки зрения взглядов Фарадея. Первым шагом в решении этой задачи и послужила работа Максвелла «О фарадеевских силовых линиях». Максвелл также отмечал влияние В. Томсона на направление своих работ. Так, о работе Томсона, указанной выше, он писал: «Эта работа впервые вводила в математическую науку идею о том, что электрическое действие передается посредством непрерывной среды, идею, которая хотя и была провозглашена Фарадеем и применялась им как ведущая в его исследованиях, тем не менее никогда не была оценена другими людьми науки и рассматривалась математиками как неспособная быть согласованной с законами электрического действия, установленных Кулоном и развитых Пуассоном»5. В качестве основного метода для построения математической теории электромагнитных явлений, в основе которой лежали бы физические идеи Фарадея, Максвелл использовал метод аналогий, мысль о применении которого также заимствована у В. Томсона. Метод аналогий, по Максвеллу, заключается в том, чтобы исследователь на каждом шагу основывался на ясных физических представлениях, заимствованных из какой-либо теории и одновременно не связывал себя с этой теорией полностью. Возможность применения этого метода для развития теории Максвелл видел в существовании аналогий между различными физическими явлениями. Эти аналогии заключались в большем или меньшем сходстве различных физических явлений, имеющих неодинаковую природу. При этом сходство может быть более или менее сильным. Так, например, существует аналогия между распространением луча света и движением материальной частицы. Но это сходство распространяется только на явления геометрической оптики. Более полная аналогия существует между распространением света и распространением колебаний в упругой среде. Она идет гораздо дальше, чем первая, хотя также имеет границы применимости, переходя которые можно прийти к неверным результатам. Используя метод аналогий, Максвелл в данной работе интерпретирует основные положения электростатики с точки зрения представлений о силовых линиях. Он строит модель постоянного электрического поля. В качестве такой модели Максвелл рассматривает пространство, заполненное потоками некоторой жидкости. Это жидкость особого рода. Она несжимаема, безынерционна и течет в сопротивляющейся среде, так что сопротивление среды ее течению пропорционально скорости движения жидкости. Эта жидкость воображаемая, подчеркивает Максвелл. «Субстанции, о которой здесь идет речь,— пишет он,— не должно приписывать ни одного свойства действительных жидкостей, кроме способности к движению и сопротивлению сжатию. На эту субстанцию не следует смотреть так же как на гипотетическую жидкость в смысле, который допускался старыми теориями для объяснения явления»6. Все пространство, заполненное текущей жидкостью, можно разбить на трубки тока и при этом выбрать такие, что через сечение каждой из них в любом месте за единицу времени будет протекать единица объема жидкости. Эти трубки можно назвать единичными трубками. Далее так как течение происходит в сопротивляющейся среде, то не могут существовать замкнутые трубки тока, и, следовательно, каждая из них должна иметь начало (источник) и конец (сток). Такая модель электрического поля наглядно представляет идею Фарадея о силовых линиях. Действительно, если источник и стоки представляют собой электрические заряды, то единичные трубки тока соответствуют силовым линиям. Далее, такая модель дает возможность получить математические соотношения между величинами, характеризующими течение жидкости, которые оказываются аналогичными соотношениям, полученным в электростатике. Так, если обозначить скорость жидкости через ѵ, давление внутри нее — через р, мощность источников или стоков — через S, коэффициент сопротивления среды — через k, то между этими величинами имеют место соотношения, аналогичные существующим в электростатике между соответствующими величинами. Нужно только при этом привести в соответствие давление р и значение электрического потенциала7 φ, значение силы сопротивления среды движению жидкости kv и величину «электрической силы», т. е. напряженность электрического поля Е, значение Sk/4π и величину заряда е и т. д. Действительно, соотношение для жидкости — δp/δx = kvx, полученное Максвеллом, аналогично известному соотношению в электростатике - δφ/δx = Ex соотношение 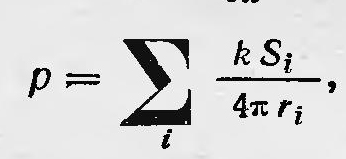
где сумма берется по всем источникам мощности S1 аналогично выражению для потенциала точечных электрических зарядов 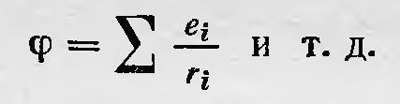
Останавливаясь на модели силовых линий как трубок тока в воображаемой жидкости, Максвелл рассматривает поляризацию диэлектриков и электропроводность. Затем он переходит к рассмотрению магнитных явлений. Для случая постоянных магнитов магнитное поле вне их наглядно изображается, как и электрическое поле электрических зарядов. Внутри же магнита каждый 'элементарный магнит Максвелл рассматривает как исток и сток воображаемой жидкости. Таким образом, построенная Максвеллом модель электрического и магнитного поля дает возможность выразить представления Фарадея на математическом языке и представть известные количественные закономерности, исходя из принципа близкодействия и конкретно на основании взглядов Фарадея. Однако эта модель пока еще не может наглядно представить явление электромагнитной индукции. Для этого и подобных явлений Максвелл еще не придумал наглядную модель. Поэтому он ограничивается математической разработкой соответствующих представлений Фарадея, чему и посвящает вторую часть своей работы, т. е. продолжает переводить идеи Фарадея на математический язык, уже не используя какую-либо модель. Здесь Максвелл пользуется рядом новых понятий — величин, которые являются функциями точек пространства. Это напряженность и индукция магнитного и электрического полей, поток напряженности и поток индукции этих полей, вектор-потенциал, а также плотность электрического тока. При этом поток магнитной индукции Максвелл рассматривает как число силовых магнитных линий, пронизывающих соответствующую площадку. Все эти величины, как известно, вошли в электродинамику, только название их изменилось. В дальнейшем при изложении трудов Максвелла будет использован современный язык формул, т. е. современные обозначения электрических и магнитных величин, а также применяться векторные обозначения, которыми Максвелл в данных работах не пользовался. Применяя эти величины, Максвелл формулирует ряд закономерностей электродинамики. Так, например, он получает формулу Стокса для циркуляции напряженности магнитного поля, а также формулу 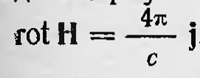 . Затем он выводит математическое выражение закона электромагнитной индукции, следуя формулировке Фарадея: . Затем он выводит математическое выражение закона электромагнитной индукции, следуя формулировке Фарадея: 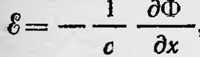 — где Φ — поток вектора магнитной индукции через соответствующий контур проводника. И наконец, получает выражение этого закона через вектор потенциал: — где Φ — поток вектора магнитной индукции через соответствующий контур проводника. И наконец, получает выражение этого закона через вектор потенциал: 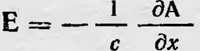 , где А — вектор-потенциал, Е — напряженность электрического поля. Величины Е, Н, Ф, А — функции точек пространства и понимаются Максвеллом с точки зрения принципа близкодействия. В последнем соотношении Максвелл видит математическое выражение идеи Фарадея об электротоническом состоянии, поэтому он называет координаты вектора А электротоническими функциями. , где А — вектор-потенциал, Е — напряженность электрического поля. Величины Е, Н, Ф, А — функции точек пространства и понимаются Максвеллом с точки зрения принципа близкодействия. В последнем соотношении Максвелл видит математическое выражение идеи Фарадея об электротоническом состоянии, поэтому он называет координаты вектора А электротоническими функциями.
Таким образом, Максвелл выполнил поставленную перед собой задачу. Он перевел идеи Фарадея на математический язык, интерпретировал известные законы электродинамики с точки зрения принципа близкодействия, использовав представления Фарадея о силовых линиях. Но пока Максвелл еще не пришел к новым фундаментальным результатам. Они появляются впервые в следующей работе Максвелла «О физических силовых линиях». Здесь впервые приведены уравнения Максвелла для электромагнитного поля. Максвелл вновь пользуется методом аналогии и строит модель электромагнитного поля, т. е. модель, которая охватывает и электромагнитные явления, а не только представляет постоянное электрическое и магнитное поля. Максвелл опять рассматривает пространство, заполненное воображаемой жидкостью. В этой жидкости образуются вихревые трубки, различно расположенные в пространстве и имеющие различную скорость движения жидкости на поверхности этих вихрей. В результате наличия таких вихревых трубок давление в жидкости в разных точках неодинаково и даже отличается в различных направлениях, т. е. среда обладает определенного рода анизотропией. Предположим, теперь, что в этой жидкости в любой точке можно выбрать малый объем, содержащий вихревые трубки, такой, что внутри него направление осей этих трубок и скорости вращения жидкости примерно одинаковы. Такой элемент объема характеризуется направлением осей вихрей, скоростью жидкости ѵ на их окружности, а также плотностью жидкости р. 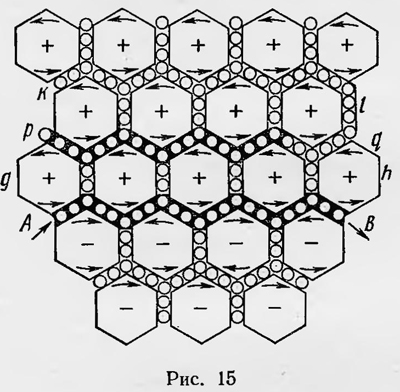
Среда, являясь анизотропной в отношении давления внутри нее, ведет себя подобно магнитному полю, если поставить в соответствие напряженности магнитного поля Н скорость жидкости на окружности вихрей ѵ, а плотности жидкости — величину магнитной проницаемости ц. Произведение же рѵ соответствует магнитной индукции В = =ηН. Это и показывает Максвелл, применяя гидродинамические расчеты к среде, состоящей из вихрей, и рассматривая эти вихри как магнитные силовые линии. При этом он получает, что плотность энергии вихрей соответствует плотности энергии магнитного поля, равной 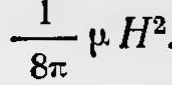 . .
Для того чтобы ввести в рассмотрение электрические и электромагнитные явления, Максвелл дополняет свою модель. Он полагает, что вихри, представляющие магнитные силовые линии, хотя и сплошь заполняют пространство, но так, что между соседними вихрями имеются слои малых частиц — шариков. Эти шарики, соприкасаясь с периферией вихрей, приводятся последними в движение подобно «холостым колесикам» между двумя большими колесами в каком-либо механизме без скольжения и трения. На рисунке, взятом из работы Максвелла, представлен элемент придуманной им среды, который поясняет ее структуру (рис. 15). Большие шестиугольники изображают поперечные сечения вихрей, а мелкие кружочки, разделяющие их, — слои частиц, являющиеся «холостыми колесиками». Если вихревые трубки представляют собой магнитные силовые линии, то маленькие шарики являются электрическими частицами. Под влиянием сил, действующих на эти частицы, они могут передвигаться (если среда является проводником) — образуется электрический ток. В случае непроводящей среды частицы могут смещаться на некоторое расстояние, причем это смещение пропорционально действующей силе. Это смещение электрических частиц и есть ток смещения. Поступательное и вращательное движения электрических частиц приводят во вращение соприкасающиеся с ними вихревые трубки или изменяют скорость их вращения. С другой стороны, вихри, вращаясь, приводят в движение соприкасающиеся с ними частицы. Они могут сообщить им как вращательное, так и поступательное движение. С помощью такой модели можно наглядно представить электромагнитные явления и, что наиболее интересно, прийти к выводу о существовании неизвестных пока явлений, а именно к выводу о существовании распространяющихся электромагнитных возмущений в пространстве. Пусть некоторый слой электрических частиц AB приходит в движение слева направо под действием некоторой силы. Это означает, что в самом этом слое действует электродвижущая сила, которая, вызывает электрический ток. В результате движения частиц в слое AB в близлежащем слое вихрей gh вихри начнут вращаться, так же как и в слое вихрей, расположенном с другой стороны от слоя частиц AB. Таким образом, вокруг тока возникает магнитное поле. С вихрями слоя gh сцеплены электрические частицы слоя pq, поэтому на них начнет действовать сила и возникнет электрическое поле. Эта сила, если частицы находятся в проводнике, вызывает их поступательное движение и в слое возникает электрический ток. Если же эти частицы находятся в диэлектрике, то они не могут двигаться. Но они могут смещаться из положения равновесия на некоторое расстояние. Они как бы «привязаны пружинками» к положению равновесия. В этом случае ток проводимости не возникает, но возникает ток смещения. Одновременно движение частиц в слое pq вызывает вращение вихрей в вихревом слое kl и, когда скорость этого вращения станет равна скорости вращения в первом вихревом слое AB, поступательное движение или смещение частиц прекратится. Так постепенно с течением времени возмущение, вызванное движением электрических частиц в первом слое AB, передается все более и более удаленным слоям. Если на пути попадаются проводники, то в них возникают кратковременные токи индукции. В конце концов движение электрических частиц во всем пространстве вызванное появлением тока в слое AB, прекратится и вокруг этого тока установится постоянное магнитное поле. Если теперь электродвижущая сила в слое АВ перестанет действовать, поступательное движение части в нем также постепенно прекратится. Это приведет и к прекращению вращательного движения в ближайшем вихревом слое pq, что вызывает кратковременные движения частиц в слое gh и т. д. Таким образом, и при прекращении тока в слое AB возникнут кратковременные токи индукции в окружающих слоях электрических частиц или кратковременные токи смещения. Придуманную модель электромагнитных явлений Максвелл подвергает математическому анализу. Он получает уравнения электромагнитного поля. Если в каком-либо элементе объема изменяется скорость ѵ вращения вихревых трубок, соответствующих, по Максвеллу, напряженности магнитного поля Н, то на единицу количества электрических частиц действует сила, которая по Максвеллу, есть напряженность электрического поля. Расчет Максвелла показывает, что между этими величинами должно быть соотношение 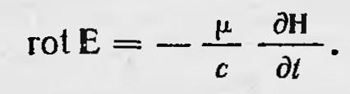
Это одно из основных уравнений электромагнитного поля. Получив уравнение, Максвелл преобразует его, вводя вектор потенциала А. В этом случае уравнение имеет вид 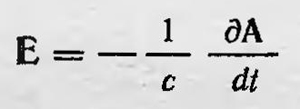
и Максвелл опять-таки истолковывает его как математическое выражение идеи Фарадея об электротоническом состоянии. Для получения второго основного уравнения нужно учесть, что образование вихревых трубок в воображаемой среде происходит не только в результате движения электрических частиц, но и под действием их смещения. Другими словами, не только электрический ток возбуждает вокруг себя магнитное поле, оно возбуждается также и током смещения. Плотность тока частиц пропорциональна количеству электрических частиц, проходящих через единичную площадку за единицу времени, а значит и скорости движения частиц. Это относится и к току смещения. Следовательно, плотность тока смещения должна быть пропорциональна Δx/Δt, где δx — смещение электрических частиц из положения равновесия в случае диэлектрика. Однако на частицы при их смещении действует упругая сила, поэтому Ах должно быть пропорционально Е, т. е. силе, действующей на единицу количества частиц, под действием которой происходит это смещение, т. е. напряженности электрического поля. Итак, плотность тока смещения определяется величиной δE/'δt и равна 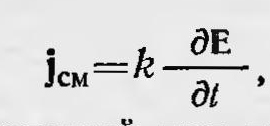
где k — коэффициент, постоянный для данной среды и определяемый ее свойствами. Значит, общая плотность тока, вызывающая магнитное поле, равна 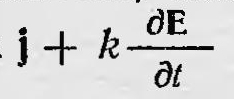 и между значением общего тока и напряженности магнитного поля, вызванного общим током, имеет место соотношение и между значением общего тока и напряженности магнитного поля, вызванного общим током, имеет место соотношение
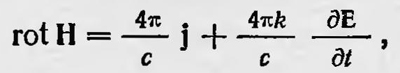
или (в современных обозначениях) 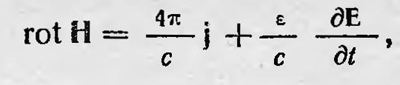
а это и есть второе основное уравнение электромагнитного поля. В рассматриваемой работе Максвелл впервые касается вопроса связи между оптическими и электромагнитными явлениями, но еще определенно не утверждает, что распространяющиеся электромагнитные возмущения и есть свет. Максвелл ограничивается только выводом, что в придуманной им среде могут распространяться поперечные волны и скорость их распространения равна скорости света. Полагая, как обычно, что скорость распространения поперечных колебаний в сплошной среде определяется формулой ѵ = √k/ρ где k — модуль сдвига, ρ — плотность среды, он выражает их отношение через магнитную и диэлектрическую проницаемость и получает, что скорость света в воздухе должна быть равна отношению количества электричества, выраженного в электростатических единицах (в системе СГСЕ), к тому же количеству электричества, выраженному в магнитных единицах (в системе СГСМ). Эго отношение, как показали измерения Вебера и Кольрауша, проделанные ими в 1857 г., равно скорости света. В связи с этим результатом Максвелл приходит к заключению: «... мы едва ли можем отказаться от вывода, что свет состоит из поперечных колебаний той же самой среды, которая является причиной электрических и магнитных явлений»8. Следующая работа Максвелла «Динамическая теория электромагнитного поля» была опубликована в 1864 г. Уже в своих предыдущих работах Максвелл пользуется понятием поля9. В этой же работе он дает этому понятию определение: «... электромагнитное поле — это та часть пространства, которая содержит в себфі окружает тела, находящиеся в электрическом или магнитном состоянии»10. Максвелл уже не строит конкретных моделей электрических и магнитных явлений. Он только постулирует, что эти явления должны вызываться действиями, происходящими в среде, окружающей тела и находящейся в «электрическом и магнитном состоянии». Этой средой, но Максвеллу, является эфир, который заполняет все пространство и пронизывает все весомые тела. Основной гипотезой, на которую опирается Максвелл в этой работе при выводе уравнений электромагнитного поля, является гипотеза о токе смещения. Ток смещения вводится Максвеллом как «электрическое смещение» заключающееся «в противоположной электризации сторон молекулы или частицы тела, которая может сопровождаться или не сопровождаться прохождением электричества через тело»11. Возникает мысль, что Максвелл говорит только о токе смещения в веществе, но это не так. Здесь под телом понимается как обычное вещество, так и эфир, который по Максвеллу, принципиально не отличается от вещества. Ток смещения, по Максвеллу, так же как и ток проводимости, создает магнитное поле. Поэтому в правую часть уравнения, являющуюся дифференциальной формой теоремы Стокса для магнитного поля 
Вектор D — вектор электрического смещения. Таким образом, получено одно из уравнений Максвелла 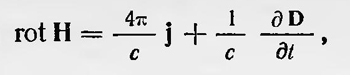
которое он называл уравнением «электрических токов». Другое основное уравнение электромагнитного поля, являющееся обобщением закона электромагнитной индукции, имеет вид 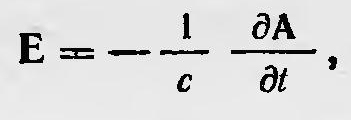
где А — вектор-потенциал. Составляющие этого вектора Максвелл называет составляющими электромагнитного количества движения. Здесь он пользуется аналогией со вторым законом Ньютона 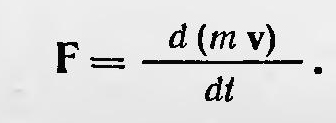
Это уравнение Максвелл никак не называет, а обобщает его на случай движущегося проводника и пишет в общем виде 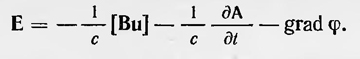
Здесь, как обычно, В — вектор магнитной индукции, u — скорость данной точки движущегося проводника, φ—электрический потенциал. Это уравнение Максвелл называет уравнением «электродвижущей силы». Смысл уравнения будет раскрыт при рассмотрении истории развития электродинамики движущихся тел. Кроме указанных выше уравнений, которые относят к главным уравнениям теории Максвелла, он рассматривает и другие уравнения, включая их в общую систему уравнений электромагнитного поля. Если все эти уравнения записать в том же порядке, что и сам Максвелл, то получим следующую систему: 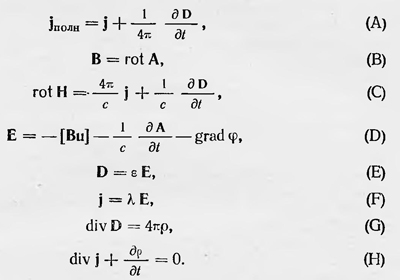
Эти уравнения несколько отличаются от системы уравнений Максвелла, которая сейчас известна. Здесь нет одного из основных уравнений электромагнитного поля — уравнения rot E = - 1/c δB/δt. Однако оно равносильно уравнениям (В) и (D) с учетом покоящихся сред. Также нет уравнения div В = 0, но оно равносильно уравнению (В). Имеются и некоторые другие отличия. Однако они носят формальный характер и не отражаются на существе дела. Отметим, что современную форму уравнения Максвелла приняли после работ Герца, Хевисайда и др. Последняя часть работы Максвелла посвящена электромагнитной теории света. Здесь уже Максвелл высказывается прямо за то, что свет есть распространяющиеся электромагнитные возмущения, электромагнитные волны. Комбинируя уравнения электромагнитного поля, Максвелл получает волновое уравнение для вектора В, откуда следует существование электромагнитных волн, распространяющихся в пространстве. Скорость их распространения определяется постоянными е и ц среды, в которой это распространение происходит, т. е. 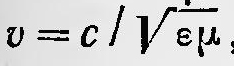 , где с — электродинамическая постоянная, равная скорости света в вакууме. , где с — электродинамическая постоянная, равная скорости света в вакууме.
Таким образом, скорость распространения электромагнитных возмущений в воздухе (для воздуха ε и η ≈ 1) равна скорости света. «Следовательно,— заключает Максвелл,— наука об электромагнетизме ведет к совершенно таким же заключениям, как и оптика в отношении направления возмущений, которые могут распространяться через поле; обе эти науки утверждают поперечность этих колебаний, и обе дают ту же самую скорость распространения»12. В 1873 г. был опубликован большой труд Максвелла «Трактат об электричестве и магнетизме», В этой фундаментальной работе он подвел итог исследованиям по электричеству и магнетизму и одновременно изложил теорию электрических и магнитных явлений на основе представлений об электромагнитном поле. В предисловии Максвелл говорил об истории своих исследований по электричеству и магнетизму, указывая, что он с самого начала поставил перед собой задачу перевести идеи Фарадея на математический язык. Максвелл сравнивает два основных направления в теории электрических и магнитных явлений: направление, основанное на представлении о действии на расстоянии, «немецком методе», и направление, в основе которого лежало представление об электромагнитном поле, — «методе Фарадея». Охарактеризовав эти два направления он подчеркивает, что в данной книге он берет на себя роль адвоката метода Фарадея и ставит перед собой задачу изложить его учение об электрических и магнитных явлениях с точки зрения теории близкодействия, положив в основу представления о поле. В «Трактате» рассмотрены все вопросы, относящиеся к электрическим и магнитным явлениям, а также ряд оптических явлений. В первом томе этого сочинения рассматриваются вопросы, относящиеся к электростатике и электрическому току. Второй том посвящен изложению магнетизма, электромагнетизма и теории электромагнитного поля. Здесь же содержатся главы, посвященные электромагнитной теории света. При изложении теории электромагнитного поля Максвелл, в основном повторяет уже полученные ранее результаты. При этом, так же как и в работе «Динамическая теория электромагнитного поля», Максвелл не строит какую-либо конкретную модель электромагнитного поля. Уравнение электромагнитного поля он получает, используя гипотезу, о токе смещения, а также применяя идею об электротоническом состоянии, т. е. гипотезу о том, что изменение магнитного поля вызывает вихревое электрическое поле. Но если Максвелл и не строит здесь конкретную механическую модель для электромагнитного поля, он тем не менее рассматривает поле как динамическую, т. е. механическую, систему. Максвелл полагает возможным применить для описания электромагнитных явлений аппарат механики Лагранжа в общем виде. При этом он вводит в качестве обобщенных координат, скоростей, количеств движения и т. д. электромагнитные величины, такие, как силу тока, электродвижущую силу, электромагнитное количество движения в точке (вектор-потенциал), считая, что эта величина выражает идею Фарадея об электротоническом состоянии и т. д. Соответствующим образом Максвелл толкует соотношения, получаемые в электродинамике (с точки зрения теории электромагнитного поля), и приходит к уравнениям для этого поля, которые имеют в основном тот же вид, что и уравнения, рассмотренные в «Динамической теории электромагнитного поля», которые приведены выше. Правда, здесь он пользуется также и векторными величинами и записывает уравнение в векторной форме. В «Трактате» гораздо более подробно Максвелл излагает электромагнитную теорию света. Он получает и исследует волновое уравнение для вектора потенциала А. Максвелл вновь приходит к выводу, что скорость света в среде определяется постоянными е и ц среды. При этом он обращает внимание на возможность проверки этого теоретического вывода на опыте, указывая, что такая проверка «является пробным камнем для электромагнитной теории света»13. Явление дисперсии света показывает, что скорость света не является постоянной величиной для всех длин волн в одной и той же среде. В связи с этим Максвелл подчеркивает, что поскольку в па определяются для постоянного поля, то и вычисленная скорость распространения электромагнитных волн должна приблизительно совпадать со скоростью света, определяемой из измерения показателя преломления для волн достаточно большой длины. В период, когда писался «Трактат», не были известны точные значения в прозрачных диэлектриков (η для них можно принять равным единице). Только для парафина значение диэлектрической проницаемости было известно достаточно точно; для парафина был известен также показатель преломления для различных длин волн. Максвелл сравнивает скорость света ѵ в парафине, определяемую из показателя преломления, со скоростью V распространения электромагнитных волн, используя значение ε. При этом он получает, что ѵ ≈ V. Таким образом, хотя достаточно точное совпадение значений этих величин и не имеет места, тем не менее полученный результат можно рассматривать как экспериментальное подтверждение электромагнитной теории света. Новым интересным вопросом, исследованным в «Трактате», является вопрос о давлении света. Рассматривая процесс распространения электромагнитных волн в веществе, Максвелл показывает, что при этом волны должны оказывать на вещество давление, определяемое величиной электромагнитной энергии, которая приходится на единицу объема, и указывает на возможность проверки этого теоретического вывода на эксперименте. Он пишет: «Плоское тело, подвергающееся действию солнечного света, будет испытывать это давление только на своей освещенной стороне и, следовательно, будет отталкиваться от той стороны, на которую падает свет. Возможно, что значительно большая энергия могла быть получена при помощи концентрированных лучей электрической лампы. Такие лучи, падая на тонкий металлический диск, весьма чувствительным образом подвешенный в вакууме, возможно, произвели бы могущий быть наблюдаемым механический эффект»14. 1Максвелл Дж. К. Избранные сочинения по теории электромагнитного поля. М., Гостехиздат, 1952, с. 628. 2Риман Б. Сочинения. М. — Л., Гостехиздат, 1948, с. 443. 3Whittaker Е. A history of the theories of aether and electricity. London, 1951, p. 245. 4Максвелл Дж. К. Избранные сочинения по теории электромагнитлого поля, с. 348. 5Whittaker Е. A history of the theories of aether and electricity, p. 241. 6Максвелл Дж. К. Избранные сочинения по теории электромагнитного поля, с. 18. 7Электрические и магнитные величины даны в современных обозначениях» 8и Максвелл Дж. К. Избранные сочинения по теории электромагнитного поля, с. 175. 9Понятие поля (feld) уже использовал Фарадей. См., например: Фарадей М. Экспериментальные исследования по электричеству. Т. 3« М. — Л., Изд-во АН СССР, 1959, с. 277. 10Максвелл Дж. К. Избранные сочинения по теории электромагнитного поля, с. 253. 11Максвелл Дж. К. Избранные сочинения по теории электромагнитного поля, с. 289. 12Максвелл Дж. К. Избранные сочинения по теории электромагнитного поля, с. 323. 13Максвелл Дж. К. Избранные сочинения по теории электромагнитного поля, с. 556. 14Там же 563. |
загрузка...
