§ 38. Развитие теории светового эфира
|
Как уже отмечалось, в самом начале волновая теория света была связана с представлением об эфире как а некой тонкой жидкости, в которой существуют продольные волны, подобно тому, как в воздухе имеют место звуковые волны. Затем было установлено, что в отличие от звуковых волн световые волны являются поперечными. Возникла проблема построения теории эфира, которая могла бы объяснить существование поперечных волн в этой среде. Эта проблема с развитием волновой оптики становится все актуальней и все более и более трудной. Усилия многих исследователей, работавших над ее решением, оказались тщетными. Однако сами исследования в этом направлении способствовали развитию механики сплошных сред, которая начала развиваться в 20-х годах XIX в. Многие исследования, имевшие существенное значение для развития этой области наук, проводили с целью построения теории светового эфира и объяснения на ее основе установленных оптических закономерностей.
Первый набросок теории светового эфира дал сам Френель. Вынашивая идею о поперечности световых волн, он понимал, что она противоречит обычным взглядам на свойства упругих сред. Он писал: «Что касается гипотезы о природе световых колебаний, то ее, с первого взгляда, гораздо труднее принять, так как не легко понять, каким образом в жидкости могут бесконечно распространяться поперечные колебания. Тем не менее, если факты, которые делают столь вероятной волновую систему и доставляют столько возражений против системы эмиссии, заставляют нас признать этот характер световых колебаний, то более надежно основываться здесь на опыте, нежели на слишком, к сожалению, несовершенных понятиях, которые нам до сих пор дали вычисления геометров относительно колебаний упругих жидкостей»1. Несовершенство представлений «геометров» заключается, по Френелю, в предположении, что в эфире возможны только упругие силы, возникающие при сжатии или растяжении, тогда как эфиру нужно приписать способность сопротивляться изменению формы. Френель считал, что эфир состоит из частиц, между которыми действуют силы притяжения и отталкивания, и что в таком эфире сила упругости должна возникать не только при сжатии и растяжении, но и в результате сдвига одних слоев эфира относительно других, а в таком случае в нем должны распространяться не только продольные, но и поперечные волны. Но так как продольных волн в эфире не существует, то сопротивление эфира сжатию несравненно больше, нежели сопротивление небольшим смещениям его слоев вдоль их плоскостей. С помощью этой гипотезы, по мнению Френеля, и можно понять, почему частицы эфира обладают заметными колебаниями лишь параллельно поверхности световых волн. Соображения Френеля оказались верными в том смысле, что в упругой среде действительно могут существовать не только продольные, но и поперечные волны. Впервые вопрос о распространении колебаний в такой среде теоретически исследовал в 1821 г. французский ученый Навье, опубликовавший эти исследования в 1827 г. Навье предложил следующую модель упругой среды. Упругая среда, по его мнению, состоит из атомов — частиц, между которыми действуют центральные силы. Навье получил уравнение распространения возмущений в такой среде. Если r — смещение частицы из положения равновесия в точке с координатами х, у, z, a ρ — плотность среды, то уравнение Навье в современной форме имеет вид: 
где k — постоянная, характеризующая упругие свойства данной среды. Несколько позже подобной проблемой занялся французский математик Огюстен Коши (1789—1857), который развил общую теорию распространения возмущений в упругой, но уже сплошной среде (1828). Он рассмотрел напряжения, возникающие в каждой точке упругого тела при малых деформациях; установил, обобщив закон Гука, соотношения между напряжениями и деформациями и вывел ряд основных положений теории упругости. Коши получил общее уравнение распространения возмущений в изотропной упругой сплошной среде: 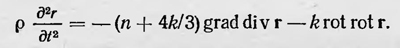
Это уравнение отличается от уравнения Навье двумя константами. При этом постоянная n — модуль Сжатия, k — модуль кручения. Исследование уравнений распространения возмущений в упругой среде показало, что в ней могут распространяться две волны: продольная со скоростью 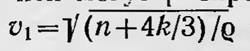 и поперечная, скорость которой и поперечная, скорость которой 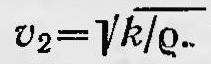 . Таким образом, строгая математическая теория распространения возмущений в упругой среде подтвердила простые соображения Френеля о возможности поперечных волн в такой среде. Однако эта же теория указала и на существование в ней продольных волн. Но в эфире продольных оптических волн никто не наблюдал. И если их действительно не существует, то эфир должен отличаться от обычной упругой среды. Чем же отличается эфир от обычной упругой среды? По этому вопросу существовало много гипотез. Одной из них была гипотеза Френеля, которая сводилась к тому, что, как говорилось выше, эфир обладает бесконечно большим модулем сжатия, т. е. является абсолютно несжимаемой средой. В такой среде продольных волн не существует. А так как модуль сдвига для эфира остается конечным, то поперечные волны в нем не существуют. Они и являются световыми волнами, распространяющимися со скоростью . Таким образом, строгая математическая теория распространения возмущений в упругой среде подтвердила простые соображения Френеля о возможности поперечных волн в такой среде. Однако эта же теория указала и на существование в ней продольных волн. Но в эфире продольных оптических волн никто не наблюдал. И если их действительно не существует, то эфир должен отличаться от обычной упругой среды. Чем же отличается эфир от обычной упругой среды? По этому вопросу существовало много гипотез. Одной из них была гипотеза Френеля, которая сводилась к тому, что, как говорилось выше, эфир обладает бесконечно большим модулем сжатия, т. е. является абсолютно несжимаемой средой. В такой среде продольных волн не существует. А так как модуль сдвига для эфира остается конечным, то поперечные волны в нем не существуют. Они и являются световыми волнами, распространяющимися со скоростью 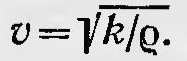 . Конечно, гипотеза Френеля, согласно которой эфир представлялся как несжимаемая среда, подобная твердому (и даже очень твердому) телу, поскольку скорость поперечных волн в нем (т. е. скорость света) очень велика, представлялась по меньшей мере странной. Как же в такой среде, заполняющей все пространство, могут без всякого сопротивления двигаться небесные тела и обычные макроскопические предметы? Ведь на самом деле эфир не оказывает такому движению никакого сопротивления. . Конечно, гипотеза Френеля, согласно которой эфир представлялся как несжимаемая среда, подобная твердому (и даже очень твердому) телу, поскольку скорость поперечных волн в нем (т. е. скорость света) очень велика, представлялась по меньшей мере странной. Как же в такой среде, заполняющей все пространство, могут без всякого сопротивления двигаться небесные тела и обычные макроскопические предметы? Ведь на самом деле эфир не оказывает такому движению никакого сопротивления.
Ответить на этот вопрос попытался в 1845 г. английский ученый Стокс (1819—1903). Он считал, что эфир подобен смоле, которая обладает свойством твердого тела в случае быстро меняющихся деформаций и пластична, подобно жидкости, при медленно меняющихся деформациях. Эфир, по мнению Стокса, в первом случае является твердым телом и в нем распространяются поперечные волны. Для медленных же деформаций, в случае малых скоростей движущихся в нем тел, он ведет себя как жидкая среда, в которой эти тела могут свободно передвигаться, не испытывая сопротивления. Теория эфира, однако, должна была не только показать, что в нем могут распространяться поперечные волны и отсутствовать продольные. Она должна была объяснить ряд световых явлений и их закономерностей. Во-первых, перед ней стояла задача объяснения закономерностей, имеющих место при отражении и преломлении света на границе двух сред. Этот вопрос впервые исследовал Френель, который получил формулы, известные под названием формул Френеля. При этом он исходил как раз из гипотезы, о несжимаемом эфире. Для решения поставленной задачи Френелю пришлось принять ряд дополненных гипотез. Во-первых Френель предположил, что плоскость колебаний световых волн перпендикулярна плоскости поляризации. Во-вторых, решая вопрос о том, чем отличается эфир в средах с различным показателем преломления [ведь если скорость света (скорость поперечных волн) равна 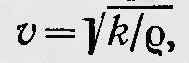 , то эфир должен различаться в разных средах либо плотностью, либо упругостью, либо и тем и другим], Френель принял гипотезу о том, что в разных средах плотность эфира различна, тогда как упругость остается без изменения. Таким образом, по Френелю, для двух тел, показатели преломления которых соответственно равны n1 и n2, имеет место соотношение , то эфир должен различаться в разных средах либо плотностью, либо упругостью, либо и тем и другим], Френель принял гипотезу о том, что в разных средах плотность эфира различна, тогда как упругость остается без изменения. Таким образом, по Френелю, для двух тел, показатели преломления которых соответственно равны n1 и n2, имеет место соотношение
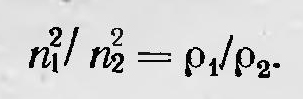
Выводя искомые формулы, Френель основывался на законе живых сил и предположении^ непрерывности тангенциальных составляющих смещения в эфире на границе двух сред. Рассмотрим падающий, преломленный и отраженный пучки света (рис. 47). Пусть i — угол падения, а г — угол преломления. Энергия, переносимая через поперечные сечения световых пучков за единицу времени, в падающем, отраженном и преломленном пучках соответственно пропорциональна ABv1ρ1f2, acv1ρ1g2, abv2ρ2h2, где v1 и v2— соответственно скорость света в первой и во второй средах; ρ1 и ρ2— плотность эфира в первой и второй средах; f, g,h — соответственно амплитуда световой волны в падающем, отраженном и преломленном пучках. 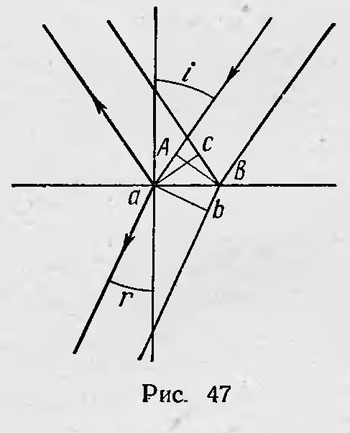
Согласно закону сохранения живых сил, ABv1ρ1f2=acv1ρ1g2+abv2ρ2h2. Для случая, когда колебания в падающем свете перпендикулярны плоскости падения, предположение о равенстве тангенциальных слагающих дает условие f = g + h. Кроме того, имеем АВ=аВ cos i, ас=аВ cos i, ab=аВ cos r. Учитывая также, что n12/n22=ρ1/ρ2=sin2r/sin2i=v22/v12, и производя простой расчет, получаем f/g = — sin (i — r)/sin (i + r). Это и есть одна из известных формул Френеля, устанавливающая отношение амплитуды падающего света к амплитуде отраженной световой волны. Поступая аналогично, Френель получает формулы для случая, когда колебания световой волны происходят в плоскости падения: f/g = tg(i—r)/tg(i + r). Успех Френеля понятен. Хотя он и исходил из представления об эфире, тем не менее принял правильные гипотезы, которые не зависели от этой теории. В этом вновь проявилась гениальная интуиция Френеля. Его гипотеза о сохранении энергии при прохождении светового потока через границу двух сред и гипотеза о непрерывности тангенциальной слагающей светового вектора оказались верны. Они действительны и в электромагнитной теории света. Рассуждения Френеля далеки от строгости, но это в данном случае не является недостатком. Наоборот, только это обстоятельство дало ему возможность получить правильные формулы. Если бы Френель следовал строгой теории распространения возмущения в твердом эфире, он не смог бы прийти к правильным результатам. Это показал последующий анализ. Френель не строил строгую теорию, а просто принял гипотезы, которые подсказывала ему интуиция. Этими гипотезами были: предположение о направлении световых колебаний в плоскополяризованном свете, а также гипотеза о непрерывности тангенциальной слагающей светового вектора на границе двух сред. Руководствуясь этими гипотезами и используя закон сохранения энергии, он и пришел к верным результатам. Многочисленные попытки усовершенствовать выводы Френеля на основе более строгих теорий не привели к положительным результатам. С помощью теории упругого эфира не удавалось дать аналитический вывод формул Френеля, рассматривая эфир как несжимаемую сплошную среду. Кроме теории твердого эфира возникли и другие предположения о свойствах эфира. Так, например, Коши в 1839 г., стараясь исключить продольные волны, высказал гипотезу так называемого «сжимающегося» или «лабильного» эфира. Для того чтобы избавиться от продольной волны, считал он, не обязательно полагать, что n=∞ и vпрод =∞; можно наоборот, считать, что vпрод =0. Но тог да так как 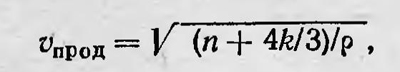
то модуль сжатия n должен быть отрицательным, т. е. эфир должен обладать отрицательным сопротивлением сжатию. Эта гипотеза приводила к хорошим результатам, однако казалась слишком странной, так как представляла эфир как неустойчивую среду. В дальнейшем В. Томсон возродил гипотезу Коши и в качестве модели сжимающегося эфира предложил рассматривать мыльную пену, удерживаемую от сжатия тем, что она прилипает к стенкам сосуда. Теорию сжимающегося (лабильного) эфира разрабатывали и некоторые ученые, в частности Гиббс, который показал, что она может приводить к положительным результатам. В 1839 г. Мак-Куллах предложил оригинальную теорию светового эфира. Он исходил из того, что эфирная среда обладает необычными свойствами, а именно упругостью только в отношении вращения, и не оказывает никакого сопротивления другим видам деформации. В эфире Мак-Куллаха потенциальная энергия деформации единицы объема выражается формулой 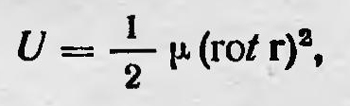
где r — смешение частицы в точке (х, у, r), а μ — коэффициент, характеризующий упругость среды. Уравнение распространения возмущений в такой среде, как показал Мак-Куллах, имеет вид 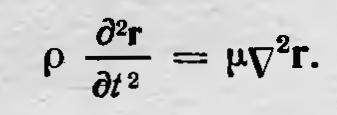
Это волновое уравнение поперечных волн, скорость распространения которых 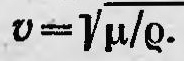 . Далее, из теории Мак-Куллаха следует, что на границе двух сред сохраняется непрерывность тангенциальных слагающих r и μ rot r. Теория Мак-Куллаха давала правильные результаты. Она приводила к граничным условиям, из которых можно получить формулы Френеля. Наконец, ее можно было распространить на анизотропные тела, получив при этом правильные результаты. . Далее, из теории Мак-Куллаха следует, что на границе двух сред сохраняется непрерывность тангенциальных слагающих r и μ rot r. Теория Мак-Куллаха давала правильные результаты. Она приводила к граничным условиям, из которых можно получить формулы Френеля. Наконец, ее можно было распространить на анизотропные тела, получив при этом правильные результаты.
На теорию Мак-Куллаха в свое время не обратили серьезного внимания и вспомнили о ней только после создания Максвеллом электромагнитной теории света. Тогда даже было показано, что ее можно интерпретировать в понятиях электромагнитной теории света Максвелла. Для эфира Мак-Куллаха В. Томсон даже придумал специальную модель. Она представляла собой систему гироскопов, соединенных специальными шарнирами, и действительно обладала свойствами эфира Мак-Куллаха. Перед теорией эфира стояли и другие трудные задачи, в частности объяснение дисперсии света. Если рассматривать эфир как сплошную среду, то нельзя объяснить это явление. Для такой среды скорость распространения возмущений не зависит от частоты. На этот вопрос впервые обратил внимание опять же Френель. Он считал возможным объяснить дисперсию света, приняв гипотезу, согласно которой эфир состоит из частиц, расстояние между которыми сравнимо или больше длины световых волн. В этом случае следует ожидать, что скорость света зависит от длины волны. Эта идея была разработана Коши, который в 30-х годах аналитически доказал, что в таком эфире скорость распространения волн действительно зависит от частоты, т. е. должна иметь место дисперсия. Коши получил формулу, известную под названием формулы Коши, выражающую зависимость скорости света от длины волны: с2=α—β(2π/λ)2+γ(π/λ)4-... Здесь λ — длина волны, α, β, γ — коэффициенты, постоянные для данной среды. Иначе к вопросу о дисперсии подошел (правда, позже) французский ученый Буссинеск. В отличие от предшественников он отказался от гипотезы, что упругость или плотность эфира зависит от вещества, в котором он находится. В 1868 г. Буссинеск высказал предположение, что эфир и внутри тел, и в вакууме имеет одну и ту же упругость и плотность. Особенности же прохождения света через тела объясняются взаимодействием световых волн, распространяющихся в эфире, с молекулами этих тел. Отправляясь от этих предположений, Буссинеск разработал теорию дисперсии, которая была шагом вперед и предвосхищала некоторые идеи возникшей позднее электронной теории, хотя и исходила еще из представления об упругом эфире. Дальнейшие шаги в развитии теории эфира относятся к периоду установления электромагнитной теории света, когда встал вопрос уже о построении не только теории светового эфира, но и теории эфира, объединяющей световые и электромагнитные явления. 1Френель О. Избранные труды по оптике, с. 397. |
загрузка...
