§ 11. Первые шаги в развитии механики

Механика как учение о движении по-настоящему начинает развиваться в работах Галилея, относящихся к концу XVI и первой половине XVII в. Первый этап ее развития завершается выходом в свет главного труда Ньютона «Математические начала натуральной философии» — первого систематического изложения классической механики. Рассмотрим, как развивалась механика доньютоновского периода. В этот период механика развивается в основном в направлении решения некоторых простейших механических задач, при решении которых формируются и развиваются основные понятия классической механики. Первые, самые простые задачи механики— задачи падения и движения тел по наклонной плоскости — были решены Галилеем. Уже упоминались исследования Галилея по механике в связи с его борьбой за признание учения Коперника. Мы говорили об открытии им закона инерции и принципа относительности. Однако следует иметь в виду, что механикой Галилей занимался, конечно, не только для оправдания учения Коперника. Другой причиной была техническая проблематика, к которой он проявлял большой интерес. Первой конкретной задачей механики, которую решил Галилей, была задача свободного падения тел.

О ней упоминалось при рассмотрении метода исследования Галилея. Исходя из предположения, что тела падают равноускоренно, Галилей теоретически выводит следствие, что в этом случае путь должен быть пропорционален квадрату времени. Затем проверяет этот вывод на эксперименте. Здесь упомянем, как из гипотезы о том, что v~t, Галилей получил, что s~t². Для этого он применил нечто вроде примитивного метода графического интегрирования — почти так же, как это делают в настоящее время в средней школе.

Галилей решает также задачу движения тела, брошенного под углом к горизонту, в случае отсутствия силы трения. При этом он опирается на закон инерции и принцип разложения движения на две составляющие: движение в горизонтальном направлении с постоянной скоростью и вертикальное движение по закону падения тел. Следуя этому принципу, Галилей приходит к правильному выводу, что траектория движения в данном случае представляет собой параболу. При этом он показал, что наибольшая дальность полета тела при равных начальных скоростях имеет место при угле бросания, равном 45°.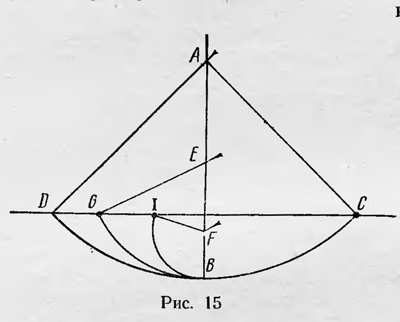

Галилей рассматривает задачу движения тела по наклонной плоскости. Основной результат, полученный им, таков: «Степени скорости, приобретаемые одним и тем же телом при движении по наклонным плоскостям, равны между собой, если высоты этих наклонных плоскостей одинаковы»¹. Для обоснования этого положения Галилей сначала обращается к опыту. Он рассматривает движение простого маятника— шарика, подвешенного на тонкой нити. Опыт показывал, что шарик при колебаниях всегда поднимается на одну и ту же высоту постепенное уменьшение амплитуды маятника объясняется сопротивлением воздуха). Этот закон выполняется и в случае, если заставить шарик двигаться по различным дугам. Пусть на пути движения нити закреплен гвоздик в положении Е или F (рис. 15). Несмотря на то что шарик маятника теперь двигается по кривой BG или BI, высота, на которую он поднимается, как показывает опыт, остается той же самой. С другой стороны, если шарик падает по кривой GB или IB, то он всегда поднимается в положение С. Отсюда, по Галилею, следует, что «момент» приобретаемый шариком при падении его по дугам DB, GB, IB будет одним и тем же, так как шарик всегда поднимается в положение С. Следовательно, падая по различным кривым, но с одной и той же высоты, шарик приобретает один и тот же «момент». Если это положение распространить на движение тела по наклонной плоскости и принять во внимание, что равным «моментам» соответствуют равные скорости, то положение Галилея подтверждается. В этом рассуждении интересным является то, что оно основано на свойстве консервативности силы тяжести или законе сохранения энергии применительно к простейшим случаям движения тела. В связи с этим приведенное рассуждение можно считать отправным пунктом, от которого начинает развиваться представление о законе сохранения энергии в механике.

Рассматривая движение тела по наклонной плоскости, Галилей делает также еще один шаг в развитии динамики. Он выдвигает идею связи движения тела с силой, вызывающей это движение. Изучая движение тела по наклонной плоскости, Галилей опять использует понятие «момента» или «импульса». При этом «импульс» используется как величина, характеризующая движение тела, и как величина, характеризующая стремление тела к движению, поэтому имеет как бы две меры. Во-первых, величина «импульса» определяется скоростью тела, поскольку при сравнении «импульсов» сравниваются пути, проходимые, телом за один и тот же промежуток времени с начала движения. Во-вторых, «импульс» измеряется силой, необходимой для того, чтобы не допустить движение тела. Галилей пишет:

«Совершенно ясно, что импульс тела к падению столь же велик, как то наименьшее сопротивление или та наименьшая сила, которая достаточна для того, чтобы воспрепятствовать падению и удержать тело»².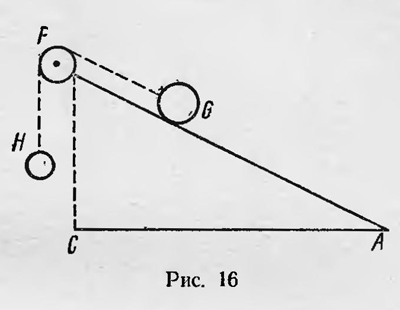

В качестве такой силы Галилей рассматривает тяжесть. Если два связанных тела (рис. 16), из которых одно (G) помещено на наклонной плоскости, а другое (Я) подвешено вертикально, находятся в равновесии, то тяжесть тела Н уравновешивается стремлением тела G двигаться по наклонной плоскости и является мерой его «импульса».

Таким образом, «импульс», по Галилею, поскольку он определяется скоростью, является характеристикой движения, его мерой, но «импульс» пропорционален приобретенной скорости, т. е. приращению скорости. Сравнивая «импульс» тела при движении его по наклонным плоскостям с различным углом наклона, Галилей сравнивает скорости, приобретенные за определенный промежуток времени. Так как Галилей рассматривает только равноускоренное движение, т. е. движение под действием постоянной силы, то промежутки времени он может брать любые и безразлично, конечные или бесконечно малые. Поэтому величина «импульса» определяется не только скоростью, но и ее приращением. Последнее обстоятельство позволяет Галилею измерять «импульс» силой, под действием которой тело приходит в движение. Таким образом, понятие «импульса» у Галилея включает и представление о действии на тело, в результате которого тело приобретает данный запас движения, данную скорость.

Понятие «импульса» или «момента» у Галилея можно рассматривать как дальнейшее развитие понятия «импетуса». Однако Галилей делает принципиально новый шаг вперед по сравнению с теорией «импетуса», используя понятие «момента» или «импульса». Хотя его понятие «импульса» расплывчато и включает зародыши понятий количества движения и силы, тем не менее в данном случае с Галилея начинается анализ движения, начинают формироваться понятия силы и изменения количества движения, т. е. основной закон механики.

Следующей задачей механики, которая была разрешена в рассматриваемый период, была задача о маятнике. Решение задачи о маятнике было непосредственно связано с практической задачей точного измерения времени. Особенно важна была эта задача для мореплавания. Необходимо было точно уметь определять местонахождение судна, а для этого требовались хорошие часы. Галилей еще в молодости пришел к заключению об изохронности колебаний маятника. При этом он ошибочно считал эту изохронность точной. Затем он установил, что период колебаний математического маятника Т где I — его длина. Галилею принадлежит идея использования маятника для устройства часов. Галилей использовал маятник для определения частоты пульса у больных. Впоследствии он создает проект часов с маятником, который не был претворен в жизнь.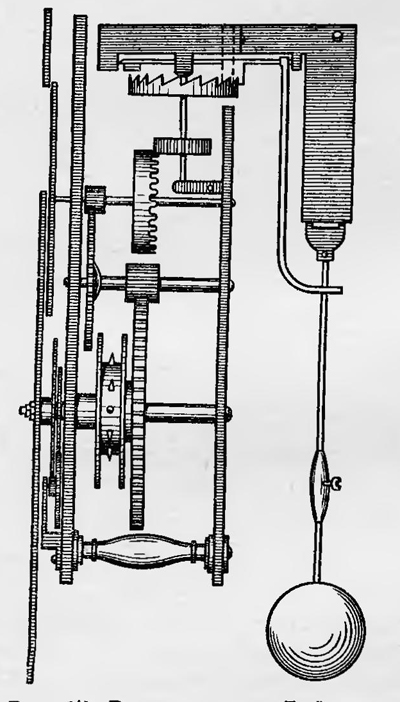

Рис. 17. Рисунок часов Гюйгенса мало чем отличалась от простейших

Часы с маятником были изобретены голландским ученым Христианом Гюйгенсом (1629—1695)—одним из выдающихся физиков, математиков и астрономов XVII в. Конструкция часов Гюйгенса (рис. 17) современных часов-«ходиков». Главное отличие состояло в том, что они не имели так называемого анкерного спуска, кроме того, маятник в них двигался так, что чечевица описывала дугу циклоиды. Гюйгенс описал устройство изобретенных им часов в брошюре, вышедшей в 1658 г., а затем в работе «Качающиеся часы, или о движении маятника», вышедшей в свет только в 1673 г. В этом сочинении он изложил также свою теорию математического и физического маятника.

Христиан Гюйгенс

Гюйгенс рассматривает свободное падение тел, движение тел по наклонной плоскости, падение тел по ряду следующих друг за другом наклонных плоскостей и падение тел по кривой поверхности, представив ее как предел множества наклонных плоскостей. Он показал, что скорость, приобретенная телом при падении, не зависит от траектории падения, а определяется только высотой, с которой упало тело. При этом Гюйгенс широко использует «энергетический» принцип, доказанный им для свободного падения: тело может подняться только на ту высоту, с которой оно упало.

Особое внимание Гюйгенс уделяет движению тела по дуге циклоиды. Для этого случая, опираясь на полученные результаты и энергетический принцип, Гюйгенс доказывает, что при движении тела по циклоиде, обращенной вершиной вниз, время спуска и подъема (т. е. время одного простого колебания) относится ко времени свободного падения по длине оси циклоиды, как дуга окружности к своему диаметру. Отсюда следует изохронность колебаний тела по циклоиде и возможность определения периода такого колебания.

Из вывода Гюйгенса следует известная формула для периода Т колебаний математического маятника: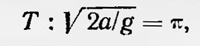

где а — ось циклоиды. Учитывая, что 2а=1, где I — радиус кривизны циклоиды, для малых колебаний математического маятника получаем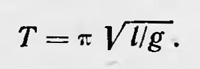

Гюйгенс исправляет ошибку Галилея, который полагал,что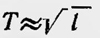

является точной зависимостью, а не приближенным выражением, справедливым только для малых колебаний. Этот вывод и послужил причиной выбора для часов маятника, чечевица которого совершает колебания по циклоиде.

В этом сочинении Гюйгенс решает и более трудную задачу о колебаниях физического маятника. Наиболее интересен основной принцип, который Гюйгенс положил в основу теории физического маятника. Он явился дальнейшим развитием представления о законе сохранения энергии в механике. Вот как сам Гюйгенс формулирует этот принцип:

«Если любое число весомых тел приходит в движение благодаря их тяжести, то общий центр тяжести этих тел не может подняться выше, чем он был в начале движения»³.

Гюйгенс делает новый шаг в развитии учения о невозможности вечного двигателя и о сохранении энергии. Комментируя указанный принцип, он подчеркивает его эвристическое значение и пишет, что с помощью этой гипотезы можно доказать много теорем механики.

«И если бы, — заключает он, — изобретатели новых машин, напрасно пытающиеся построить вечный двигатель, пользовались этой моей гипотезой, то они легко бы сами сознали свою ошибку и поняли, что такой двигатель нельзя построить механическими средствами»⁴.

Изложим кратко в современном виде основную идею вывода Гюйгенса, лежащую в основе теории физического маятника. Пусть физический маятник состоит из невесомого стержня ОА (рис. 18), на котором на расстояниях х₁, х₂, х₃,..., х_n от точки подвеса О расположены соответственно массы m₁, m₂, m₃,..., m_n. Тогда центр тяжести этих масс находится на расстоянии х = Σ(m_ix_i)/Σm_i от точки подвеса О.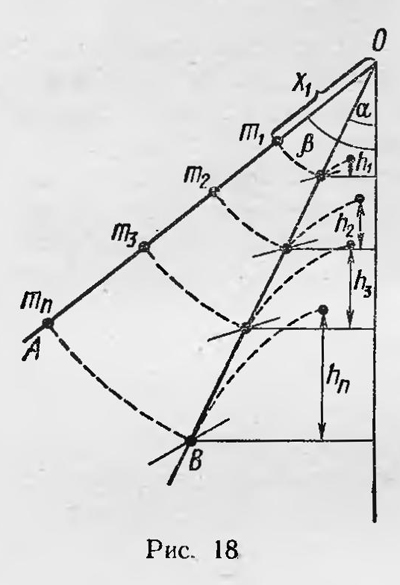

Маятник выведен из равновесия и находится в положении ОА так, что стержень образует с вертикалью угол β. Отпустим маятник и проделаем следующий мысленный эксперимент: когда стержень будет проходить положение ОБ и образует с вертикалью угол а, нарушим связь между массами и дадим им двигаться самостоятельно любым образом⁵, лишь бы они могли при этом подняться на максимально доступные им высоты h₁, h₂,..., h_n. Высоты, на которые способны подняться массы, определяются скоростями v₁, v₂, ..., v_n, которые они имели при прохождении стержнем положения ОБ, и соответственно равны h₁=v₁²2/g, h₂=v₂²2/g, ..., h_n=v_n²2/g, где g— ускорение силы тяжести.

Высота Н, на которую поднимается центр тяжести, очевидно, такова: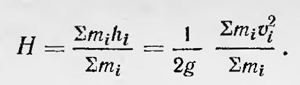

Введя угловую скорость со, это равенство можно записать в виде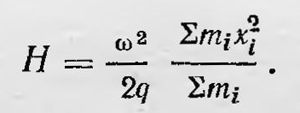

Однако, по основной гипотезе Гюйгенса, высота, на которую может подняться центр тяжести самостоятельно двигающихся масс, должна быть равна высоте, с которой до этого упал центр тяжести маятника. Последняя же равна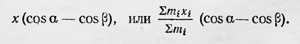

Следовательно, имеем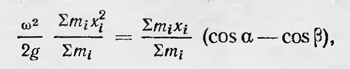

откуда для значения ω² получаем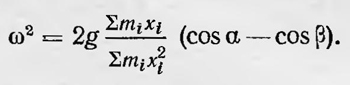

Рассмотрим теперь математический маятник O'А' длиной l (рис. 19), который начинает двигаться из положения, когда его нить образует с вертикалью тот же угол β. Определим его угловую скорость (ω¹ когда он, двигаясь к положению равновесия, проходит положение О'В' и когда его нить образует с вертикалью (как и в первом случае) угол α. Как легко видеть,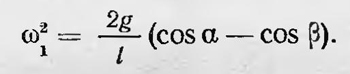

Углы α и β произвольны, поэтому математический маятник, имеющий длину, равную Σ(m_ix_i²)/Σ(m_ix_i), колеблется изохронно с физическим маятником. Таким образом, найдена так называемая приведенная длина физического маятника для рассмотренного простейшего случая. Полученный результат может быть обобщен, что и приводит к решению задачи о физическом маятнике.

В рассматриваемый период решалась задача об ударе тел, которой уже интересовался Галилей. Затем Декарт пытался установить законы удара, которые в его натурфилософии должны были играть важную роль как законы, лежащие в основе всех взаимодействий в природе. В 1666 г. Лондонское королевское общество объявило конкурс на тему об ударе тел. Было прислано три работы: английских ученых Рена и Валлиса, а также Гюйгенса. Валлис рассмотрел случай неупругого удара, Рен и Гюйгенс исследовали упругий удар. Наибольший интерес представляет работа Гюйгенса, хотя она и не была опубликована в Англии вместе с работами Валлиса и Рена; основные ее результаты были напечатаны во Франции. Полностью исследования Гюйгенса по теории удара были опубликованы только в 1703 г. Интересны методы и принципы, которые Гюйгенс использует в этом исследовании. Он начинает с утверждения, что два упругих одинаковых шара, которые движутся навстречу с одинаковыми скоростями, отскакивают друг от друга с теми же скоростями, но направленными в противоположные стороны. Это один из основных постулатов теории удара Гюйгенса.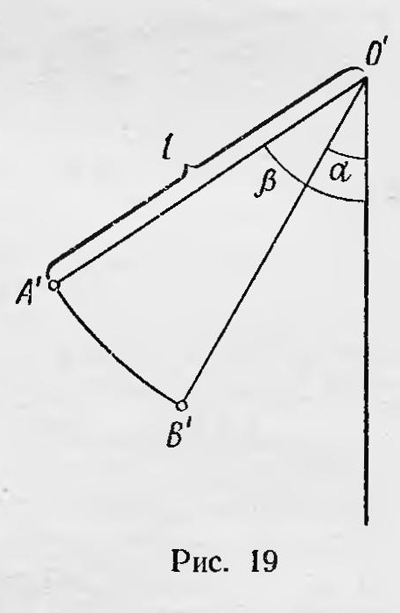

Затем Гюйгенс рассматривает центральный удар двух одинаковых шаров, имеющих разные скорости. Для решения этой задачи он привлекает принцип относительности. Представим себе, что в лодке, плывущей по реке вдоль берега с постоянной скоростью, стоит человек и держит в руках нити, на которых подвешены два одинаковых шара (рис. 20). Пусть этот человек сближает руки с одной и той же скоростью относительно лодки и производит удар шаров. Тогда, согласно принципу относительности, имеет место простейший случай удара, о котором говорилось выше. Следовательно, после удара шары отскочат с теми же скоростями, которые

они имели до удара, только изменят направление движения на обратное. Однако другую картину наблюдает человек, стоящий на берегу. Для него шары будут двигаться с разными скоростями и, как легко видеть, после удара обменяются ими. Далее Гюйгенс рассматривает удар неодинаковых шаров. Он сначала решает задачу для частного случая удара шаров, сближающихся со скоростями, обратно пропорциональными их величинам (т. е. массам). Для этого случая он доказывает, что шары после удара сохраняют свои скорости по абсолютной величине. При доказательстве этого положения Гюйгенс применяет принцип относительности и энергетический принцип, который он использовал в теории физического маятника, рассматривая соударение шаров, подвешенных на нитях.

После того как Гюйгенс рассмотрел частный случай соударения неодинаковых шаров, он вновь применяет принцип относительности. Человек в лодке производит удар шаров рассмотренным выше способом. Для наблюдателя на берегу это будет уже общий случай упругого центрального удара шаров. Теория удара шаров интересна также тем, что в ней Гюйгенс делает новые шаги в установлении законов сохранения. Во-первых, он показывает, что в формулировке Декарта закон сохранения количества движения не выполняется. Он даже доказывает, что «когда два тела соударяются, то не всегда сохраняется количество движения, бывшее в обоих до удара, но оно может уменьшаться или увеличиваться»⁶. Говоря о теории удара, Гюйгенс возражает против закона Декарта и одновременно формулирует правильный закон сохранения количества движения применительно к явлению столкновения двух тел. Он пишет:

«Количество движения, которое имеют два тела, может увеличиваться или уменьшаться при столкновении; но его величина остается постоянной в ту же сторону (в том же направлении), если мы вычтем количество движения обратного направления»⁷

Наконец, Гюйгенс доказывает теорему, являющуюся частным случаем теоремы живых сил, или закон сохранения кинетической энергии для упругого удара. Он доказывает, что «при соударении двух лет (при упругом ударе.— Б. С.) сумма произведений из их величин на квадраты их скоростей остается неизменной до и после удара»⁸. Таким образом, Гюйгенс делает новый шаг в развитии представления о сохранении энергии в механических процессах.

Следующей задачей динамики, послужившей предметом исследования в XVII в. (до Ньютона), была задача о движении материальной точки по окружности. Ее также успешно рассмотрел Гюйгенс и опубликовал полученные результаты в работе, посвященной теории маятника, о которой говорилось выше. Полностью этот вопрос был исследован в работе «О центробежной силе», опубликованной после его смерти в 1703 г. В этой работе Гюйгенс проводит очень интересные рассуждения, касающиеся вопроса установления связи между силой и ускорением. Если тело висит на нити, то нить испытывает натяжение, так как тело стремится двигаться вниз с постоянным ускорением. В случае, если тело удерживается нитью на наклонной плоскости, нить также испытывает натяжение и опять по той же причине. Но в первом случае ускорение оторвавшегося тела будет другим, нежели во втором. Соответственно различны и натяжения нити. Больше того, отношение величин ускорений пропорционально натяжению нити. Гюйгенс обобщает эти выводы и высказывает существенно новое утверждение, что ускорение должно быть Пропорционально натяжению нити в начале движения и что это положение носит общий характер и применимо не только тогда, когда тело находится под действием силы тяжести. Таким образом, Гюйгенс сделал новый шаг вперед к пониманию связи между силой и ускорением.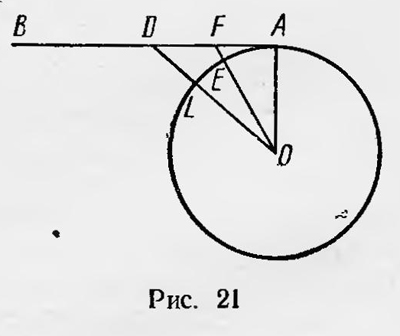

Используя приведенные соображения, Гюйгенс находит выражение для центробежной силы (силы натяжения нити). Вращающийся шарик натягивает нить вследствие того, что в каждый момент стремится двигаться прямолинейно по касательной.

Для того чтобы определить натяжение нити, нужно знать «стремление» шарика оторваться от нее, т. е. с каким ускорением по отношению к нити он стал бы двигаться, оторвавшись от нее.

Представим себе, что в некоторый момент времени t в точке А шарик оторвался от нити и стал двигаться по касательной АВ (рис. 21). Тогда в первый очень малый промежуток времени он пройдет отрезок AF, во второй — FD и т. д. Следовательно, он будет удаляться от конца нити за эти промежутки времени соответственно на расстояния EF, LD и т. д. Продолжая рассуждения, Гюйгенс определяет величину центробежной силы в зависимости от скорости вращения, радиуса круга и веса тела.

Заканчивая обзор развития механики доньютоновского периода, остановимся кратко на исследованиях Лейбница. Хотя Лейбниц и был современником Ньютона, тем не менее его механика носила характер доньютоновской механики. Готфрид Вильгельм Лейбниц (1646—1716)—немецкий философ и ученый. Ему принадлежат многие работы по философии, математике, физике и другим наукам. Не останавливаясь на его философской системе объективного идеализма, отметим лишь, что, по Лейбницу, в основе всего существующего лежит не материя, а некие неделимые субстанции — «монады», являющиеся центрами деятельных сил. Свои общие философские взгляды Лейбниц старался связать с естественнонаучными представлениями, в частности с механикой. Последнее нашло свое выражение в учении Лейбница о сохранении живой силы, которое он противопоставлял учению Декарта о сохранении количества движения в природе.

Занимаясь исследованием по механике, Лейбниц обратил внимание на трудности, связанные с пониманием закона сохранения количества движения Декарта, на критику Гюйгенсом этого закона. Он ознакомился также с результатами работ последнего о сохранении кинетической энергии при упругом ударе. Рассмотрев эти вопросы, он пришел к идее об общем законе сохранения — законе сохранения живых сил. Этот закон он противопоставил закону сохранения количества движений Декарта и расценивал его как подтверждение своей философии. В 1686 г. Лейбниц выступил в печати со статьей «Краткое доказательство примечательной ошибки Декарта и других относительно закона природы, согласно которому бог всегда сохраняет одно и то же количество движения и которым неправильно пользуются, между прочим, в механической практике». В ней, а затем в ряде других сочинений Лейбниц опровергал закон сохранения движения Декарта. Он утверждал, что в природе действует не закон сохранения количества движения, а закон сохранения живой силы, которая, как он считал, пропорциональна не скорости тела, а ее квадрату. «Сила», по Лейбницу, должна измеряться тем действием, которое она может произвести; таким действием является, например, поднятие тела вверх на определенную высоту. Но высота, на которую может подняться тело, пропорциональна не скорости, а квадрату скорости. Поэтому «сила» движущегося тела также пропорциональна квадрату его скорости.

Закон Декарта, утверждает Лейбниц, будет справедлив, если учитывать, что количество движения может иметь как положительный, так и отрицательный знак. Такой закон Лейбниц называл законом сохранения «направления» (directionis) или законом сохранения «движения вперед». Лейбниц писал:

«Кроме изложенного выше закона природы, по которому сумма сил остается неизменной, существует другой, не менее общий и не менее согласный с разумом закон: в телах, связанных друг с другом, а также и во всей природе общее количество направления остается неизменным»⁹.

Под «направлением» Лейбниц понимал здесь количество движения как геометрическую величину, а сумму количеств движения — как геометрическую сумму. При этом он подчеркивал, что сохранение этой величины в природе «не удовлетворяет тем требованиям, которые предъявляются к абсолютному. Ибо возможно, что скорость, количество движения и сила тел будут весьма велики, а их движение вперед будет равно нулю»¹⁰.

В природе должно сохраняться нечто, сохранение которого абсолютно, утверждал Лейбниц. Этим абсолютным является «сила». Сила измеряется произведением массы на высоту или для тела, упавшего с высоты, — произведением массы на квадрат скорости. Эта величина сохраняется и при соударении шаров, как показал еще Гюйгенс, и должна, вообще говоря, сохраняться в природе. Этот закон сохранения Лейбниц назвал законом сохранения живых сил.

Лейбниц ввел также понятие «мертвой» силы. «Мертвая» сила— это сила, которая не производит движение, а лишь стремится произвести его, например это тяжесть, действие сжатой пружины и т. п. «Мертвая» сила измеряется мерой Декарта, т. е. произведением массы на скорость, которую она сообщила бы телу в первый момент своего действия. Между «живыми» и «мертвыми» силами существует определенная связь: живая сила как бы рождается в результате бесконечного количества непрерывных действий «мертвой» силы. Учение о живых силах Лейбниц положил в основу учения о движении, названного им динамикой. Он пытался дать общую систему механики, в основе которой лежал закон живых сил. Вопрос о мере «силы» или движения вызвал горячие споры, которые длились довольно долгое время.

¹Галилей Галилео. Избранные труды. Т. II, с. 246.
²Галилей Галилео. Избранные труды. Т. II, с. 256.
³Гюйгенс X. Три мемуара по механике. М., Изд-во АН СССР, 1951, с. 122.
⁴Там же, с. 124.
⁵Например, массы могут подпрыгнуть вверх после упругого удара о наклонные плоскости.
⁶Гюйгенс X. Трн мемуара по механике, с. 223.
⁷> Гюйгенс. X Три мемуара по механике, с. 366.
⁸Там же, с. 235.
⁹Leibnitz G. Mathematische Shriften. В. VI. Herausgegeben, von Gerhardt, I860, s. 127.
¹⁰Там же, s. 217.

<<Назад Вперёд>>

Просмотров: 5399

загрузка...

Другие книги по данной тематике