Вечное движение и физика
|
Попытаемся рассказать о законах природы, исключающих возможность создания перпетуум-мобиле.
Постройте машину, которая совершала бы работу большую, чем сообщенная ей энергия, и вы решите проблему вечного движения. Чтобы вечный двигатель мог работать, он должен сам себя обеспечивать энергией. Иначе говоря, он должен вырабатывать ее в достаточном количестве, не имея никакого внешнего источника. Представьте, что нужно рассчитать баланс энергии, затрачиваемой на совершение того или иного вида работы, будь то движение океанского лайнера, или забивание гвоздей, или полет со сверхзвуковой скоростью. В любом случае количество затраченной энергии всегда должно быть равно количеству энергии, произведенной или выделившейся в результате совершения работы. Энергия, которую мы не совсем точно называем потерянной, на самом деле не исчезает. Просто она переходит в иную форму, при этом исключается возможность ее дальнейшего превращения в механическую или электрическую энергию. Так получается оттого, что в результате трения происходит нагревание и часть энергии выделяется в виде тепла. И это, вообще говоря, справедливо для потерь любого вида энергии, ибо они в конечном счете всегда превращаются в тепло. Эту же мысль можно выразить и иными словами: во всех случаях общая конечная сумма энергии равна ее общей начальной сумме. Энергия не возникает и не исчезает, но переходит в другую форму, иногда малополезную или совсем бесполезную. Например, тепло, выделяемое в двигателе внутреннего сгорания, — ненужный и тем не менее неизбежный продукт превращения энергии. Его можно использовать, скажем, для обогрева салона автомобиля, но сделаем ли мы это или не сделаем — все равно часть работы, совершаемой двигателем, будет тратиться на тепловые потери. Все, о чем говорилось выше, и представляет собой суть важнейшего закона природы — закона сохранения энергии, или первого начала термодинамики. Мы уже говорили, что вечный двигатель должен совершать полезную работу, не имея никаких внешних источников энергии. Проще сказать, в нем не должно сжигаться топливо и к нему не должны прикладываться механические усилия. Существует ряд свидетельств, что именно поиски такой не реализуемой на практике машины заложили фундамент механики как науки. Великие ученые прошлого приняли как аксиому невозможность создания перпетуум-мобиле и тем помогли пробиться росткам новой науки. Порой легко доказать негодность того или иного проекта вечного двигателя и тем самым показать, что данный конкретный способ его реализации не приведет к желаемому результату. Но это вовсе не означает, что автоматически исключается возможность построения перпетуум-мобиле другими средствами. Поэтому, до тех пор, пока не был четко сформулирован закон сохранения энергии, невозможность создания механического вечного двигателя, установленная многовековым опытом, вовсе не означала невозможность создания, скажем, двигателя химического. Конечно, бесплодность поисков вечного движения признавалась еще до того, как этот закон стал достоянием науки. Однако это мнение основывалось не на некоторых общих положениях, а на анализе принципа действия отдельных «машин вечного движения». Тщательное рассмотрение очередного проекта всегда обнаруживало какие-нибудь теоретические ошибки, из-за которых двигатель не мог работать, а претензии изобретателя оказывались несостоятельными. В разработку общепринятого ныне критерия неосуществимости вечного движения, провозглашающего невозможность создания энергии из ничего, внесли свой вклад философы, математики, инженеры. Закон сохранения энергии стал неизбежным препятствием для изобретателей перпетуум-мобиле. И все попытки преодолеть это препятствие кончались крахом. Но вскоре было сформулировано еще общее положение, получившее название второго начала термодинамики. Это начало, говоря несколько упрощенно, гласит, что тепло не может увеличиваться самопроизвольно; иными словами, если более нагретое тело привести в контакт с менее нагретым, то будет наблюдаться выравнивание температур, а не увеличение их разности. Это явление (выравнивание температур) долгое время не имело никакого теоретического объяснения. Впервые сформулированное немецким физиком Рудольфом Юлиусом Эммануэлем Клаузиусом (1822-1888), второе начало термодинамики носило чисто эмпирический характер. Правда, указывалось на аналогию между изменением температуры контактируемых тел и потоком воды, текущей вниз под действием собственной тяжести, но ситуация осложнялась тем, что.не удавалось установить, какие же внешние силы управляют этим тепловым процессом. Поэтому, хотя эксперимент всегда обнаруживал уменьшение температуры, вплоть до последней четверти прошлого столетия высказывались сомнения относительно всеобщности второго начала термодинамики. Более того, некоторые ученые пытались опытным путем доказать, что существуют случаи, нарушающие справедливость этого начала. В 1875 году вышла в свет знаменитая «Теория теплоты» Максвелла, в которой утверждалось, что характер действия второго начала термодинамики может быть уточнен следующим мысленным экспериментом. Если представить себе некое устройство, которое сортировало бы молекулы по их скорости, то можно было бы без затраты работы и не нарушая закона сохранения энергии нагревать одну половину некоторого объема газа и охлаждать вторую. Результатом этого мысленного эксперимента и будет увеличение тепла в одной части сосуда с газом и уменьшение в другой. Видоизмененное таким образом второе начало термодинамики приобрело вероятностный, а не детерминированный характер. В конце прошлого столетия физики Больцман и Планк заложили научные основы этого вопроса. Больцман, в частности, показал, что самопроизвольное выравнивание температур двух тел есть результат перехода молекул этих тел из менее вероятного в более вероятное состояние. Гипотетическая передача тепла в направлении от менее нагретого тела к более нагретому в свете этого доказательства возможна, но маловероятна. Это положение можно проиллюстрировать простым примером. Закон диффузии газов очень близок к закону теплопереноса, поскольку в процессе диффузии молекулы газов стремятся распределиться равномерно. Если на газ не воздействовать извне, то будет наблюдаться тенденция к выравниванию его плотности. Было бы по меньшей мере странно, если бы газ, первоначально обла- давший равномерной плотностью, вдруг стал бы скапливаться в одной части сосуда, оставляя при этом незаполненное пространство в другой его части. Аналогичное весьма маловероятное явление происходило бы с теплом, переходящим от менее нагретого к более нагретому телу. Давайте теперь предположим, что существует крохотный сосуд, вмещающий всего две молекулы, по одной в каждой половине сосуда. Молекулы эти находятся в непрерывном движении, ударяясь о стенки и беспорядочно проскакивая вперед и назад из одной части сосуда в другую. При этом, очевидно, существуют четыре возможных варианта расположения молекул в пространстве: А - В, В - А, АВ <- 0, 0 -> АВ. В двух вариантах из четырех в одной половине сосуда возникает вакуум. Следовательно, вероятность такого события равна 1/2, и можно ожидать, что половину времени одна часть сосуда будет пустой. С увеличением числа молекул вероятность появления вакуума резко падает. При общем числе молекул, равном n, вероятность того, что половина сосуда окажется пустой, составит (l/2)n-1. Практически число молекул огромно, поэтому вероятность такого события близка к нулю. Так, для реального случая, когда разница давлений в двух половинках одного кубического сантиметра газа не превышает одного процента, вероятность возникновения вакуума в какой-нибудь половине этого кубика ничтожно мала; такое событие может произойти один раз за 101018 лет! И хотя эти рассуждения выглядят вполне впечатляющими, одно обстоятельство все же необходимо пояснить. Не следует думать, что если возникновение вакуума — событие настолько редкое, то нам действительно придется ждать его появления многие миллионы лет. Вакуум может создаться и через минуту! Более того, вакуум может возникнуть дважды в течение минуты, но на очень короткое время. Доктор Хейл из бюро стандартов США предположил, что подобная система доказательств могла бы привести нас к аналогичному заключению о возможности самопроизвольного появления заметной разницы температур в некоем объеме газа. Известно, что температура газа определяется скоростью движения его молекул. При температуре, которая считается постоянной, скорости отдельных молекул газа далеко не одинаковы. Однако все они статистически распределены около той средней величины, которая всегда остается неизменной. Давайте вновь рассмотрим микроскопический сосуд, в котором находится всего четыре молекулы. Пусть на этот раз две молекулы F1 и F2 быстрые, а две другие молекулы S1 и S2 медленные. Допуская, что изменений в плотности газа нет, мы получим шесть различных вариантов расположения молекул в сосуде: F1S1 - F2S2 F2S1 — F1S2 F1S2 — F2S1 F2S2 — F1S1 S2S1 — F1F2 F1F2 — S1S2 Первые четыре варианта — это случаи, когда в обеих половинах сосуда температура газа одинакова, поскольку современные измерительные приборы дают ее усредненное значение. В двух последних вариантах наблюдается разница температур; вероятность их возникновения для четырех молекул равна 1/3. С увеличением числа молекул вероятность появления сколько-нибудь заметной разницы температур в двух частях нашего гипотетического сосуда резко уменьшается. Следует также иметь в виду, что в любом объеме газа, температуру которого мы в состоянии измерить или проконтролировать, температура каждой отдельной весьма малой его части постоянно колеблется относительно градуировочной кривой прибора, и в целом газ столь же неоднороден по температуре, как и поверхность океана не является абсолютно ровной. Итак, вероятность появления заметной разницы температур в газе очень мала. Но все же она существует, и, значит, следует не только признать возможность перехода тепла от менее нагретого тела к более нагретому, но и согласиться с тем, что такой переход непрерывно осуществляется, правда, в столь незначительных масштабах, что мы вряд ли сможем его наблюдать. Поэтому, как утверждал немецкий философ Карл Христиан Планк (1819-1880), существует вероятность, хотя и очень незначительная, что в чайнике, помещенном над огнем, замерзнет вода. Признание учеными возможности, во-первых, перехода тепла от менее нагретого тела к более нагретому и, во-вторых, возникновения при этом незначительного, но все же заметного изменения температуры и плотности послужило основанием для дальнейших рассуждений. Возник вопрос о том, нельзя ли создать устройство, в котором в результате подобных изменений постепенно увеличивался бы перепад температур, за счет которого можно было бы в дальнейшем совершать полезную работу? Вопрос этот возник лет восемьдесят назад, а само это гипотетическое устройство вошло в науку под названием вечного двигателя второго рода. Такое название оно получило потому, что должно было совершать работу, не вырабатывая энергии и вопреки второму началу термодинамики. Проект устройства был сперва предложен парижанином Липпманом в 1900 году, а затем в 1907 году Сведбергом из города Упсала (Швеция). В 1912 году Смолуховский опубликовал развернутое теоретическое обсуждение данной проблемы. Он показал, что вряд ли стоит надеяться, будто с помощью устройства, содержащего молекулы газа, удастся накапливать эти столь редкие «отступления» от второго начала, поскольку любое подобное устройство само по себе будет подвержено изменениям на молекулярном уровне. Постоянно происходящее перераспределение скоростей движения молекул уничтожит все перепады температуры, которые предполагалось накапливать в устройстве и которые принципиально необходимы для его работы. Это доказательство представляется весьма убедительным, хотя и обескураживающим. Замечателен вывод, вытекающий из него: второе начало термодинамики для больших промежутков времени справедливо лишь в статистическом смысле. Интересно, что спустя тринадцать лет, в марте 1925 года, выступая перед сотрудниками американского бюро стандартов, профессор Дебай заявил: для согласования явления интерференции света с квантовой теорией необходимо допустить, что закон сохранения энергии верен только в статистическом смысле. По его мнению, в очень короткие промежутки времени энергия может создаваться, а на протяжении длительного времени ее среднее значение будет оставаться неизменным. В предположении Дебая содержится скрытый намек на то, что вечное движение первого рода, то есть истинное создание энергии, представляет собой некую «научную вероятность» и даже «возможность». Поиски вечного движения можно отнести к числу тех научных заблуждений, которые пришли на смену опытам алхимиков и построениям квадратуристов. Однако столетия, в течение которых умы ученых мужей были заняты подобными тщетными исканиями, обогатили науку знаниями, куда более ценными, чем цели, преследуемые этими фанатиками. Вот что писал по этому поводу в своей «Теории теплоты» Престон: «Алхимики сделали для химии как науки то же, что изобретатели вечных двигателей для натурфилософии. Их поиски неизбежно привели к открытиям величайшей теоретической и практической важности». Одним из первых осознал важность проблемы вечного движения для экспериментальной науки Симон Стевин, родившийся в 1548 году в Брюгге. Этот великий математик был также человеком практики: среди его изобретений, относящихся к началу XVII века, есть повозка под парусами, на которой он катался вместе с друзьями по побережью Нидерландов. Стевин был ярым сторонником десятичной денежной системы и десятичных дробей (напомним, что эти дроби тогда еще не получили повсеместного применения в практике повседневных вычислений); он ввел в физику понятие устойчивого и неустойчивого равновесия. Однако наиболее важным его достижением в контексте данной книги является доказательство закона равновесия тел на наклонной плоскости, которое он получил, показав, что вечного движения не существует. Его рассуждения сводились к следующему. Вообразим, что на гибкий шнур, соединенный в кольцо, на равном расстоянии друг от друга нанизано четырнадцать шаров, одинаковых по весу. Шнур подвешен на подставку треугольной формы, состоящую из двух неравных наклонных плоскостей и одного общего горизонтального основания. Не нарушая общности рассуждений, положим ради простоты, что АС = 2ВС, а на участке АЕВ шнура расположено восемь шаров. При этом возможны два случая: либо шары находятся в состоянии равновесия, либо равновесие отсутствует. В последнем случае начнется движение шаров, которое, однако, не изменит их первоначального расположения на подставке. На участке АЕВ всегда будет восемь шаров, на плоскости АС — четыре, а на плоскости ВС — два. Следовательно, движение такой системы будет непрерывным, иными словами, вечным. Стевин не только не допускал этого, но считал нарушение равновесия в таких условиях совершенно невозможным. В своей книге по теории наклонных плоскостей, опубликованной в конце шестнадцатого столетия, он подробно рассмотрел эту проблему. Прежде всего он показал, что при удалении восьми шаров с участка АЕВ равновесие не нарушается, поскольку четыре шара на кривой АЕ уравновешивают четыре шара на кривой ЕВ. Именно по этой причине и сохраняется равновесие между четырьмя шарами на большей плоскости (АС) и двумя шарами на меньшей (СВ). Если даже расположить плоскость СВ вертикально так, что останется только одна наклонная плоскость АС, условие равновесия будет по-прежнему выполняться. Таким образом, мы нашли, что соотношение сумм весов шаров должно быть таким же, как соотношение между длинами плоскостей, то есть 4x2 = АСxВС. Если теперь принять сумму весов двух шаров за действующую силу, а сумму весов четырех шаров за противодействующую, то получится следующая пропорция: противодействующая сила длина действующая сила длина ----------------------------------------------- = ------ действующая сила высота
Это хорошо известное условие равновесия сил на наклонной плоскости, когда направление действующей силы параллельно наклонной плоскости. Эрнст Мах (1838-1916), австрийский физик и популяризатор науки, высоко ценил труды Стевина. Однако Мах считал, что в большинстве своем выводы фламандского ученого основаны на чисто эмпирических наблюдениях.
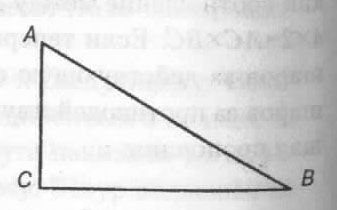
Вот что писал он по этому поводу в своей «Механике»: «Совершенно ясно, что в исходных предположениях Стевина о неподвижности бесконечной цепи содержатся утверждения чисто интуитивного характера. Он сам верит, и мы верим вместе с ним, что движение в подобных условиях никогда и никем не наблюдалось, что оно просто не существует. Это утверждение столь логично, что мы принимаем все вытекающие из него выводы относительно закона равновесия. Доводы Стевина впечатляют своей оригинальностью, а результаты его рассуждений содержательнее первоначальных предположений». Другим ученым, отрицавшим возможность существования вечного движения, был Галилей (1564-1642). Это ясно видно из его работы, посвященной сравнению движения тел по наклонной плоскости с их свободным падением. Он предположил, что скорость, приобретаемая телом при движении из точки А в точку B (если пренебречь силой трения), должна быть равна скорости тела в точке С при его свободном падении из точки А. В противном случае, доказывал Галилей, шар, двигаясь вверх по наклонной плоскости, подымался бы выше того уровня, с которого он скатился, независимо от наклона плоскости и собственного веса. Однако чисто теоретические рассуждения не удовлетворяли первоклассного экспериментатора. Он решил проверить свои выводы на практике. Схема эксперимента, который осуществил Галилей, изображена на рис. 3. Один конец гибкого шнура привязан к гвоздю, вбитому в стену, на другом конце подвешен тяжелый шар.
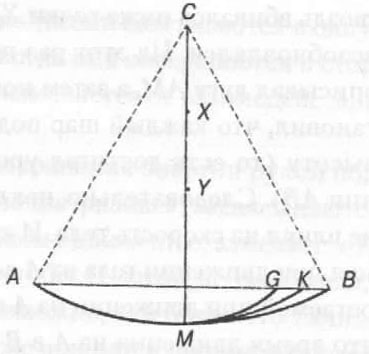
Поднимая шар маятника из положения М в положение А так, чтобы при этом сохранялось натяжение нити, а затем отпуская его, Галилей установил, что шар поднимается на ту же высоту по другую сторону от вертикальной линии. Небольшое расхождение высот он отнес за счет сопротивления воздуха. Затем он видоизменил эксперимент. В точке X справа от вертикально висящего шнура в стену вбивался еще один гвоздь. Теперь шар описывал дугу AM, а когда шнур зацеплялся о гвоздь, часть шнура СХ прекращала движение, и шар описывал новую дугу МК. Третий гвоздь вбивался ниже точки X, в точке Y, и эксперимент возобновлялся. На этот раз шар, как и раньше, сперва описывал дугу AM, а затем новую дугу MG. Ученый установил, что каждый шар поднимался на одну и ту же высоту (то есть достигал уровня горизонтальной линии АВ). Следовательно, наклон плоскости (см. рис. 2) не влиял на скорость тела. И хотя скорость, приобретаемая при движении тела из A в С, равна скорости, приобретаемой при движении из A в В, из этого не следовало, что время движения из А в В равно времени движения из A в С. Вслед за Галилеем Марен Мерсенн (1588-1648) категорически отрицал возможность существования вечного движения, а все попытки построить вечный механизм сравнивал с поисками алхимиками философского камня. Христиан Гюйгенс (1629-1695), по-видимому, был совершенно незнаком с работой Галилея, когда решил с помощью маятника экспериментально доказать, что центр тяжести тела, свободно движущегося под действием силы тяготения, не может подняться выше точки, откуда началось его движение. Голландский ученый верил, однако, в возможность создания вечного двигателя, но не с помощью сил тяжести, а посредством использования других естественных явлений и прежде всего магнитного притяжения и отталкивания. Как ни странно, бытует мнение, будто Исаак Ньютон (1642-1727) заблуждался относительно невозможности получения вечного движения. Произошло это, вероятно, оттого, что ни в одной из своих книг Ньютон не оставил прямых упоминаний об этой проблеме. В его «Принципах» таким общим понятием, как работа и энергия, отведена второстепенная роль. Но в следствии к третьему закону движения Ньютон формулирует следующее положение: «Количество движения, получаемое как сумма количеств движений, когда они совершаются в одну сторону, и как разность, когда они совершаются в стороны противоположные, не изменяется от взаимодействия тел между собою». Отсюда до закона сохранения энергии рукой подать. Манн в книге «Обучение физике», касаясь ньютоновского отношения к вечному движению, замечает: «Трудно представить себе, чтобы Ньютон не осознавал, что вечное движение невозможно, тем более что Галилей и Гюйгенс интуитивно уже пришли к такому заключению. Гораздо вероятней предположить, что, понимая сущность проблемы, он просто не упоминал о ней в своих книгах. Поскольку учение о теплоте находилось тогда в зачаточном состоянии, он не мог говорить о вечном движении с той строгостью, с которой он рассматривал другие вопросы механики». Роже, критикуя электрическую контактную теорию Вольта, интуитивно использовал идею отрицания вечного движения. В книге «Гальванизм», вышедшей в свет в 1832 году, он писал: «Все силы и источники движения, причины которых нам известны, при совершении ими свойственных им действий иссякают в той же мере, в какой эти действия возникают, а отсюда вытекает невозможность непрерывного образования ими эффекта, или, другими словами, они не могут вызывать непрерывно возникающего движения. Однако электродвижущая сила, которую Вольта приписывает находящимся в контакте металлам и которая, пребывая в свободном состоянии, является источником электрического движения, никогда не иссякает и продолжает использоваться с неуменьшающейся интенсивностью, производя непрекращающееся действие. Справедливость такого положения можно опровергнуть бесчисленными действиями». Эти рассуждения появились всего за несколько лет до того, как был четко и строго сформулирован закон сохранения энергии. Карно использовал идею неосуществимости вечного движения в качестве одного из принципов, позволивших ему установить связь между работой, производимой машиной, и теплом, получаемым в ее котле. Другим принципом был так называемый принцип сохранения калорий. И хотя этот принцип позднее был отвергнут в связи с тем, что появилась общепризнанная ныне динамическая теория, работа Карно долгое время оставалась выдающимся вкладом в понимание проблем энергетики. Примерно в то же самое время Фарадей использовал идею отрицания вечного движения в своих рассуждениях, опровергающих контактную теорию Вольта. Вернемся, однако, к законам, препятствующим созданию перпетуум-мобиле. Первое начало термодинамики гласит, что при совершении определенного количества механической работы всегда выделяется эквивалентное количество тепла. Поэтому энергия переходит из одной формы в другую, но не создается и не уничтожается. Повторю, что именно на этом положении основывается закон сохранения энергии. Второе же начало термодинамики — в простейшей его форме — утверждает, что количество тепла не может увеличиться без совершения дополнительной работы (или, как мы уже говорили, не может переходить от менее нагретого тела к более нагретому). Немецкий врач Юлиус Роберт Майер (1814-1878), размышляя над сущностью первого закона термодинамики, писал в 1842 году: «Возникнув, сила не может исчезнуть, она может лишь видоизменить свою форму». Другой выдающийся ученый Герман Гельмгольц (1821-1894), будучи еще молодым человеком, смог убедить ученый мир в том, что первый закон термодинамики верен. Двадцатишестилетний естествоиспытатель представил на суд физического общества в Берлине свою работу, озаглавленную «О сохранении силы». Анализ проблемы он начал с утверждения, что невозможность создания машин вечного движения является аксиомой. Верность аксиомы в физике может быть установлена наблюдением за систематически повторяющимися природными явлениями или экспериментально. Но Гельмтольцу не нужно было заниматься доказательствами: достаточно было сослаться на то, что все попытки построить вечный механизм кончились неудачей. С подобной аксиомы и начал свою работу Никола Леонар Сади Карно (1796-1832), французский физик и один из первых теоретиков паровых машин. Отрицание вечного движения легло в основу многих его выводов по теплотехнике. Книга Карно «Размышления о движущей силе огня» (1824) заложила фундамент второго начала термодинамики. Стэнли Ангрист справедливо заметил, что проекты некоторых вечных механизмов не противоречили первому началу термодинамики, поскольку ни трение, ни электрическое сопротивление не влияли на их работу1. Тем не менее эти перпетуум-мобиле также не были реализованы, потому что их создатели пытались обойти второе начало термодинамики, согласно которому определенное количество механической работы может всегда быть превращено в эквивалентное количество тепла. А вот обратный переход, то есть превращение некоторого количества тепла в то же самое количество работы, невозможен по той простой причине, что часть тепловой энергии неизбежно теряется. В паровой машине основные потери тепла (тепловой формы энергии) происходят из-за трения, нагрева самой машины и передачи тепла в окружающее пространство. Карно тщательно изучил замкнутый цикл работы паровой машины, в течение которого вода нагревается до превращения в пар, пар движет поршень, затем конденсируется, превращаясь в воду, вновь поступающую в котел машины. Он пришел к заключению, что в процессе охлаждения и конденсации пара происходят неизбежные потери тепловой энергии, и поэтому преобразование тепла в движущую силу «определяется исключительно температурой тел, между которыми происходит передача калорий» (теплообмен). Открытие Карно представляет собой, по существу, первую формулировку второго начала термодинамики: совершая работу, тепло ведет себя подобно потоку воды в водяной мельнице, текущему сверху вниз. И чем больший путь вода при этом проделывает, тем большую совершает работу. Мы же говорили, что для совершения работы теплота должна передаваться от более нагретого тела к менее нагретому. Идеи Карно были развиты Клаузиусом. Он ввел в науку термин «энтропия», характеризующий количество безвозвратно потерянного тепла. Ангрист пишет: «Современная формулировка второго начала термодинамики, гласящая, что энтропия постоянно увеличивается, возникла из более ранних представлений о направлении движения тепла. Поскольку общее количество энергии во Вселенной постоянно, оно не может уменьшаться или увеличиваться. Вместе с тем движение теплоты сопровождается неизбежными потерями. Поэтому наступит такое время, когда во Вселенной установится одна и та же температура. Поскольку при этом не будет более разницы температур между отдельными телами, а следовательно, по терминологии Карно, и переноса калорий, не будет совершаться работа. Этот неизбежный конец мира называют иногда "тепловой смертью". Мы же говорим о нем по следующей причине. Если бы удалось создать вечный двигатель, работа которого противоречила бы второму началу термодинамики, то это позволило бы не только локально приостановить рост энтропии, но даже добиться ее уменьшения. Тот факт, что в среднем энтропия непрерывно растет, не исключает, конечно, возможности ее случайного локального уменьшения. Просто вероятность такого события слишком мала». Пожалуй, так же мала, добавим мы, как и в описанном выше случае с чайником, в котором вода в принципе может замерзнуть, вместо того чтобы закипеть. Химик Генри Бент вычислил вероятность локального уменьшения энтропии, исходя из условия полного превращения одной калории тепловой энергии в работу. Бент остроумно сравнил это событие с изданием полного собрания сочинений Уильяма Шекспира группой обезьян, случайным образом нажимающих на клавиши пишущей машинки. Он показал, что вероятность такого превращения калории равна вероятности того, что обезьяны смогут пятнадцать квадриллионов раз подряд без единой ошибки ударить по нужным клавишам и таким образом напечатать все, что создал Шекспир. 1 Машины вечного движения. — «Сайентифик Америкэн», 1968, январь, т. 218, с. 114-122. |
загрузка...