XXI. «Новые начала геометрии с полной теорией параллельных»
|
Мы уже говорили о том, что наиболее плодотворную научную деятельность Лобачевский развернул именно в те годы, когда он стоял во главе университета. «Совершенно изумительно, — замечает Энгель1,—какую огромную научную продукцию он дал именно в эти годы, когда он был так перегружен преподавательской и административной работой». Главным произведением, опубликованным Лобачевским во второй период управления университетом, было самое обширное из его сочинений «Новые начала геометрии с полной теорией параллельных». Оно начало печататься в «Ученых записках университета» в том же 1835 г. в III книжке, т. е. непосредственно после того, как была опубликована «Воображаемая геометрия». Печатание продолжалось в 1836 и 1837 гг. и было закончено только в III книжке за 1838 г.
Мы до сих пор говорили только о тех идеях Лобачевского, которые привели к неевклидовой геометрии и составляют ее содержание. Но, по существу, замысел Лобачевского был гораздо шире: это тот же замысел, который так часто ставили себе комментаторы Евклида: дать безукоризненное построение начал геометрии. Первые шаги в деле осуществления этого замысла мы находим уже в «Геометрии». Несомненно, и самое создание неевклидовой геометрии находится с этим в тесной связи. Дать все построение геометрии ab ovo с учетом двух возможных гипотез в теории параллельных линий, т. е. евклидовой и «воображаемой» геометрии, показать как их разветвление, так и их объединение в одну более общую систему, — такова задача этого сочинения. Обстоятельно изложить построение начал неевклидовой геометрии действительно было уже необходимо. В мемуаре «О началах геометрии», как мы видели, самые основы неевклидовой геометрии изложены конспективно, в такой сжатой форме, что уяснить себе их по этому очерку было невозможно. В мемуаре «Воображаемая геометрия» Лобачевский исходит из готовых уже уравнений, связывающих стороны и углы треугольника; они кажутся неожиданно упавшими с неба; Лобачевский и сам говорит, что такое априорное задание аналитической базы может вызвать у читателя изумление; чтобы устранить возникающее недоумение, Лобачевский вновь отсылает читателя к сочинению «О началах геометрии»; получается заколдованный круг. Чтобы из него выйти, Лобачевский считает необходимым изложить всю геометрию сначала, и притом чисто синтетически. «Главная выгода в анализе та,— пишет Лобачевский во «Вступлении»,— что здесь от уравнений идут всегда прямой дорогой к предположенной цели. Синтез не подчиняется каким-нибудь общим правилам, но с него надо начинать по необходимости, чтобы, наконец, отыскав уравнения, достигнуть с тем вместе той черты, за которой все переходит уже в науку чисел... Напрасно хотели бы такой случай, как и всю теорию параллельных, рассматривать аналитически». Это не совсем так; но в эпоху Лобачевского идея о полной арифметизации геометрии была еще математикам совершенно чужда: она возникла только в связи с развитием идей самого Лобачевского. Так или иначе, Лобачевский становится на путь чисто синтетического построения геометрии с самого начала, т. е. на путь, по которому шли Евклид и его последователи. Что побуждает Лобачевского вступить на этот путь? Вот что он говорит об этом в обзоре преподавания геометрии в 1824—1825 уч. г.2: «Начала геометрии казались некоторым столь легки, что они предлагали проходить их прежде арифметики и алгебры. Однакож естьли в математике строгость необходима, то начала геометрии представляют трудности, которые должно встретить зрелому уму, суждением укрепленным предшествовавшим уже учением математики. Не указать на них, значило бы сделать важное опущение в преподавании, потому что воспитанники университета готовятся сами быть наставниками, через них ожидают распространения просвещения, что они могут вести его и далее, а следовательно, они должны учиться всему основательно». И далее, в следующем обзоре3: «Другого рода трудность в геометрии представляет параллелизм линий, трудность до сих пор непобедимую, но между тем заключающую в себе истины ощутительные, вне всякого сомнения и столь важные для целой науки, что никак не могут быть обойдены. Итак, остается только все сии истины привести к одной такой, которая бы могла легко убеждать в ее справедливости, присоединяя сюда некоторые пояснения, несмотря на недостаток строгости». Итак, преодолеть те затруднения, которые, с одной стороны, представляет общее обоснование начал геометрии, которые, с другой стороны, коренятся в теории параллельных линий,— таковы две задачи, которые Лобачевский себе ставил, составляя сочинение «Новые начала геометрии с полной теорией параллельных»; эта двойная цель указана уже в самом заглавии книги. Иначе говоря, эта цель заключалась в том, чтобы обстоятельно изложить то, к чему он пришел прп размышлении над этими вопросами, что слишком кратко изложил в предыдущих своих сочинениях. Книга содержит, впрочем, еще третью, дополнительную часть, прямо к этим задачам но относящуюся; о ней будет сказано ниже. «Вступление» содержит критику обоснования геометрии, как оно выполнялось раньше. Лобачевский начинает с разбора наиболее важных попыток доказать постулат о параллельных линиях, останавливаясь главным образом на доказательстве Л. Бертрана и на рассуждениях Лежандра; он разбирает их с тщательностью, какая до него никогда не проявлялась. Разбор каждого доказательства здесь состоит из двух частей: 1) Лобачевский обнаруживает, в чем коренится ошибка доказательства, 2) он показывает, как обстоит дело в неевклидовой геометрии, как в ней теряют доказательную силу те рассуждения, которыми пользуются авторы доказательства. В том и другом отношении особенный интерес представляет собой его анализ доказательства Бертрана; нужно сказать, что и по настоящее время вряд ли есть сочинение, в котором этот анализ выполнен с такой убедительностью. Во всяком случае рассуждения Буняковского4 сильно им уступают. Лобачевский показывает, что основная ошибка Бертрана заключалась в том, что он рассматривает угол как величину, не устанавливая правильных критериев сравнения различных значений величины (различных углов). От этого важного вопроса Лобачевский переходит к разбору тех оснований, на которых вообще строилась геометрия. Точкой его отправления в этой критике служит следующее основное соображение: «...пространство, протяжение, место, тело, поверхность, линия, точка, направление, угол — слова, которые начинают геометрию, но с которыми никогда не соединяют ясного понятия». Никогда до Лобачевского с такой определенностью не высказывалось требование пролить свет на всю совокупность этих понятий. Приведем еще следующий абзац, в котором это требование выясняется: «Геометрию начинают обыкновенно, придавая телам три протяжения, поверхностям два, линиям одно, в точке не допускают никакого. Называя три протяжения: длина, ширина, высота и разумея по этими названиями собственно три координаты, спешат таким образом преждевременные понятия сообщить словами, которым разговорный язык придает уже какое-то, хотя для точной науки еще неопределенное значение. В самом деле, как можно с ясностью себе представлять измерение в длину, когда не знаем еще, что такое прямая линия? Как можно говорить о ширине, высоте, ничего не сказав наперед о перпендикулах, о плоскости, как бывают перпендикулы в одной и в разных плоскостях? Наконец, если в точке нет ни одного протяжения, то что же в ней остается затем, чтобы она могла быть предметом суждения? Пусть и так, что прямую линию всякий ясно себе представляет, хотя не может еще дать отчета в своем понятии; но спрашивается, каким образом помощью прямой должен он назначать теперь однопротяжение в кривой линии, два в кривой поверхности?» Все это нужно выяснить, нужно пролить свет на эти начала геометрии. Однако много легче поставить такие требования, чем их выполнить. Установление основных понятий (категорий), установление связей между ними, из которых их свойства могут, выводиться строго логическим путем, — самая трудная задача во всякой дедуктивной науке, может быть труднее других в геометрии. Рассуждения, возникшие в связи с развитием идей Лобачевского, содержащихся в.его «воображаемой геометрии», и привели к выяснению этих вопросов; но Лобачевский далеко еще не дал их разрешения. Сочинение «Новые начала» состоит из тринадцати глав. Первые шесть глав посвящены изложению абсолютной геометрии и представляют собой развитие того, что изложено в первых пяти главах «Геометрии»: то же расположение материала и по существу та же его обработка. Лишняя глава обусловливается тем, что глава I посвящена первым понятиям в геометрии. Очень трудно точно передать ее содержание: правильные, глубокие мысли чередуются с соображениями, которые нельзя признать обоснованными, надежными в качестве исходной базы, для построения геометрии. Ограничимся немногими указаниями. Основными понятиями Лобачевский считает тело и соприкосновение тел. Тела, с его точки зрения, единственно только и существуют в природе; поверхности, линии, точки - это уже абстракции, связанные с соприкосновением тел. «Прикосновение составляет отличительную принадлежность тел»; мы называем тело геометрическим, если отвлекаемся от всех других его свойств, кроме способности приходить в соприкосновение с другими телами. Эти два понятия «тело» и «прикосновение», из которых Лобачевский хочет исходить, не могут быть признаны основными категориями, действительно пригодными для логического построения геометрии. Оперируя ими, Лобачевский, конечно, постоянно пользуется наглядными представлениями; никаких признаков, аксиоматически их характеризующих, он не дает. Но на одну их особенность необходимо указать — это понятия топологические: тело остается таковым при всяком непрерывном его преобразовании; два тела, находящиеся в соприкосновении, сохраняют таковое, какой бы непрерывной деформации мы их не подвергали. Этому, может быть, не следует придавать чрезмерно большого значения; Лобачевский, конечно, в этом себе ясного отчета не отдавал; но в настоящее время нельзя не отметить, что Лобачевский пытается строить геометрию, исходя из топологических понятий. Как уже указано выше, этот замысел виден уже в первом его сочинении, в «Геометрии». «Два тела А, В, касаясь друг друга, составляют одно геометрическое тело С, где составные части А, В являются каждая порознь, не теряясь в целом С. Обратно, всякое тело С произвольным сечением S разделяется на две части А, В. Здесь под словом сечение не разумеем какую-нибудь новую принадлежность тела, но то же прикосновение, выражая в этот раз уже деление тела на две прикосновенные части. Две части А, В будем называть еще сторонами сечения S в теле С. Так можно себе представлять все тела в природе частями одного целого, называемого пространством». Совершенно ясно, что понятие о сечении этим отнюдь не определено. Мы не склонны здесь входить в критику, так как дефекты такого определения для современного читателя совершенно ясны. Лобачевский отличает поступательные и обращательные сечения. Поступательные сечения делят тело на части, «которые не касаются взаимно через одну» (рис. 33). Обращательные сечения—это такие, каждое из которых увеличивает на два число частей, находящихся в соприкосновении (рис. 34). Это опять понятия топологические. Рассмотрение различных видов соприкосновения приводит к понятиям «поверхность», «линия», «точка». Вслед за 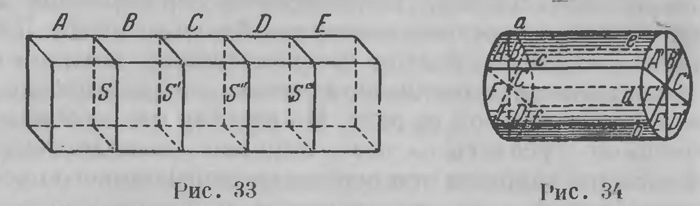
этим Лобачевский переходит к метрическим понятиям. Мы остановимся только на самых важных из них. Установив понятие о теле, Лобачевский определяет «одинаковость» (конгруэнтность) тел и «равенство» (равновеликость) тел. Два тела одинаковы, если могут без всякой с ними перемены наполнять одно и то же место; они равны, если могут быть составлены из равных частей. Обходя уже те трудности, с которыми сопряжено выяснение того, что значит перемещение «без всякой перемены», заметим, что определение равенства (равновеликости) все же дефектно по существу; но понадобилось еще около ста лет, чтобы это отчетливо выяснить5. «Относительное положение двух точек называется расстоянием и назначается прикосновением двух тел, в которых допускаются все те перемены, которые не перемещают точек». Сюда относится и замена тела, содержащего эти точки, другим, которое их также содержит; расстояние фактически определяется как инвариант движения. хотя не со всей необходимой четкостью. Чтобы составить себе ясное представление о взглядах Лобачевского на основные понятия геометрии, необходимо эту главу прочесть полностью. «Вся эта глава, — замечает Энгель6,—оставляет желать многого, и не только потому, что изложение часто страдает неясностью, но главным образом потому, что в развитие предмета автор молчаливо принимает различные допущения, которые при установлении основных понятий не получили выражения». Дать этим допущениям совершенно точное выражение— одна из самых трудных задач. И нельзя слишком строго судить попытку, которую Лобачевский делает для обоснования геометрии. Лобачевский несомненно также пользуется положениями, которые он приводит без доказательств. Он указывает, например, что в учении об измерении «нельзя обойтись без особых вспомогательных положений, которые принимают уже за аксиомы». Между тем аксиом, на которых он строит геометрию, он вовсе не перечисляет. По видимому, это—чрезмерная дань воззрениям Даламбера, опасение впасть в химерическую точность. Но эта точка зрения, может быть, вполне правильная в учебнике, не может получить применение в сочинении, посвященном научному обоснованию геометрии. Лобачевский и сам подчеркивает эту разницу в другом месте; мы отметим это ниже. Располагая понятием о расстоянии, Лобачевский во второй главе определяет плоскость как геометрическое место точек, равноотстоящих от двух точек — «полюсов этой плоскости»; он показывает, как одни полюсы плоскости можно заменить другими; он очень искусно пользуется этим определением. Но свойства плоскости, которыми он в дальнейшем пользуется, не исчерпываются теми, которые в сочинении указаны и которые логически вытекают из данного им определения. Так и в дальнейшем своеобразные определения и логические приемы чередуются с соображениями интуиции, опираются на указание глаза. Вся тенденция логического обоснования геометрии, в том осуществлении, которое мы находим в «Новых началах», не удовлетворяет тем строгим требованиям, которые Лобачевский сам себе ставит. Но очень хорошо и то, что он их ставит; это было стимулом для настойчивых размышлений его последователей. Однако сам он этим требованиям не удовлетворил. Дальнейшие главы, от II до VI, как мы уже указали, представляют собой развитие соответствующих глав «Геометрии»; они свидетельствуют, что Лобачевский в течение многих лет так же настойчиво размышлял над вопросами общего обоснования геометрии, как и над своей «Воображаемой геометрией». Но легче было даже построить новую геометрию, чем строго обосновать старую. 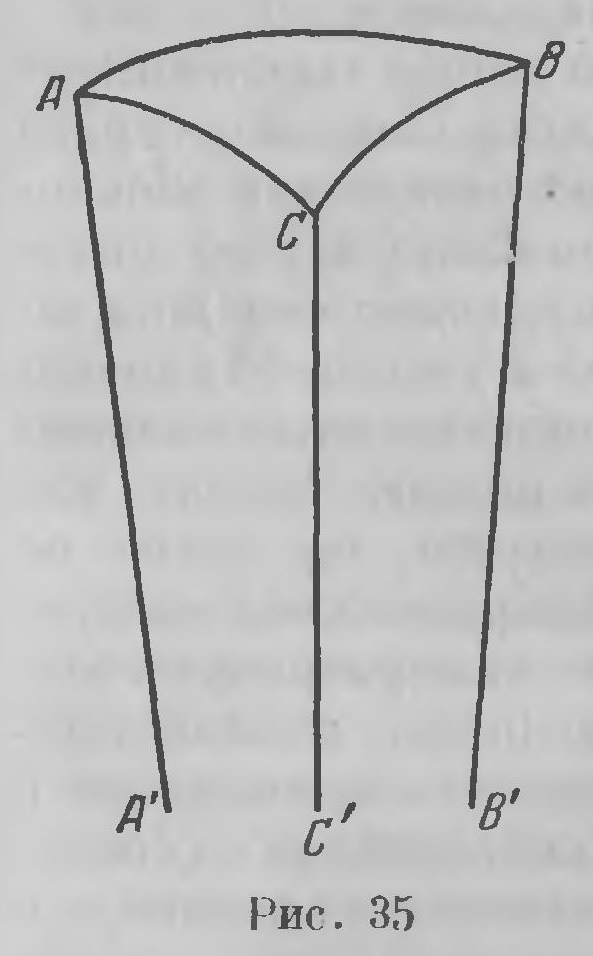
Вторая часть «Новых начал» посвящена всему тому материалу, который зависит от постановки постулата о параллельных, и развертывается по преимуществу так, чтобы расчленение происходило Рис. 35 только там, где это совершенно необходимо; всюду отмечается возможность включения евклидовой геометрии как частного случая в общую новую систему геометрии. В этом отношении основную роль играют те предложения, которые допускают такую формулировку, что остаются в силе как в собственно евклидовой, так и в неевклидовой геометрии. Это кажется странным, но становится ясным из следующего наиболее важного из этих предложений. Представим себе три попарно параллельные прямые, не расположенные в одной плоскости. Три плоскости, проходящие через каждую пару этих прямых, образуют своеобразный триэдр (в специальном значении этого слова) (рис. 35). Сумма внутренних двугранных углов этого триэдра всегда равна 2d, независимо от того, понимаем ли мы параллелизм в евклидовом или в более общем его определении в воображаемой геометрии. И это имеет не только принципиальное, но и решающее значение: если представим себе поверхность, ортогонально секущую все лучи связки параллелей, и на ней будем разуметь под геодезическими сечения ее плоскостями, проходящими через лучи этой связки, то на ней сумма внутренних углов геодезического треугольника всегда равна двум прямым. Именно эту поверхность Лобачевский называет предельной поверхностью; формулированное выше предложение устанавливает, что на предельной поверхности сумма внутренних углов геодезического треугольника равна двум прямым; а это ведет к тому, что на предельной поверхности, независимо от того, принимаем ли мы на плоскости постулат Евклида или Лобачевского, всегда имеет место вся планиметрия Евклида. Значение этого факта уже достаточно было выяснено в главе XV (стр. 198); на нем строится вывод общих тригонометрических уравнений. Эти уравнения содержались в «Exposition succincte», но до нас в этом виде не дошли. В мемуаре «О началах геометрии» вывод их изложен в чрезвычайно схематическом виде; в «Воображаемой геометрии» он вовсе не дан; только здесь, в «Новых началах» он изложен строго синтетически, с безукоризненной точностью, но все же, как всегда у Лобачевской очень сжато. Уравнениями тригонометрии заканчивается глава XI. В «Новых началах» неевклидова геометрия изложена несравненно более четко и ясно, чем в предыдущих сочинениях Лобачевского, и все же изложение еще страдает чрезмерной сжатостью. Главы XII и XIII «Новых начал» по содержанию своему, можно сказать, не связаны с предыдущим. Энгель, который перевел «Новые начала» на немецкий язык, вовсе опустил эти главы. Содержание их заключается в следующем. Лобачевский рассматривает различные случаи решения прямолинейного и сферического треугольника и тщательно определяет предел погрешности при вычислениях с семизначными логарифмами. Так как, однако, вычисления, смотря по заданиям, могут давать более или менее благоприятные результаты, то Лобачевский в последней главе (XIII) обращается к соображениям теории вероятностей и устанавливает вероятную ошибку вычислений. Это особенно существенно в тех случаях, когда данные, по которым вычисление производится, являются результатами кратных наблюдений и потому сами устанавливаются только с некоторой вероятностью. Все результаты поясняются на довольно многочисленных примерах. Эти две главы в несколько переработанном и сокращенном виде Лобачевский опубликовал в 1842 г. на французском языке в журнале Крелля7. Из трех частей, на которые сочинение «Новые начала» таким образом разбивается, наибольшее значение имеет вторая часть — построение основ воображаемой геометрии. Это изложение таково, что вдумчивый человек с общей математической подготовкой несомненно мог его понять. Однако уже «вступление» представляло некоторые затруднения для читателя вследствие содержащихся в нем ссылок на «Воображаемую геометрию» (хотя читатель мог их здесь и опустить). Следующая за вступлением первая часть, очень своеобразная по своей конструкции, вызывающая немало возражений в определениях общих понятий, по видимому, еще более затрудняла читателя. Очень вероятно, что читатель останавливался раньше, чем доходил до главы VIII. Насколько можно судить, никто этого сочинения в то время не прочитал. Лобачевский решил тогда написать небольшое сочинение, короткое и возможно более доступное, которое читатель мог бы легче усвоить. Такое сочинение им было опубликовано в 1840 г. Это и была небольшая книга «Geometrische Untersuchungen», содержание которой, именно вследствие его доступности, уже было изложено выше. В предисловии Лобачевский указывает, что первый опыт изложения этих идей появился уже в «Казанском вестнике» за 1829 г. «В надежде, что я удовлетворил всем требованиям, я затем занялся обработкой этой науки в целом и эту свою работу я опубликовал в «Ученых записках Казанского университета» за 1836, 1837, 1838 гг. отдельными частями под заглавием «Новые начала геометрии с полной теорией параллельных». Однако размер этой работы, по видимому, мешает моим соотечественникам проследить за этим предметом, который после Лежандра утратил интерес. Я же придерживаюсь мнения, что теория параллельных линий отнюдь не потеряла права на внимание геометров, я намерен поэтому изложить здесь самое существенное из моих исследований. Поэтому я считаю нужным уже вперед указать, что вопреки мнению Лежандра все другие несовершенства, как, например, определение прямой линии, оказываются здесь совершенно чуждыми этому вопросу и не имеют никакого влияния на теорию параллельных линий». Такова задача, которую Лобачевский себе ставил, составляя «Геометрические исследования». Мы уже знаем, что эта небольшая книга тоже получила неблагоприятный отзыв (см. выше, стр. 262); но, как сказано, именно эта брошюра обратила на себя внимание Гаусса. После смерти Гаусса в его библиотеке были найдены два экземпляра «Geometrische Untersuchungen». 11 (23) ноября 1842 г. Гаусс предложил Лобачевского как «одного из превосходнейших математиков русского государства» в члены Геттингенского ученого общества. Это общество уже тогда имело значение академии, это значение оно сохранило и впоследствии. Лобачевский был избран и получил диплом, подписанный Гауссом в качестве председателя общества и секретарем общества профессором И. Ф. Л. Гаусманом; последний еще несколько ранее уведомил Лобачевского о том, что он «в признание отличных научных заслуг» избран членом-корреспондентом общества. Это произошло вскоре после пожара в Казани, о котором сообщалось выше (стр. 283). Вследствие этого Лобачевский несколько запоздал ответом, который сохранился в бумагах Гаусса. «Выражаю желание, — пишет Лобачевский в своем ответе, — чтобы каждая из моих научных работ могла стоять на уровне превосходных работ Общества; во всяком случае приложу к этому все старания». Это, конечно, было для Лобачевского большим удовлетворением, единственным, которое он в жизни получил в связи со своим научным творчеством; удовлетворение немалое, потому что оно исходило от величайшего математика того времени. Но в печати Гаусс о своем отношении к работам Лобачевского не высказался, оставаясь верным установке, о которой нам придется говорить ниже8. О своем избрании Лобачевский доложил совету университета, по постановлению которого это внесено в его формулярный список. По существу, этим исчерпываются сочинения Лобачевского по геометрии; последняя работа «Пангеометрия», составленная Лобачевским в последний год его жизни, новых материалов уже не содержала. 1F. Еngеl. N. I. Lobatschefskij, cтp. 392. 2Л. Б. Модзалевский. Лобачевский, стр. 177. 3Там же, стр. 205. 4В. Я. Буняковский. Параллельные линии. Ученые записки Академии Наук, СПб., т. II, в. 3, 1853. 5См. об этом В. Каган. О преобразовании многогранников. 2-е изд., М. - Л., 1933. 6F. Еngеl. N. I. Lobatschefskij, сгр. 319. 7Sur la probabilite des resultats moyeus, tires des observations repetees. (О вероятности, средних результатов, полученных из повторных наблюдений.) 8Л. Б. Модзалевский высказывает убеждение, что личные сношения Лобачевского и Гаусса, «конечно, не ограничились указанной перепиской» (Л. Б. Модзалевский. Лобачевский, стр. 16). Уверен, что это не так. Гаусс о своих взглядах на вопросы об основаниях геометрии, — о них только и могла быть речь в переписке с Лобачевским, — писал исключительно самым близким своим друзьям с требованием сохранять их в полной тайне (см. ниже, стр. 377). Вряд ли ему удобно было ставить Лобачевскому такое требование. Лобачевский же при своей сдержанности и скромности вряд ли стал бы вызывать Гаусса на такое высказывание. Привет Гаусса Лобачевскому в письме к Симонову, на котором Л. Б. Моздалевский основывает свое мнение (Л. Б. Модзалевский, стр. 527), есть не более как новое выражение ему своего уважения, Все,что в наследии Гаусса относится к основаниям геометрии, в частности, к работам Лобачевского, воспроизведено в т. VIII собрания сочинений Гаусса. |
загрузка...
