XVII. Мемуар «О началах геометрии»
|
Многие ученые, одаренные большим талантом, отличались удивительной способностью соединять продуктивную научную работу с большой административной и общественной деятельностью. Лейбниц публиковал свои обширные философские и математические исследования среди большой государственной, административной и дипломатической работы. Монж соединял свою научную работу со сложными обязанностями по организации военного дела во время революционных войн. У нас М. В. Ломоносов также совмещал научную работу с большой административной деятельностью. Этим свойством обладал и Лобачевский. Когда подробно знакомишься с деятельностью Лобачевского в первый период управления университетом, даже когда читаешь только его письма к Мусину-Пушкину, то недоумеваешь, как он мог совместить с этими сложными обязанностями углубленную исследовательскую работу. Между тем именно в эти годы он опубликовал самые важные свои труды.
Мы уже знаем, что в 1829 г. в «Казанском вестнике» был напечатан первый его мемуар «О началах геометрии»1. Это первая и в то же время самая важная из всех опубликованных работ Лобачевского; она содержит все основные его идеи и методы, которые он в дальнейших своих работах подробно развертывает. Мемуар четко разделяется на три части. Первая часть имеет целью обосновать самые исходные начала общей (как теперь говорят, абсолютной) геометрии. По существу, это изложение тех же идей, которые выявлены уже в «Геометрии» 1823 года. Они изложены здесь чрезвычайно кратко — на четырех-пяти страницах; подробное их развитие содержится в обширном сочинении Лобачевского «Новые начала геометрии с полной теорией параллельных». При изложении его содержания в XXI главе настоящей книги мы остановимся на них более подробно. Вторая часть мемуара «О началах геометрии» восстанавливает доклад Лобачевского «Exposition succincte» и содержит изложение начал «воображаемой» неевклидовой геометрии, заканчиваясь уравнениями, связывающими стороны и углы прямолинейного прямоугольного треугольника. Как мы видели, Лобачевский прежде всего ставит вопрос о значении постоянной q в уравнениях (8) и (12), определяющей функцию П(х) (стр. 202). Он предпочитает, впрочем, пользоваться другой, связанной с q константой k, представляющей число, обратное натуральному логарифму q, так что 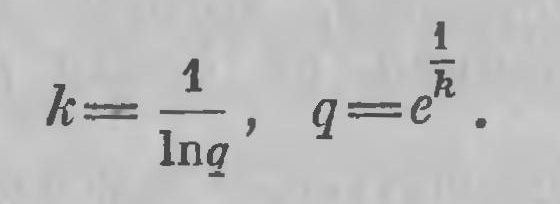 (13) (13)
Евклидова геометрия "соответствует значению q — 1, т. е. значению к = v. Уравнение же (12) принимает вид: 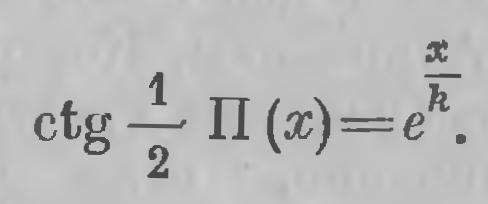 (14) (14)
Дальнейшие рассуждения исходят из того факта, что угол параллельности П(х) неограниченно приближается к d (к прямому углу), когда х стремится к нулю. Иными словами, как бы мал ни был угол α, при достаточно малых значениях х угол П(х) отличается от d меньше чем на α. Сопоставим теперь два обстоятельства: 1) геометрический факт, что в евклидовой геометрии угол, параллельности всегда прямой; 2) чисто физический факт, что всякий прибор, в том числе, конечно, и угломерный, имеет предел чувствительности. В эпоху Лобачевского чувствительность угломерных приборов едва достигала 1"; это значит, что углы, различающиеся менее чем на 1", измерительными приборами не могли быть отличены один от другого. Сделаем теперь предположение, что в нашем пространстве имеет место не обыкновенная геометрия Евклида, а «воображаемая» геометрия Лобачевского. Обозначим через z расстояние, при котором угол параллельности в нашем пространство отличается от d меньше чем на 1". Если бы мы производили измерения углов параллельности на расстояниях, меньших z, то мы не отличали бы их от прямого угла; мы имели бы впечатление, что в пространстве, в котором мы оперируем, царит геометрия Евклида. Такое положение должно было бы наступить неизбежно, если бы мы ограничили круг своих наблюдений достаточно малой областью. Но какую область мы должны считать малой? Каково то расстояние z, на котором угол параллельности отличается от прямого меньше чем на 1"? Теория не дает, не может дать на это никаких указаний. Не лишено возможности, что при огромных размерах вселенной те расстояния, которые мы считаем большими, даже расстояния от Земли до звезд, все еще меньше этого z. «Нельзя не увлекаться,— замечает Лобачевский,— мнением Лапласа, что видимые нами звезды принадлежат к одному только собранию небесных светил, подобно тем, которые усматриваем как слабо мерцающие пятна в созвездиях Ориона, Андромеды, Козерога и др. Итак, не говоря о том, что в воображении пространство может быть продолжено неограниченно, сама природа указывает нам такие расстояния, в сравнении с которыми исчезают за малостью даже и расстояния нашей Земли до неподвижных звезд». Между тем, после Лобачевского за истекшие сто с лишком лет обнаружено, что космические расстояния, доступные нашему измерению, несравненно больше, чем себе рисовал Лаплас; расстояния между звездами иногда выражаются в сотнях миллионов световых лет. И становится совершенно естественным думать, что наша вера в незыблемую точность евклидовой геометрии имеет свой источник в том обстоятельстве, что все наши измерения и наблюдения производятся в совершенно ничтожном, «исчезающем», по выражению Лобачевского, уголке вселенной. Как же это выяснить? Попытку опытной проверки того, имеет ли в нашем пространстве место, как выражается Лобачевский, «употребительная или же воображаемая геометрия», он делал, исходя из другого принципа. Мы знаем уже, что дилемма между евклидовой и неевклидовой геометрией Лобачевского эквивалентна тому, равна ли сумма внутренних углов прямолинейного треугольника 2d или она меньше 2d. Это Лобачевский и хотел экспериментально проверить. С этой целью, опираясь на значения параллаксов трех неподвижных звезд (по его номенклатуре—Кейды, Ригеля и Сириуса), Лобачевский вычисляет сумму углов в треугольнике, вершины которого находятся в Земле, в Солнце и в одной из этих звезд. В частности, выполнив вычисления для того случая, когда третьей вершиной треугольника служит Сириус, он приходит к выводу, что эта сумма отличается от 2d меньше чем на 0.000372". Нужно, однако, сказать, что самое это вычисление представляет значительные трудности. Дело в том, что параллаксы, которыми приходится пользоваться, рассчитаны средствами евклидовой геометрии, и возникает вопрос, в какой мере допустимо пользоваться этими значениями в тех вычислениях, которые Лобачевский предпринимает. Он придумал для этого обходный путь, с обоснования которого он и начинает свои вычисления2. В вычисления Лобачевского вкралась ошибка: разница получается еще в 100 раз меньшей. Само собой разумеется, что этот результат не может служить основанием для решения вопроса при учете размеров вселенной; некоторые конкретные основания для этого, притом все еще очень ненадежные, заставили себя ждать около 100 лет. Но принципиально вера в незыблемость евклидовой геометрии уже была подорвана, правда, в то время еще у очень немногих математиков, которые были в состоянии усвоить идеи Лобачевского, которые были способны отрешиться от беспросветной косности, всегда стоявшей на пути смелой научной мысли. Не будем, однако, забегать вперед, возвратимся к вопросу о константе k. Заметим прежде всего, что уравнение (14) дает 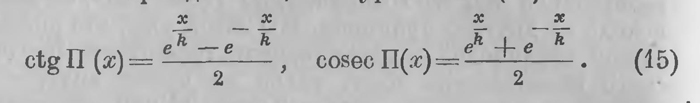
Если правые части разложим в ряды по степеням x/k считая эту дробь весьма малой, сохраним только члены порядка ниже 3-го, то получим 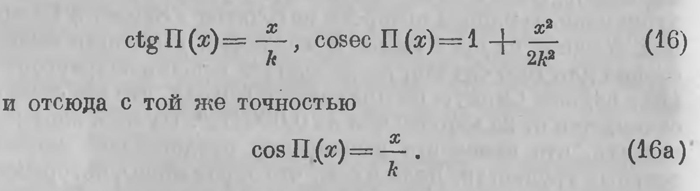
Можно сказать, что функции ctg П(х), cosec П(х) и сов П(х) имеют эти значения (16) и (16а) для значений х, настолько малых по сравнению с k, что третьей степенью отношения x/k можно пренебречь. Вставив эти значения в уравнения (11) (стр. 200), получим: а = с sin A, b = c sin B, а2 + b2 = с2; мы приходим к уравнениям евклидовой геометрии. Итак, каково бы ни было значение k, на протяжениях, весьма малых по отношению к k, действуют соотношения евклидовой геометрии; это уточняет соображения, уже высказанные выше. В связи с этим Лобачевский приходит к убеждению, что теоретически к может иметь совершенно произвольное значение; это значит, каждому значению константы к соответствует своя логически безукоризненно правильная «воображаемая» геометрия. Иначе говоря, существует не одна «воображаемая» геометрия; она допускает бесконечное множество разновидностей, соответствующих различным значениям постоянной (параметра) k. Среди них предельное место (при к = ∞) занимает старая геометрия Евклида. Что касается того, какое значение имеет к в нашем конкретном пространстве, в котором прямыми линиями служат лучи света, то это вопрос не логический, а физический; установить это возможно только экспериментально. Пока наши измерения не дают никаких отклонений от геометрии Евклида, мы можем предполагать, что она только и существует в нашем пространстве. Но если бы измерения наши, проникнув в очень удаленные области мироздания, обнаружили отклонения от геометрии Евклида, то по характеру и размерам этого отклонения можно было бы определить значения константы k. Однако каково бы ни было значение постоянной k, соответствующая неевклидова геометрия имеет своеобразную особенность; в ней каждому отрезку соответствует некоторый угол (угол параллельности, отвечающий этому отрезку), и обратно, каждому углу соответствует некоторый отрезок (отрезок параллельности, отвечающий этому углу); имеет место некоторая зависимость между отрезком и углом. До Лобачевского геометры, пытавшиеся доказать постулат о параллельных от противного, неоднократно приходили к заключению, что отрицание постулата приводит к «неестественной зависимости» между отрезком и углом. Это особенно подчеркивал Лежандр, дававший этому такое выражение, что отрицание V постулата нарушает принцип однородности,— это и есть тот абсурд, к которому такое отрицание приводит. Лежандр так понимает сущность этого «принципа». Положим, что каждому углу ω отвечает некоторый отрезок x, иначе говоря, отрезок х есть функция угла ω:х=ω(x). Между тем угол, как обыкновенно говорили, выражается отвлеченным числом; следовательно, и ω(x) есть число отвлеченное; с левой же стороны предыдущего равенства стоит «линейная величина» х. Принцип однородности заключается в том, что такое равенство невозможно. Это мотивируется так: если изменим единицу длины, то правая часть от этого не изменится, левая же приобретет некоторый множитель; равенство нарушится, оно не может иметь места. Принцип однородности, таким образом, приводит к доказательству постулата. Но уравнение (14) показывает, что угол определяется не отрезком, а отношением отрезка к другому постоянному отрезку длины k. Однородность вовсе не нарушается; неожиданно только то, что выплывает константа — постоянный отрезок. Приведем теперь подлинные слова Лобачевского: «После этого нельзя утверждать более, что предположение, будто мера линий не зависит от углов, предположение, которое многие геометры хотели принимать за строгую истину, не требующую доказательства, может быть оказалось бы приметно ложным еще прежде, нежели перейдем за пределы видимого нами мира. С другой стороны, мы не в состоянии постигать, какая бы связь могла существовать в природе вещей, и соединять в ней величины столь разнородные, каковы линии и углы. Итак, очень вероятно, что евклидовы положения одни только истинные, хотя и останутся навсегда недоказанными. Как бы то ни было, новая геометрия, основание которой уже здесь положено, если и не существует в природе, тем не менее может существовать в нашем воображении, и, оставаясь без употребления для измерений на самом деле, открывает новое обширное поле для взаимных применений геометрии и аналитики». Конечно, это утверждение еще звучит недостаточно убедительно. Не было уверенности, что в построении Лобачевского, по-видимому складном в своих элементах, где-либо не таится противоречие, что новая геометрия, даже если она только и «существует в нашем воображении», остается безукоризненно правильной и притом при любом значении k, что она действительно открывает надежный путь «для взаимных приложений геометрии и аналитики». Лобачевский это хорошо понимал; это, главным образом, и побудило его к дальнейшему развитию воображаемой геометрии. Такое развитие идет через аналитическую и дифференциальную геометрию неевклидова пространства. Лобачевский дает их развитие в мемуаре «О началах геометрии». Допуская существование новой геометрии при любом значении параметра k, Лобачевский принимает отрезок длины к за единицу меры. Это, не нарушая общности, приводит к упрощению формул и вычислений; так, формулы (14) — (16) принимают вид 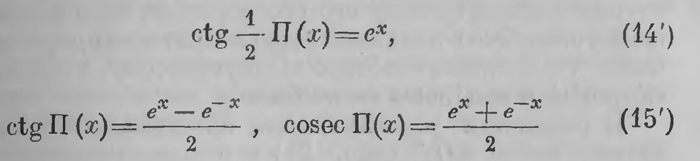
и для отрезков весьма малых по сравнению с принятой единицей ctg П(x)=x, cosec П(x) = 1x2/2 , cos П(x) = x. (16') При всем том, и это наводило на серьезные сомнения и возражения. Выходит, что в пространстве, в котором имела бы место геометрия Лобачевского, должна была бы существовать некоторая определенная длина, определенный стандартный отрезок, который преимущественно надлежало бы принять за единицу меры; выходит, что можно принципиально отличать один отрезок от другого. Единицу меры длины в евклидовом пространстве можно определить только непосредственным физическим заданием соответствующего отрезка — эталоном; это физическое задание единицы длины. В пространстве Лобачевского мы можем задать единицу длины, например, таким положением: примем за единицу длины отрезок, которому соответствует угол параллельности в 45°. Этим единица длины будет задана геометрически. «Нельзя себе представить,— говорили,— каким образом один отрезок может быть геометрически, словесным определением отличен от Других». Даже Гаусс по этому поводу писал: «Единственно, что в этой системе противится нашему разуму, это то, Что в пространстве, если бы эта система была справедлива, должна была бы существовать некоторая определенная (хотя нам и неизвестная) линейная величина. Но мне кажется, что мы, кроме ничего не выражающей словесной мудрости метафизиков, знаем очень мало или даже не знаем ничего о сущности пространства». Отметив, однако, эти соображения, возвратимся к вычислениям Лобачевского, к построению аналитической и дифференциальной геометрии в общей системе его своеобразной «воображаемой» геометрии. Это составляет третью часть мемуара «О началах геометрии», особенно важную потому, что в докладе «Exposition succincte» ее не было. В плоскости устанавливаем ортогональный координатный крест XOY (рис. 21) и из произвольной точки 
плоскости опускаем па прямые ОХ и OY перпендикуляры MN и MN'. Как и в классической геометрии, принимаем длины отрезков ON и NM, взятые с надлежащими знаками, за абсциссу и ординату (х и у) точки М. Нужно, однако, иметь в виду, следующее. Здесь, в плоскости Лобачевского, четырехугольник MNON1 имеет только три прямых угла; угол при вершине М—острый. Вместе с тем отрезки NM и ON' не равны между собой, неравны также и отрезки ON и N'М. Таким образом, ордината у не может быть заменена длиной отрезка ON1; если бы за ординату принять длину ON', то это была бы уже другая координация. Длины отрезков ON’ и N'М обозначим соответственно через у' и х'; тогда х’>х, у>у'- Это следует из того, что прямые NM и ON' расходятся по мере удаления от общего перпендикуляра ON, прямые N'M и ON расходятся по мере удаления от общего перпендикуляра ON'. Аналитически же это вытекает из соотношений, связывающих эти четыре отрезка; эти простые соотношения нам понадобятся, мы их выведем. Как для этих, так и для последующих вычислений необходимо только усвоить тригонометрические уравнения (11а) — (11е). По теореме косинусов (11е) из прямоугольного треугольника MN'O следует 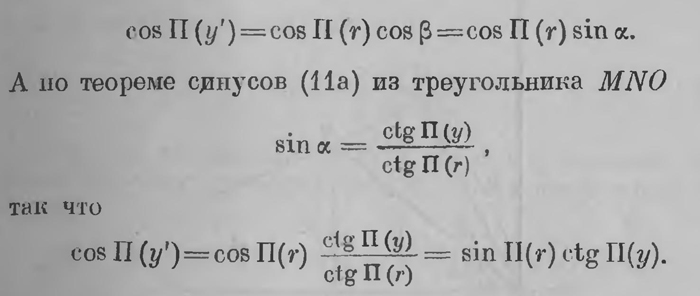
А так как в силу соотношения между катетами и гипотенузой прямоугольного треугольника (11с) sin П (r) = sin П (x) sin П (у), (17) то предыдущее равенство примет вид: cos П (y') = cos П (у) sin П (x). (18) Отсюда ясно, что соs П (у') < cos (у), П (у’) > П (у), у' < у. (19а) Аналогично этому найдем, что cos П (х) = cos П (х') sin П [у'), х' > х. (19b) Таким образом пары чисел (х, у), (х, у'), (у, х’), (у'х') представляют в плоскости Лобачевского существенно различные координаты точки. Начала аналитической геометрии — выводы уравнений простейших линий — опираются на тригонометрические соотношения. Мы дадим здесь эти выводы, чтобы ввести читателя, который этим интересуется, в вычисления и рассуждения Лобачевского. Это существенно важно не только для того, чтобы несколько расширить свои сведения из неевклидовой геометрии, но и для уяснения того развития, которое идеи Лобачевского получили в дальнейшем. 
Тот же треугольник MNO (рис. 21) (теорема тангенсов (lid)) дает: cos П (y) = ctg П (x) tgα. (20) Это — уравнение прямой, проходящей через начало координат под углом а к оси абсцисс. Но нетрудно вывести и общее уравнение прямой. Положение прямой определяется длиной р опущенного на нее из начала перпендикуляра ОР (рис. 22) и углом ω, который он образует с осью абсцисс. Длину радиуса-вектора произвольной точки М прямой обозначим через r, углы, на которые он делит угол ω, обозначим через α и β. Прямоугольный треугольник МОР по теореме косинусов (уравнение (Не)) дает cos П (р) = cos П (r) cos β = cos П (r) cos (ω — α) = cos П (r) cos α cos ω + cos П (r) sin α sin ω. (21) Но в силу той же теоремы косинусов (Не) из треугольника MON следует, что cos П (r) cos α = cos П (x); (22a) в силу же теоремы синусов (11а) 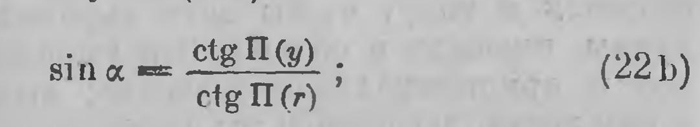
подставляя выражения (22а) и (22Ь) в уравнение (21), после простого преобразования в последнем члене получи м: cos П (р) = cos П (х) cos ω + sin П (r) ctg П (у) sin ω. В силу же соотношения (17) получаем окончательно cos П (р) = cos П (x)cos ω+ sin П (x) cos П (y) sin ω. (23) Это и есть общее уравнение прямой в плоскости Лобачевского в декартовых координатах (х, у). Как видно, оно имеет довольно сложный вид, трансцендентный характер; это обусловливается тем, что декартовы координаты здесь не являются наиболее простыми, даже не являются наиболее подходящими для составления уравнения прямой. Это уравнение получает более простой вид, если пользоваться координатами х и у'. В самом деле, в силу соотношения (18) оно принимает вид cos П(x) cosω+ cos П(у') sinω = cos П(p). (23а) Казалось бы, здесь напрашивается дальнейшее упрощение; но от Лобачевского оно ускользнуло и выплыло нескоро. Еще проще выводится уравнение окружности. Ограничиваясь случаем, когда центром окружности служит начало координат, видим, что тот же прямоугольный треугольник MON приводит для окружности радиуса r к уравнению (17). Лобачевский выводит также уравнение предельной линии. Вслед за этим Лобачевский переходит к измерению длин, площадей и объемов. Так как эти вычисления выполняются путем интегрирования, то задача прежде всего сводится к тому, чтобы дать выражения для элементов длины, площади и объема. Эти выражения имеют основное и принципиальное значение; вычисления, которые к ним ведут, несложны; мы дадим здесь их выводы. Предварительно приведем очень характерные вступительные слова Лобачевского к учению об измерении длин: «Кривая линия не может быть составлена из прямых, а потому измерение кривой помощи прямой дает только условную величину, за которую обыкновенно принимают границу приближения, когда соединяют прямыми точки на кривой, ближе и ближе друг от друга взятые. Легко видеть, какая цель предположена с таким исчислением. Кривые линии измеряются на самом деле помощи цепи, которая, почитают, тем вернее определяет величину кривой, чем звенья менее, так что гибкая нить дает уже эту величину без приметной погрешности. Надобно, следовательно, доказывать только, что граница приближения существует, потом показать, каким образом ее отыскивать». Немного слов нужно прибавить для того, чтобы это определение длины кривой удовлетворило современного математика. Обращаемся теперь к вычислению элемента (дифференциала) длины кривой. Лобачевский рассматривает, как это делалось в обыкновенной геометрии, две весьма близкие точки кривой А и А' (рис. 23) и исходит из того, что отношение длины дуги А А' к длине ее хорды по самому определению длины кривой стремится к 1, когда та и другая стремятся к нулю. Теперь проектируем точки А (х, у) и А' (я + dx, у + dy) на ось абсцисс перпендикулярами АВ и А'В'. Приращение ВВ' абсциссы обозначаем через dx. Откладываем на В 'А1 отрезок В' С = В А, так что отрезок С А' дает соответствующее приращение ординаты dy; отрезок же АС обозначим через dx'. Четырехугольник АВВ'С существенно отличается от прямоугольника евклидовой плоскости. Углы при основании ВВ' прямые, но при основании АС они острые, ибо они равны, а сумма их меньше 2d. Вместе с тем dx'>dx, ибо перпендикуляры АВ и А'В' к оси абсцисс расходятся по мере 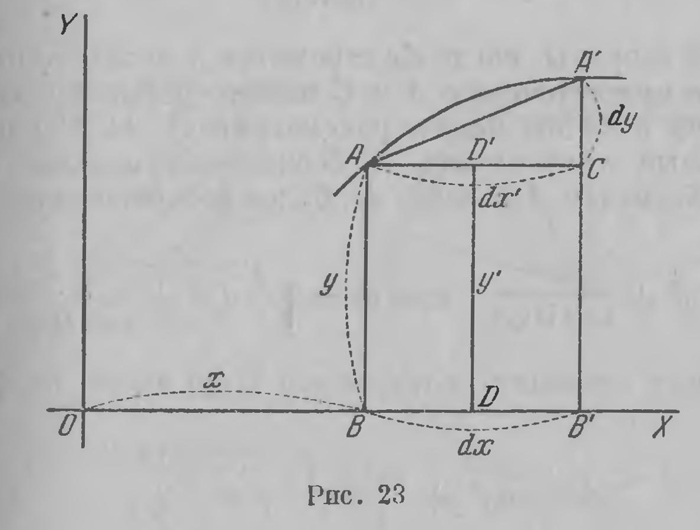
Удаления от нее. Если соединим середины D и D' основании ВВ' и АС этого четырехугольника, то легко усмотреть, что прямая DD' перпендикулярна как к ВВ', так и к С А. Вместе с тем четырехугольник DD'CB' по своему строению не отличается от четырехугольника ON'MN на рис. 21; отрезки DB' =^dx uD'C =у dx' здесь заменяют х и х' рис. 21. Соотношение (19Ь) поэтому дает: cos П(1/2dx) = cos П(1/2dx') sin П(у'), где у' есть отрезок DD'. Но поскольку отрезки dx и dx' бесконечно малы, гредыцущее соотношение в силу приближенных значений (16а) принимает вид dx=dx' sin П (у'). Если отрезок Устремится к нулю, то у' явно стремится к у, и отношение dx': dx стремится к пределу 1/sin П (у). Поэтому с точностью до бесконечно малых второго порядка 
С другой стороны, когда dx стремится к нулю, то каждый из углов при вершинах А и С нашего четырехугольника стремится к d. Мы можем рассматривать АСА' как прямоугольный треугольник с бесконечно малыми сторонами. Обозначая А А' через dх, будем соответственно этому иметь 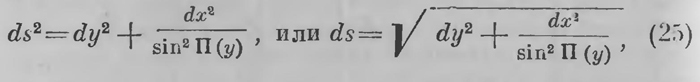
или в силу значения, которое sin П (у) имеет по формуле (15), 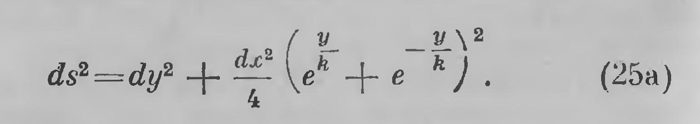
Дифференциальная форма (25) представляет собой явное обобщение основной метрической формы евклидовой плоскости. В самом деле, в евклидовой геометрии П{y)=d, и предыдущая форма (25) принимает вид, который метрическая форма имеет в классической геометрии, dx2=dx2 + dy2. Из основной формы (25), конечно, должна развертываться вся метрическая геометрия плоскости. Лобачевский пользуется ею прежде всего для вычисления длины окружности. Он преобразовывает для этого выражение (25) К полярным координатам r, ω; мы без труда разыщем соответствующее выражение ds2 непосредственно. Пусть те же точки А и А' имеют полярные координаты r, ω и r+ dr, ω+dω (рис. 23'). Если окружность, имеющая центр в точке О и радиус r, пересекает радиус-вектор О А' в точке В, то мы можем считать, что АВА' есть прямолинейный бесконечно малый треугольник с прямым углом при вершине В. Поэтому до бесконечно малых выше 2-го порядка 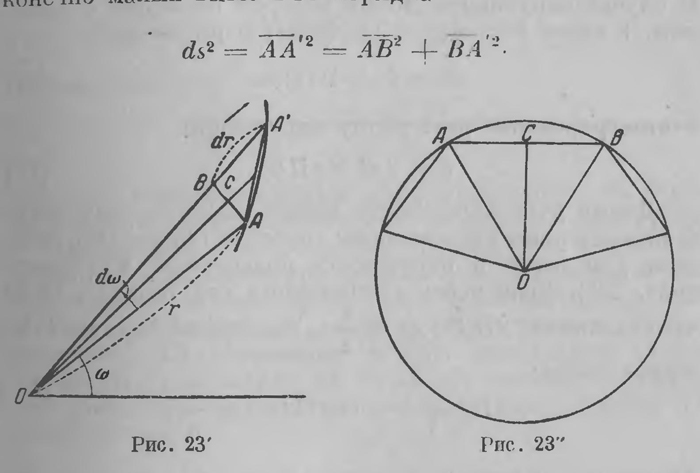
Но ВА' = dr; чтобы вычислить катет АВ (который также можно считать прямолинейным), проводим биссектрису ОС угла АОВ. Если длину отрезка АВ обозначим через u (u = АВ), то из прямоугольного треугольника АОС во формуле (11а) получим: 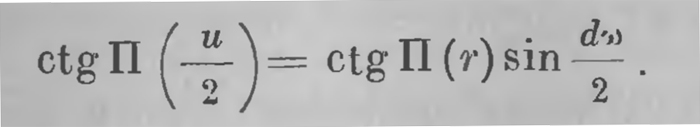
с другой стороны, так как отрезок u и угол dω бесконечно малы, то мы можем с той же степенью точности по формуле (16) заменить ctg П (u/2) через u/2k, a sin dω/2 через dω/2 получим: АВ = u = k ctg П (r) dω, а вместе с тем ds2 = dr2+k2 ctg2 П (r) dω2. (26) В случае окружности, центр которой совпадает с началом, г имеет постоянное значение; формула дает ds = k ctg П (r) ω, (27) а интегрирование дает длину окружности с = 2 πk ctg П (r). (28) Длину дуги окружности можно, конечно, вычислить и элементарным классическим способом (Архимеда). Впишем для этого в окружность правильный n-угольник (рис. 23"). Если через аn обозначим его сторону, то из треугольника АОС (АС = 1/2аn) по той же формуле (11а) будем иметь: 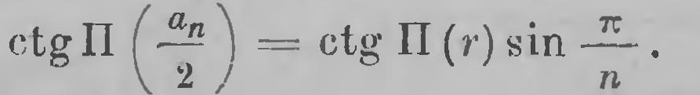
Обозначая периметр многоугольника nаn через рn, можем это равенство написать в виде: 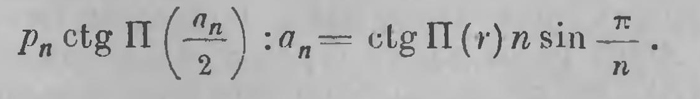
Если n неограниченно возрастает, то ln имеет своим пределом длину окружности с, отношение ctg П(аn/2):аn по формуле (16) имеет пределом 1/2k, a n sin π/n стремится к π. Заменяя переменные их пределами, мы вновь получим формулу (28). Если дуга окружности имеет центральный угол 2α, то длину s этой дуги получим, умножая выражение (28) α/π s = 2αk ctg П (r). Обозначим через 2l хорду этой дуги. Тогда всё по той же формуле (11а) из прямоугольного треугольника АОС получим: 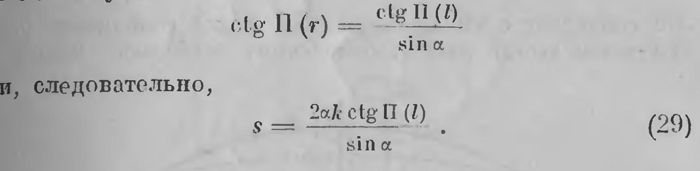
Это есть выражение длины дуги окружности по длине ее хорды и опирающемуся на нее центральному углу. Представим себе теперь, что концы А и В дуги АВ остаются неподвижными, а центр проходящей через них окружности удаляется от С по перпендикуляру СО. Угол а уменьшается и, когда центр О уходит в бесконечность, АВ обращается в дугу предельной линии, имеющую ту же хорду АВ — 2l. Мы поэтому получаем, что длина S предельной дуги, опирающейся на хорду 2l, имеет значение S = 2kctgП(l). (29а) Отсюда вытекают два вывода. Во-первых, если П(l) = π/4, то k = 1/2S. Постоянная k есть половина длины предельной дуги, полу хорде которой соответствует угол параллельности, равный половине прямого угла. Во-вторых, если предельная линия АСВ вращается вокруг диаметра СО, то она описывает предельную поверхность. Точки А и В описывают окружность, которая имеет прямолинейный радиус r = l но ее можно рассматривать также как окружность на предельной поверхности c центром в точке С и геодезическим радиусом 1/2S (рис. 24). А так как на предельной поверхности имеет место геометрия Евклида, то длина этой окружности c = 2π1/2S = 2πk ctg П (r). Это совпадает с выражением (28). Такое совпадение результатов всегда дает Лобачевскому особенное удовлетворение, так как утверждает его в убеждении ло1ическоп правильности построенной им геометрии. 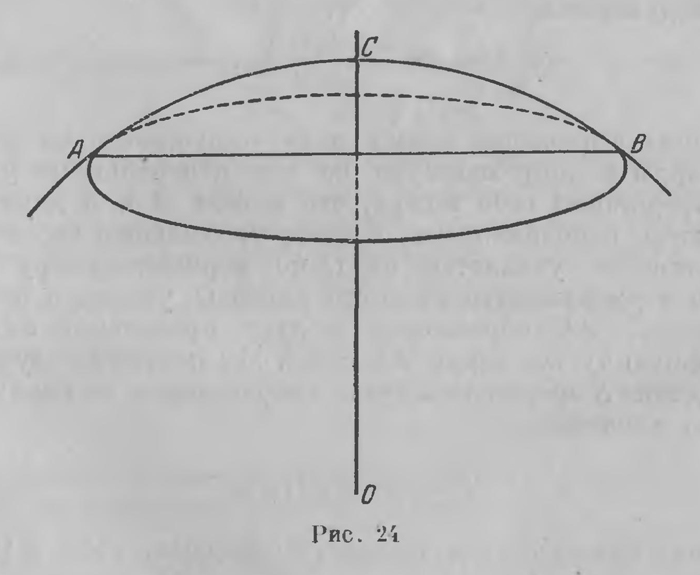
Следующий шаг заключается в вычислении элемента dσ площади. Принимая за таковой площадку (рис. 25), соответствующую наращению абсциссы на dx и ординаты на dy, Лобачевгкий исходит из того, что эту площадку можно рассматривать как прямоугольник в евклидовой плоскости со сторонами dx' и dy; ее площадь dσ равна поэтому dx'dy, а вследствие соотношения (24) 
двойное интегрирование в надлежащих пределах дает тыражение площади измеряемой фигуры. И эта формула совпадает с евклидовой при П(у) = π/2. Лобачевский с большим искусством выполняет интегрирование выражения (30) 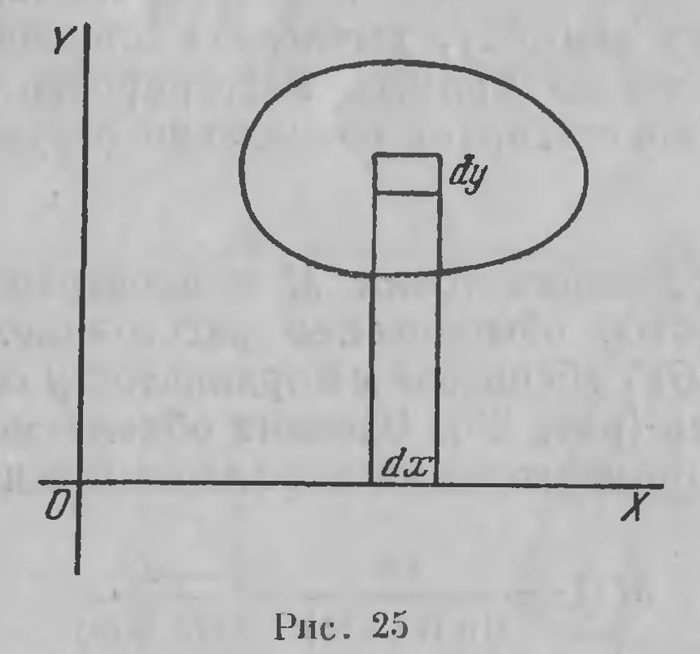
прежде всего в применении к треугольнику и приходит к заключению, что площадь треугольника пропорциональна угловому дефекту, т. е. разности между π и суммой углов треугольника; при надлежащем выборе единицы площади она выражается непосредственно этой разностью. Затем Лобачевский показывает, что к этому результату можно прийти элементарными синтетическими рассуждениями, и вновь констатирует совпадение результатов3. Разбивая многоугольник на треугольники, легко получить, что площадь многоугольника пропорциональна его угловому дефекту, т. е. разности 2d (n — 2) — S, (31) где S — сумма внутренних его углов; площадь непосредственно выражается этой разностью при надлежащем выборе единицы для измерения площадей. Располагая выражением для площади многоугольника, можно, следуя обычному замыслу, вычислить площадь круга. Выполняя это также прямым интегрированием, Лобачевский вновь констатирует совпадение результатов. Для координации точки М в пространстве Лобачевский пользуется обыкновенно расстоянием z точки от плоскости XOY, абсциссой х и ординатой у ее проекции на эту плоскость (рис. 26). Элемент объема можно рассматривать как прямоугольный параллелепипед со сторонами ММ' =dz, 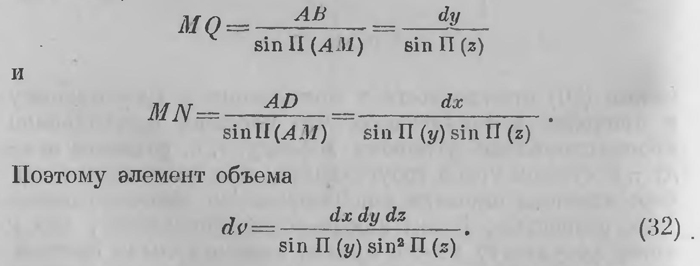
Нет нужды подчеркивать, что при П (у) = П (z) = d формула переходит в обыкновенное евклидово выражение элемента объема. Выражение элемента объема Лобачевский приспособляет для вычисления объемов тел вращения; он находит следующее выражение для объема круглого конуса: v=π(l cos С — h), (33) где l — образующая, h — высота конуса, а С — угол между высотой и образующей. Если из круглого конуса возьмем вырезок (рис. 27), который высекается двумя плоскостями, проходящими через ось и образующими угол ω, то его объем получим, умножая выражение (33) на ω/2π v = ω/2{l cos С — h). (33а) Предполагается, что угол ω выражен в единицах, в которых прямой угол выражается числом π/2. 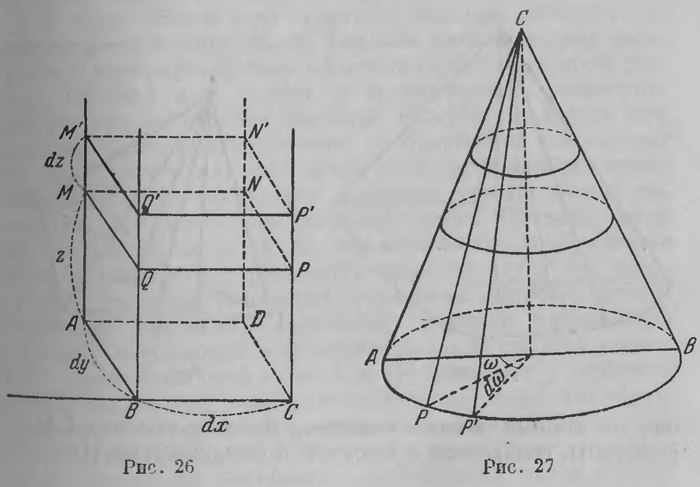
Это дает возможность вычислить объем любого конуса. Если через перпендикуляр, опущенный из вершины на плоскость основания, будем проводить плоскости и через ω будем обозначать азимут, отсчитываемый от одной из этих плоскостей (рис. 28), то l и С будут функциями от ω. Объем бесконечно малого вырезка будет иметь значение 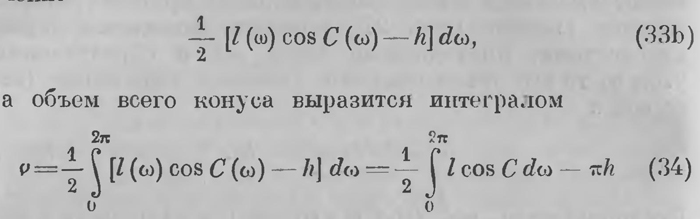
(в предположении, что высота падает внутрь конуса). Однако это выражение отнюдь не столь простое, каким 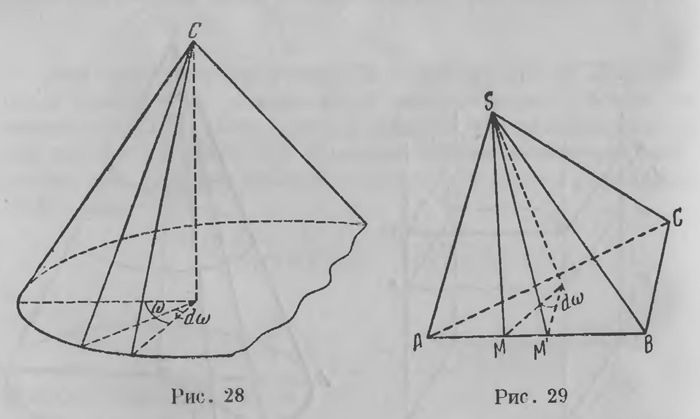
оно на первый взгляд кажется. Дело в том, что l C — величины, связанные с высотой h зависимостью (11е) соs П (h) = cos П (l) cos С. (35) Если формулу (34) выразить только через С и l, как это во многих случаях необходимо, или через С и h, то она значительно усложнится. На всякую пирамиду можно также смотреть как на конус с переменными значениями l и С, зависящими от ω. руководясь этим, Лобачевский вычисляет объем любой пирамиды, рассматривая ее как конус, основанием которого служит многоугольник, в частности треугольник, если речь идет о тетраэдре (рис. 29). В последнем случае, в зависимости от выбора основания, мы получаем для объема тетраэдра различные интегральные выражения; иногда тот или иной из этих интегралов поддается вычислению; и тогда этим определяются значения остальных интегралов, выражающих тот же объем. Если ни один из интегралов не раскрывается, то мы приходим к различным интегралам, имеющим то же значение; мы получаем формулы, иногда очень интересные, для преобразования одного интеграла в другой. В более общем виде основной замысел Лобачевского заключается в следующем. Тот или иной интеграл часто удается интерпретировать в виде значения некоторой длины, площади или объема в воображаемой геометрии. Между тем иногда это значение удается разыскать при помощи чисто геометрических соображений, основанных на новой геометрии; этим путем средствами воображаемой геометрии устанавливается значение определенного интеграла. Но более того, нередко, когда значение интеграла уже найдено, те же геометрические соображения дают указания, как разыскать значение этого же интеграла чисто аналитическими средствами. Получается возможность проверить результат, который найден при помощи соображений, основанных на неевклидовой геометрии. Совпадение результатов часто вызывает у Лобачевского, как говорит один из его комментаторов4, «наивную радость по поводу подтверждения правильности его геометрии, завоеванного путем сложных вычислений». К такому же результату Лобачевский часто приходит, выражая интеграл, имеющий то или иное геометрическое значение, в различных координатах. Методы координации, как мы уже имели случай видеть, в неевклидовой геометрии особенно многообразны; переходя от одной координации к другой, Лобачевский иногда находит значение сложного определенного интеграла, иногда приводит одни интегралы к другим. Он дает таким образом приложение воображаемой геометрии к анализу. Мемуар заканчивается таблицей, содержащей «сравнение интегралов и найденные вновь определенные интегралы». Впрочем, в самом заключении Лобачевский отмечает еще один очень важный факт. Уравнения тригонометрии (11а) — (11с) можно, пользуясь выражениями (15) тригонометрических функций от угла П (х), записать в таком виде: 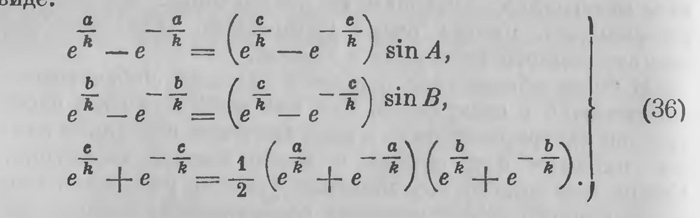
Сопоставим их с уравнениями сферической тригонометрии, — точнее, с уравнениями, связывающими катеты а, Ь, гипотезу с и острые углы А, В прямоугольного сферического треугольника, т. е. с уравнениями (10а)—(10с). В них под а, Ь и с нужно разуметь угловые значения сторон сферического треугольника; если а, Ь и с означают длины этих сторон, то в тех же уравнениях нужно а, Ь, с заменить через а/r, Ь/r и с/r где r — радиус сферы; если, сверх того, выразим тригонометрические функции при помощи известных формул Эйлера, то представим уравнения прямоугольного сферического треугольника в виде: 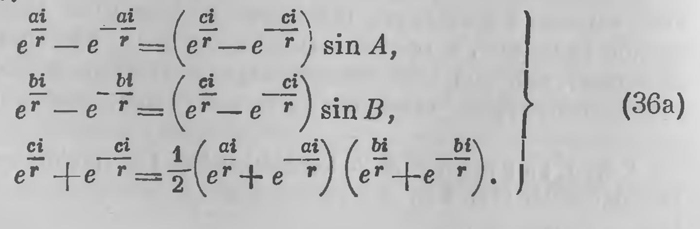
Сличая уравнения (36) и (36а), видим, что первые получаются из последних, если в них заменить r через ki. Тригонометрические уравнения геометрии Лобачевского получаются из уравнений сферической геометрии заменой радиуса сферы r через ki. Планиметрия Лобачевского формально может быть рассматриваема как геометрия мнимой сферы. Тот же факт можно выразить еще следующим образом. Уравнения сферического прямоугольного треугольника (36а) выражены в тригонометрических функциях сторон; уравнения прямолинейного прямоугольного треугольника в геометрии Лобачевского выражаются в соответственных гиперболических функциях. Уравнения (36) и (36а) могут быть написаны в таком виде: 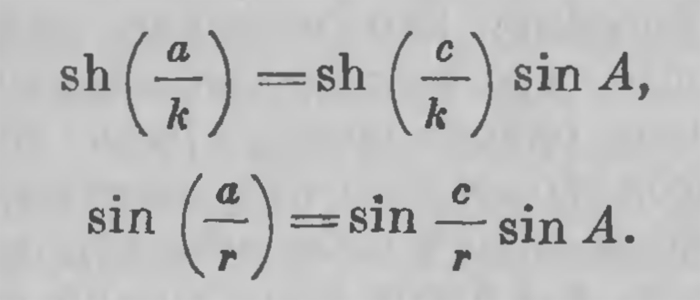
Это обстоятельство послужило основанием тому, что гео“ метрик» Лобачевского стали называть гипербол и“ ческой геометрией. Совокупность всех установленных Лобачевским фактов уже исключала в его глазах возможность возникновения какого-либо противоречия в открытой им геометрии. Вот как он сам выражает эту мысль в заключении мемуара: «После того, как мы нашли уравнения (17)5, которые представляют зависимость углов и боков треугольника; когда, наконец, дали мы общие выражения для элементов линий, площадей и объема тел, все прочее в геометрии будет уже аналитикой, где исчисления необходимо должны быть согласны между собой и ничего не в состоянии открыть нам нового, чего бы не заключалось в тех первых Уравнениях, откуда должны быть взяты все отношения геометрических величин друг к другу; итак, если надобно предполагать теперь, что какое-нибудь противоречие принудит впоследствии опровергнуть начала, принятые нами в этой новой геометрии, то это противоречие может только скрываться в самых уравнениях (17). Заметим, однако, что эти уравнения переменяются в (20)6 сферической тригонометрии, как скоро, вместо боков а, Ь, с, ставим   ; но в обыкновенной геометрии и в сферической тригонометрии везде входят одни содержания линий; следовательно, обыкновенная геометрия, тригонометрия и эта новая геометрия всегда будут согласны между собой. ; но в обыкновенной геометрии и в сферической тригонометрии везде входят одни содержания линий; следовательно, обыкновенная геометрия, тригонометрия и эта новая геометрия всегда будут согласны между собой.
Если теперь аналитика с новой — назовем воображаемой геометрией, в отличие от употребительной — соглашены уже между собою, то можно ожидать от той и другой взаимного пособия. Это ожидание кажется не без основания, и после того как предположивши собственно достигнуть только одной цели — дать общие правила для измерения всех геометрических величин, — идя прямо к этой цели и дозволивши себе мимоходом только некоторые применения, мы были в состоянии открыть значения определенных интегралов, к познанию которых одной аналитике, без пособия геометрии, трудно было бы проложить дорогу». Итак, мемуар «О началах геометрии» содержит не только основы новой геометрии, которые нашли себе место уже в «Exposition succincte», но и далеко идущее ее развитие: начала аналитической геометрии и метрики, устанавливаемой инфинитезимальными средствами. По существу, к этому уже немного оставалось прибавить. Мемуар содержит также приложения новой геометрии к разысканию определенных интегралов и вычисления, имеющие главной своей целью подтвердить логическую правильность этой геометрии. Была создана новая наука, охватывающая все вопросы метрической геометрии; старая же геометрия Евклида вошла в эту геометрию как простейший частный, можно сказать, как предельный ее случай. 1Точнее, мемуар был напечатан частями, в книжках за февраль, март, апрель и ноябрь, декабрь 1826 г. и в книжках за март, апрель и июль, август 1830 г. 2Эти рассуждения Лобачевского можно найти в томе I «Полного собрания сочинений» на стр. 207 и в разъясняющих примечаниях А. П. Котельникова 26—29. 3Привести здесь эти вычисления, к сожалению, невозможно. Читатель найдет их в мемуаре «О началах геометрии» в томе «Полного собрания сочинений Н. И. Лобачевского», стр. 219-222; к ним даны обстоятельные примечания А. П. Котельникова. В вычислениях Лобачевского оказался недосмотр, который А. П.Котельниковым исправлен. 4Н. Liebmann. N. I. Lobatschefskij. Imaginaire Geometrie. Leipzig, 1904, стр. VII. 5У нас уравнения (11). 6У нас (10). |
загрузка...
