§ 70. Развитие квантовой механики

К созданию матричной механики — одной из форм квантовой механики на первом этапе ее развития — Гейзенберг (1901—1975) пришел в результате исследований спектральных закономерностей, а также теории дисперсии.

Классическая теория дисперсии основывалась на представлении, что вещество состоит из электрических осцилляторов, способных поляризоваться и приходить в колебательное движение под влиянием электромагнитных волн. Пусть собственная частота электрического осциллятора равна ν₀ и на него падает монохроматическая электромагнитная волна E₀^e2πνt. Тогда этот осциллятор, если предположить, что заряд равен заряду электрона, приобретает переменный электрический момент, амплитуда которого без учета затухания равна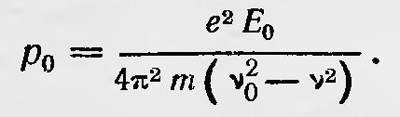

Если в единице объема содержится N осцилляторов, то простой подсчет позволяет определить диэлектрическую проницаемость вещества, а значит, и показатель преломления n. Для прозрачной области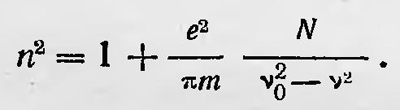

Принимая во внимание, что осцилляторы могут иметь различные собственные частоты ѵ₁, ѵ₂, ..., формулу нужно записать в виде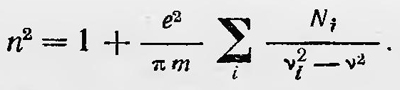

Последняя формула в основном хорошо выражала зависимость показателя преломления от частоты ѵ в области нормальной дисперсии.

Конечно, в классической теории дисперсии оставались неясные моменты. В частности, это вопрос о числе осцилляторов N₁, N₂, ..., которые, как показывали измерения, нельзя было просто отождествить с общим числом электронов в атоме, полагая, что каждый из них является гармоническим осциллятором. Поэтому было введено понятие «дисперсионных электронов», т. е. электронов, участвующих в процессах дисперсии. Появление и развитие теории Бора заставили по-новому взглянуть на процессы поглощения, дисперсии и рассеяния света атомами. По Бору, уже не электрон в атоме является одним из осцилляторов, который при возбуждении совершает колебания с определенной частотой, а каждый из них способен возбуждаться и излучать разные частоты, переходя из возбужденных состояний в невозбужденное. Таким образом, с точки зрения Бора механизм взаимодействия света с веществом, механизм излучения, дисперсии, рассеяния света совсем иной, нежели тот, который представлялся в классической физике.

Как же построить теорию излучения, дисперсии и рассеяния света по Бору? Для решения этой задачи был опять же использован принцип соответствия, т. е. проведена аналогия между классическим и квантовым рассмотрениями взаимодействия света с веществом. Применяя принцип соответствия, нужно классическим осцилляторам (дисперсионным электронам), имеющим собственные частоты колебаний ν₁, ν₂, поставить в соответствие атом как набор осцилляторов с частотами, определяемыми по теории Бора соотношением

ν=(E_m-E_n)/h.

Что же касается числа дисперсионных электронов N₁, N₂, N₃, то всем им нужно сопоставить величины, определяемые вероятностями переходов атома из одного состояния в другое, при котором излучается или поглощается соответствующая частота. Эти вероятности были введены Эйнштейном еще в 1917 г.¹ при выводе закона черного излучения Планка (коэффициенты Эйнштейна).

В этом направлении и развивалась квантовая теория дисперсии, начиная с работы Ладенбурга, относящейся к 1921 г.² Квантовая теория дисперсии приводит к следующей формуле для показателя преломления: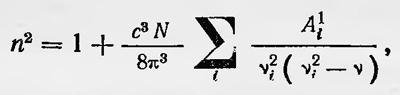

где N — число атомов в единице объема; A_i¹ — коэффициенты Эйнштейна для спонтанного излучения, соответствующего переходу с высшего энергетического уровня на низший уровень 1 с излучением частоты ѵⁱ. Эта формула отличается от классической. Однако если ввести величину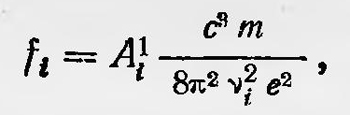

только здесь вместо числа гармонических осцилляторов N_i стоит выражение Nf_i. Это и есть число дисперсионных электронов.

В 1924 г. Крамере указал на то, что в теории дисперсии нужно принять во внимание, что атомы без влияния внешнего электромагнитного излучения могут находиться в возбужденном состоянии, например в состоянии k. Поэтому нужно учитывать переходы в состояние k как из высших состояний і, так и из низших состояний j. В этом случае формула дисперсии принимает вид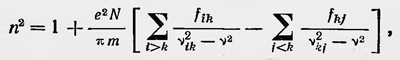

где ν_ik=(E_i-E_k)/h и ν_kj=(E_k—E_j)/h, f_ik и f_kj - соответствующие силы осцилляторов.

Предположения Крамерса оправдались. Через несколько лет было обнаружено явление отрицательной дисперсии при прохождении света через положительный столб газового разряда.

Квантовая теория дисперсии, развитая на основании теории Бора, уже не опиралась на модельные представления о строении атома. Если и можно говорить о модели атома в этой теории, то только лишь как о символической математической модели. В этой модели атом представлялся как совокупность виртуальных гармонических осцилляторов q_ij=a_ije^{2πiν^ljt}, названная Ланде «виртуальным оркестром»³.

Представления же об атоме как о системе, состоящей из ядра и вращающихся вокруг него электронов, которые обладают определенной массой, движутся с определенной скоростью по определенной траектории, нужно понимать лишь как аналогию для установления соответствующей математической модели. При этом особую роль играл принцип соответствия как принцип аналогии между классическим и квантовым рассмотрениями⁴.

Указанный метод исследования развил Гейзенберг в 1926 г., распространив его вообще на теорию атомных явлений. Еще в 1923 г. Гейзенберг принял точку зрения, согласно которой «модельные представления принципиально имеют только символический смысл, они являются классическими аналогами «дискретной» квантовой теории»⁵. Именно таким путем Гейзенберг рассчитывал преодолеть трудности, возникшие перед полуклассической теорией Бора. В работе 1926 г.⁶. Гейзенберг, впервые высказывая основные положения квантовой механики в матричной форме, развил приведенную выше мысль. Теория атомных явлений, по Гейзенбергу, должна ограничиваться установлением соотношений между величинами, которые непосредственно измеряются в экспериментальных исследованиях («наблюдаемыми» величинами, по терминологии Гейзенберга) — частотой излучения спектральных линий, их интенсивностью, поляризацией и т. п. «Ненаблюдаемые» же величины, такие, как координаты электрона, его скорость, траектория, по которой он движется, и т. д., не должны использоваться в теории атома. Однако в согласии с принципом соответствия новая теория должна определенным образом соответствовать классическим теориям. Конкретно это должно выражаться в том, что соотношения новой теории должны находиться в отношении аналогии с соотношениями классических величин. При этом каждой классической величине нужно найти соответствующую ей квантовую величину и, пользуясь классическими соотношениями, составить соответствующие им соотношения между найденными квантовыми величинами. Позднее в своей работе «Физические принципы квантовой теории» Гейзенберг писал:

«Для вывода математической схемы квантовой теории (это относится как к корпускулярному, так и к волновому представлению) мы имеем в распоряжении два источника: эмпирические факты и принцип соответствия. Боровский принцип соответствия в своей наиболее общей формулировке гласит, что между квантовой теорией и соответствующей данной примененной картине классической теории существует качественная аналогия, которая может быть проведена до деталей. Эта аналогия не только дает указания для нахождения формальных законов, ее особенное значение заключается главным образом в том, что она одновременно дает и физическую интерпретацию найденных законов»⁷.

Используя этот принцип, Гейзенберг и строит новую теорию. Одними из самых основных величин, характеризующих состояние частицы в классической механике, являются прежде всего ее координаты как функции времени, например координата x(t). В квантовой механике понятие координаты теряет смысл:

«Электрону,— пишет Гейзенберг,— нельзя сопоставить с помощью наблюдаемых величин некоторую точку пространства, являющуюся функцией времени»⁸.

Вопрос, какую величину, образованную из «наблюдаемых», нужно сопоставить в квантовой механике координате x(t), Гейзенберг решает следующим образом. В классической физике для случая одной степени свободы координату материальной точки, если она совершает периодическое движение, можно представить в виде ряда Фурье: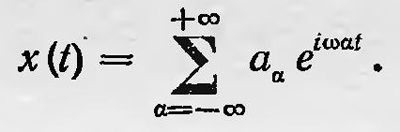

С другой стороны, атом в теории дисперсии представляется как совокупность гармонических осцилляторов:

q_nm=a_nme^iω(n,m)t.

Таким образом, классической координате частицы нужно поставить в соответствие в квантовой механике совокупность величин q_nm=a_nme^iω(n,m)t, где ω(n,m) — одна из возможных частот, излучаемых или поглощаемых частицей при переходе из состояния с энергией Е_n в состояние с энергией Е_m так, что согласно постулату Бора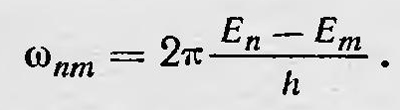

Амплитуда a_nm связана с вероятностью такого перехода, и значение |a_nm| определяет интенсивность излучаемого при этом электромагнитного излучения частоты ω_nm.

Если классической координате x(t) соответствуют в квантовой механике совокупность осцилляторов q_nm=a_nme^iω(n,m)t, то какая же квантовая величина соответствует классической величине х²(t)? Величину x²(t) можно опять-таки представить в виде ряда, воспользовавшись разложением в ряд x(t), а именно: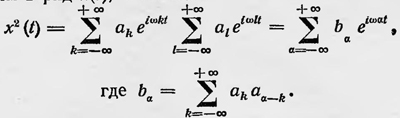

Такое представление х²(t) позволяет Гейзенбергу сопоставить этой величине опять-таки совокупность гармонических осцилляторов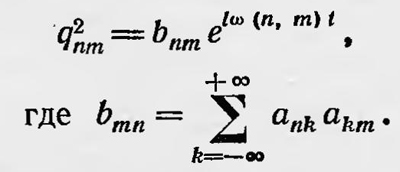

Рассуждая аналогично, можно определить квантовые величины, соответствующие классическим величинам x³(t), x⁴(t), ... и т. д. Следовательно, и для любой функции f[x(t)], допускающей разложение в ряд по степеням х, можно найти квантовые величины — совокупности соответствующих осцилляторов.

Далее можно образовать квантовые аналогии для величин x(t), x(t) и т. д. За квантовый аналог для x(t) принимается совокупность осцилляторов

q_nm= iω(n,m)a_nme^iω(n,m)t и т. д.

Проводя соответствие между квантовым и классическим рассмотрениями атомных явлений, нужно допустить, что между квантовыми величинами существуют соотношения, аналогичные имеющим место между соответствующими классическими величинами. Рассмотрим, например, периодическое движение частицы, имеющей одну степень свободы. В классической физике уравнение движения имеет вид

x + f(x)= 0,

интегрируя которое с учетом начальных значений получаем решение данной задачи.

В квантовой механике этому уравнению нужно сопоставить аналогичное соотношение между квантовыми величинами. При этом f(x) следует разложить в степенной ряд. Но в квантовой механике не имеет смысла говорить о начальных значениях соответствующих величин. Зато в случае периодического движения должно выполняться еще условие квантования

ɸpdq = nh,

где р и q — классические величины (импульс и координата), n — целое число.

Этому полуклассическому, полуквантовому условию нужно найти квантовый аналог. Гейзенберг поступает следующим образом. Для простейшего случая одной степени свободы условие квантования для периодического движения можно записать так:

ɸpdq = ɸmxdx = ɸm(x)² dt = nh.

Воспользовавшись разложением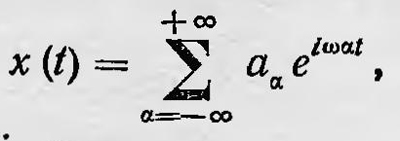

определим x(t), затем [x(t)]² и, наконец, подставим выражение для [x(t)]² в условие квантования и проинтегрируем. В результате получаем условие квантования в преобразованном виде: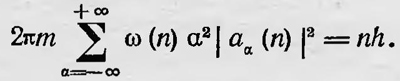

В этом выражении присутствуют только «наблюдаемые» величины. Далее Гейзенберг, пользуясь принципом соответствия, рассматривая а_α(n) и ω(n) как функции n, полагает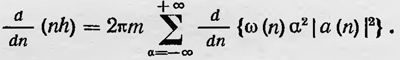

Далее, исходя из ряда соображений, используя теорию дисперсии⁹, Гейзенберг приходит к окончательному выражению для квантового аналога условия квантования: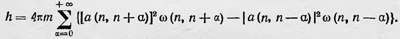

После установления квантового аналога условия квантования Гейзенберг рассмотрел простую задачу ангармонического осциллятора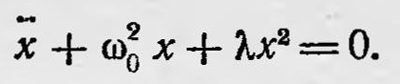

Заменяя в уравнениях движения классические величины х, х², х их квантовыми аналогами и используя квантовый аналог условия квантования, Гейзенберг получил уравнения, позволяющие определить значения ω_nm и а_nm, т. е. излучаемые частоты и их интенсивности.

В том же 1925 г. немецкие физики Борн и Иордан¹⁰ придали идеям Гейзенберга более строгую математическую форму. Они показали, что те величины, которые Гейзенберг поставил в соответствие классическим величинам, язляются матрицами, и с математической точки зрения переход от классической или полуклассической теории к квантовой механике заключается в замене обычных величин и действий над ними матрицами и соответствующими действиями над последними. Основными являются матрица координат q и матрица импульса р с элементами q(n,m)e^2πiν(nm)t и р(n,m)e^2πiν(nm)t. Из этих матриц можно образовать матрицы других физических величин и соответствующих соотношений между матрицами, являющимися аналогами классических соотношений. Так, например, можно составить матрицу, соответствующую энергии или гамильтониану: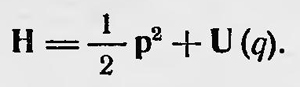

.

Между матрицами справедливы соотношения, соответствующие уравнениям движения, в частности каноническим уравнениям Гамильтона: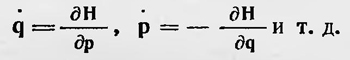

Матрицы, изображающие физические величины, должны быть эрмитовыми, т. е. такими, элементы которых удовлетворяют условию q_nm=q_nm* где знак «✶» означает переход к комплексно-сопряженной величине.

Наконец, Борн и Иордан показали также, как в матричной форме следует записать условие квантования. Это условие, называемое перестановочным соотношением, имеет вид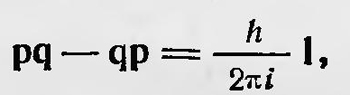

где l — единичная матрица.

В последующей работе совместно с Гейзенбергом Борн и Иордан¹¹ развивают математический аппарат матричной механики, применив его для решения ряда задач.

Независимо от перечисленных выше авторов английский физик Поль Антуан Морис Дирак (1902), познакомившись с теорией Гейзенберга, разработал для новой теории несколько иной математический аппарат¹². Дирак вводит в квантовую механику вместо матриц линейные дифференциальные операторы, первоначально назвав их q-числами¹³. Наиболее интересно применение Дираком квантовых скобок Пуассона. Он показал, что классическим скобкам Пуассона [f₁, f₂] следует сопоставить квантовые скобки Пуассона, а именно: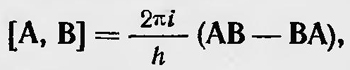

где А и В — операторы, соответствующие классическим величинам f₁ и f₂, которые являются функциями канонических переменных.

Если в качестве функции f₂ взять функцию Н Гамильтона, зависящую от р и q, то скобки Пуассона определяют изменение какой-либо механической величины f(q, р, t) со временем: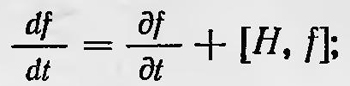

если f — интеграл движения, то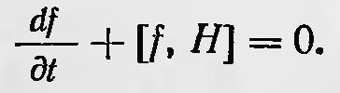

Аналогичное соотношение существует и в квантовой механике. Так, например, можно записать выражение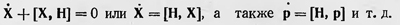

Дирак показал, как, используя квантовые скобки Пуассона, можно получить перестановочные соотношения: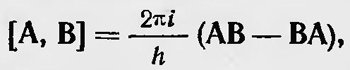

Рассмотрим теперь направление в развитии теории атома, основанное на других принципах, нежели те, на которые опирались Гейзенберг, Борн, Дирак и др. Это направление начало развиваться в работах французского физика Луи де Бройля (1892), первые из которых были опубликованы в 1923 г.¹⁴. В них была высказана идея о волновой природе материальных частиц. Дальнейшее развитие эта идея получила в последующих работах де Бройля и, в частности, в его докторской диссертации, защищенной в Сорбонне в 1924 г.¹⁵

На основании уже установленного факта наличия у света одновременно и корпускулярных и волновых свойств, а также оптико-механической аналогии у де Бройля возникла идея о существовании волновых свойств у частиц. Вспоминая о размышлениях, которые привели его к представлению о «волнах материи», де Бройль писал:

«В оптике пришлось ввести понятие частицы наряду с понятием волны. Казалось, что природа света обладает странной «двойственностью».

Но если в теории света в течение целого столетия слишком пренебрегали понятием «частицы» для того, чтобы пользоваться исключительно понятием «волны», не была ли допущена обратная ошибка в теории материи? Были ли вправе физики пренебрегать понятием «волны» и думать только о понятии «частицы»? Эти вопросы несколько лет тому назад задал себе автор, обдумывая аналогию между принципом наименьшего действия и принципом Ферма и ища смысл таинственных квантовых условий, введенных во внутриатомную динамику Планком, Бором, Вильсоном и Зоммерфельдом»¹⁶.

Луи де Бройль

Основные идеи де Бройля, высказанные им в его работах, сводятся к следующему. Так же как фотон, материальные частицы обладают корпускулярными и волновыми свойствами. Со всякой покоящейся материальной частицей связан периодический процесс с частотой ѵ₀, которая определяется из соотношения Планка hѵ₀= Е, где Е — энергия частицы. С другой стороны, из соотношения Эйнштейна следует, что эта энергия связана с массой уравнением Е = m₀c², где m₀ — масса покоя. Из этих двух выражений получаем

ν₀=1/h m₀c².

Колебательный процесс, связанный с частицей, можно записать также в виде

φ= sin2πѵ₀е₀,

где м₀ и t₀— величины, определяемые в той системе отсчета, где частица покоится.

Если теперь перейти к системе отсчета, которую будем считать неподвижной и в которой частица движется со скоростью ѵ, то, пр именяя формулу преобразования для времени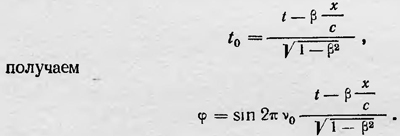

Это выражение описывает распространяющуюся вдоль оси х волну с частотой ν и скоростью u, причем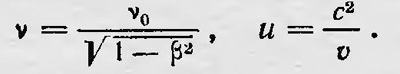

Легко показать, что групповая скорость этой волны равна скорости частицы ѵ.

Для длины волны λ получаем выражение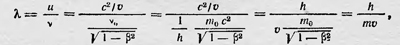

т. e. известное соотношение де Бройля.

Полученные для свободной частицы результаты де Бройль считает возможным распространить и на более общий случай движения частицы с переменной скоростью, т. е. на частицу, находящуюся в силовом поле. Такую возможность он видит в существовании оптикомеханической аналогии, аналогии между принципом Ферма в оптике и принципом Мопертюи в механике.

Запишем выражение для принципа Ферма применительно к фазовой волне: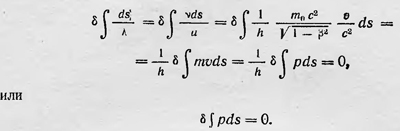

Теория де Бройля объясняет квантовые условия устойчивости круговых орбит, установленные Бором. Движение электрона по круговой орбите устойчиво только тогда, когда длина фазовой волны укладывается целое число раз на окружности, описываемой электроном, т. е. когда nλ = 2πr, где n — целое число. Для данного случая λ=h/(mv) = h/(mωr), и мы получим

nh = 2πmωr², или mωr²=n h/2π

т. е. условие устойчивости орбит Бора. Иначе, орбита устойчива в том случае, когда $ds/X= п, т. е. целому числу. Это условие, если учесть соотношение λ = h/р, установленное де Бройлем, сейчас же переходит в известное квантовое условие.

Введя представление о волнах, связанных с движущейся частицей (они получили название волн де Бройля или волн материи), де Бройль не дает определенного ответа на вопрос, что представляют собой эти волны, какова их природа? Он только подчеркивает, что это не обычные материальные волны, несущие энергию. Это следует из того, что их скорость больше скорости света, следовательно, их распространение не может быть распространением энергии того или иного вида. Де Бройль называет эти волны «фазовыми волнами» и пишет, что

«Я нарочно дал довольно неотчетливые определения фазовой волны и периодического явления, которое она, гак же как и квант снега, некоторым образом выражает. Настоящую теорию нужно, таким образом, рассматривать скорее как форму, физическое содержание которой не вполне установлено, чем как окончательно разработанную стройную теорию»¹⁷.

Эрвин Шредингер

Первые работы де Бройля, в которых высказывалась идея волн, связанных с материальными частицами, не обратили на себя серьезного внимания со стороны большинства физиков-теоретиков. Де Бройль впоследствии писал, что идеи, которые он высказал, были приняты с «удивлением, к которому несомненно примешивалась какая-то доля скептицизма»¹⁸. И действительно, на теоретиков, занимавшихся атомной физикой (Бора, Гейзенберга, Дирака, Борна и др.), они не произвели положительного впечатления. Интерес к идеям де Бройля проявил Эйнштейн, который хотя и назвал диссертацию де Бройля книгой, написанной как будто сумасшедшим, тем не менее она заинтересовала его. В частности, он уже в 1925 г. использовал результаты теории де Бройля в статической физике при построении статистик Бозе—Эйнштейна¹⁹. Особенно сильное влияние идеи де Бройля оказали на австрийского физика Эрвина Шредингера (1887—1961), который увидел в них источник для создания новой атомной механики. В 1926 г. последовали работы Шредингера, в которых он, развивая идеи де Бройля, построил так называемую волновую механику. В первом сообщении²⁰ Шредингера постановка вопроса носит довольно формальный характер. Он хочет заменить непонятные постулаты Бора о дискретных состояниях атома и правила квантования некоторыми положениями, в которых нелочисленность получается естественным образом сама собой подобно тому, как сама по себе получается целочисленность числа узлов при рассмотрении колеблющейся струны. Исходя из уравнения Гамильтона-Якоби H(q, δS/δq)=E, заменяя функцию S через S = kInψ, где k=h/2π, и рассматривая некоторую вариационную задачу, он получает для атома водорода уравнение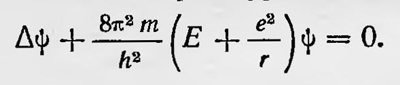

Оказывается, что это уравнение для случая Е < О имеет конечные, непрерывные и равные нулю на бесконечности решения только при определенных значениях Еп = —2л 2meV(hn)2, где п — любое целое положительное число, большее нуля. Таким образом, автоматически получается хорошо известное выражение для энергии дозволенных орбит, найденное Бором на основе выдвинутых им постулатов.

Обсуждая полученные результаты, Шредингер подчеркивает, что пришел к ним под влиянием исследований де Бройля. Он указывает, что функция ψ естественным образом связана с неким колебательным процессом в атоме. Но, прежде чем основываться на конкретном представлении об этом волновом процессе, он решил сначала избрать чисто математический способ, так как он дает возможность лучше выяснить все существенные стороны вопроса. В следующем сообщении²¹ Шредингер уже не ограничивается формальной постановкой вопроса, а приводит рассуждения, оправдывающие полученное им уравнение. При этом он исходит из оптико-механической аналогии Гамильтона.

В классической механике задача движения механической системы сводится к решению уравнения Гамильтона—Якоби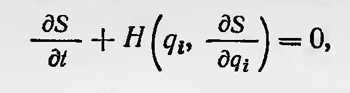

где 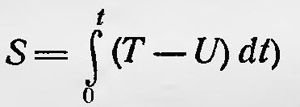— действие, которое является функцией координат и времени.

Если система консервативна, то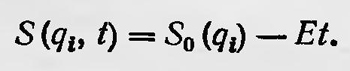

Тогда, подставив выражение для S в уравнение Гамильтона—Якоби, получим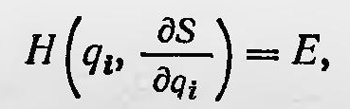

учитывая выражение для гамильтониана Н, можно это выражение записать в виде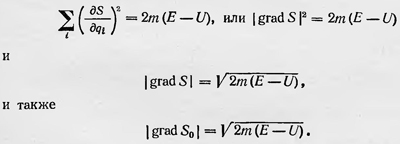

Полученному результату можно дать простую геометрическую интерпретацию. Уравнение S = S₀(q_i)—Et = const можно рассматривать как уравнение, описывающее семейство поверхностей в конфигурационном пространстве q_i так что каждому значению t соответствует своя определенная поверхность S₀(q_i) = Et. Для каждой поверхности в каждой точке можно построить нормаль n. При этом, по определению градиента,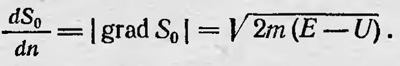

Но вместо того чтобы рассматривать семейство поверхностей для различных моментов t, можно положить, что все эти поверхности являются одной и той же поверхностью в разные моменты времени, т. е. рассматривать эту поверхность распространяющейся в пространстве (q_i).

Очевидно, что скорость распространения поверхности u=dn/dt. Учитывая, что S(q_i,t) = S₀(q_i) — Et = const, имеем dS₀(q_i) = Edt и для скорости распространения поверхности S₀(q_i) получим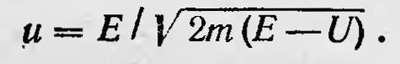

Таким образом, получена картина, аналогичная картине распространения волн, причем S(q, t) поверхность фазы, а скорость распространения поверхности равного действия равна фазовой скорости. Однако эта аналогия, известная уже Гамильтону, не полная. Она справедлива, если ограничиться только геометрической оптикой, которая является лишь приближением к волновой или физической оптике, Такие основные понятия волновой оптики, как уравнение распространения волн, длина волны, частота колебания и т. д., совсем не используются в данной аналогии. Но возможно, что обычная механика также является приближенной, справедливой только для обычных макропроцессов, и должна быть заменена для микропроцессов более точной механикой. Во всяком случае, такое предположение возникает, если обратиться к атомным явлениям. В этом случае, распространяя оптикомеханическую аналогию и опираясь на идеи де Бройля, можно предположить, что механика для микропроцессов должна иметь волновой характер.

«Быть может, наша классическая механика,— пишет Шредингер,— представляет полную аналогию с геометрической оптикой и подобно последней отказывается служить и не согласуется с действительным положением вещей при размерах и радиусе кривизны траекторий, приближающихся по величине к некоторой длине волны, которая теперь принимает в q-пространстве реальный смысл»²².

Продолжая рассуждать таким образом, Шредингер приходит к мысли, что механические процессы следует понимать или изображать как некие волновые процессы, характеризуемые волновой функцией ψ. Тогда образ материальной точки, занимающей, например, определенное место в пространстве, строго говоря, является приближенным и может быть сохранен только при рассмотрении макропроцессов, подобно току, как мы пользуемся представлением о световом луче, которое теряет смысл, если рассматривать явления дифракции и интерференции.

Функция ψ должна удовлетворять волновому уравнению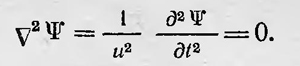

Полагая, как обычно, что Ψ=ψ(q_i)e^2πiνt , и подставляя Ψ в волновое уравнение, имеем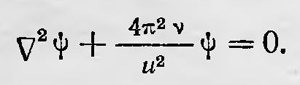

Учитывая далее, что ν= E/h и 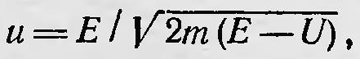, это уравнение можно записать в виде

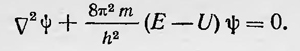
Таким образом, получено уже известное из предыдущей статьи волновое уравнение Шредингера в общем виде. Шредингер ставит вопрос о связи его теории с теорией Гейзенберга, Борна и Иордана. Он высказывает мысль, что, несмотря на то что обе теории основываются на совершенно различных принципах, тем не менее между ними должно существовать связующее звено.

«Я совершенно уверен в том, что обе эти попытки,— пишет Шредингер,— не только не будут противоречить друг другу, но даже, наоборот, вследствие полного различия исходных положений и методов окажутся взаимно дополняющими. Сила гейзенберговской программы заключается в том, что она обещает вычислять интенсивности линий, в то время как мы к этому вопросу пока совершенно не подходили. Сила же представленного в данной работе метода заключается, как я могу судить, в использовании руководящего физического представления... Мне лично особенно нравится приведенное в конце предыдущей статьи истолкование излучаемых частот как «биений», причем я думаю, что таким образом будет получено также наглядное истолкование формул для интенсивности»²³.

В том же году в работе «О соотношении квантовой механики Гейзенберга, Борна, Иордана и моей»²⁴ Шредингер впервые установил связь между квантовой и волновой механикой, которую уточнил в последующих работах. Он показал, что при всем различии исходных физических положений они математически эквивалентны. Основные идеи Шредингера в данном исследовании (в уточненном впоследствии виде) заключаются в следующем. Связующее звено между матричной и волновой механикой Шредингер видит в понятии линейного дифференциального оператора. Именно физической величине, являющейся функцией q и р, нужно сопоставить определенный оператор F.

Пусть имеется полная ортогональная система волновых функций ψ₁(q), ψ₂(q), ψ₃(q), ..., являющихся решением волнового уравнения для какой-нибудь физической задачи, которая нормирована, т. е. выполняется условие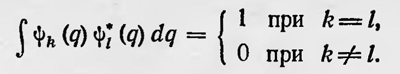

Пусть, далее, каждой из функций соответствует собственное значение, определяемое параметром, которым является энергия системы, т. е. Е₁, E₂, ₃, ... . Образуем теперь с помощью волновых функций и какого-либо оператора F матрицу с элементами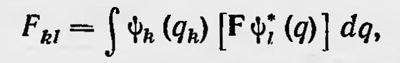

где [Fψ_l(q) — функция координат, получаемая при действии оператора F на функцию ψ_l.

Положим, что оператор умножения на q соответствует координате q: тогда соответствующая матрица имеет элементы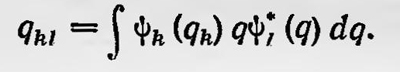

Определив оператор для координаты q, можно аналогично определить и операторы для q², q³ и т.д.

Для того чтобы определить вид оператора и соответствующей матрицы для импульса р, используем перестановочное соотношение. Рассмотрим оператор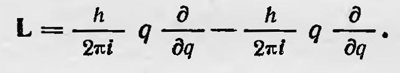

Легко видеть, что действие этого оператора на какую-либо функцию координат ψ(q) сводится к умножению ее на —h/2πi, т. е.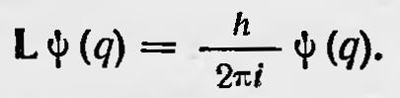

Отсюда элементы матрицы, соответствующие оператору L, таковы: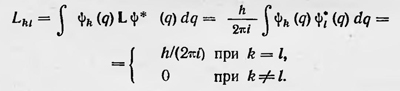

Но элементы матрицы pq — qp = h/2πi 1, выражающей перестановочное соотношение, равны тем же величинам, только взятым с обратным знаком. Поэтому, учитывая, что оператором для координаты q является просто оператор умножения на q, приходим к заключению, что оператор, соответствующий импульсу р, должен иметь вид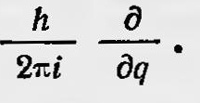

При этом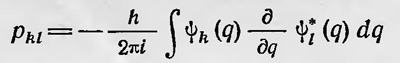

— элемент соответствующей матрицы.

Теперь можно образовать операторы и соответствующие матрицы, которые представляют разные физические величины, выражающиеся в виде определенных функций q и р. Особое значение при этом имеет оператор Гамильтона или в данном случае оператор энергии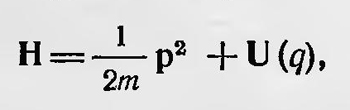

который, согласно определению оператора для р, имеет вид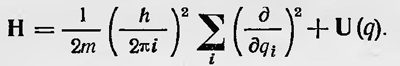

Действие этого оператора на какую-либо из собственных функций ψ_h(q) должно сводиться к умножению ее на собственное значение энергий E_k. Это сразу следует из уравнения Шредингера, которое можно записать в виде

Нψ=Еψ.

Так как это уравнение удовлетворяется любой из функций ψ_k(q) то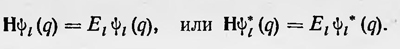

Умножая последнее уравнение на какую-либо другую функцию ψ_k(q) и интегрируя, получаем выражение для элемента матрицы энергии: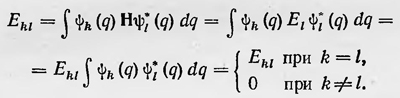

Таким образом, матрица энергии должна быть диагональной матрицей, и ее диагональные элементы, отличные от нуля, равны значениям энергии E_kk или просто _k.

Как показал Шредингер, все матрицы, образованные с помощью собственных функций ψ₁(q), ψ₂(q),..., являющиеся решением волнового уравнения и соответствующие определенным операторам, применяются р матричной механике и представляют собой матрицы Гейзенберга.

Правда, элементы матриц Гейзенберга имеют множитель e^iωkl^t или eⁱ2π/h^(E_k-E_l). Однако если вспомнить, что и в теории Шредингера, вообще говоря, волновая функция для стационарного состояния с определенной энергией E_k должна иметь вид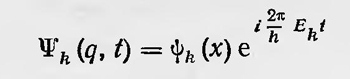

и, следовательно, нужно, вообще говоря, при образовании соответствующих матриц использовать функцию Ψ_k(q,t), а не ψ_k(q), то мы и получим матрицы, имеющие множитель е^t2π/h (^E_k-E_l). Так, например, элемент матрицы, соответствующей координате, равен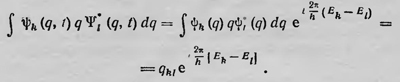

To же самое и для других матриц. Эти матрицы уже полностью совпадают с матрицами Гейзенберга.

Таким образом, все матрицы Гейзенберга, рассматриваемые в матричной механике, получаемые с помощью соответствующего формализма, вычисление которых являлось задачей этой механики, Шредингер получает, решая волновое уравнение. Отсюда следует, что с математической точки зрения матричная и волновая механики эквивалентны.

Теперь, для того чтобы решить вопрос об интенсивностях частот, излучаемых квантовой системой, следовало воспользоваться тем, что этот вопрос в матричной механике уже был решен. Так, например, интенсивность какой-либо из спектральных линий определенной частоты, излучаемой атомом водорода, определялась амплитудой элемента матрицы, соответствующей электрическому моменту электрона в этом атоме. Так, собственно говоря, и поступил Шредингер. Однако он дал свою физическую интерпретацию процесса излучения, основанную на представлении о волновой функции. Электрон, по мнению Шредингера, не является частицей, а представляет собой электрический заряд, размазанный в пространстве. При этом плотность заряда определяется волновой функцией так, что |ψ|² или ψψ* равно плотности заряда. С этой точки зрения атом водорода представляет собой ядро, окруженное облаком отрицательного заряда, и если атом находится в стационарном состоянии, то плотность заряда ψψ* не зависит от времени и остается постоянной. Если же атом находится в состоянии, которое описывается более сложной волновой функцией, то плотность заряда меняется и атом излучает

В общем случае волновую функцию электрона в атоме водорода можно записать в виде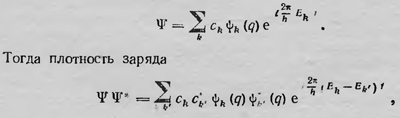

т. е. плотность заряда не остается постоянной, а осциллирует с частотами ν_kk=2π/h (E_k-E_l), которые совпадают с боровскими частотами. Для того чтобы найти интенсивность излучения, нужно определить изменение со временем электрического момента атома М, например в направлении осп х. Возьмем простой случай, когда состояние атома характеризуется функцией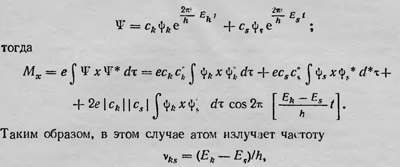

амплитуда которой определяется величиной 2е|c_k||c_S|∫ψ_kxψ_Sτ, пропорциональной соответствующей матрице Гейзенберга.

Интерпретация волновой функции показалась Шредингеру удачной. Во-первых, она была наглядной (в отличие от представлений матричной механики, которые носили формальный символический характер). Во-вторых, теория Шредингера, как он предполагал, возвращала к представлению о непрерывности процессов, происходящих в физике. Говоря о том, как можно себе представить механизм излучения атомом света с помощью вышеприведенных соображений, Шредингер в том же 1926 г. писал Лоренцу:

«Я сразу настолько обрадовался тому, чго удалось получить картину, где хоть что-то имеет действительное отношение к тем частотам которые мы наблюдаем в излучаемом свете, что я с бьющимся сердцем затравленного беглеца набросился на это что-то в том виде, в котором оно представилось непосредственно, именно на амплитуды, изменяющиеся периодически с частотой биений Этим я хотел лишь сказать, что мыслим такой механизм посредством которого эти изменяющиеся амплитуды возбуждают свет той же частоты Наобороі дис кретные частоты воровской модели казались мне, и сейчас кажутся (уже с 1914 і ) чем-то столь чудовищным, что я охарактеризовал бы возбуждение света іиким путем, как немыслимое»²⁵.

Однако, как ни заманчива была такая интерпретация, она встретила целый ряд трудностей. Во-первых, чтобы атом излучал, он должен был находиться сразу в нескольких, по крайней мере двух, состояниях Следовательно, возможность спонтанного излучения атома, находя щегося в возбужденном стационарном состоянии, исключалась, противоречило ранее существовавшим взглядам. Во-вторых, указанное простое толкование волновой функции допустимо только для ашма водорода, который обладает одним электроном Для многоэлектронных атомов ψψ* уже нельзя было рассматривать как плотность электрического заряда, распределенного в пространстве, поскольку в этом случае ψ — функция координат всех электронов и, если и можно говорить о величине ψψ* как о плотности электрического заряда, то только в конфигурационном пространстве Зn-измерений, где n — число электронов в атоме. Но в этом случае волновая функция уже теряет свой наглядный смысл.

Наконец, как интерпретировать с точки зрения волновой функции существование электрона как частицы? Для решения этого вопроса Шредингер обратился к представлению о волновом пакете. Он высказал сначала мысль, что электрон в тех случаях, когда он проявляет себя как частица, является определенной группой волн де Бройля, так называемым волновым пакетом. Однако, несмотря на то что он уделил этому вопросу достаточное внимание, провести эту точку зрения ему не удалось. Расчеты показали, что, исключая частный случай осциллятора, не удается образовать такую группу волн (волновой пакет) из волн де Бройля, которая бы достаточно долго могла сохранять свои размеры в пространстве, двигаясь как целое. Хотя в начальный момент времени из волн де Бройля и можно было составить такой волновой пакет, что ψψ* практически отличалось от нуля лишь в малой области пространства и он мог быть интерпретирован как частица, тем не менее в общем случае довольно быстро эта группа волн будет расползаться по всему пространству и ее уже нельзя интерпретировать как частицу.

Все эти вопросы сразу же встали перед Шредингером. Он старался их решить, продолжая работать над дальнейшим построением теории. Прежде всего, разрабатывая вопрос излучения атома, он обобщил волновое уравнение на случай, когда волновая функция зависит от времени, а затем рассмотрел вопрос дисперсии. До сих пор Шредингер рассматривал задачу о стационарных состояниях атома, представляющего консервативную систему. Для решения этой задачи он установил уравнение, которое не содержал о времени. Для решения же более общей задачи, например задачи об атоме, находящемся в переменном электромагнитном поле, нужно было установить более общее волновое уравнение, содержащее время. Для нахождения такого уравнения можно было бы воспользоваться аналогией с оптикой, полагая, что уравнению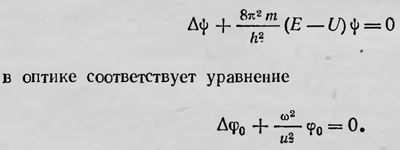

Полное же уравнение волновой механики должно соответствовать полному волновому уравнению в оптике: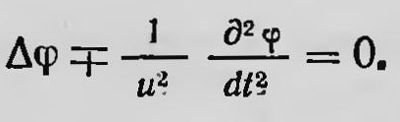

Учитывая, что скорость распространения волн де Бройля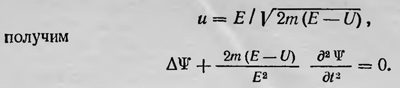

Однако это уравнение не подходит, так как содержит Е — энергию, которая в волновой механике имеет смысл частотного параметра и поэтому в полное уравнение не должна входить.

Шредингер поступает иначе. Он берет выражение для Ψ в виде

д

и является полным уравнением волновой механики по Шредингеру.

Шредингер применяет это уравнение при рассмотрении задачи о дисперсии. При этом он использует математический аппарат теории возмущений, полагая, что атом находится во внешнем электрическом поле, которое мало по сравнению с внутриатомным электрическим полем, а также что внешнее электрическое поле создается плоской монохроматической волной, длина которой велика по сравнению с размерами атома. В этом случае потенциальную энергию электрона в атоме можно записать в виде

U = U₀ + V,

где U₀ — потенциальная энергия электрона в отсутствие возмущения, а V = exE₀cosωt. Здесь е — заряд электрона, Е₀ — амплитуда возмущающего поля, x — координата, в направлении которой на электрон действует сила со стороны плоской волны. Уравнение Шредингера для данного случая имеет вид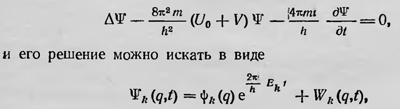

где ψ_k — собственная функция в отсутствие возмущения. Шредингер нашел выражение для Ψ_k(q, t), а затем значение электрическою момента М_x в направлении оси х. Зная М_x, можно найти показатель преломления n. При этом для п получается выражение, идентичное формуле Ладенбурга — Крамерса, о которой мы выше говорили.

Далее, |Ψ(q,t)|² (или ΨΨ*) испытывает периодические изменения с частотой, равной частоте падающего на атом возмущения в направлении оси x. Согласно Шреденгеру, это означает, что плотность электрического заряда в каждой точке пространства осциллирует с этой частотой.

Успехи теории Шредингера сделали эту теорию весьма популярной. С одной стороны, с точки зрения математического формализма она была более удобна, нежели матричная механика. С другой стороны, казалось, во всяком случае сначала, что она дает возможность интерпретировать с понятной точки зрения закономерности атомной физики (без непонятных квантовых скачков, без отказа от наглядных представлений и т. д.).

Борн в своих воспоминаниях писал:

«Волновая механика завоевала намного большую популярность, чем геттингенский и кембриджский варианты квантовой механики»²⁶.

т. е. теория, разработанная Гейзенбергом и др., а также Дираком в Англии. Однако многие теоретики и прежде всего Бор и основоположник матричной механики Гейзенберг, а также Дирак, возражали против шредингеровскон интерпретации волновой функции.

В 1926 г. Шредингер был пршлашен в Копенгаген, где при участии Бора развернулась жаркая полемика вокруг шредингеровской интерпретации квантовой механики. Бор очень настойчиво пытался убедить Шредингера в полной невозможности такой интерпретации, оставаясь на принципах классической физики. Однако Шредингер не сдавался.

«Я помню споры с Бором,— писал Гейзенберг,— которые продолжались допоздна и заканчивались чуть ли не полным отчаянием»²⁷.

«Если бы я мог предположить,— заметил как-то Шредингер с горечью,— что волновая теория будет принята столь серьезно и вызовет такую дискуссию, я бы ее никогда не выдвигал»²⁸.

Но если не принимать шредингеровскую интерпретацию волновой функцни, то что следует понимать под этой функцией, какой физический смысл нужно придать величине Ψ, — на этот вопрос по-новому ответил Борн в том же 1926 г., предложив вероятностное толкование этой функции²⁹. По мнению Борна, волновая функция не представляет собой никакого реального физического поля, а имеет вероятностный смысл, подобно функции распределения, применяемой в статистической физике. К этой идее Борн пришел под влиянием замечания Эйнштейна о том, что двойственная природа света может быть просто понята,если принять, что амплитуда световых волн, а значит, и плотность энергии определяются средней плотностью фотонов в данной течке пространства. С этой точки зрения можно было считать, что физической реальностью в световом луче обладают фотоны, тогда как электромагнитное поле является фиктивным, «призрачным» (Gespensterfeld) или «управляющим» (Fuhrungsfeld) полем. Распространяя эту идею на квантовую механику, Борн и предположил, что функция Ψ также может иметь толы:о статистический, вероятностный смысл, заключающийся в том, что ψψ* определяет плотность вероятности пребывания частицы в данной точке пространства. Основание для такого понимания функции Ψ Борн видел в анализе процесса рассеяния частиц силовым центром. С классической точки зрения эта задача рассматривалась так: на силовой центр падает в направлении, например, оси x поток частиц, который рассеивается этим центром; следует определить относительное число частиц, рассеянных под определенным углом к первоначальному направлению их движения. В волновой механике эту задачу нужно рассматривать с несколько иной точки зрения. В данном случае можно считать, что все падающие частицы не взаимодействуют друг с другом, поэтому нужно искать волновую функцию одной падающей частицы. Такую волновую функцию можно представить как сумму падающей плоской волны и волны, расходящейся от силового центра, т. е.

ψ=u(z)+φ(r).

Эта волновая функция должна удовлетворять уравнению Шредингера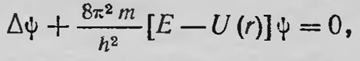

где U(r) — потенциальная энергия частицы в папе данного силового центра; Е — полная энергия частицы, которая в отличие от энергии электрона в атоме водорода должна быть положительной. Полагая, что эта волновая функция является решением данного уравнения Шредингера, Борн нашел ее асимптотическое выражение для r→∞. Если теперь определить выражение |ψ(r)/u(z)|² как функцию угла рассеяния, то получим аналогичное выражение, которое дает теория Розерфорда для отношения числа α-частиц, отклоненных на определенный угол, к числу частиц, прошедших без отклонения при рассеивании их силовым центром. Естественно теперь было принять, что |ψ²| означает плотность вероятности пребывания частицы в данной точке пространства.

Статистическая интерпретация волновой функции, предложенная Борном, получила вскоре широкое признание и стала в основном общепринятой Но теперь возник вопрос о природе статистичности квантовой механики, вокруг которого развернулась впоследствии дискуссия (на ней мы остановимся ниже). Сейчас же кратко упомянем о дальнейшем развитии квантовой механики.

Прежде всего следует отметить, что весьма быстро после первых работ Гейзенберга, Борна и Иордана, Дирака и Шредингера был разработан современный математический аппарат нерелятивистской квантовой механики. Появился целый ряд монографий, посвященных основам квантовой механики, в которых в систематической форме излагался ее математический аппарат, основанный на представлении физических величин в виде операторов (с применением так называемой теории представлений) и т. д.³⁰

В 1927 г. волновая механика получила новое прямое экспериментальное подтверждение. В этом году Дэвиссоном и Джермером было обнаружено явление дифракции электронов. Еще в 1921 г. Рамзауер заметил, что при рассеянии электронов в газах наблюдается отклонение от результатов, предсказываемых классической теорией рассеяния частиц силовым центром. Дэвиссоном и Куисменом в 1923 г. было отмечено, что при рассеянии электронов на поверхности металла кривая рассеяния электронов по углам иногда имеет несколько более или менее выраженных максимумов, что не соответствовало теории. В 1925 г., после работ де Бройля, Эльзассер высказал мысль, что наблюдаемая аномалия является результатом волновой природы электрона и подтверждает гипотезу де Бройля. Однако к этой идее многие отнеслись прохладно, в том числе и сам Дэвиссон.

В 1927 г. Дэвиссон совместно с Джермером производили новые опыты по рассеянию электронов на поверхности металлов Для исправления случайной поломки им пришлось сильно прокалить установку. Произошла перекристаллизация, и вместо множества мелких кристаллов металла, от поверхности которых наблюдалось рассеяние электронов, образовалось несколько больших, и картина распределения рассеянных электронов по углам изменилась. Теперь уже не могло быть Сомнений, что наблюдается явление дифракции электронов от кристаллической решетки, подобно дифракции рентгеновских лучей.

Вскоре явление дифракции электронов было обнаружено и исследовано рядом других физиков. Таким образом, гипотеза де Бройля получила прямое экспериментальное подтверждение, оказалось правильным и найденное им количественное соотношение для длин волн де Бройля. Кроме оправдания квантовой механики непосредственным подтверждением волновой природы электрона с помощью этой теории удалось построить более совершенную теорию твердого тела, теорию электропроводности, термоэлектрических явлений, теорию магнетизма и т. д. Квантовая теория дала возможность приступить к построению теории радиоактивного распада, а в дальнейшем стала основой для новой области физики — ядерной физики и т. д.

Вслед за основополагающими работами Шредингера по волновой механике были сделаны первые попытки релятивистского обобщения квантовомеханических закономерностей, и уже в 1928 г. Дирак заложил основы релятивистской квантовой механики. Однако рассмотрение этого вопроса выходит за рамки настоящей книги.

¹Эйнштейн А. Собрание научных трудов. Т. III, с. 393.
²Zeitschr. f. Phys., 4, 1921, S. 451.
³Naturwiss, 14, 1926, S. 455.
⁴Такой метод исследования был назван Борном в 1924 г. квантовомеханическим (Zeitschr. f. Phys., 26, 1924, S. 379).
⁵Гейзенберг В. Воспоминания об эпохе развития квантовой механики.— В кн.: Теоретическая физика XX века, с. 54.
⁶Heisenberg W. Zeitschr. f. Phys., В. 33, 1925, S. 879.
⁷Гейзенберг В. Физические принципы квантовой теории. М.—Л., Гостехиздат, 1932, с. 80.
⁸Zeitschr. f. Phys. В. 33, 1925, S. 881.
⁹Гейзенберг использует так называемую георему о суммах, доказанную в теории дисперсии Томасом и Куном. По этой теореме, где f_nm н f_mn —силы осциллятора. Если заменить fnm и fmn их выражениями через частоты и амплитуды «дисперсионных электронов» или «виртуальных осцилляторов», то после преобразования можио получить соотношение Гейзенберга.
¹⁰Zeitschr. f. Phys., В. 34, 1925, S. 858.
¹¹Born М., Heisenberg W., Jordan P. Zeitschr. f. Phys., B. 35 1926 S 557
¹²Dirас P. A. M. Proc. Roy. soc. (A). Vol. 109, 1925, p. 642; Vol. 110,1926, p. 561.
¹³Необходимость введения операторов в квантовую механику подчеркивал Н. Винер в 1926 г. (Wіеnеr N. Zeitschr. f. Phys., 36, 1926, S. 174).
¹⁴С. r. Acad. Sei. Vol. 177, 1923, pp. 517, 548, 630. См. также перевод этих работ в УФН, 93, 1927, с. 178, 180, 182.
¹⁵См. список работ де Бройля в кн. Луи де Бройль. По тропам науки. М., ИЛ, 1962, с. 371.
¹⁶Луи де Бройль. Введение в волновую механику. Киев, Гос. научи, техн. изд-во Украины, 1934, с. 8.
¹⁷Л. де Бройль. Исследование по теории кнант.— В кн. Вариационные принципы механики, с. 667.
¹⁸Л. де Бройль. Останется ли квантовая физика индетерминистической?— В кн.: Вопросы причинности в квантовой механике. М., ИЛ, 1955, с. 17.
¹⁹Эйнштейн А. Собрание научных трудов. Т. III, с. 496.
²⁰Шредингер Э. Избранные труды по квантовой механике. М., «Наука», 1976, с. 9.
²¹Шредингер Э. Избранные труды по квантовой механике, с. 21
²²Шредингер Э. Избранные труды по квантовой механике, с. 26—27.
²³Шредингер Э. Избранные труды по квантовой механике, c. 39.
²⁴Там же, с. 56. [Одновременно со Шредингером эту задачу решил Эккерт (Phys. Rev., 28, 1926, p. 711).]
²⁵Шредингер Э. Новые пути в физике.— Статьи и речи. М., «Наука». 1971, с. 208.
²⁶Борн М. Физика в жизни моего поколения. М., ИЛ, 1963, с. 307—308.
²⁷Мур Р. Нильс Бор — человек и ученый. М., «Мир», 1969, с. 184.
²⁸Там же, с. 183.
²⁹Воrn М. Zeitschr. f. Phys., В. 38, 1926, S. 803.
³⁰В качестве первых обобщенных работ по квантовой механике можно назвать следующие: Sommerfeld А Atombau und Spektrallinien, Wellenmechamscher Ergän/ungsband. Braunschweig, 1929 (Зоммерфельд A. Волновая механика. M.—Л., ГТТИ, 1933); Heisenberg W. Die physikalischen Principien der Quantentheorie. Leipzig, 1930 (Гейзенберг В. Физические принципы квантовой теории. М.—Л., ГТТИ, 1932); Dіrас Р. А М. The principles of quantum mechanics. Oxford, 1930 (Диpак П. А. М. Основы квантовой механики. Л.—М., ГТТИ, 1932), и др.